
신윤종 지음
Contents
- Reasoning over Knowledge Graphs
- Path Queries
- Conjunctive queries
- Query2Box
Reasoning over Knowledge Graphs
Knowledge Graphs
- Knowledge 즉, 지식을 그래프의 형태로 구성한 것
- node = entity (labeled with type)
- edge = relationship
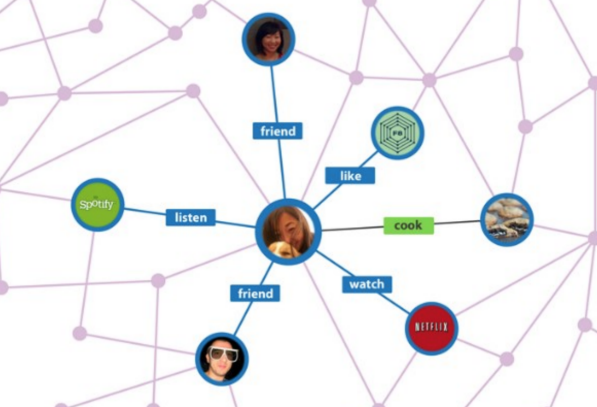
KG Representation
- KG에서의 edge는 triples(h, r, t)로 임베딩 할 수 있다
- head(h): 출발노드(앵커 노드)
- relation(r): edge, 관계
- tail(t): 도착 노드
- 우리의 KG를 임의의 차원으로 임베딩 시키고 실제로 연결되어있는 true triple(h, r, t)가 주어졌다고 해보자
- Ex) h(기생충)의 r(감독) t(봉준호)
- Q1) 기생충의 감독은 봉준호. 즉, h에서 r만큼 이동한 위치가 t의 위치와 똑같아야 겠지?
- Q2) 그러면 (h, r)을 어떻게 임베딩 시킬까?
- Q3) 두 노드 간의 거리는 뭘로 정의하지?
Relation Patterns
Relation의 특성 3가지를 살펴보자

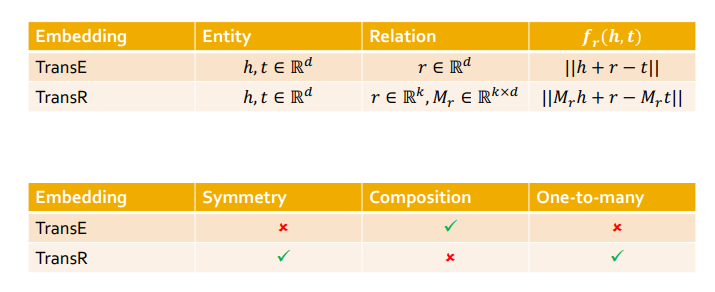
TransE
앞서 Graph representation에서 배웠던 TransE를 써먹을 수 있을 것 같다.
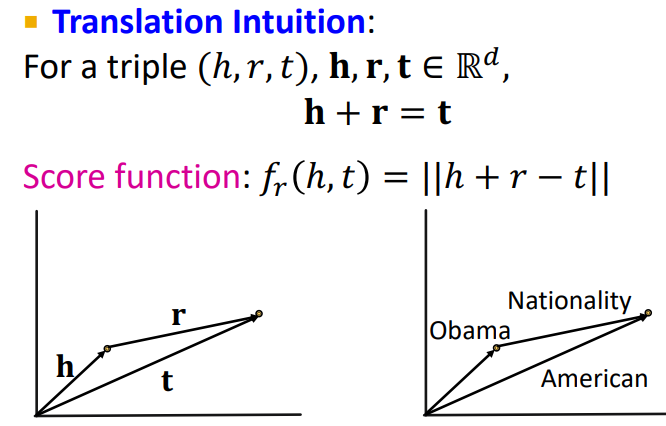
- TransE는 h, r, t를 임의의 차원에 매핑하는 임베딩 방법이다.
- h에서 r만큼 이동한 위치가 t의 위치가 같을 수록 좋다!
TransE Training
TransE는 어떻게 학습할까?

1. True triple과 Corrputed triple(가짜) 2가지를 뽑고 2가지 값과 임의의 마진값의 합을 maximize한다
- True tiple의 거리가 가까울 수록 좋다
- Corrupted tirple의 거리가 멀 수록 좋다
Link Prediction using TransE
- TransE는 Link prediction에 써먹을 수 있다
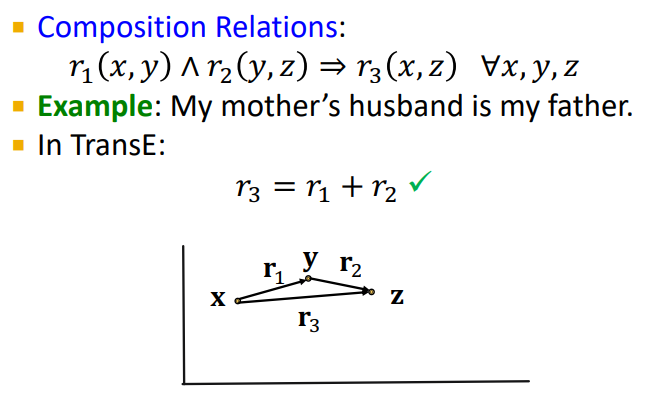
Composition in TransE
- KG의 특성인 Composition을 만족한다
Limitations
- 그러나 TransE는 2가지의 KG 특성을 만족시키지 못한다.
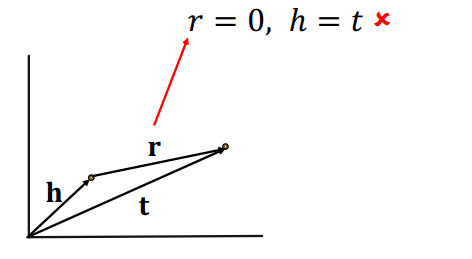
Symmetric relations
- 만약 r이 0이라면 symmetric 특성에 따라 h와 t가 같아야하지만, 실제로 매핑된 TransE값을 보면 h와 t는 서로 다른 벡터이다
N-ary relations
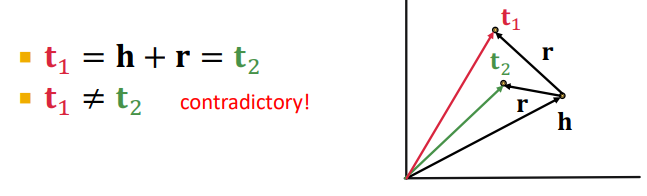
- 일대다, 다대일, 다대다 관계를 만들 수 없다
- 만약 (h, r)의 결과인 t가 많은 경우
- t1 = h+r
- t2 = h+r -> t1과 t2는 같아야한다
- 그러나 t1 != t2
TransR
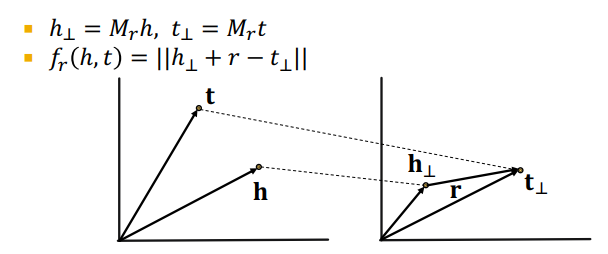
- TransE와 동일하게 entity vector를 임의의 d차원을 매핑한 후 각 relation을 vector r로써 다른 k차원에 매핑한다.
- 임베딩 매트릭스 의 shpae은 (k, d)
Symmetric relation in TransR
- TransR은 symmetric 특성을 보존할 수 있다
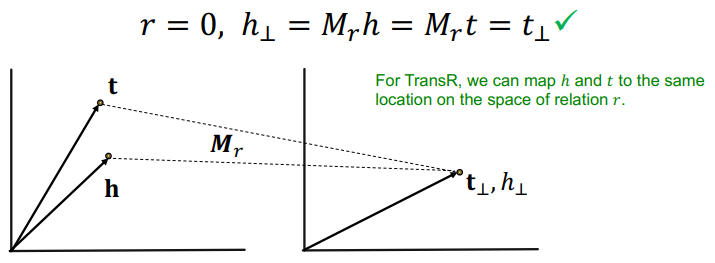
N-ary relation in TransR
- 일대다, 다대일, 다대다 관계도 지킬 수 있다
- d차원에서 다른 노드더라도 r을 통해 k차원으로 매핑시킨다면 같은 값으로 임베딩 될 수 있다
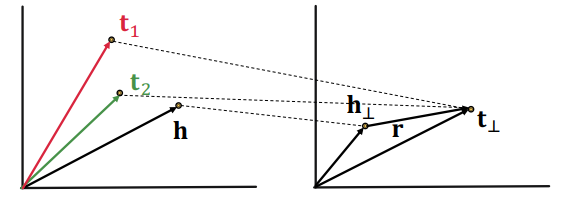
Limitation
- 그러나 TransE와 반대로 composition 관계를 보전할 수 없다
- 왜냐하면 TransR에서 모든 r은 각자 다른 space에 매핑하는 역할이기 때문!
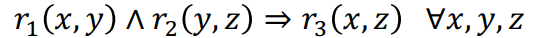
Translation-Based Embedding
Path Queries
Query type on KG
- 만약 multi-hop reasoing을 진행한다면 어떻게 될까?
- 복잡한 질의를 불완전하고 거대한 KG가 다룰 수 있을까?

One-hop queries
- 간단한 one-hop 질의는 link prediction으로 생각할 수 있다
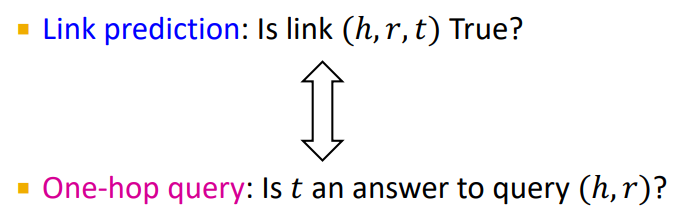
Path queries
- one-hop을 일반화하여 여러 단계로 나누어 path를 구성하여 질의를 진행할 수 있다

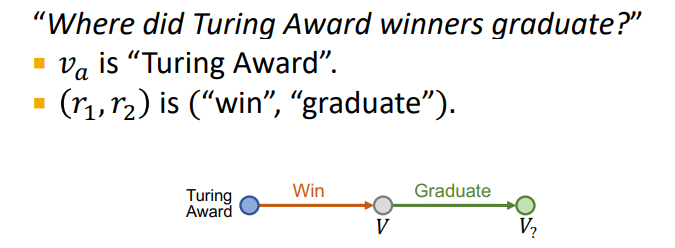
Traversing KG
-
KG에서 multi-hop을 진행해본다고 해보자
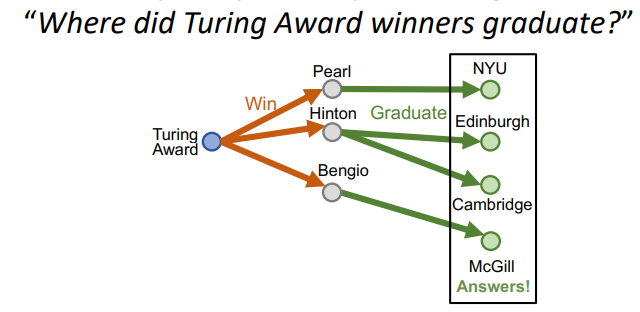
-
IDEA 1) one-hop처럼 link prediction으로 KG를 횡단할 수 있지 않을까?
- NO! KG는 dense graph이기 때문에 매 스텝마다 모든 노드와의 link 확률을 구한다면 시간복잡도는 path의 길이가 n이라면 이 걸린다!
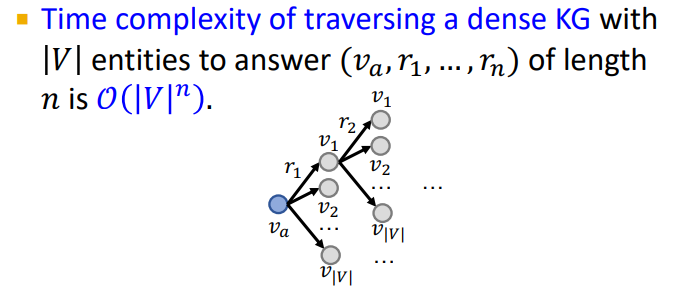
- NO! KG는 dense graph이기 때문에 매 스텝마다 모든 노드와의 link 확률을 구한다면 시간복잡도는 path의 길이가 n이라면 이 걸린다!
-
IDEA 2) query를 임베딩하자
-
TransE를 multi-hop reasoning에 사용할 수 있을 것 같다 -> Compoistion을 만족하니까!
-
score function은 ||q - v||로 바로 구할 수 있으니까 훨씬 빠르다
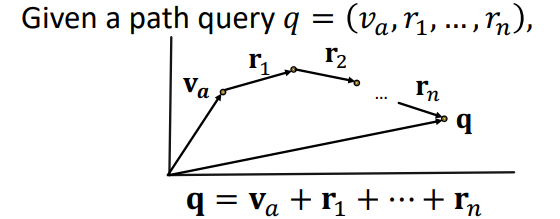
Traversing KG in vector space
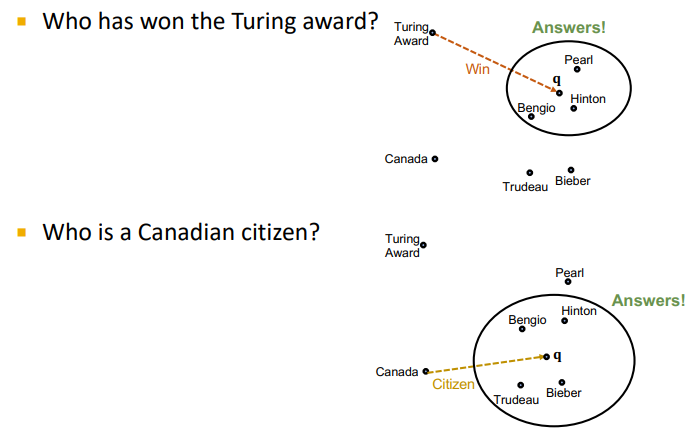
- TransE를 활용한 multi-hop 예시를 보자
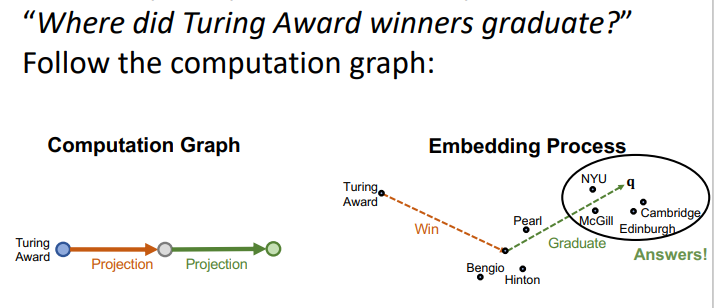
Conjunctive queries
- 더 복잡한 질의는 어떻게 다룰까?
- 만약 multiple ancohor node에서 출발하면?
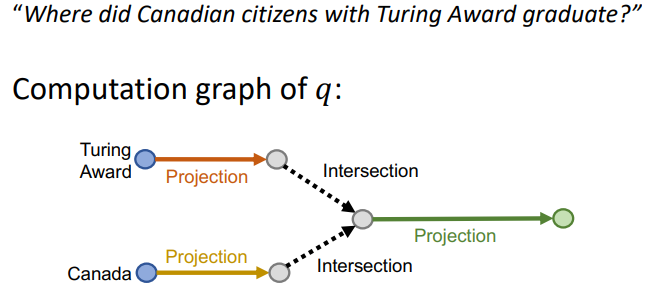
- 과정을 살펴보자
- anchor node 각각 출발하여 두 relation이 겹치는 node를 찾는다
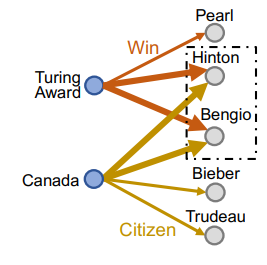
- multi-hop을 진행한다
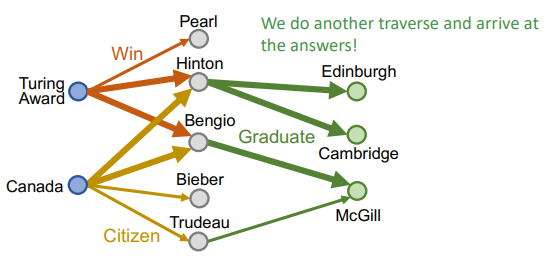
- anchor node 각각 출발하여 두 relation이 겹치는 node를 찾는다
Traversing KG in vector space
-
Computation grpah와 embedding space를 동시에 비교해보자
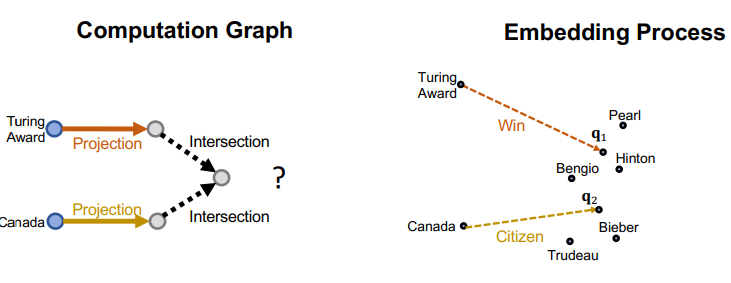
-
Q) 실제 임베딩 space에서 점 하나로 딱 떨어지지 않는데 뭐가 정확한 intersection인가?
- A) 아몰랑 Neural Net이 해결해주실거야
Neural intersection operator
- 여러 query를 받아서 intersection을 찾아야 한다
- 전지전능 neural intersection operator 를 모델링하자
- Input: query embedding set
- Output: intersection embedding
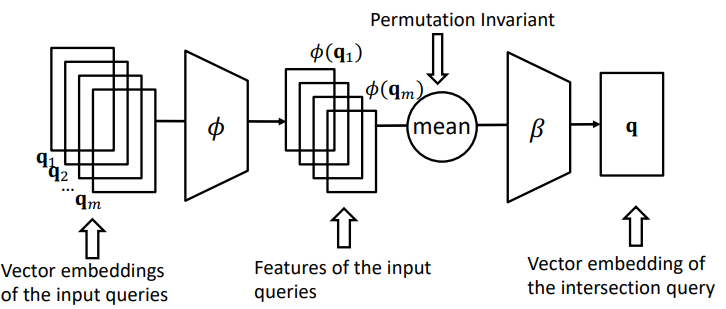
- 그러면 우린 성공적으로 intersection을 찾을 수 있다
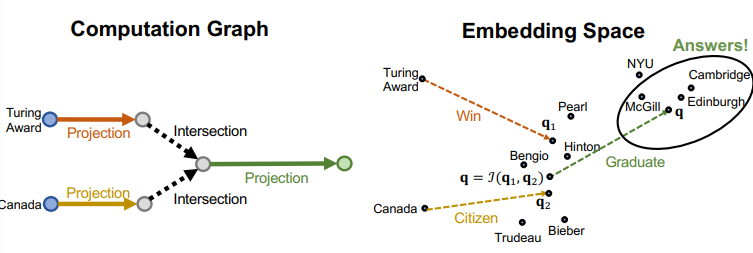
Training
- entity embedding 와 query embedding 가 주어졌을 때
- score function =
- parameters
- entity embedding:
- relation embedding:
- intersection operator φ, β: 그래프 사이즈에 영향받지 않음
- TransE하고 똑같이 학습하면 됨
- query q, answer v, negative sample v'를 샘플링한다
- q를 임베딩한다
- v와 v' score를 구한다
- loss 최적화 한다
- Evaluation
- test query q를 임베딩한다
- 모든 triple v에 대하여 score를 구한다
- ditance rank를 구하여 prediction한다
- Limitations
- 단순히 intersection vector 하나 구하는 것은 직관적이지 않음
- 정답이 될 수 있는 후보군을 추릴 수 없을까?
- 기하학적으로 더 설득력있는 답을 내놓고싶은데...
Query2Box
Box Embeddings
- query를 box로 임베딩하자
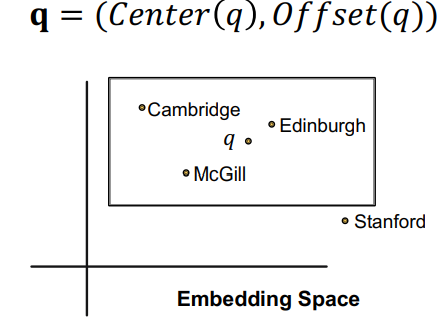
- 기존 intersection vector를 구하는 방식에 비해 더 직관적이다!
Embed with Box
- parameters
- entity embedding: 크기가 0인 box로 초기화
- relation embedding: center와 offset때문에 2개씩 만든다
- intersection operator φ, β: 그래프 사이즈에 영향받지 않음
- input으로 box를 받아서 output으로 box를 뱉을 예정
Projection operator
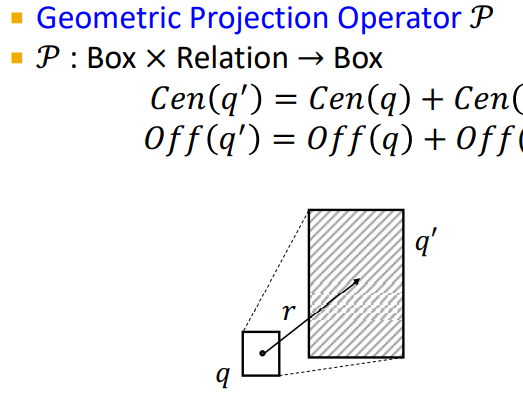
- path가 진행될 수록 box는 계속 커지며 간단히 생각해서 error에 해당되는 부분이라고 보면 된다
Embed with Box
- 기존 intersection vector를 구하는 방식과 달리 box를 임베딩하였다
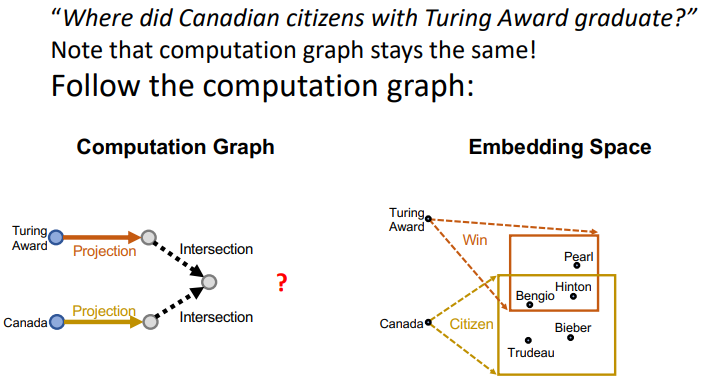
- 모든 box의 교집합 부분을 intersection box로 본다
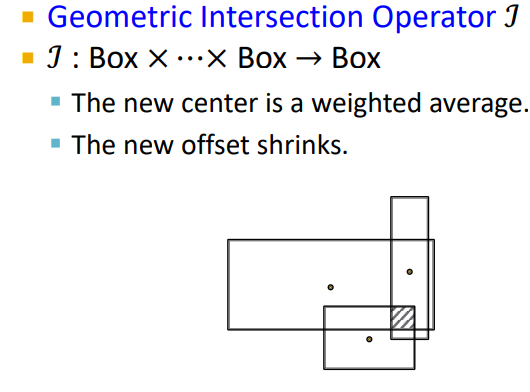
- center는 weighted average로 정한다
- new offset은 줄어든 것을 알 수 있다

- 이를 embedding space 관점에서 살펴보자
- intersection box를 구하고, 다음 매핑에서 새로운 box를 만들었다
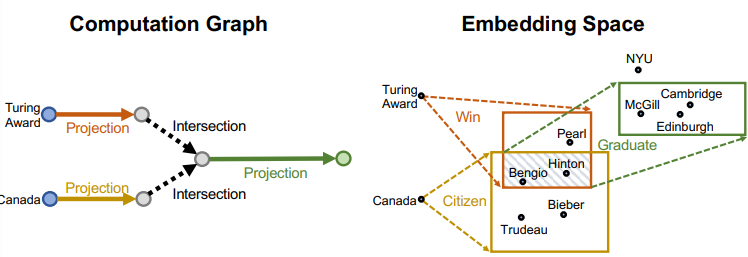
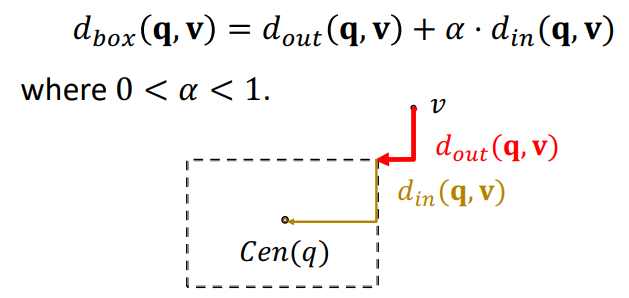
Entity-to-Box distance
- query box 와 entity vecotr 가 주어졌을 때 distance를 구해보자
- 에서 시작해서 까지의 L1 norm을 distance로 정의할 수 있고 알파를 조절하여 box 의 영향을 조절할 수 있다
Training
- loss를 minimize하는 방식으로 학습한다
- 좌항에서 true box score를 minimize하고, 우항에서 false box score를 maximize한다
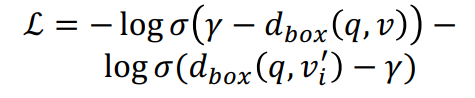
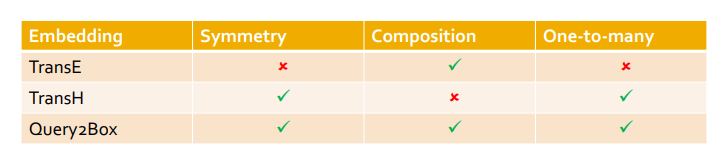
Relation patterns
- 결론 Leskovec 교수가 갓이다
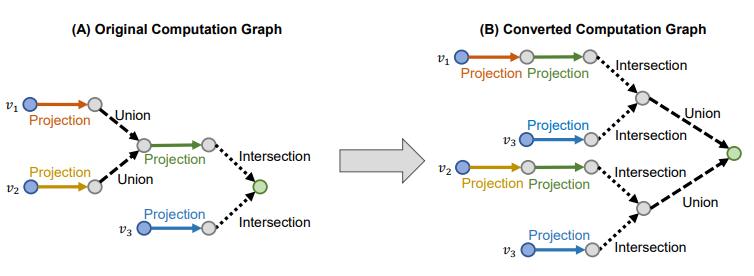
EPFO queries
- Existential Positive First-order (EPFO) : Conjunctive queries + disjunction
- 기존 embedding 방법으로 처리할 수 있다
- Process
- 모든 union이 걸린 노드마다 최종 목적지인 를 선택한다
- 모든 union edge를 제거한다
- 모든 union node를 순회하면서 와 로 새로운 compuation graph를 조직한다
- 쉽게 생각해서 모든 경우의 수를 따로 나누어서 graph를 만든다고 보면 된다

Knowledge Graph는 지식을 그래프 형태로 구성한 것으로,node가 entity 가 되며,edge가 relationship 이 됩니다.𝒉(head entity), 𝒍(relation), 𝒕(tail entity) =
(𝒉, 𝒍, 𝒕)node 와 relationship 을 triplet 형태로 표현합니다.
Knowledge Graph 에서는 Link Prediction 이 활발하다고 합니다.
TransE
(𝒉, 𝒍, 𝒕) 를 임의의 차원으로 mapping 하는 embedding 방법론으로,
Valid triplet 이 클수록, Corrupted triplet 이 작을수록 좋아지도록 margin loss 를 설정합니다.
transE 는 Composition Relations, 즉 relationship 간의 관계를 형성함으로써 또 다른 relationship 을 표현할 수 있다는 장점이 있지만,
Symmetric Relations 과 N-array Relations 를 표현할 수 없습니다.
TransR
TransR 은 entity 와 relation 을 동일한 semantic space 에 두지 않고, 구분된 공간에 embedding 하는 방법입니다.
Symmetric Relations 및 N-array Relations 을 표현할 수 있다는 장점이 있지만, Composition Relations 를 표현할 수 없습니다.
Path Queries
multi-hop reasoning 을 진행하기 위한 방법론이며, one-hop 을 일반화하여 여러 단계로 나누어 path 를 구성하여 질의를 진행합니다.
one-hop 을 여러 번 타고 타고 계산하는 방식은 시간복잡도 측면에서 비효율적이기 때문에,
query embedding하여 계산하는 방식으로 진행합니다.Conjunctive Queries
더욱 복잡한 질의의 경우 (교집합), 1. intersection 을 찾고 2. multi-hop 을 진행합니다.
이 때, 실제 embedding space 에서 하나의 점으로 표현되지 않기 때문에,
Neural Intersection Operator를 이용해 이를 해결합니다.각각의 query 마다 embedding 을 진행하여 neural network 를 통과시키고, 이를 통합하여 intersection query 를 만들어 냅니다.
Query2Box
intersection vector 하나만 구하는 것은 직관적이지 않기 때문에,
query를box로embedding하여,intersection box를 사용합니다.query box q 와 entity vector v 에 대하여, v 를 q 로 나타내고자 할 때, Entity-to-Box distance를 고려합니다. parameter α 를 통해 q 의 offset (=영향력, 중요도) 를 조절할 수 있습니다.
Query2Box 또한, Positive Box 를 maximize 하고, Negative Box 를 minimize 하는 Loss 를 설정해 training 을 진행합니다.
그천 (그래프 천재) 윤종님 띵강 감사감사 합니다 ~