1. Word2Vec

tobigs-nlp-article·2022년 1월 24일
0
post-thumbnail

오늘 다뤄볼 논문은 이제는 거의 고전 수준이 되어버린(사실 그렇게 엄청 오래된 논문은 아니지만 이 바닥에선 고전이라고 할 수 있을 것 같다.) word2vec이다. 방법론 자체가 지금의 기준으로 엄청 참신하다거나 너무 새로워서 모든 related work를 살펴봐야 할 수준은 아니다. DNN만 제대로 이해하고 있다면 충분히 논문을 이해할 수 있을 것이다. 다만, 단어를 벡터화시키는 그 발상이 BERT나 GPT로 대표되는 최근의 트렌드에서도 여전히 매우 유효한 개념인 것 같아서 중요하게 다뤄볼만한 논문이라고 생각한다. 그러므로 모델 구조와 수식을 엄청 자세히 뜯기보다 모델과 데이터의 설계를 중심으로 살펴보도록 하자.

기존의 word2vec은 Mikolov의 논문(Efficient Estimation of Word Representations in Vector Space)에서 제시되고, 이후에 Mikolov가 이 논문(Distributed Representations of Words and Phrases and their Compositionality)에서 개선한 것으로 알려져있다. 이 글에서도 대략적인 모델의 구조는 초기 논문을 따르고, 이후 개선 사항에 대해서만 뒤의 논문을 참고했다.

0. Atomic units of NLP

우선 자연어 처리가 기존의 이미지나 숫자 데이터와 어떤 점에서 다른지 살펴보도록 하자. 자연어 처리는 인간의 언어인 자연어를 컴퓨터가 처리하는 방법을 연구하는 분야이다.

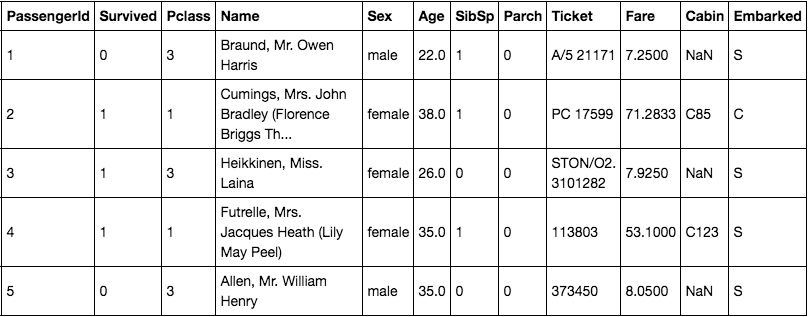
당연한 이야기지만, 숫자 데이터는 Titanic 데이터의 pclass, fare와 같이 숫자로 되어 있다. fare는 금액에 해당하는 데이터이기 때문에 연속형, pclass는 등급에 해당하는 데이터이기 때문에 이산형 데이터다. 두 데이터 종류가 조금은 차이가 있지만 컴퓨터가 처리하는데 있어서 데이터 그대로 처리가 가능하다는 점에서는 큰 차이가 없다. 즉, 3등급 좌석보다 1등급 좌석이 좋고, 7달러보다 1달러가 작은 금액이므로 그대로 모델이 처리할 수 있다.

하지만 자연어의 경우엔 그렇지 못하다. 자연어는 더하기, 빼기, 곱하기, 나누기와 같은 기본적인 연산이 불가능하기 때문에 일정한 처리를 통해 모델링에 사용하게 된다. 이때 가장 작은 요소인 자연어를 분리하여 사용한다. 즉, 코퍼스 -> 문단 -> 문장 -> 단어 -> 토큰 단위로 점점 데이터를 쪼개고, 가장 작은 토큰 단위로 데이터를 처리하게 된다.

1. Distributed Representation of Words

토큰 단위로 데이터를 처리할 때 가장 단순한 방법은 One Hot Encoding이다. 즉, 학습 데이터에 존재하는 각 토큰을 모두 모아서 vocab을 구성하고, 이 vocab에서 각각의 토큰마다 개별적은 인덱스를 부여하여 사용할 수 있다. 만약 전체 vocab의 크기가 5라면 [1 0 0 0 0][0 1 0 0 0]과 같이 토큰을 one hot vector로 변환해 컴퓨터가 인식하도록 만들 수 있다. 실제로 대부분의 트리 기반 모델은 이러한 전처리를 거쳐 자연어(정확하게는 범주형 변수)를 다룬다.

하지만 one hot vector는 다음과 같은 여러가지 문제점을 가지고 있다.

  • 저장해야 할 데이터가 너무 크다.
    우리는 5개의 토큰을 예시로 들었기 때문에 이게 무슨소리인가 할 수 있다. 하지만 현재 표준적인 vocab의 크기는 3만개 내외이다. 즉, 한 단어를 표현하기 위해서 해당 토큰의 인덱스만 1인 크기가 3만인 벡터를 사용해야 한다. 한 문장이 10개의 토큰으로 구성되어 있다면 30000×1030000\times 10의 행렬로 표현하게 된다.

    지난 투빅스 프로젝트 때 330만개 코퍼스로 학습을 진행했는데, 각 코퍼스 당 대략 30문장으로 구성되어 있다고 하면, 3300000×30×300003300000 \times 30 \times 30000 크기의 텐서가 필요해지는 것이다. 상당히 큰 텐서가 되고, 모델링하는데 무척 오래 걸릴 것이다.

  • 정보가 거의 없다.
    모델링하는데 오래 걸리는 것은 사실 큰 문제가 아니다. 그냥 좋은 gpu를 사용하면 된다. 하지만 이때 이용할 수 있는 단어의 정보가 매우 적다면 문제가 된다. 모델링이란 input의 정보를 가공하여 output에 매칭시키는 작업인데, 사용할 수 있는 정보가 적으니 제대로 매칭될 리가 없다.
    one hot vector가 표현하는 유일한 정보는 a 단어와 b 단어가 다른 단어이다 라는 정보가 유일하다. 하지만 실제로 인간은 언어를 사용함에 있어 정말 다양한 정보를 다루게 된다. 각 단어가 가진 의미도 있을 것이고, 문장에 맞는 문법을 구사하기 위해 동일한 단어를 변형시키기도 한다. 하지만 이러한 정보는 one hot vector에는 전혀 담기지 않는다.

위 두가지 문제로 인해 단어를 다른 방식으로 벡터화하려는 노력들이 있었다. 가장 대표적으로는 각 문서별 단어의 표현 빈도를 나타내거나, tf-idf를 이용해 보다 정교화해서 사용할 수도 있다. 하지만 이러한 방법들은 오늘 소개할 word2vec에 비하면 여전히 정보를 온전히 담고 있지 못하다.

word2vec은 무엇보다 분산표상(distributed representation)이라는 개념을 이용해 단어를 벡터화한다. 분산표상이란 한 단어의 의미는 함께 사용되는 단어를 통해 유추할 수 있다는 것이다. 즉, 단어의 의미는 그 단어 자체에 있지 않고 그 단어와 함께 사용되는 다른 단어들에 있다. 이에 대해선 언어학이나 비교문학 등에서 자세히 다룬다고 하는데, 이 정도만 하고 넘어가자.

2. Word2Vec

어쨋든 word2vec이 분산표상을 이용하는 방식은 거칠게 표현하면 다음과 같다.

  1. 모든 토큰에 일정 크기의 랜덤한 값을 가지는 벡터를 할당한다.
    d = 512라 하면 학습 데이터의 모든 토큰에 512 차원의 임의의 벡터를 할당한다.
  2. 일련의 학습과정을 거친다.
  3. 학습을 마친 벡터는 각 토큰들이 사용되는 문법적, 의미적 정보를 가지게 된다.

간단하다. 그냥 두 단계를 통해 완성된다. 이때 word2vec은 크게 skip-gram과 cbow로 방식이 나눠지는데 이는 2번에서 학습 방식을 달리하여 나눠진다.

2번의 자세한 내용을 정리하면 다음과 같다.

  • 동시에 등장하는 단어의 정의
  • 학습 과정의 정의
    이 두가지를 중점적으로 다루면서 하나씩 살펴보도록 하자.

word2vec은 크게 두가지 모델로 구분되지만, 두 모델이 학습하는 원리엔 공통적으로 위에서 언급한 단어의 의미는 함께 사용되는 단어에 있다는 철학을 공유합니다. 이를 다음 문장을 통해 좀 더 자세히 알아봅시다.

I want ___ food tonight

위 문장에서 빈칸에 들어갈 알맞은 단어는 다음 중 무엇일까요?

  1. itailian
  2. mexican
  3. chair
  4. coffee

당연히 1번이나 2번일 것입니다. 그 이유는 빈칸의 주변을 살펴보면 "밤에 먹음직스러운 음식"에 해당하는 단어가 빈칸에 적합하기 때문입니다. 즉, 빈칸에 들어갈 italian이나 mexican은 "밤에 먹음직스러운 음식"이라는 정보를 가지고 있는 단어일 것입니다. 한 단어의 의미는 독립적으로 존재하지 않고, 함께 사용되는 단어를 통해 파악할 수 있습니다!

2-1. 중심단어/주변단어

word2vec은 동시에 등장하는 단어를 중심단어와 주변단어라는 용어로 표현합니다. 아래와 같은 문장이 있다고 합시다.

Colorless green ideas sleep furiously

총 6개의 토큰(Colorless, green, ideas, sleep, furiously)으로 이루어진 문장입니다. 이때 기준이 되는 단어를 중심단어, 중심단어와 동시에 등장하는 단어를 주변단어라고 정의합니다.

즉, 한 문장에 같이 등장하는 단어라고 해도 항상 동시에 등장하는 단어라고 여기지 않습니다. 그럼 어디까지가 동시에 등장하는 단어일까요? 윈도우 사이즈를 통해 이를 정의합니다. 윈도우 사이즈란 하이퍼 파라미터로 중심단어로부터 윈도우 사이즈만큼 떨어진 토큰만 동시에 등장하는 단어라 간주하고 주변단어로 여깁니다. 예를 들어 윈도우 사이즈가 1이고, 중심단어가 green이라면 아래와 같이 green 양 옆으로 1 토큰 이내에 위치한 colorless, ideas만 green의 주변단어가 됩니다. 이를 정리해보면 다음과 같습니다.

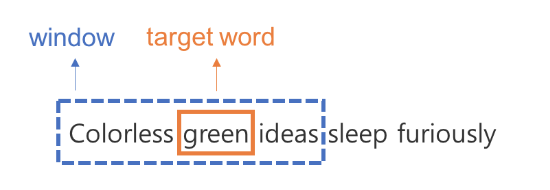
이러한 과정을 각 토큰을 중심 단어로 보고 주변단어를 매번 정리할 수 있습니다. 그 결과는 다음과 같습니다.

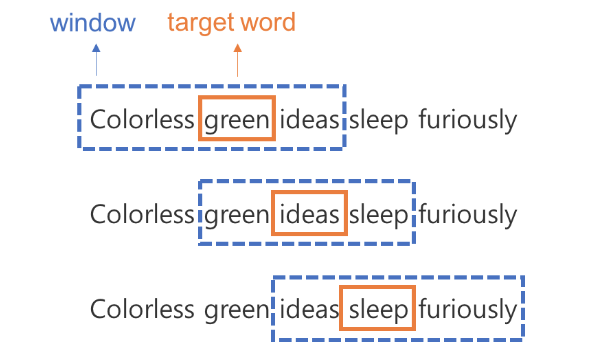
즉, 하나의 문장에서 학습 데이터가 위와 같이 여러 개 나오게 됩니다. 중심단어 하나에 윈도우 사이즈 X 2 만큼의 주변단어가 존재한다는 점을 기억해주세요.

2-2. CBOW

위에서 동시에 등장한 토큰을 정의했는데, 어떤 방식으로 학습하면 벡터에 토큰들의 문법적, 의미적 정보를 담을 수 있을까요? CBOW는 주변단어들의 정보로 중심단어를 맞추는 과정을 통해 이러한 정보를 벡터에 녹일 수 있다고 간주합니다.

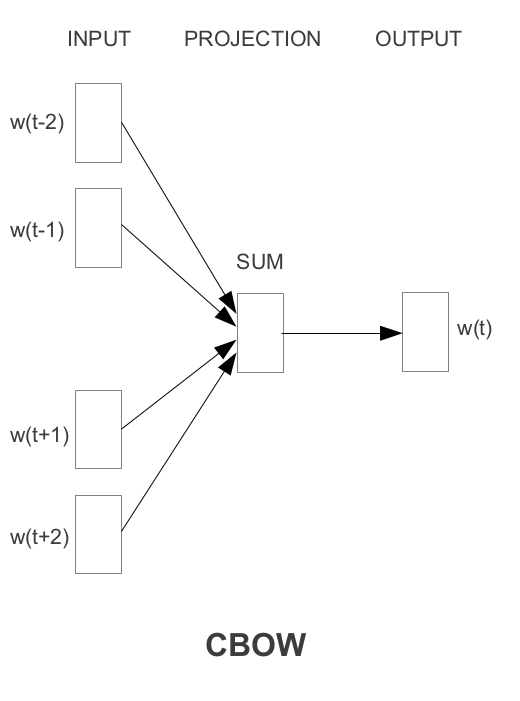
2-2-1. 모델 구조

  • input(1×V1 \times V) : input은 토큰의 인덱스에 해당하는 원소만 1인 one hot vector입니다.
  • input과 hidden layer 사이의 가중치 WV×MW_{V \times M} : 이 가중치는 모든 토큰의 임베딩 벡터를 행으로 가지는 행렬입니다.
  • hidden layer와 output 사이의 가중치 WM×V′W'_{M \times V} : 이 가중치는 반대로 모든 토큰의 임베딩 벡터를 열로 가지는 행렬입니다.
  • output($ 1 \times V$) : output은 입력 토큰의 벡터와 각 토큰의 유사도를 계산한 값입니다.
  • 최종 출력 : 위 그림엔 나와있지 않지만 output은 softmax 함수를 통과하여 최종적인 출력을 가지게 됩니다.

모델 구조를 입력부터 살펴보면 다음과 같은 흐름을 가집니다.

  1. 우선 주변 단어 각각이 one hot vector로 입력됩니다.
  2. 입력된 one hot vector 들은 WV×MW_{V \times M}와 행렬곱을 수행합니다. 이 과정을 통해 각 단어의 인덱스에 해당하는 WV×MW_{V \times M}의 행만 나오게 됩니다((1×V)(V×M)(1 \times V)(V \times M) = (1×M)(1 \times M)). 즉 각 단어의 임베딩 벡터를 가져옵니다.
  3. 각 주변단어의 임베딩 벡터를 합 혹은 평균합니다. 이를 통해 주변 단어의 정보를 하나의 벡터로 표현합니다.
  4. 이렇게 주변단어의 정보를 가지고 있는 벡터((1×M)(1 \times M))를 다시 WM×V′W'_{M \times V}와 곱하여 다음 레이어로 통과시킵니다((1×M)(M×V)=(1×V)(1 \times M)(M \times V) = (1 \times V). 이 과정에서 두번째 가중치 행렬 W'는 각 열에 모든 임베딩 벡터를 가지고 있다는 점을 생각합시다. 즉, 4번 과정은 주변단어의 정보를 각 임베딩 벡터와 내적하는 과정이라 할 수 있습니다.
  5. 그 결과 만들어진 output vector (1×V)(1 \times V)는 주변단어의 정보와 각 토큰의 normalize되지 않은 코사인 유사도를 나타냅니다(코사인 유사도에 대한 정보는 여기). 개념이 어렵다면 그냥 output vector는 주변단어의 정보가 모든 토큰들과 어느정도로 유사한지를 담고 있는 벡터라고 생각합시다.
  6. 이러한 벡터를 softmax 함수에 통과시키면 중심단어로 올 단어의 확률분포가 만들어집니다. 즉, 주변단어로 중심단어를 예측했습니다.
  7. 이를 실제 중심 단어 one hot vector를 이용해 cross entropy를 구하여 역전파 시킵니다.

2-2-2. 임베딩 벡터

모델 구조에서 이야기했듯이, cbow는 두가지 임베딩 벡터를 가지고 있습니다.
W와 W'인데, W는 주변단어일때의 임베딩 벡터이고, W'는 중심단어일 때의 임베딩 벡터로 간주합니다. 실제로 임베딩 벡터를 사용할 때는 W만 단독으로 사용하거나, W + W'를 사용하게 됩니다.

2-3. Skip-Gram

하지만 이런 식으로 학습이 진행되면 조금 아쉬운 점이 있습니다. CBOW는 입력값으로 다수의 단어 벡터를 사용하는 과정에서 아래와 같은 복잡도를 가지게 됩니다.

N×D+D×log2(V)N \times D + D \times log_2(V)

여기서 N = 윈도우 사이즈, D = 임베딩 벡터 크기, V = 보캡 크기 입니다. 그래서 Skip Gram은 이를 개선하여 연산속도를 빠르게 하면서 비슷한 학습 과정을 거치도록 설계했습니다.

D+D×log2(V)D + D \times log_2(V)

자세한 내용은 아래에서 설명하도록 하겠습니다.

2-3-1. 모델구조

Skip-Gram은 CBOW의 모델 구조를 뒤집었습니다. 즉, 중심단어를 입력으로 하여 주변단어를 예측하는 과정을 수행합니다. 우선 수식으로 살펴보자면 다음과 같습니다.

1T∑t=1T∑−c≤j≤c,j≠0log⁡p(wt+j∣wt){1\over T}\sum^T_{t = 1}\sum_{-c\leq j\leq c, j \neq 0}\log p(w_{t+j} \mid w_t)

식은 아래에서 다시 이야기하기 위해 꺼내온 거라 여기서 깊게 이해할 필요는 없습니다. 그냥 t 시점의 단어가 조건으로 걸려서 t+j 시점의 단어의 확률을 계산하는 식이라는 점만 명심합시다. 이를 보기 편하게 그림으로 나타내면 아래와 같습니다.

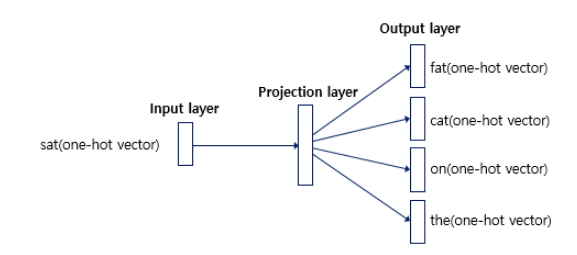
여기서 가중치 벡터나 모델의 순전파 방식은 거의 동일합니다. 다른 점만 이야기해보면 다음과 같습니다.

  1. input으로 중심단어를 사용하기 때문에 hidden layer의 벡터는 중심단어의 임베딩 벡터가 됩니다.
  2. CBOW와 다르게 input으로 하나의 단어만 사용되기 때문에 더하거나 평균을 구하는 과정이 없습니다.
  3. CBOW와 다르게 주변단어를 예측하기 때문에 softmax를 통과한 확률분포는 모든 주변단어와 손실값을 계산하여 역전파가 이루어지게 됩니다.

2-3-2. 장점

이를 통해 중심단어와 주변단어의 관계를 통해 학습이 이루어지는 CBOW의 학습 과정은 거의 모사하되, input으로 사용되는 one hot vector를 N개에서 1개로 줄여 연산량을 줄일 수 있었습니다. 또한, 모델 성능에서도 CBOW보다 Skip-Gram이 훨씬 잘 잡아내는 모습입니다.

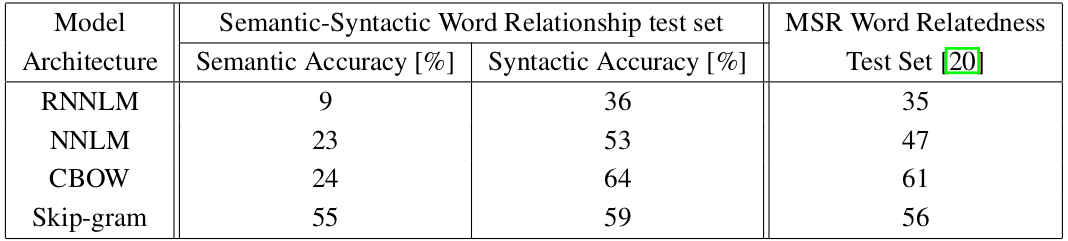
의미적 정보에서 Skip-Gram이 월등히 앞서면서 문법적 정보에선 아주 조금 밀리는 모습을 보입니다.

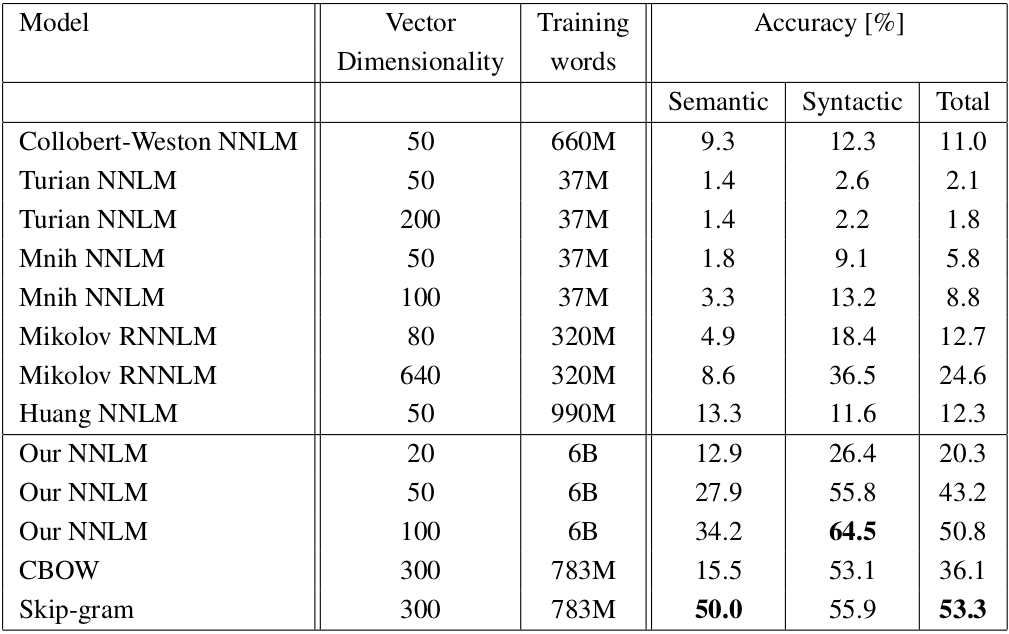
여기선 Skip-Gram이 CBOW보다 훨씬 성능이 좋은 모습입니다.

3. 모델 개선

3-1. Details of Skip-Gram

결국 현재 이야기하는 word2vec은 대부분 skip-gram을 이야기하게 됩니다. CBOW보다 성능이 동등하거나 좋으면서, 연산량은 훨씬 적어지니까요. 그래서 우린 skip-gram을 좀 더 뜯어보도록 하겠습니다. 위에서 언급한 식부터 시작합시다.

1T∑t=1T∑−c≤j≤c,j≠0log⁡p(wt+j∣wt){1\over T}\sum^T_{t = 1}\sum_{-c\leq j\leq c, j \neq 0}\log p(w_{t+j} \mid w_t)

Skip-Gram의 목적식은 위와 같습니다. 일반적인 딥러닝의 목적식이 최소화를 목표로 하는 것과 반대로 위 식은 최대화를 목표로 진행하게 됩니다. 즉, t시점의 중심단어 wtw_t가 등장했을 때, 주변단어 wt−cw_{t-c} ~ wt+cw_{t+c}가 등장할 확률(이때 c는 윈도우 사이즈입니다.)을 최대화하도록 파라미터가 최적화되게 됩니다. 여기서 이 식을 좀 더 뜯어보면 Skip-Gram이 softmax 함수를 이용하기 때문에 해당 부분은 아래와 같이 쓸 수 있습니다.

p(wO∣wI)=exp(vwO′TvwI)∑w=1Wexp(vx′TvxI)p(w_O \mid w_I) = {{exp(v_{wO}^{'T}v_{wI})} \over {\sum^W_{w = 1} exp(v^{'T}_xv_{xI})}}

위 식에서 wIw_{I}는 skip gram에서 중심단어, wOw_O는 주변단어입니다. 또한, vv가 입력 시 임베딩 행렬이고 v′v'는 hidden layer와 output layer 사이의 임베딩 행렬입니다.

3-2. Hierarchical Softmax

위에서 설명한 소프트맥스 함수를 미분하려면 꽤 많은 연산량이 필요하다고 합니다(자세한 내용은 softmax 층의 미분및 그래디언트 역전파 관련 자료를 찾아보면 이해하기 편할겁니다. ratsgo님의 블로그에도 아주 자세하게 나와있습니다.).

Skip-gram에서 소프트맥스 함수는 O(V)O(V)의 복잡도를 가지게 됩니다. 중심단어의 임베딩 벡터와 보캡 내 모든 단어의 임베딩 벡터를 내적해야 하기 때문입니다. word2vec의 경우 BPE와 같은 방법론을 사용하지 않기 때문에 보캡의 크기가 100만 단위 이상이 되기 때문에, 이러한 복잡도는 부담이 될 수 밖에 없습니다.

그래서 일종의 트릭으로 softmax 함수를 변환시켜 연산량을 줄인 것이 hierarchical softmax입니다(귀찮으니까 앞으로 h-softmax로 표현하겠습니다.). h-softmax의 기본적인 아이디어는 다음과 같습니다.

  1. softmax는 확률분포를 리턴하도록한다.
    즉, 출력 벡터의 합이 1이고, 원소들이 0 ~1dlaus ehlqslek.
  2. 트리 구조를 활용하여 복잡도를 log2(V)log_2(V)로 낮추자.

즉, 이진분류 트리구조를 도입해서 확률분포를 계산하도록 softmax 함수를 변형한 것이 h-softmax입니다. 그림으로 먼저 이야기해봅시다.

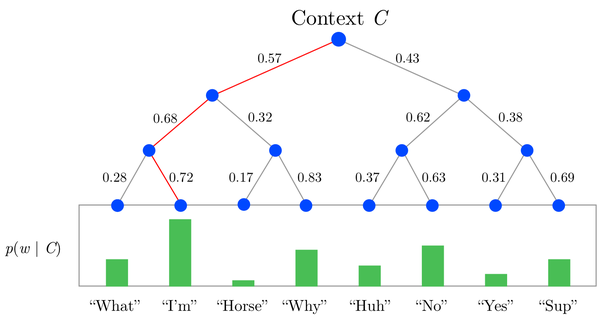
h-softmax에서 중심단어 C가 주어졌을 때, 주변 단어 I'm이 나올 확률(p(I′m∣C)p(I'm \mid C))는 위와 같이 표현할 수 있습니다. 각 엣지의 의미는 해당 부모노드에서 자식노드로 갈 확률을 의미합니다. 즉, 0.57의 엣지는 중심단어 C가 주어졌을 때 What ~ Why에 이르는 단어가 등장할 확률을 의미합니다. 0.68 역시 What ~ Why중에서 What ~ I'm이 등장할 확률을 의미합니다. 한번에 p(I′m∣C)p(I'm \mid C)를 계산하지 않고, 단어 집합 중에 등장할 확률로 변환하여 여러 단계로 구성한 것이 h-softmax입니다.

이 과정은 결국 이진트리에서 해당하는 리프노드를 탐색하는 과정과 동일한 복잡도를 가지기 때문에 O(log⁡2(V))O(\log_2 (V))가 됩니다.

이를 식으로 다시 한번 보면 아래와 같습니다.

p(w∣wI)=∏j=1L(w)−1σ([[n(w,j+1)=ch(n(w,j)]]⋅vn(w,j)′TvwI)p(w \mid w_I) = \prod^{L(w) - 1}_{j =1} \sigma([[n(w, j+1) = ch(n(w, j)]] \cdot v^{'T}_{n(w, j)}v_{wI})
  1. 여기서 모든 단어는 리프 노드에 위치합니다.
  2. L(w)L(w):루트노드에서 단어노드까지 경로 길이를 의미합니다.
  3. n(w, i) : w 단어노드로 가는 경로 중 i번째 노드를 의미합니다. 즉, n(w, 1)은 루트노드이고, n(w, L(w)) = w가 됩니다.
  4. [[x]] :True, False 반환함수 입니다. 함수 입력값이 True면 1, False면 -1을 반환합니다.
  5. ch(n) :노드 n의 자식노드들을 의미합니다.
  6. 각 노드는 모두 임베딩 벡터와 동일한 크기의 벡터를 가지고 있습니다.

위 식과 항들을 조합해면 h-softmax는 루트노드에서 시작하여 모든 노드를 따라 내려오면서 각 노드의 임베딩 벡터와 중심 단어의 임베딩 벡터를 내적한 값을 통해 확률을 표현하고 있습니다.

이전의 소프트맥스 함수가 모든 단어에 대해 중심 단어와 내적값을 구해 확률분포를 표현했던 것에 비해, h-softmax는 주변단어의 경로를 이미 알고 있기 때문에 그 경로를 따라서만 확률을 계산하면 p(I′m∣C)p(I'm \mid C)를 구할 수 있습니다.

결과적으로 이렇게 구성하게 되면 우리는 정답 레이블에 해당하는 주변 단어의 확률을 구하는 과정에서 주변 단어가 아닌 단어에 대한 연산을 할 필요가 없어집니다. 왜냐하면 위 그림에서 표현되어있듯이 모든 단어의 확률의 합은 1로 보장이 되기 때문입니다. 어차피 우리가 이진트리를 통해 구한 값이 확률임이 보장되기 때문에, 굳이 기존의 소프트맥스 함수처럼 모든 단어의 확률을 구하지 않습니다.

실제로 소프트맥스의 역전파 과정은 레이블에 해당하는 확률을 통해서만 역전파가 이뤄지기 때문에 이와 같은 연산의 변화가 효과적이기도 합니다.

3-3. Negative Sampling

3-3-1. Binary Classification

네거티브 샘플링은 h-softmax보다 연산량을 더 줄이고자 도입된 방법론입니다. 기존 skip gram의 목적함수를 다시한번 가져와보겠습니다.

1T∑t=1T∑−c≤j≤c,j≠0log⁡p(wt+j∣wt){1\over T}\sum^T_{t = 1}\sum_{-c\leq j\leq c, j \neq 0}\log p(w_{t+j} \mid w_t)

기존 skip gram의 목적함수를 보면, 결국 중심단어와 주변단어의 log 확률을 최대화하는 구조임을 알 수 있습니다. 이 구조는 중심-주변단어의 쌍만 사용해서 모델링합니다. 즉, 호주-캥거루의 관계를 학습하는 것이죠. 이를 위해서 중심단어를 입력값으로 하여 100만개의 단어 중 어떤 단어가 주변단어일지 예측하는 태스크를 수행합니다. 그리고 그 과정에서 중심단어와 주변단어의 임베딩 벡터 간 내적값을 크게 만드려고 합니다.

그런데, 어차피 중심-주변 단어의 벡터 간 내적값이 크면 된다면, 그냥 두 벡터를 내적해서 그 값을 키워도 되지 않을까요? 즉, 아래와 같이 목적함수를 구성해도 되지 않을까요?

1T∑t=1T∑−c≤j≤c,j≠0log⁡σ(vj′Tvi){1\over T}\sum^T_{t = 1}\sum_{-c\leq j\leq c, j \neq 0}\log \sigma(v^{'T}_{j}v_i)

복잡하게 조건부 확률을 구하지 말고, 그냥 벡터 내적해버리자는 이야기입니다(로그는 무시합시다.). 그리고 이를 확률로 표현하기 위해 시그마를 씌웁니다.

이를 통해 우리는 연산량 감소 효과를 가지게 됩니다. 소프트맥스는 거듭 말하지만 중심 단어 벡터와 100만에 달하는 모든 단어 벡터를 내적해야 합니다. 하지만 이처럼 시그모이드 함수를 이용하게 되면 중심-주변 단어 간의 동시 사용 여부를 판단하는 이진분류 태스크로 변하게 되고, 연산량도 획기적으로(h-softmax보다도 적습니다) 줄어들게 됩니다.

3-3-2. Not 주변단어

이렇게 연산량이 줄어드니, 좀 더 성능확보에 집중할 수 있게 되고, 그래서 네거티브 샘플링이 가능해집니다. 네거티브 샘플링의 아이디어는 다음과 같습니다.

중심-주변 단어의 내적값은 크게, 중심-not주변 단어의 내적값은 작게 만들자.

즉, 기존의 시그모이드를 씌우듯, 중심-not주변 단어의 관계도 함께 모델링하자는 겁니다. 소프트 맥스 함수를 사용하면 중심-not주변 단어의 관계도 학습한다는 점을 생각하면 이는 확실히 문제입니다.이를 통해 함께 사용되지 않는 단어들끼리 서로 연관성이 없다는 사실 역시 모델링이 가능해질 것입니다.

이를 위해 위의 식을 조금 변형하겠습니다.

log⁡σ(vwO′TvwI)+∑i=1kEwi∼Pn(w)[log⁡σ(−vwi′TvwI]\log \sigma(v^{'T}_{wO}v_{wI})+\sum^k_{i = 1}\mathop{\mathbb{E}}_{w_i \sim P_n(w)}[\log\sigma(-v^{'T}_{wi}v_{wI}]

식이 복잡해보이지만 어차피 앞의 항은 우리가 이미 본 항이니까 신경쓰지 않아도 됩니다. 뒤의 항은 중심단어와 주변단어가 아닌 단어 간의 내적 값을 계산하고, 그 값이 클수록 작아지는 항입니다. 우리는 목적식을 최대화 -> 각 항을 최대화 -> 뒤의 항을 최대화 -> 중심-not주변 단어 내적 값 최소화하면 되는겁니다.

이때 모든 not주변단어에 대해 계산할 수 없으므로(주변 단어가 아닌 단어는 너무 많으니까) 일정한 샘플링을 통해 k개의 not주변단어를 뽑게 됩니다.

3-3-3. Sampling

논문에선 두가지 방법으로 샘플링했다고 이야기하고 전체 데이터에서 각 단어의 출현확률3/4\text{출현확률}^{3/4}를 했을 때 가장 성능이 좋았다고 이야기하고 있습니다. 식으로 표현하면 아래와 같습니다.

Pn(w)=U(w)3/4P_n(w) = U(w)^{3/4}

(U(w)는 unigram dist.로 단어 별 분포입니다.

이렇게 샘플링하게 되면 한가지 문제가 발생합니다. 자주 출현하는 the, a, an, in과 같은 단어들이 자주 샘플링된다는 점입니다. 실제로 이러한 단어들이 가지는 정보는 거의 없기 때문에, 이러한 단어들과 함께 임베딩 벡터를 업데이트 해봐야, 효과적이지 않습니다. 함께 자주 출현하지 않더라도, in-Paris보단 paris-croissant을 업데이트하는 것이 파리라는 단어의 정보를 표현하는데 효과적일 것입니다. 즉, 어차피 자주 등장하는 단어는 매번 업데이트하지 않아도, 충분이 학습이 되고, 자주 출현하지 않는 단어를 업데이트하는데 아주 조금 더 집중하고자 했습니다.

이를 위해 단어의 출현 빈도에 따라 학습에서 제외될 확률을 다음과 같이 정의했습니다.

P(wi)=1−tf(wi)P(w_i) = 1 - \sqrt{t \over f(w_i)}

여기서 f는 해당 단어의 출현 횟수이고, t는 최소 출현확률입니다. 즉, t = 0.000001이라면, 0.000001 이상의 확률로 등장하는 단어만 학습에서 일부 제외하면서 학습합니다. 예를 들어 t = 0.000001이고, a, an, the처럼 자주 등장하는 단어의 등장확률(f(w) = 0.01)이라면 학습에서 제외될 확률이 무려 0.96이나 됩니다.

4. 시각화

https://nbviewer.org/github/dreamgonfly/phone-review-nlp/blob/master/phone_reviews_nlp.ipynb#Visualizing-word-vectors-with-t-SNE

https://ronxin.github.io/wevi/

**사실 네거티브 샘플링과 관련해서는 좀 더 엄밀한 수학적 가정 및 수식 전개를 통해 해당 식을 유도할 수 있습니다. 하지만 word2vec 모델에서 우리가 꼭 배워야 할 부분이라고 생각하진 않아서, 제외했습니다. 관심이 있으신 분들은 이 자료를 한번 살펴보시기를 추천드립니다.

참고자료

https://arxiv.org/abs/1301.3781 word2vec 1
https://arxiv.org/abs/1310.4546 word2vec 2
https://arxiv.org/abs/1411.2738 : 역전파 과정 자세히 설명(사실 열심히 안봄)
https://arxiv.org/abs/1402.3722
https://wikidocs.net/22660
https://dreamgonfly.github.io/blog/word2vec-explained/
https://ratsgo.github.io/deep%20learning/2017/10/02/softmax/

profile
tobigs-nlp-article
투빅스 NLP 논문세미나입니다!
다음 포스트

1. Word2Vec

0개의 댓글