작성자 : 권오현

Abstract

• Contextual Information을 활용하여 Online Personalized recommendation Servies (e.g., 온라인 광고, 뉴스 추천)를 제공하는 방법에 대하여 Contextual Multi-armed banit에 대한 관심이 증가하고 있다.

• 기존의 Contextual Multi-armed bandit은 특정한 context에 대해 arm의 reward를 예측하기 위해 보상 함수의 존재를 가정하는 경우가 많다.

• 하지만 Real-world 에서는 시간이 지남에 User의 선호도가 동적으로 변하는 경우가 많기 때문에 위와 같은 가정은 실제로 적용되는 경우가 거의 없다.

• 논문 저자는 시간에 따라 변화하는 보상 함수에 대하여 Time Varying Contextual Multi armed problem을 연구하였고 특히, Particle learning을 기반으로 한 dynamical context drift model을 제안하였다.

• 제안된 모델은 random walk particles set으로 모델링 되며, fitted particle이 reward function을 학습하도록 한다.

• Particle learning을 통해 모델이 context의 변화를 포착하는데 효과적이며 context의 latent parameters를 학습할 수 있다.

• 온라인 광고와 뉴스 추천에 대하여 제안한 방법론의 효과와 모델이 Time varying reward에 대해서 dynamically tracking 하여 결과적으로 CTR을 향상시킬 수 있다는 것을 보여준다.

[참고]

Multi-armed Bandit problem

Bandits

• MAB는 User가 어느 슬롯머신의 손잡이를 당겨야 가장 높은 수익을 올릴 수 있을지를 결정하는 알고리즘이다.
• MAB에서 가장 중요한 개념은 Exploration(탐색) & Exploitaion(활용)이다.

  • 만약 우리가 꽤 좋은 결과를 돌려주는 기계를 찾아냈다면 좋은 결과를 유지하기 위해 그 기계를 계속 사용할 것인지(exploitation) 아니면 더 좋은 결과를 얻을 거라는 희망으로 다른 기계를 찾아볼 것인가(exploration)?
  • Exploration은 다양한 정보를 수집하기 위해 불확실성이 높은 다양한 광고 콘텐츠를 보여주어 사용자들의 성향을 탐색한다. Exploitation은 사용자들이 많이 소비할 것 같은 광고, 인기 콘텐츠만 제공한다.

1. Introduction

• Online Personalized recommender systems은 User와 Item의 현재 정보에 따라 고객에게 적절한 feed(e.g., advertisements, news article)를 주어 고객의 만족을 극대화하려고 한다.

• 이러한 목표 달성을 위해 추천시스템에서 고객의 preferences에 대하여 instantly tracking 과 large item repository에서 흥미로운 아이템을 추천해주는 것이 중요하다.

• Consumer preference와 target items에 대해 적절히 매칭 시키는 것은 어렵다.

  1. Cold Start Problem
  2. 유행의 변화와 고객의 선호도가 dynamically changing

• context-based Exploration-Exploitation tradoff dilemma

  정보를 얻어 가장 좋은 승률을 가진 슬롯머신을 선택해야 하기 때문에 두 과정이 반드시 필요하며, 한 가지 과정을 완전히 배제해서는 원하는 결과를 얻을 수 없다.

• Contextual multi-armed bandit에 대한 여러 알고리즘이 연구됨 ($\epsilon-greedy$, LinUCB, Thompson Sampling)
  : 이러한 알고리즘들은 동일한 contextual information에서의 reward는 변하지 않는다고 가정한다. 즉, 시간에 따라 변화는 contextual information의 latent factor를 고려하지 않기 때문이다.
  

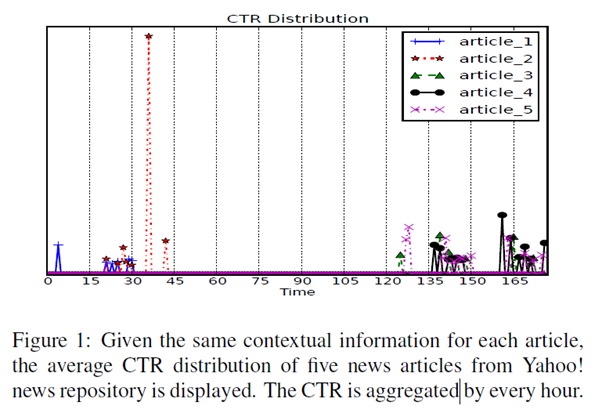
동일한 contextual information에 대하여 5개 뉴스의 CTR을 조사하였다.
Multi-armed bandit에서는 처음에 많이 선택된 article_1, article_2가 시간이 지나도 CTR이 높을 것이지만 시간이 지날 수록 article_1, article_2에 대한 CTR은 낮아지고 article_3, article_4, article_5에 대한 CTR이 높아지는 것을 확인할 수 있다.

• contextual multi-armed bandit problems의 Time varying reward를 포착 하기 위해 논문 저자들은 Particle Learning에 기반한 Dynamical context drift model을 제안하였고, 효과적인 Onlne 추론 모델을 개발하였다.

• Dynamical Reward에 대하여 random walk particles를 통해 모델링 하였고, Particle learning을 통해 context change와 latent parameters를 학습할 수 있다.

2. Related Work

• 논문에서 Reward의 dynamic한 상황을 해결하기 위한 Contextual Multi-armed bandit을 이용한 context drift model을 제안한다. Latent parameter를 학습하고 Latent States를 추론하기 위해 Sequential Online Method를 개발 하였다.

2.1 Contextual Multi-armed Bandit

• Multi-armed bandit은 다양한 분야에서 사용된다. (e.g., online advertising, web content optimizing, robotic routing)

• Multi-armed bandit의 가장 중요한 목적은 Exploration-Exploitation trade off 의 균형을 맞추는 것이다. 이러한 문제를 해결하기 위해 다양한 algorithms 제안됨 ($\epsilon$-greedy, UCB, EXP3, Thompson sampling)

• Contextual Multi-armed Bandit은 Contextual information을 통해 arm을 선택한다.

• Multi-armed bandit algorithms는 Context information을 통합하도록 확장되었다.

  • $\epsilon-greedy$ : $1-\epsilon$의 확률을 기반으로 Arm을 선택하고 $\epsilon$ 의 확률을 기반으로 random 하게 Arm을 선택한다. 즉, 현재 상황에 대하여 Best arm 선택(Exploitation), 충분한 탐색(exploration)을 위해 $\epsilon$을 선택한다

  • LinUCB, LogUCB : UCB algorithms, 탐색했던 arm으로 부터 얼마나 많은 reward 받았는지 뿐만 아니라 얼마나 확실한지도 함께 따져서, 덜 확실한 쪽에 더 많은 탐색을 하는 방법 , LinUCB는 arm의 reward와 context간에 coefficent vector를 이용하여 Linear Expected Reward를 계산하였다. LogUCB는 Logistic-regression으로 설명

  • Thompson Sampling : earliest heuristics, 각각의 arm에 대한 reward distribution의 parameters를 확률 변수로 보고 이 parameter distribution으로 부터 무작위로 추출하여 해당 값에 대한 reward의 기댓값이 가장 높은 arm을 선택하고, arm에 대한 parameter distribution을 업데이트함 $\rightarrow$ Bandit을 당길 경우를 $\theta_k$ 로 보면, $\theta_k$의 추정값에 대한 prior distribution을 $Beta$분포로 가정하면 conjugacy한 특성으로 인해 posterior distribution을 구할 수 있다.

  • 이외의 최신 연구들은 bootstrap sample와 같이 principled sampling approach하의 parameter-free algorithms을 다루고 있다.

• 하지만 이러한 알고리즘은 동일한 Contextual information하에서 Reward가 변하지 않는다고 가정하고 arm의 expected reward를 예측한다.

2.2 Sequential Online Inference

• Real-world 에서도 효과적인 모델을 위해 저자들은 Sequential Online inference를 사용하여 context의 latent state를 추론하고, model paramters를 학습한다.

  • Sequential Monte Carlo Method (SMC) :
    filtering problem을 해결하기 위해 제안된 Monte Carlo Method의 set. SMC는 posterior distribution을 계산하는 simulation method를 제공한다. 이러한 방법을 통해 general state space models에서 non-linear and non-Gaussian 일 수도 있는 posterior distribution을 구할 수 있다. (현실 세계의 정보를 반영하는 posterior 구할 수 있다.)

    Filtering problem : 해당 시스템에 대한 불완전하고 잡음이 많은 관측 세트에서 일부 시스템의 실제 값에 대한 "최상의 추정치"를 설정하는 것이다.
    Monte Carlo Method : Monte-Carlo method는 무작위 추출된 난수(Random Number)를 이용하여 함수의 값을 계산하는 통계학적 방법으로서, 수치적분이나 최적화 등에 널리 쓰인다.

  • Particle Learning :
    Particle Learning은 general state space models에 대한 sequential parameter learning 및 smoothing인 state filtering을 제안한다. Particle은 광범위한 state space models에 대한 parameter의 불확실성에 비추어 sequential filtering과 smoothing distribution을 통해 근사화 한다. Particle learning의 주요 idea는 resample-propagate framework에서 fixed parameters에 대한 조건부 통계와 particle의 근사를 통해 states에 대한 joint posterior distribution을 직접 샘플링하는 Particle algorithms을 만드는 것이다.

    

• 논문 저자는 Real-world에 대한 latent state inference와 parameter learning을 위해 particle learning 아이디어를 적용하였다.

3. Problem Formulation

• 저자는 Contextual Multi-armed Bandit Problem을 정의하고 Time varying contextual multi-armed badit problem을 정의하였다.

3.1 Basic Concepts and Terminologies

• $\mathcal{A}$ = {$a^{(1)}$,$a^{(2)}$, $a^{(3)}$,$\cdots$ ,$a^{(k)}$} , $k$ = The number of arms
  $x_{t} \in \mathcal{X}$, $x_t$는 t시점의 contextual information을 의미하고 $\mathcal{X}$는 d차원의 feature space
• Contextual Multi-armed bandit은 유한한 시간 범위 T에 대한 결정
• Policy function $\pi$는 $t \in [1, T]$의 t에 대한 arm을 결정($\pi(x_t)$)한다. arm을 pulling 한 후 policy function에 대한 reward를 받는다.
• t시점의 arm $a^{(k)}$의 reward는 $r_{k,t}$로 표현된다. $r_{k,t}$는 arm $a^{(k)}$에 제시된 context $x_{t}$에 의해 결정되는 미지의 분포로 부터 도출된다. 또한 $a^{(k)}$가 pulling 않으면 reward를 구할 수 없다.
• Total Reward $R_{\pi} = \sum_{t=1}^{T}r_{\pi(x_t)}$ , policy function $\pi$ 가 total reward인 $R_{\pi}$를 최대화 하는것이 목적이다.
• t시점의 arm을 선택하기 전에 policy function $\pi$는 일반적으로 과거 관측치인 $S_{\pi,t-1} = \left \{(x_i,\pi(x_i),r_{\pi(x_t)})|1\leq i < t \right \}$에 따라 모든 arm에 대한 보상을 예측하는 모델을 학습한다. Reward Prediction은 policy function $\pi$의 결정이 total reward를 증가시키는 것을 도와준다.
• $y_{k,t}$는 arm $a^{(k)}$의 predicted reward, $y_{k,t}$$=f_{a^{(k)}}(x_t)$ 로 표현된다. 즉, contextual information인 $x_{t}$가 reward function $f_{a^{(k)}}$의 input으로 들어간다.

  $f_{a^{(k)}}$의 방법중 하나는 feature vector의 linear combination이다.
  $ex)$ $f_{a^{(k)}}(x_t)$ = $X_t^{T}W_k + \varepsilon_k$ , $X_t^{T}$는 T 시점의 contextual information이고 $W_K$는 d-dimension의 coefficient vector, $\varepsilon_k \sim \mathcal{N}(0, \sigma^2_k)$, $y_{k,t} \sim \mathcal{N}(X_t^{T}W_k,\sigma^2_k)$

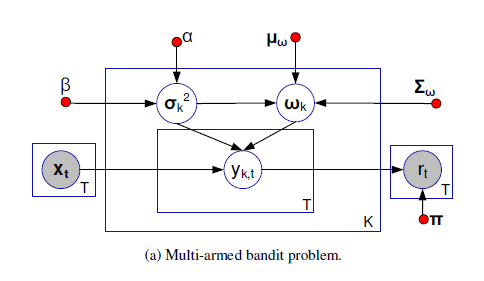
• 이러한 상황에서 Multi-armed bandit은 다음과 같이 표현된다. $X_t$는 t시점의 contextual information, predicted reward인 $y_{k,t}$ 는 random variable $X_t, w_k, \sigma^2_k$에 의해 결정된다.
• random variable인 $w_k, \sigma^2_k$ 의 conjugate prior distribution을 $\mathcal{NIG}$(i.e., Normal Inverse Gamma) distribution으로 가정한다. $\mathcal{NIG}(\mu_w,\sum_w,\alpha,\beta)$, 여기서 parameter들은 predefined함
• policy function $\pi$는 reward prediction model에 따라 arm $a^{(k)}$중 하나를 선택한다. t 시점의 arm $a^{(k)}$를 pulling하면, $r_{k,t}$가 구해진다. 이 후 새로운 sequence $(X_t, \pi(X_t), r_{\pi(X_t)})$ 가 구해져 $S_{\pi, t-1}(X_t, \pi(x_t), r_{k,t})$에 업데이터 되어 $w_k, \sigma^2_k$의 posterior distribution $\mathcal{NIG}$ distribution이 된다. 즉 , t시점의 $w_k, \sigma^2_k$의 posterior distribution이 t+1 시점의 prior distribtuion이 된다.

  Posterior Distribution의 parameter update 과정 :
  

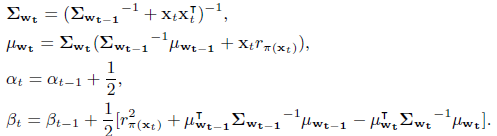
  • Thompson sampling : each arm $a^{(k)}$에 대하여 $w_k, \sigma^2_k$ 를 $\mathcal{NIG}$로 부터 sampling한 후 , $a^{*} = argmax_{1 \leq k \leq K}\left \{X_t^TW_k \right \}$인, $a^{*}$를 선택하고 $r_{a^{*},t}$를 통해 posterior distribution을 update한다.
  • LinUCB : $LinUCB(\lambda)$을 통해 score가 가장큰 arm을 선택한다.
    
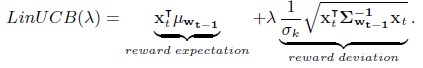
• 이러한 모델의 방법론을 dynamic context drift model에 적용시켰다.

3.2 Dynamic Context Drift Modeling

• arm $a^{(k)}$의 predicted reward는 contextual feature of $X_{t}$와 $W_k$의 linear combination으로 구해진다. 즉 $W_k$의 가중치들은 reward prediction을 하는데 영향을 준다.

• 기존의 방법론은 $W_k$ 가 distribution에 의해 정해진 가중치라고 생각하지만, Real-World에서는 distribution에 대해 알 수없기 때문에 context feature of $X_t$의 predicted reward는 dynamical하게 된다.

• 이에 저자는 dynamic 상황을 고려하여 시간에 따라 변화하는 reward에 대하여 $W_k$ 정보를 포착하기 위해 $W_{k,t}$를 t시점의 arm $a^{(k)}$의 가중치 벡터로 정의한다.
  

• $\delta_{W_{k,t}}$, 시간에 따라 변화하는 drift weight는 Contextual information의 다양한 특성, context feature의 다양한 scale 때문에 모델링하기 어렵다 (앞에서 설명한 동일한 context상에서의 CTR변화)

• 이에 저자는 추론을 간단화하기 위해 각각의 $\delta_{W_{k,t}}$를 독립적으로 변화한다고 가정한다.

• 불특정한 변환으로 인해 $\delta_{k,t}$를 scale variable $\theta_k$와 Gaussian random walk $\eta_{k,t}$의 element wise product로 표현한다.

• 이러한 모델은 실생활에서 변하는 reward를 고려하여 모델링하였다.

• 새로운 모델에서 $\text c_{\text w_{k}}$ 의 값들은 reward를 prediction하는 feature weight이고 $\theta_k$는 scale of context drifting을 의미한다. $\theta_k$의 값이 클수록 시간이 지남에 따라 feature에서 발생하는 context drifting을 의미한다.

4. Methodology and solution

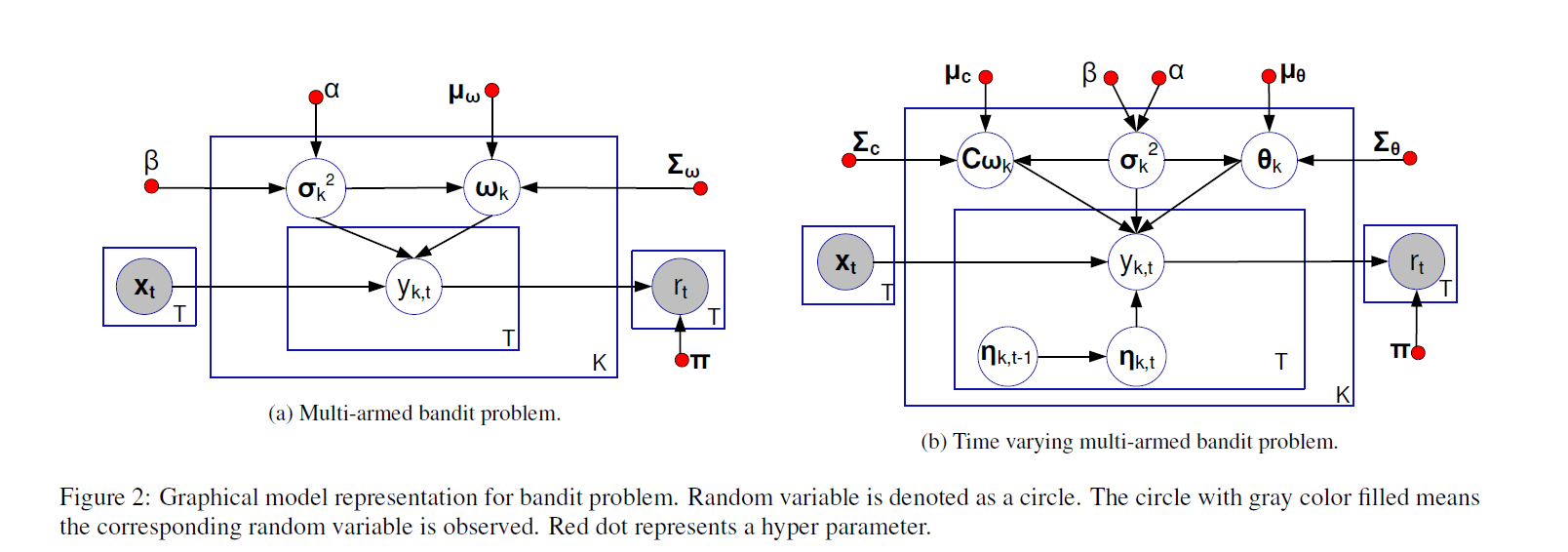
• Posterior distribution inference는 4개의 random한 변수들에 의해 정해진다. ($\sigma^2_k, \text c_{\text w_k}, \theta_k, \eta_{k,t}$)

• 이러한 4개의 변수들은 parameter random variable와 latent state random variable로 분류된다.

• $\sigma^2_k, \text c_{\text w_k}, \theta_k$는 고정된 parameter random variables고, 시간에 의존적이지 않다.

• $\eta_{k,t}$는 latent state random variable이고 시간에 의존적이다.

• t시점의 context $\text x_t$에 의해 arm $a^{(k)}$의 reward는 $r_{k,t}$로 구해지고 이러한 $X_t, r_{k,t}$는 random variables를 통해 확인될 수 있다.

• 모델의 목표는 latent parameters variables와 latent state random variables를 sequential observed data를 통해 추론하는 것이다. 하지만 latent state radnom variable은 random walk 방법에 의존하기 때문에, 저자는 latent parameters, latent state random의 distribution을 학습하기 위해 Sequential Monte Carlo sampling과 Particle learning을 이용하여 random walk 방법을 사용하였다.

  Standard gaussian random walk를 통한 state $\eta_{k,t-1}$은 시간에 따라 변화하기 때문에 이전 정보들을 통해 구해진 정보를 parameter로 하는 분포에서 뽑아 사용된다.
  $\eta_{k,t-1} \sim \mathcal N(\mu_{\eta_k},\sum_{\eta_k})$

4.1 Re-sample Particles with Weights

• t-1의 각각의 arm $a^{(k)}$는 고정된 particle size를 가지고 있다. Particle set을 $\mathcal P_{k,t-1}$, Particle set의 개수를 $p$로 생각하면 $\mathcal P^{(i)}_{k,t-1}$은 t-1시점의 arm $a^{(k)}$의 $i^{th}$ particle이 된다.

• 각각의 particle $\mathcal P^{(i)}_{k,t-1}$는 가중치가 있으며 이를 $\rho^{(i)}$로 표현하고 이는 t시점의 새로운 관측 데이터에 대한 적합도를 나타낸다. 즉, $\rho^{(i)}$는 이전 정보들을 통해 $\text x_t$와 t시점의 arm $a^{(k)}$의 reward의 likelihood로 정의된다.

• $y_{k,t}$ predicted value의 distribution은 $\sigma^2_k, \text c_{\text w_k}, \theta_k, \eta_{k,t}$ 를 통해 추정되기 때문에 $y_{k,t}= r_{k,t}$하에서 다음과 같이 $\rho^{(i)}$를 구할 수 있다.
  

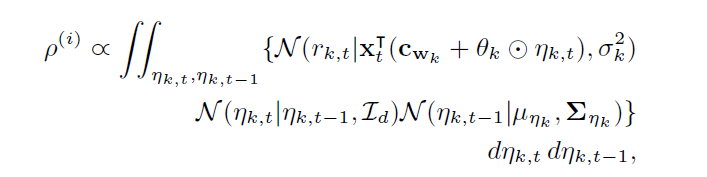
• parameter가 업데이트 되기 전에 resampling먼저 수행된다. weights of particles에 의해$\mathcal P_{k}$에서 generate된 $\mathcal P_{k}'$ 를 통해 sequential parameter가 업데이트 된다.

• 이러한 방식으로 weights of particles의 기반으로 보다 정확한 sampling이 가능해진다.

4.2 Latent State Inference

• t-1시점에서의 $\eta_{k,t-1}$의 충분 통계량은 $\mu_{\eta_k}$와 covariance $\sum_{\eta_k}$ 로 나타난다.

• t시점에서 새로운 $\text x_t$와 $r_{k,t}$이 발생되면 state $\eta_{k,t}$의 충분통계량은 다시 계산되어야 한다. 이때 kalman filtering method를 이용하여 재귀적으로 $\eta_{k,t}$의 충분 통계량을 update한다.
  

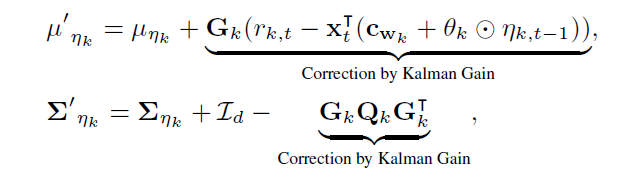
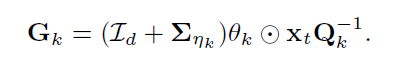
  Kalman Filter : 기존에 인지하고 있던 과거 측정데이터와 새로운 측정데이터를 사용하여 데이터에 포함된 노이즈를 제서키셔 새로운 결과를 추정하는데 사용하는 알고리즘으로 선형적 움직임을 갖는 대상을 재귀적으로 동작시킨다.

• 이를 통해 $\eta_{k,t}$는 다음과 같은 분포에서 추출된다.
  

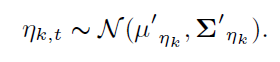
4.3 Parameter Inference

• t-1시점의 parameter random variable( $\sigma^2_k, \text c_{\text w_k}, \theta_k$)의 충분 통계량은($\alpha, \beta, \mu_c, \sum_c, \mu_{\theta}, \sum_{\theta}$)이다.
  
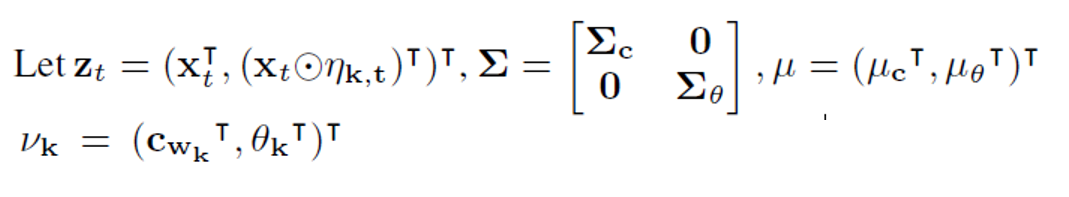
• $\text z_t, \mu, \nu$는 2d-dimensional vector이고 $\sum$은 2d x 2d - dimesional matrix 그러므로 $\text c_{\text w_k}$, $\theta_k$를 추론하는 것은 $\nu_k$를 추론하는 것과 같다.
  

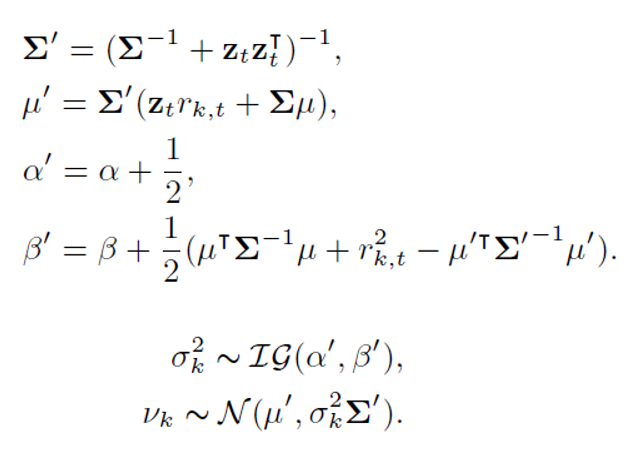
4.4 Intergration with Policies

• 3.1에서 LinUCB와 Tomson sampling은 $\text w_k, \sigma^2_k$가 posterior distribution에 의해 samplig된다.

• t 시점의 $\text x_t$에 대해서 arm $a^{(k)}$ 가 pulling되지 않았기 때문에 Context drifting model은 reward $r_{k,t}$를 모른다. 즉, t시점의 k번째 arm에 대한 reward가 없으면 t시점의 particle re-sampling, latent state inference, parameter inference가 samppling되지 않는다.

• 또한 모든 arm은 독립적인 p개의 particle을 가지고 있어서 각각의 particle에서 $\text w_{k,t-1}$의 posterior distribution을 이용할 수 없다. 왜냐면 현재까지 아는 정보는 $\text w_{k,t-2}$의 posterior distribution을 t-1시점의 prior distribution이 되기 때문이다.

• 이에 저자들은 Tompson smapling과 LinUCB가 weight sampling을 한 방법을 적용하여 다음과 같이 정의를 하였다.
  

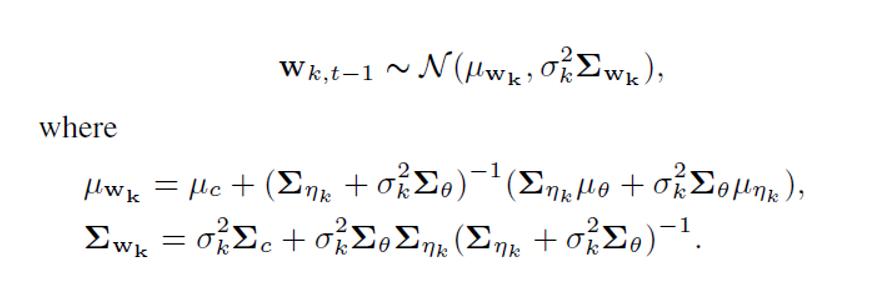
• $\text w^{(i)}_{k,t-1} , \mu^{(i)}_{\text w_k}, \sigma^{2^{(i)}}_k, \sum^{(i)}_{\text w_k}$를 $i^{(th)}$ particle의 random variables로 생각해보면 $\text w_{k,t-1}$을 $\bar{\text w}_{k,t-1}$로 정의할 수 있다. (bandit algorithm에서의 추론 방법)
  

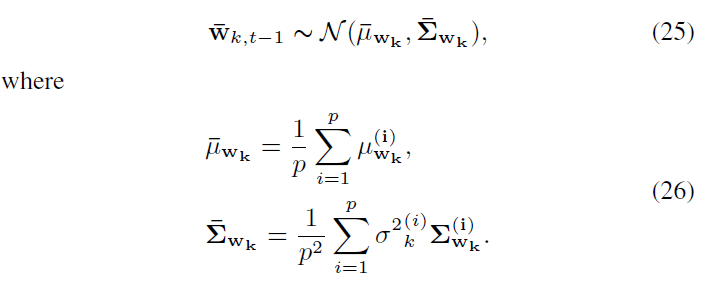
4.5 Algorithm

5.EMPIRICAL STUDY

• 저자는 모델을 성능을 확인하기 위해 2개의 real-world dataset을 사용하여 실험하였다. (the online search advertising data from Track2 of KDD CUP 2012, news recommendation data of Yahoo ! Today News)

5.1 Baseline Algorithms

• Random, $\epsilon-greedy$ , GenUCB($\lambda$), TS($q_0$), TSNR($q_0$), Bootstrap, Our Methods : TVUCB($\lambda$), TVTP($q_0$)

5.2 KDD Cup 2012 Online Advertising

• USER (age, gender)와 search engine(query keywords, some ads information about click count on ads)의 interaction 데이터

• 저자들은 binary feature vector of dimension 1,070,866 사용, 1 million user visit events

• Bandit problem evalution을 위해서는 simulation, replayer 방법이 있는데, large number of Recommending items (> 50) 에서는 simulation 방법이 적절 하였다.

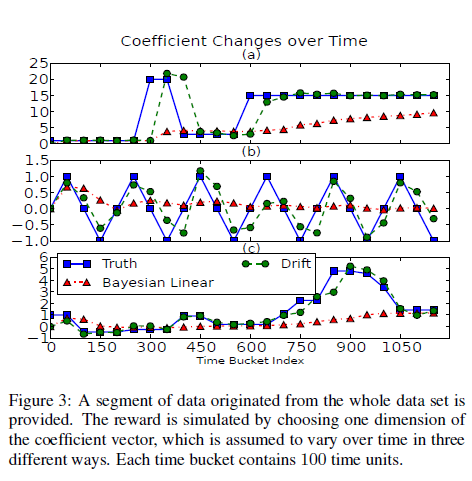
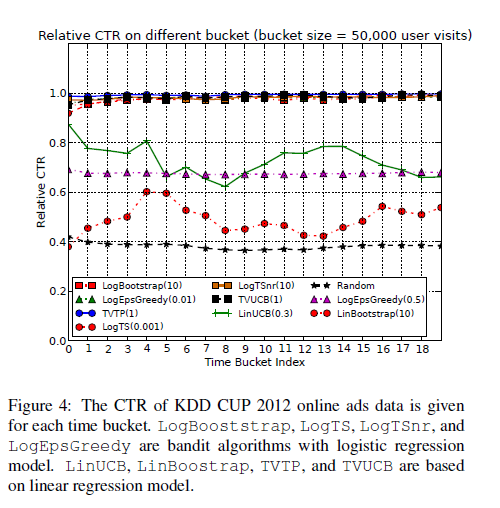
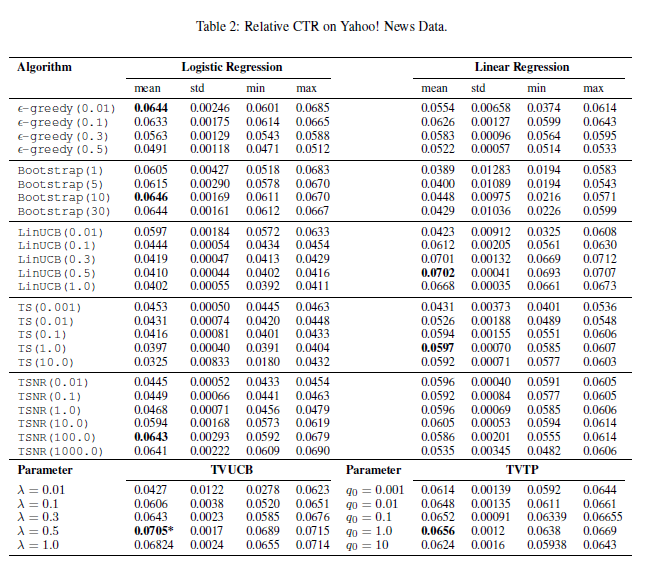
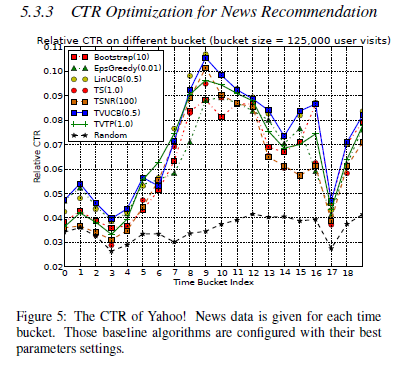
5.3 Yahoo ! Today News

• news data collection < 50 , replayer 방법 사용

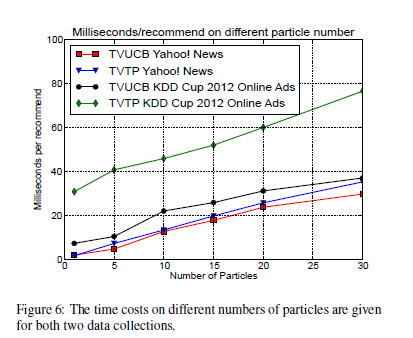
5.4 Time Cost

6. Conclusions

• 저자는 dynamic behavior of reward을 위한 context drift model을 제안하였다.

• Particle learning을 통해 parameters와 latent drift of the context을 효율적으로 학습하는 model을 제안하였다.

• 기존에 존재하는 Bandit algoritms를 개선하여 보다 contextual dynamics한 상황 tracking을 가능하게 하였으며 CTR에 대하여 personalized recommendation performance를 향상 시켰다.