[Paper Review] (2008, KDD) Factorization meets the neighborhood: a multifaceted collaborative filtering model
Recommender_System
작성자: 이원도
1. Introduction & Preliminary
Recommender System & Netflix Prize
추천시스템은 다양한 컨텐츠 중 유저가 마음에 들만한 것을 선별해 추천해주는 알고리즘입니다. 온라인 상품과 서비스가 넘쳐나기 시작하며 추천시스템의 중요성이 높아지고 있습니다.
2006년부터 2009년까지 진행된 Netflix Prize 대회는 추천시스템 알고리즘의 발전을 상징합니다. 본 논문의 저자 Koren 역시 Netflix Prize 대회에 참여해 1위를 달성했습니다.
이 논문은 이런 Netflix Prize가 진행되는 시기에 발표되었으며, 2000년대 ~ 2010년대에 유행한 추천시스템 알고리즘인 Collaborative Filtering을 종합적으로 정리합니다.
Collaborative Filtering
Collaborative Filtering은 2000년대 ~ 2010년대에 활발히 발달한 추천시스템 알고리즘입니다.
Collaborative Filtering의 두가지 주요 모델은 neighborhood based model과, latent factor model 입니다.
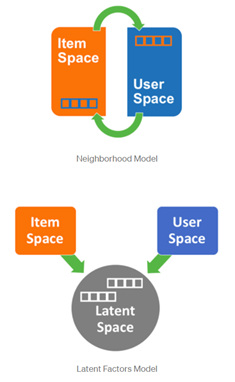
Neighborhood based model은 추천의 대상이 되는 user를 기준으로, item 소비 성향이 유사한 소수의 user의 데이터를 활용해 item을 추천합니다. user와 가장 가까운 소비성향의 이웃의 세부 데이터를 활용한다는 장점이 있지만, 반대로 모든 데이터가 아닌 일부 데이터만을 활용한다는 것이 단점입니다.
Latent Factor Model은 user와 item을 latent factor로 표현해 모델을 구성합니다. 전체 데이터를 활용해 latent factor를 구성하지만, neighborhood model의 세부적인 추천을 할 수 없습니다.
Explicit & Implicit Data
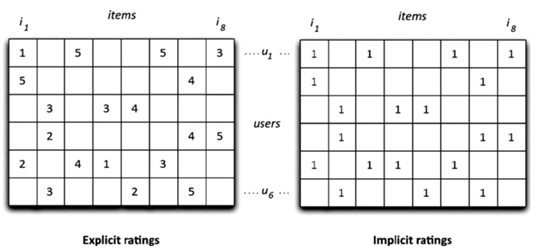
Collaborative Filtering에 주로 사용되는 데이터 형태는 user의 item에 대한 rating으로 구성된 Rating matrix입니다.
Rating matrix는 user의 item에 대한 선호 정보를 담고 있는 Explicit Data입니다.
Rating matrix를 user가 item을 소비했으면 1, 그렇지 않으면 0으로 이분화해서 표현한다면, 이는 Implicit Data가 됩니다. user가 item을 소비했다는 정보를 알 수 있지만 user의 item에 대한 선호를 알 수 없기 때문입니다.
Contribution
본 논문은 Neighborhood based Model, Latent Factor Model, Explicit Data, Implicit Data 를 모두 이용해 추천 모델을 만듭니다.
2. More on Neighborhood Model
Notation & Baseline Model
Notation
- user :
- item :
- rating :
Baseline Average Model estimates
Optimization
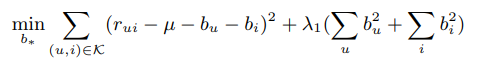
우선 특별한 알고리즘을 전혀 사용하지 않고 구성할 수 있는 모델은 user의 item에 대한 rating 를 전체 item의 rating 점수 평균 , user 의 점수 조정치 , item 의 점수 조정치 의 합으로 모델링 하는 것입니다. 는 해당 user(또는 item)이 평균 user에 비해 얼마나 평점점수를 후하거나 박하게 주는지를 조정하는 역할을 합니다. 이 baseline으로부터 시작해 모델을 점차 발전시킬 것입니다.
이 간단한 모델에서 최적화의 대상이 되는 파라미터는 이고, 최소화를 할 loss 함수는 위와 같습니다. 의 크기가 지나치게 커져 특정 값이 dominate하는 것을 방지하기 위해 의 제곱 크기에 비례하는 패널티를 준 것을 확인할 수 있습니다.
Basic Item-oriented Neighborhood Model
Model
가장 간단한 item-based neighborhood model은 다음과 같습니다.
에 대한 예측값은 baseline 예측값 에 추가로, user 가 점수를 매긴 아이템 중 item 와 가장 유사도가 높은 k 개의 아이템을 선택해, 이러한 k개의 item들에 대한 user의 평점의 가중평균값을 합친 것입니다. 이때 k개의 item의 가중평균에 사용된 각각의 가중치는 item 와 k개의 item 중 하나인 item 의 유사도 이며, 유사도 계산에 코사인 유사도, 피어슨 상관계수 등을 사용 할 수 있습니다.
이 방식은 의 계산에 item 와 유사한 item들의 평점을 활용했습니다. 대칭적으로 생각해 user 와 유사한 user들의 해당 아이템 에 대한 평점을 이용하는 방법도 생각할 수 있습니다. 하지만 '이 item과 유사한 item을 참고한 추천'이라는 개념은 직관적으로 와닿는 반면, '이 user와 유사한 user를 참고한 추천'은 user 사이의 유사성을 직관적으로 알기 쉽지 않다는 단점이 있습니다. 또한 성능적으로 item-neighbor 추천이 user-neighbor 추천보다 뛰어납니다.
논문의 저자 Koren은 basic neighborhood model의 추천 방법의 문제점과 보완법을 또 다른 논문에서 다뤘습니다. neighborhood model은 1)모든 이웃 정보가 아닌 소수의 정보만을 활용, 2)기준이 되는 item가 유사한 item이 없어도, 가중치 계산의 합이 1이 되기 때문에(i.e. ) 유사하지 않는 item이 왜곡된 영향을 줄 수 있다는 점, 3)user마다 rating한 item이 다르고 그에 따라 가중치의 계산이 번거롭다는 점 등입니다. 이중 일부 문제의 해결은 본 논문에서도 다뤄집니다.
Modify 1
Model
Basic Neighbor Model의 문제점은 user마다 top-k 유사한 item이 다르고 그에 따라 이웃의 평점을 추가할때 계산되는 가중치가 user마다 다르다는 것이었습니다.
Modify1 모델은 2개의 수정사항이 있습니다. 첫째로 계산되는 가중치가 로 바뀌었다는 것입니다. 이제 user마다 item 의 유사도의 가중합을 따로 계산할 필요 없이, 로 item 의 '관계'를 직접 계산한다는 것입니다. 이때 미묘한 부분은 은 코사인 유사도와 같은 수식적 유사도가 아닌, 최적화 과정에서 업데이트가 되는 파라미터라는 것입니다. 이전 모델에서 가 업데이트된 것과 차이가 있습니다. 둘째로 이전 모델에서 user마다 k개의 유사한 item 기준으로 계산을 한 것에 비해 이제 유저가 rating을 한 모든 아이템 를 계산 과정에 포함한다는 점이 있습니다. 이전 모델보다 넓은 데이터를 사용해 계산을 하는 것입니다.
Modify 2
Model
Modify2 모델은 user의 implicit 정보까지 모델에 추가합니다. 는 user가 소비한 item의 정보를 담고 있습니다. 1~5의 rating이 아닌 봤으면 1, 보지 않았으면 0의 정보를 담고 있습니다. 따라서 모델의 마지막에 추가된 항은 유저가 단순히 시청한 영화까지 고려하는 항이고, 는 이런 implicit 정보와 관련해 추가로 최적화 되어야할 파라미터입니다.
Modify 3
Model
Modify2 모델은 user가 rating한 item이 많아질수록, 예측치가 baseline 예측치 에서 멀어진다는 특징이 있습니다. 영화를 많이 본 heavy rater는 시청한 영화에 따라 더 많은 항들이 계산에 추가되고, 영화를 적게 본 user는 baseline 예측치에서 크게 벗어나지 않는 구조입니다.
Modify3 모델은 이렇게 rating 영화에 의해서 추가되는 항들의 크기를 조절하는 항을 포함했습니다. , 항이 그 기능을 합니다.
Modify 4
Model
Modify4 모델에서는 계산복잡도를 줄이고자 계산에 모든 neighbor item을 사용하지 않고 item 와 유사한 k개의 item 중 user가 소비한 item만을 계산에 사용하는 식으로 식을 조정했습니다. 유사하지 않은 item은 계산복잡도를 증가시키는 것에 비해 계산에 큰 영향을 주지 않기 때문입니다.
Final Neighborhood Model
Model
Optimization
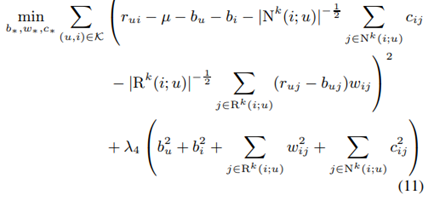
Modify4 모델이 basic neighbor model에서 최종적으로 향상시킨 모델입니다. 등의 파라미터가 업데이트 되는 것을 확인할 수 있습니다.
Performance
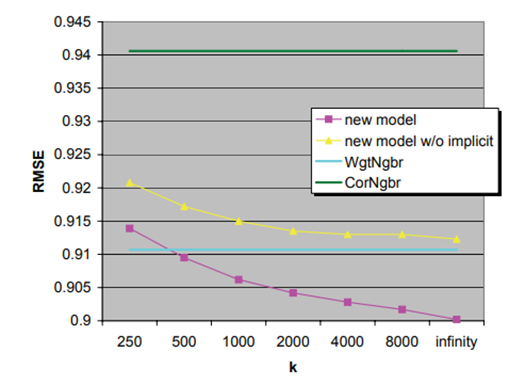
마지막의 Modify4 모델(new model)의 성능을 기본적 neighborhood model인 CorNgbr, WgtNgbr와 비교했습니다. 지표는 RMSE를 썼으며, RMSE 값이 작을수록 더 높은 성능을 의미합니다. 이웃의 개수 k가 많아질수록 new model의 성능이 향상됨을 확인할 수 있습니다. 또한 implicit data를 사용한 모델이 그렇지 않은 모델보다 성능이 좋은 것을 확인할 수 있습니다.
3. More on Latent Factor Model
Basic Latent Factor Model
Model
Optimization
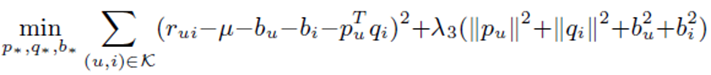
가장 간단한 latent factor model은 다음과 같습니다.
에 대한 예측값은 baseline 에 rating matrix 을 분해해 얻은 user 의 latent factor 와 item 의 latent factor 의 내적을 합한 값으로 구합니다. latent factor는 각각 d 차원의 벡터입니다.
등이 모델 적합과정에서 조정할 파라미터가 됩니다.
Paterek's Model
Model
Paterek이 제안한 모델이 참고로 소개됩니다. 는 item의 latent vector에 해당하는데, user의 latent vector를 구성하는 수식이 특이합니다. 는 item의 latent vector이며, user 의 latent vector는 user가 소비한 item 의 latent vector의 합으로 모델링됩니다. 마지막의 는 user가 소비한 item이 많을시 user vector의 크기가 지나치게 커지는 것을 방지합니다.
요점은 user가 소비한 item을 통해 user를 표현했다는 것입니다. 이 경우 장점은 다음과 같습니다. 첫째, user의 latent vector를 구성할 필요가 없기 때문에 파라미터를 절약할 수 있습니다. 새로운 user가 발생해도, user가 소비한 item의 latent vector를 이용해 별다른 추가 최적화 없이 추천을 해줄 수 있습니다. 둘째, user의 latent vector의 의미가 추상적일 수 있는데, user가 소비한 item을 이용해 user를 구성했다는 것은 직관적이고 설명력이 있습니다.
Modify1(Asymmetric SVD)
Model
Basic Latent Factor Model에서 수정한 모델은 다음과 같습니다. Paterek의 모델에 착안해 user의 latent vector를 user가 소비한 item들의 latent vector인 , 등을 이용해 구성한 것을 볼 수 있으며, 더 나아가 앞서 neighborhood model에서 살펴본 것과 같이 user의 item에 대한 explicit rating 정보와 implicit 정보까지 활용해 user의 latent vector를 계산한 것을 확인할 수 있습니다.
Modify2(SVD++)
Model
논문에서 Latent Factor Model 중 제일 성능이 좋은 구성으로 보고하는 모델입니다. 유저의 latent factor를 구성하는 부분에서 순수하게 유저에게 해당하는 latent factor인 를 다시 추가한 것을 확인할 수 있고, explicit rating 정보는 뺐지만 implicit item 정보는 사용했습니다. 여러개의 모델을 시도하고 최종적으로 성능이 좋은 모델로 선정한 것으로 보입니다.
Final
Model
Performance
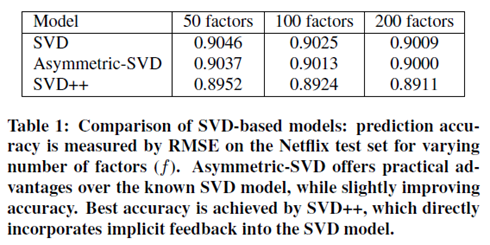
방금 살펴본 SVD++이 Latent Factor Model을 향상시킨 최종 모델입니다. Latent factor의 차원 수를 늘렸을때 성능이 향상되는 것을 확인할 수 있습니다.
4. Integrated Model
Model
Optimization

Performance

저자가 Integrated Model이라고 제안하는 최종 모델은 사실 neighborhood 모델과 latent factor model의 수식을 단순히 합한 것입니다. 관련한 파라미터는 그라디언트 디센트를 이용해 쉽게 최적화를 할 수 있으며 그 수식은 위와 같습니다. 성능 지표인 RMSE가 더욱 향상된 것을 확인 할 수 있습니다.
5. Result & Evaluation
Effect of RMSE improvement?
최종 모델의 RMSE가 0.8868로 보고되었습니다. Baseline 모델의 RMSE는 0.9514인데 불과 0.07의 RMSE 향상이 실제적인 추천에 영향을 미칠지 의문스러울 수 있습니다. 저자는 RMSE 향상이 실제 추천의 퀄리티를 향상시킨다는 것을, top-K evaluation이라는 또 다른 추천평가 지표를 사용해 보입니다.
Top K Evaluation
Top-k evaluation은 다음과 같은 방식으로 평가합니다.
-
Netflix dataset의 Test dataset에서, 특정 user가 5점 평점을 준 영화를 하나 고르고, 같은 user가 평점을 준 영화 중 5점을 받지 않은 1000개의 영화를 고릅니다.
-
학습된 추천 모델을 이용해 1001개의 영화에 대해 평점을 예측하게 하고, 예측된 평점이 높은 순으로 순위를 매깁니다. 이상적으로, 실제 user의 평점이 5점인 영화의 예측 평점이 높을 것이고, 다른 1000개의 영화보다 높은 순위를 가질 것입니다.
-
Test dataset의 를 만족하는 모든 384,573개의 평점에 대해 같은 과정을 반복합니다.
Result
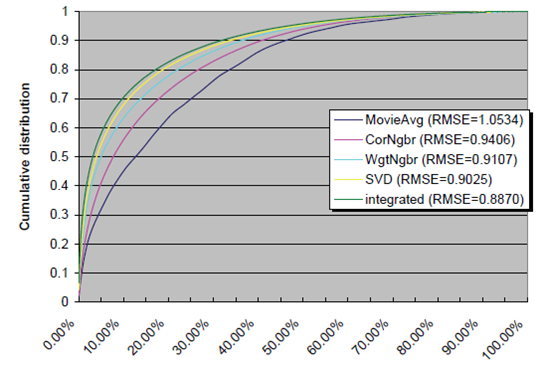
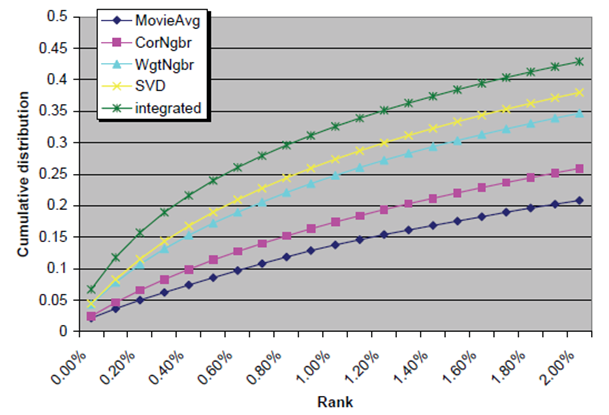
결과는 다음과 같습니다. x축은 순위의 100분율을 나타내며, y축은 누적된 item의 비율을 나타냅니다. 논문에서 제안된 초록색 integrated model은 다른 그래프와 비교해 가장 바깥쪽에 있는데, 이는 높은 순위를 매긴 5점 item의 비율이 높은 것을 의미하며 모델 성능의 우수함을 보여줍니다.
두번째 그래프는 첫번째 그래프에서 x축을 0%에서 100% 모두가 아닌 0%에서 2%만 나타내도록 확대한 그래프입니다. Item의 개수가 물리적으로 user에게 추천을 할 수 있는 item의 개수는 소수에 불과합니다. 따라서 평점 5점 item을 상위 30%, 나아가 상위 10%에 예측하는 것은 실질적 의미가 없습니다. 상위 2%, 상위 0.2%에 user가 선호하는 item을 정확히 맞추는 것이 실제 추천현장에서 의미가 있을 것입니다. 그래프를 확대해 보니, 0.00%에서 integrated model의 성능은 0.067로 0.05보다 확연히 위인 반면, 다른 비교모델은 0.05보다 아래인 것을 확인할 수 있습니다. 0.00%은 5점 item을 원래의 순위와 같이 1001개의 item 중 1위로 예측한 것을 의미합니다. 이렇듯 integrated model은 실제 추천에서 유의미한 추천 성능 향상을 가져옵니다.
7개의 댓글
Latent Factor Model은 Explicit Data 또는 Implicit Data 속에 존재하는 ? 부분을 추론하는 모델이다. 추론을 진행할 때 Latent Space를 활용하는데 이 Latent Space 자체가 무엇을 의미하는 feature인지 정확하게 정의할 수 없기 때문에 모델의 파라미터를 수정하는 방식과 구해진 target에 대한 설명력이 떨어질 수 밖에 없다.
하지만 본 논문은 Latent Factor Model과 유사도를 바탕으로 추천이 진행되는 Neighborhood Model을 결합하여 Latent Factor Model의 추론 과정을 유사한 유저 또는 컨텐츠를 활용하여 가중치를 주어 파리미터를 수정했고 이를 활용한 모델이 성능이 더 높다는 것으로 보아 target, 파라미터 수정 방식에 설명력이 조금 더 높아졌다고 말할 수 있으며 이 부분이 본 논문이 가져다주는 가장 큰 시사점이라고 생각한다.
개인적으로 본 논문은 Explicit Data와 Implicit Data 모두 사용하지만 두 데이터 모두 신규 영화 및 신규 유저에 대한 정보를 담기 어렵기 때문에 이에 대한 추천은 어렵다는 측면에서 추천시스템에서의 큰 이슈인 cold start 문제는 해결할 수 없다고 생각한다.
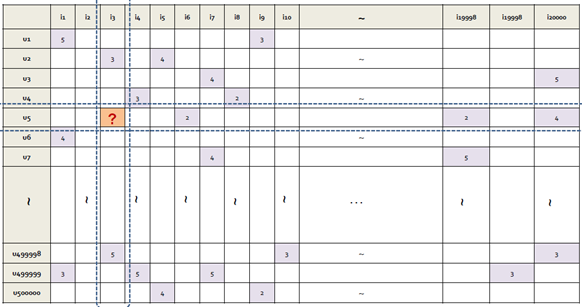
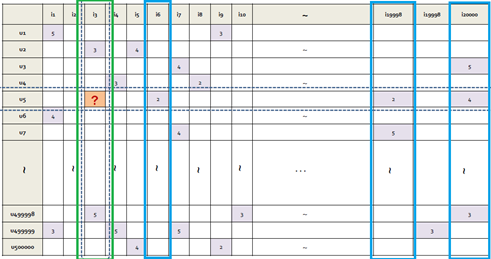
추천시스템을 구축할 때 우리의 목표는 유저 u가 소비하지 않은 아이템 i에 대한 평점 r_ui가 어떨지 예측하는 것이다.
우리가 이용할 수 있는 정보는 두가지이다. 유저가 아이템에 준 평점을 행과 열로 나타낸 explicit data, 유저가 아이템을 소비했는지 소비하지 않았는지만 알 수 있는 implicit data가 있다.
collaborative filtering 방식은 neighborhood model / latent factor model 로 나뉠 수 있다.
neighborhood model은 여러가지 모델이 있다.
neighborhood model: 아이템 i 와 유사한 상위 k개의 아이템의 평점의 가중평균(가중치는 유사도)
modify1: 아이템 i와 유저 u가 rating한 아이템(j)의 관계를 w_ij 로, 최적화되는 파라미터로 원래 모델의 유사도 대신 사용
modify2: modify1에 implicit data를 추가한 모델. 아이템 i와 유저 u가 소비한 아이템(j)의 관계를 c_ij로 나타내며, 학습되는 파라미터.
modify3: 소비한 아이템수가 많으면 baseline에 더해지는 값이 커져서 규제항을 더해준 모델
modify4: 아이템 i와 비슷한 상위 k개의 explicit data, implicit data 사용
latent model: 베이스라인 모델과 유저를 나타내는 행렬(p)에서 u의 벡터와 아이템을 나타내는 행렬(q)에서 i의 벡터의 곱으로 구성된다.
modify1: explicit data, implicit data에서 아이템의 latent vector를 사용해서 user의 latent vector를 형성한다.
modify2: 유저를 나타내는 행렬(p)의 u의 벡터와 implicit data를 사용해서 구성
최종모델인 intergrated model은 neighborhood model과 latent model의 합이다.
최종 모델 비교를 해보니, intergrated model 이 다른 모델에 비해 확연히 성능이 향상됨이 확인됌(Top K Evaluation)
neighborhood model과 latent model을 결합한 첫 시도를 했다는 점에서, Top K Evaluation을 고안해서 모델의 성능을 다각적으로 확인했다는 점에서 의의가 있는 논문이라고 생각한다.
[15기 김현지]
이 논문은 추천 시스템 알고리즘인 협업 필터링의 Neighbor factor model과 Neighborhood model을 합친 새로운 모델을 제시하였고, Explicit Data와 Implicit Data를 모두 사용하여 모델의 성능을 높였다.
Neighborhood Model
- item 기반 모델로, user 기반보다 개념이 직관적이며 더 뛰어난 성능을 기대할 수 있다.
- item 간 관계를 직접 계산하는 가중치()를 도입함으로써, 더 유연한 모델로 수정되었다.
- implicit data를 추가하여 시청 여부에 따른 영향력을 상쇄할 수 있게 되었으며, 성능 또한 향상되었다.
- 최종 모델에서는 계산복잡도를 줄이기 위해 모든 neighbor item이 아닌 item 와 유사한 개의 item 중 user가 소비한 item만을 계산에 사용하였다.
- 이웃의 개수 가 많아질 수록 성능이 향상되는 데, 계산비용이 증가됨을 고려하여 를 조절해야 할 것이다.
Latent Factor Model
1. Asymmetric SVD
- Paterek's model에 착안해 user의 latent vector를 user가 소비한 item들의 latent vector들을 이용해 구성하였다. 이때 explicit rating정보와 implicit 정보를 모두 활용하였다.
- 파라미터를 절약하고, 직관적이며 설명력이 있는 모델이다.
- SVD++
- user에게 해당하는 latent factor를 다시 추가하였고, explicit rating 정보는 뺐으며, implicit item 정보를 사용하였다.
- 논문에서 Latent Model 중 성능이 가장 좋은 모델로 선정었다.
⇒ SVD++모델의 예측 정확도가 더 높게 나왔지만 Asymmetric SVD의 장점 또한 매력적으로 보인다. 따라서 SVD++가 더 우수한 모델이라고 볼 수는 없을 거 같다.
An Integrated Model
- Neighborhood Model과 Latent Factor 모델을 합친 모델이다.
Evaluation
- RMSE 향상이 실제 추천의 퀄리티를 향상시킨다는 것과 top-k evaluation이라는 평가 지표를 제시하였다.
Neighborhood model과 latent model의 결합하여 새로운 모델을 제시하였고, explicit data와 implicit data를 모두 사용함으로써 더 다양한 정보를 활용할 수 있게 되었다는 점이 인상적이다.
[15기 장아연]
새로운 모델 제시 : Neighborhood model과 Latent factor model 합친 모델 제시
다양항 정보 활용으로 확장성 보임 : explicit/implicit feedback 모두 사용
<Neighborhood model +Latent factor model>
형식 : general properties + neigborhood + user/item간의 interaction
14기 박지은
본 논문에서는 neighborhood based model, latent factor model과 explicit data, implicit data를 모두 활용하여 모델을 만들었습니다. 먼저 neighborhood based model은 기본적으로 해당 유저가 평균 유저들에 비해 점수를 후하게 주는지 조정합니다. 그렇게 나온 가장 간단한 item based model은 해당 아이템과 유사한 아이템을 참고하여 추천하지만, 해당 유저와 다른 비슷한 유저 간의 유사성은 알기가 어렵습니다. 따라서 이웃의 평점을 추가할 때 계산되는 가중치를 아이템 간의 관계로 직접 계산하여 더 넓은 데이터를 이용해 계산하도록 했습니다. 또한 rating 영화에 의해 추가되는 항의 크기를 조절하였고, 유사한 아이템 중 소비한 아이템만 계산에 포함하여 연산량을 줄였습니다. 기본적인 모델을 조금씩 변형하고 결합하여 성능을 개선하는 점이 인상적이었습니다. 감사합니다!
본 논문은 추천시스템의 대표 알고리즘인 Collaborative Filtering의 두 주요 모델 Neighborhood based model과 Latent factor model을 수정하여 발전시킨 방법론들을 소개하고 있습니다. 각 baseline 모델에서 출발하여 수정된 주요 지점을 살펴보면,
우선 Neighborhood model의 경우
1. 가중치를 유사도가 아닌 학습될 파라미터로 변경하고 유저가 평가한 모든 아이템을 연산 과정에 포함합니다.
2. 아이템의 소비 여부를 나타내는 implicit 정보를 모델에 추가합니다.
3. 예측치의 값이 지나치게 벗어나지 않도록 조절하는 항을 추가합니다.
4. 계산복잡도를 줄이기 위해 유저가 소비하지 않은 아이템은 연산에서 제외합니다.
이어서 Latent factor model은
1. explicit과 implicit 정보를 모두 활용하고 유저가 소비한 아이템에 대한 정보로 latent vector를 구성합니다.
2. explicit 정보를 제외하고 유저에 해당하는 잠재 요인을 추가합니다.(SVD++)
이렇게 수정된 두 모델을 합하여 integrated model을 구축하여 RMSE을 줄인 효과를 볼 수 있었습니다. 또 다른 추천평가지표인 top-k evaluation을 도입하여 본 모델의 성능 향상을 증명했습니다.



Factor model과 neighborhood model을 사용자로부터 오는 명백한 피드백(explicit feedback)과 불명확한 피드백(implicit feedback)을 활용하도록 융합시켜서 정확도가 더 높은 모델이 만들어진다. 이 방법은 넷플릭스 데이터로 실험되었다. 또한, top-K recommendation task에 대한 성과에 기반한 새로운 평가 척도를 제안했다.
또한, https://velog.io/@superbunny38/Factorization-Meets-the-Neighborhood-a-Multifaceted-Collaborative-Filtering-Model-%EB%85%BC%EB%AC%B8-%EC%9A%94%EC%95%BD-%EB%B0%8F-%EA%B0%95%EC%9D%98-%EB%A6%AC%EB%B7%B0 에 엄청 자세하게.. 리뷰했습니답.. 흑흑..