작성자: 고려대학교 통계학과 김현지

Contents
1. Human language and word meaning
2. Word2vec introduction
3. Word2vec objective function gradients
4. Word2vec: More Details
5. Optimization basics

1. Human language and word meaning

How do we represent the meaning of a word?

어떻게 단어의 의미를 표현할까?

단어의 의미

우리의 말은 '문자'로 구성되며, 말의 의미는 '단어'로 구성된다. 단어는 말하자면 의미의 최소 단위인 셈이다. 그래서 자연어를 컴퓨터에게 이해시키는 데는 무엇보다 '단어의 의미'를 이해시키는 게 중요하다.

Human(Natural) Language

• 사람의 언어는 의미를 전달하기 위해 특별하게 구성된 시스템이다.
• 언어는 'sigdifier(symbol)'에 매핑된 'signified(idea or thing)'이다.

How do we have usable meaning in a computer?

컴퓨터에게 단어를 어떻게 표현할까?

시소러스 Thesaurus

: 유의어 사전으로, '뜻이 같은 단어(동의어)'나 뜻이 '비슷한 단어(유의어)'가 한 그룹으로 분류되어있다.

• 단어 사이의 '상위와 하위' 혹은 '전체와 부분' 등 더 세세한 관계까지 정의해둔 경우도 있다.

⇒ 이런 '단어 네트워크'를 이용해 컴퓨터에게 단어 사이의 관계를 가르칠 수 있다.

WordNet

: 자연어 처리 분야에서 가장 유명한 시소러스

시소러스의 문제점

1. 단어의 미묘한 차이를 표현할 수 없다.
   • 예를 들어 'proficient'와 'good'은 유의어로 묶이지만 뉘앙스가 다르다.
2. 신조어를 바로 반영하기 어렵다.
3. 단어가 주관적이다.
4. 단어와 단어 간의 유사도(similarity)를 계산할 수 없다.

Representing words as discrete symbols

단어를 discrete symbols로 나타내기

전통적인 NLP에서는 단어를 discrete symbols로 간주한다.

One-hot vector

• 벡터의 원소 중 하나만 1이고 나머지는 모두 0인 벡터
• 벡터의 차원 = vocabulary의 단어 수
  - vocabulary의 단어 수가 많아지면 sparse 해지며, 차원이 커진다.
• 각 단어의 유사도를 계산할 수 없다.

Example: 웹 검색을 할 때 사용자는 "Seattle motel"을 검색하면 "Seattle hotel"이 포함된 문서도 찾아지길 원한다.
그러나

이 두 벡터는 orthogonal하다.

• one-hot vecotor에서 유사도에 대한 자연스러운 개념은 없다.

Representing words by their context

맥락으로 단어 표현하기

• 단어의 분산 표현은 단어를 고정 길이의 밀집 벡터(dense vector)로 표현한다.
• 밀집 벡터는 대부분의 원소가 0이 아닌 실수인 벡터를 말한다.

분포가설 Distributional Semantics

: 단어의 의미는 주변 단어에 의해 형성된다.

• 단어 $w$가 텍스트에 나타날 때, 그 맥락(context)는 근처(고정 크기 window 내)에 나타나는 단어 집합이다.
• 동일한 맥락(context)에서 사용되는 단어는 비슷한 의미를 가지는 경향이 있다.
• 단어 $w$의 맥락(context)를 사용하여 $w$의 표현을 작성한다.
  

Word Vectors

: 우리는 각 단어에 대해 밀집 벡터(dense vector)를 만든다. 이는 유사한 맥락(context)에서 나타나는 단어들끼리 유사하게 구성된다.

• word embeddings 혹은 word representations으로 불린다.
  

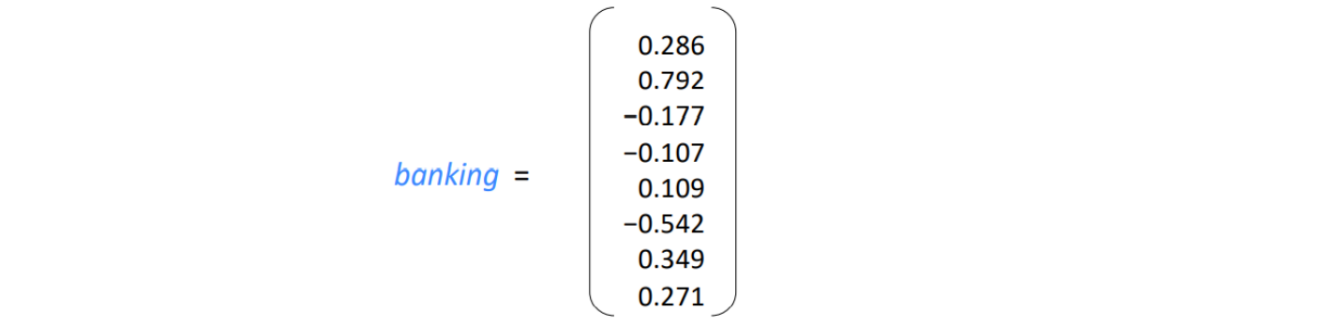
Word meaning as a neural word vector: Visualization

---

2. Word2Vec Introduction

Word2Vec Overview

추론 기반 기법

• 추론이란 아래 그림처럼 중심 단어(center word)가 주어졌을 때, 주변 맥락에 무슨 단어가 들어가는지를 추측하는 작업이다.

➡ 이러한 추론 문제를 반복해서 풀면서 단어의 출현 패턴을 학습한다.

Word2Vec

: word vectors를 학습하는 프레임워크

Idea

• 우리는 많은 텍스트 말뭉치(corpus)를 가지고 있다.
• 고정된 vocabulary의 모든 단어는 벡터로 표현된다.
• 위치 $t$의 텍스트는 중심 단어(center word) $c$와 맥락 단어(context word) $o$를 가진다.
• $c$와 $o$에 대한 word vectors의 유사도를 이용해 $c$가 주어졌을 때 $o$가 나타날 확률을 계산한다.
• 이 확률을 최대화하기 위해 word vectors를 계속 조정해나간다.

Example windows and process for computing $P(w_{t+j}|w_t)$

Word2Vec의 추론 처리

✅ 중심 단어(center word)로부터 맥락 단어(context word)를 추측하는 용도의 신경망을 사용한다.
→ 이 모델이 가능한 정확하게 추론하도록 훈련시켜서 분산 표현을 얻어낸다.

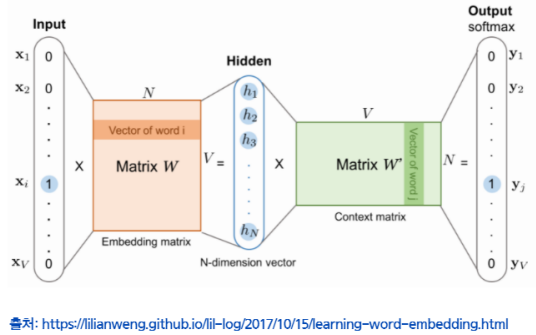
• 모델의 입력은 중심 단어(center word)이다.
  - 이 중심 단어를 원핫 벡터로 변환하여 모델이 처리할 수 있도록 준비한다.
• 입력층이 은닉층을 거쳐 출력층에 도달한다.
• 입력층에서 은닉층으로의 변환은 완전연결계층이 처리한다.
  - 은닉층의 뉴런은 입력층의 완전연결계층에 의해 변환된 값이다.
• 출력층의 뉴런은 총 $V$개 인데, 이 뉴런 하나하나가 각각 단어에 대응한다.
  - 출력층의 값은 각 단어가 맥락 단어로 나타날 확률을 뜻한다.
  

입력층에서 은닉층로의 변환은 matrix $W$에 의해 이루어진다. 이 가중치 $W$의 각 행에는 해당 단어의 분산 표현이 담겨 있다. 학습을 진행할수록 맥락에서 출현하는 단어를 잘 추측하는 방향으로 분산표현들이 갱신된다. 놀랍게도 이렇게 얻은 벡터에는 '단어의 의미'도 잘 녹아있다.

Word2Vec: Prediction Function

• 중심 단어(center word) $c$와 맥락 단어(context word) $o$에 대해:
  -$v_w$ when $w$ is a center word
  -$u_w$ when $w$ is a context word
  

$P(o|c)={\exp(u_o^Tv_c) \over \sum_{w \in V}\exp(u_w^Tv_C)}$

Softmax function: $\mathbb{R}^n \rightarrow \mathbb{R}^n$의 예시
$softmax(x_i)={\exp(x_i) \over \sum_{j=1}^n\exp(x_j)}=p_i$

• $x_i$는 출력측 완전연결계층 후의 각 단어에 대한 점수
  - 이 값이 높을수록 대응 단어의 출현 확률도 높아진다.
• 분자: 점수 $x_i$의 지수 함수
• 분모: 모든 값들의 지수 함수의 총합
• softmax function의 출력의 각 원소는 0.0이상 1.0이하`

Word2Vec 예측 함수

• 두 단어 벡터에 대한 내적을 통해 유사도를 계산 → 대응 단어가 출현할 정도로 해석 가능

Word2Vec: Objective Function

Word2Vec 목적함수

Likelihood

• 각 위치 $t=1,...,T$에서 중심 단어(center word) $w_j$가 주어졌을 때, 크기 $m$으로 고정된 윈도우 안의 맥락 단어(context word) 예측할 때

Objective function (cost or loss function)

목적 함수 $J(\theta)$는 (average) negative log likelihood이다.

➡ 이 obective function을 최소화해야 한다.

Training a model by optimizing parameters

• 모델을 학습하기 위해, 손실(loss)을 최소화하도록 파라미터를 조정한다.
  E.g. below, for a simple convex function over two parameters Contour lines show levels of objective function

To train the model: Compute all vector gradients!

Optimization을 통해 objective function을 최소화하는 파라미터 $\theta$, 즉 $u$와 $v$(word를 나타내는 두 벡터)를 찾는다.

• $\theta$는 모델의 모든 파라미터를 하나의 긴 벡터로 나타낸다.
• $V$개의 단어가 존재하고 $\theta$가 $d$-dimension vector일 때, word vector는 $u, v$를 포함하므로 $2dV$ 차원을 갖는다.
• 기울기(gradient)를 따라가면서 이 파라미터들을 최적화한다.

---

3. Word2Vec objective function gradients

Word2Vec derivation of gradient

• Uselful basics: ${\partial x^Ta \over \partial x} = {\partial a^Tx \over \partial x} =a$

Chain Rule

If $y=f(u)$ and $u=g(x)$, i.e $y=f(g(x))$, then:

Simple example:
${\operatorname{d}\!y\over\operatorname{d}\!x}={\operatorname{d} \over\operatorname{d}\!x}5(x^3+7)^4$

• $y=f(u)=5u^4$
  : ${\operatorname{d}\!y\over\operatorname{d}\!x}=20u^3$
• $u=g(x)=x^3+7$
  : ${\operatorname{d}\!u\over\operatorname{d}\!x}=3x^2$

⇒ ${\operatorname{d}\!y\over\operatorname{d}\!x}=20(x^3+7)^3 \cdot 3x^2$

✔ 참고

로그 함수 미분

$y=\ln f(X)$ 일 때, $y'={1 \over f(x)}\cdot f'(x)$

지수 함수 미분

$y=\exp(f(x))$ 일 때, $y'=\exp((f(x))\cdot f'(x)$

기울기 유도

Objective funcion:

• 목적함수를 최소화하기 위해

이 식을 중심 단어(center word), 맥락 단어(context word)로 각각 미분한다.

미분 과정

이처럼 objective function을 편미분한 것은 실제 단어와 예측한 단어와의 차이와 같다. 따라서 gradient descent를 통해 실제에 더 가깝게 예측할 수 있다.

---

4. Word2Vec: More Details

Why two vectors?
➡ Easier optimization. Average both at the end

Two model variants

1. Skip-grams (SG): 중심 단어(center word)가 주어졌을 때, 맥락/주변 단어(context/outside words)를 예측한다.
2. Continuous Bag of Words (CBOW): 맥락 단어(context words)들로부터 중심 단어(center word)를 예측한다.

Additional eifficiency in training

• Negative sampling

---

5. Optimization basics

Optimization: Gradient Descent

Gradient Desent

• 우리는 최소화하고 싶은 비용함수 $J(\theta)$를 가지고 있다.

• Gradient Descent는 $J(\theta)$를 최소화하는 알고리즘이다.

• Idea: for current value of $\theta$, calculate gradient of $J(\theta)$, then take small step in direction of negative gradient. Repeat.
  

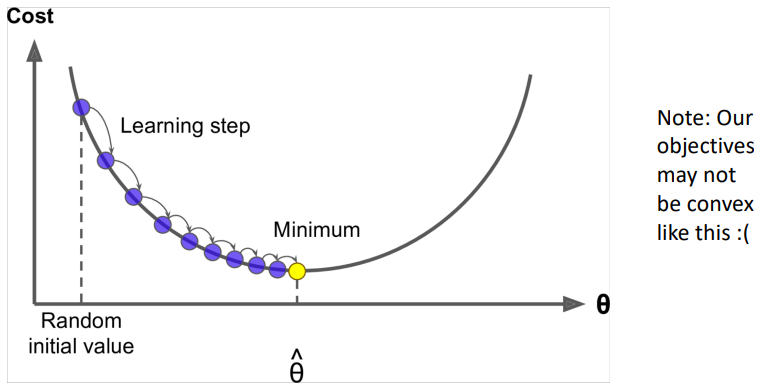
• Update equation (in matrix notation):
  

• Update equation (for single parameter):
  

• Algorithm:

While True:
    theta_grad = evaluate_gradient(J, corpus, theta)
    theta = theta - alpha * theta_grad

Stochastic Gradient Descnet

Problem:

$J(\theta)$는 corpus의 모든 windows에 대한 함수이다.
🚨 수십억개가 될 수도 있다!

• 그래서 $\nabla_\theta J(\theta)$의 계산 비용이 매우 비싸다.

Solution: Stochastic gradient descent

모든 windows 대신 sample window 단위로 update한다.

• 전체 data를 가지고 한 번의 loss function을 계산하는게 아니라 batch 단위로 loss function을 계산

Algorithm:

While True:
    window = sample_window(corpus)
    theta_grad = evaluate_gradient(J, window, theta)
    theta = theta - alpha * theta_grad

---

Stanford CS224N: NLP with Deep Learning | Winter 2019

Reference

• CS224N: NLP with Deep Learning | Winter 2019 | Lecture 1 강의 자료
• 밑바닥부터 시작하는 딥러닝 2 | 사이토 고키 (한빛 미디어)

투빅스 15&16기 텍스트 세미나 발표자료

• Lecture 1: Introduction and Word Vectors (15기 김현지)