Week 02 | Generative Adversarial Network
이번 tobigs 16-17기 GAN은 카이스트 강남우 교수님 강의와 나동빈님 코드를 많이 참고해 작성했습니다!
0. Prerequisite
이전 주차 기수분들이 잘 설명해주셨지만, GAN을 수식적으로 받아들이기 위해서는 확률분포 및 likelihood, expectation에 대한 기초적인 이해 및 아래의 term에 대한 이해가 필요합니다.
0.1 KL-Divergence
정보이론 & Entropy
KL-Divergence를 이해하기 위해서는 정보이론에 대한 사전지식이 필요합니다. 따라서 간단히 설명을 해보겠습니다.
통계학에서는 놀랄만한 내용일수록 정보량이 많다고 표현한다고 합니다.
이를 확률의 개념에서 다시 이해를 해보면, 확률이 낮은 사건일 수 정보량은 높다고 할 수 있죠.
왜냐하면 그 사건은 거의 일어나지 않을 일이기 때문입니다. 이를 수식으로 표현해보면 아래와 같습니다. 정보량
정보량 =
Entropy는 어떤 샘플 공간에서의 정보량에 대한 기닷값을 의미하는데,
기댓값의 성질에 따라 이산 확률변수의 경우에는 아래와 같이 정의될 수 있습니다. 인 샘플 공간이고, 는 정보량을 의미한다.
.
본격적으로 KL-Divergence에 대해서 다루어보겠습니다.
KL-Divergence는 동일한 샘플 공간에서 정의되는 두 함수의 차이를 측정하는 지표입니다.
우리가 근사하고자하는 분포를 , 어떤 최적화 방법으로 모델링한 분포를 라고 할 때
KL-Divergence의 수식을 살펴보면 아래와 같이 정의됩니다.
KL-Divergence는 우리가 근사하고자하는 분포를 의 entropy term과 와 의 cross entropy로 분해되는 것을 알 수 있습니다. 저는 이 부분을 두 확률분포의 차이는 기준으로 두는 확률분포가 자제척으로 가지는 정보량과 두 확률분포의 차이에 의해서 발생하는 정보량으로 정의가 되는 것으로 이해했습니다.
어쨌든, KL-Divergence는 내가 어떤 확률분포를 타겟으로 두느냐에 따라 그 값이 달라 지게됩니다.
다시 말해, 인것이죠. 따라서 KL-Divergence는 차이를 평가할 수 있는 척도로는 활용할 수 있지만, 거리라는 척도로는 활용하지 못합니다.
0.2 Jenson Shenon Distance
KL-Divergence의 한계를 극복하기 위해 고안된 지표가 Jenson Shenon Distance입니다.
0.3 Game Theory
다들 아시는 것처럼 GAN은 Generator와 Discriminator라는 2개의 모듈이 Game-Thoery에 근간을 두고 최적화를 진행합니다. 즉 Discriminator는 Generator의 결과를 알고 있으며, 그것을 바탕으로 최적화를 진행합니다. Discriminator 최적화 이후 Generator 역시 Discriminator의 결과를 알고 그 결과를 바탕으로 최적화를 진행합니다.
K-means와 Gaussian Mixture Model을 최적화 하기 위해 쓰이는 Expectation-Maximization 알고리즘을 떠올려보시면 이해가 빠를 듯합니다.
1. Introduction
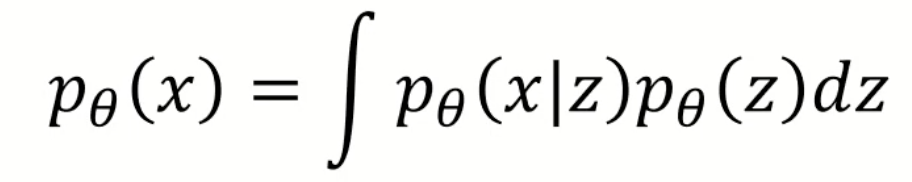
지난 시간에 살펴본 VAE는 data의 likelihood를 maximization하기 위해서 다음과 같은 목적함수를 두었으나. 의 분자 term이 marginalize하는게 사실상 불가능했습니다. 이를 해결하기 위해 posterior 를 계산하려 해도 여전히 불가능했기 때문에, Encoder 를 활용해 분포를 근사하는 변분추론 기법을 활용하였습니다.
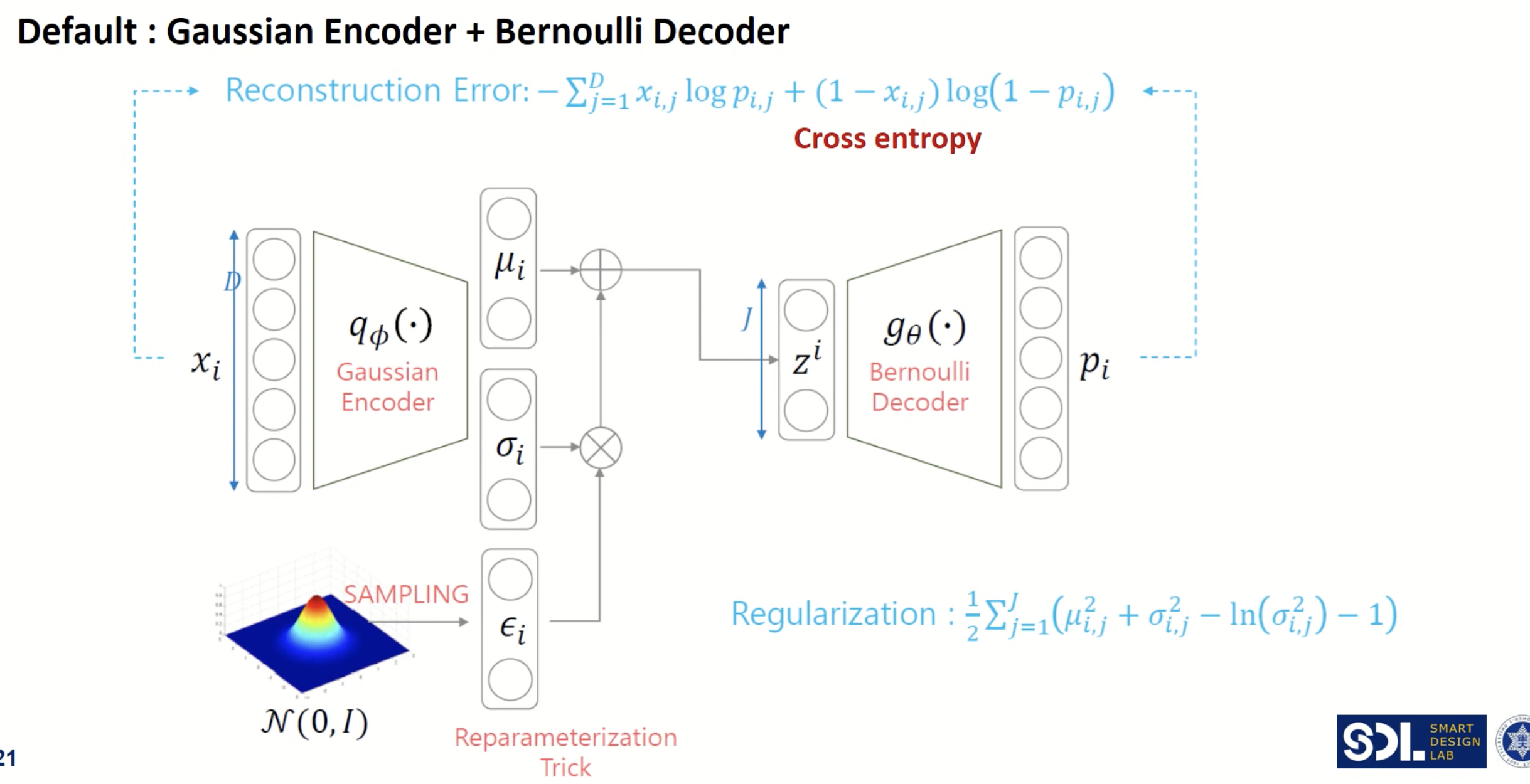
따라서 VAE는 결국 수리적으로 data의 likelihood를 maximization하기 위해 계산된 수식에서 ELBO를 최대로 올려서 원래 데이터의 분포를 최대한 근사시켰죠.
하지만 과연 원래 분포를 제대로 근사시키기는게 가장 좋은 방법일까요?
이 문제를 해결하기 위해(해결하기 위해 쓴거는 아니겠지만?) GAN은 특정 분포나 markov chain과 같은 가정 없이 latent space에서 잘 sampling되어서 나온 후 잘 생성이 되도록 하는 구조를 제안합니다.
2. GAN Structure
2.1 Structure
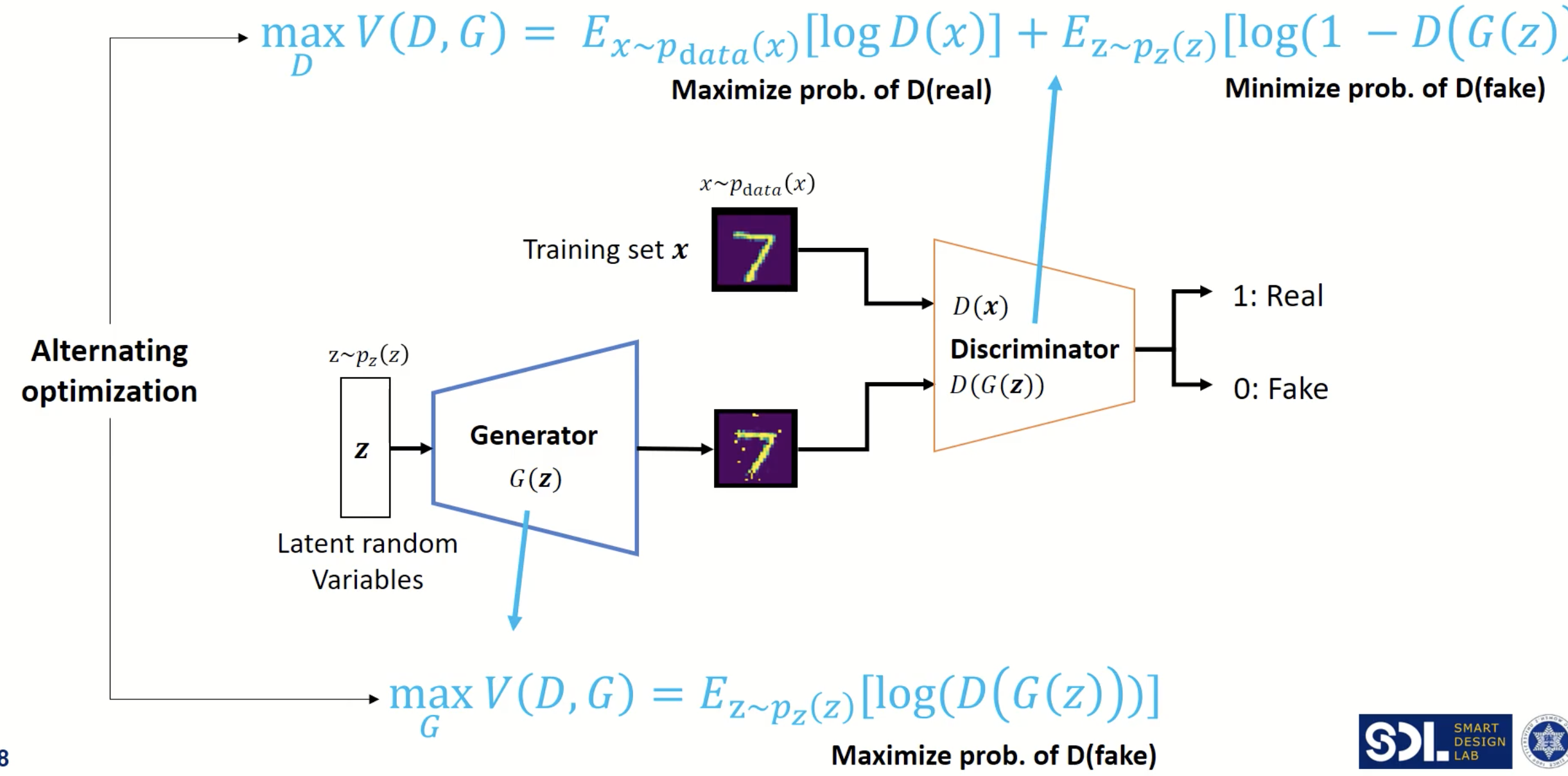
Vanilla GAN은 MLP로 이루어진 Generator와 Discriminator로 이루어져 있습니다. Generator는 가정한 사전 확률분포에서 sampling한 latent vector를 원래 image에 맞게 복원하는 역할을 하고, Discriminator는 Generator가 latent vector로부터 reconstruct한 image는 가짜로, 기존에 있던 이미지는 진짜로 분류하는 역할을 합니다. 사전에 설명드린것처럼 game theoric approach에 의해 Generator와 Discriminator가 반복적으로 학습을 안정적으로 진행하면, Generator에서 생성된 이미지의 분포와 원래 데이터의 분포가 같게 되고, Discriminator는 그 둘을 구별하기 어렵게 됩니다. GAN의 구조는 아래와 같습니다.
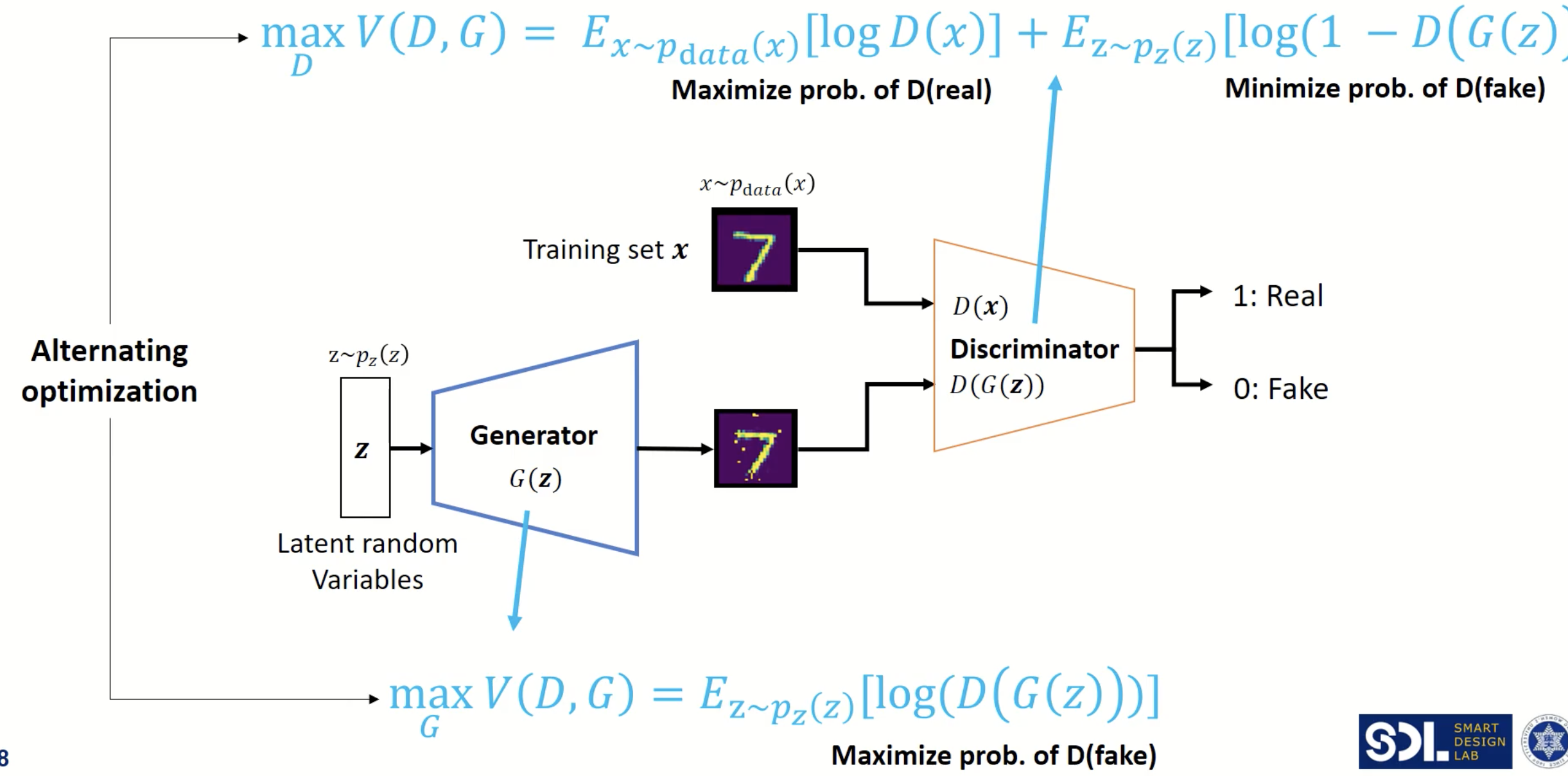
우선 GAN의 학습 과정에 대해서 간략하게 설명하면,
- Latent vector space를 가우시안 분포로 가정하고 z를 하나 샘플링 합니다.
- 샘플링된 z를 Generator에 태워서 가짜 이미지를 만듭니다. (=G(z))
- 원래 데이터 붙포에서 추출된 x는 진짜 레이블인 1을, g(z)에는 가짜 레이블이 0을 주어 Discriminator를 학습합니다.
- Back-propagation에 의해 gradient를 업데이트 합니다. (실제 학습과정은 아래에서 보다 더 구체적으로 설명드리겠습니다.)
이를 그림으로 보면 아래와 같습니다.
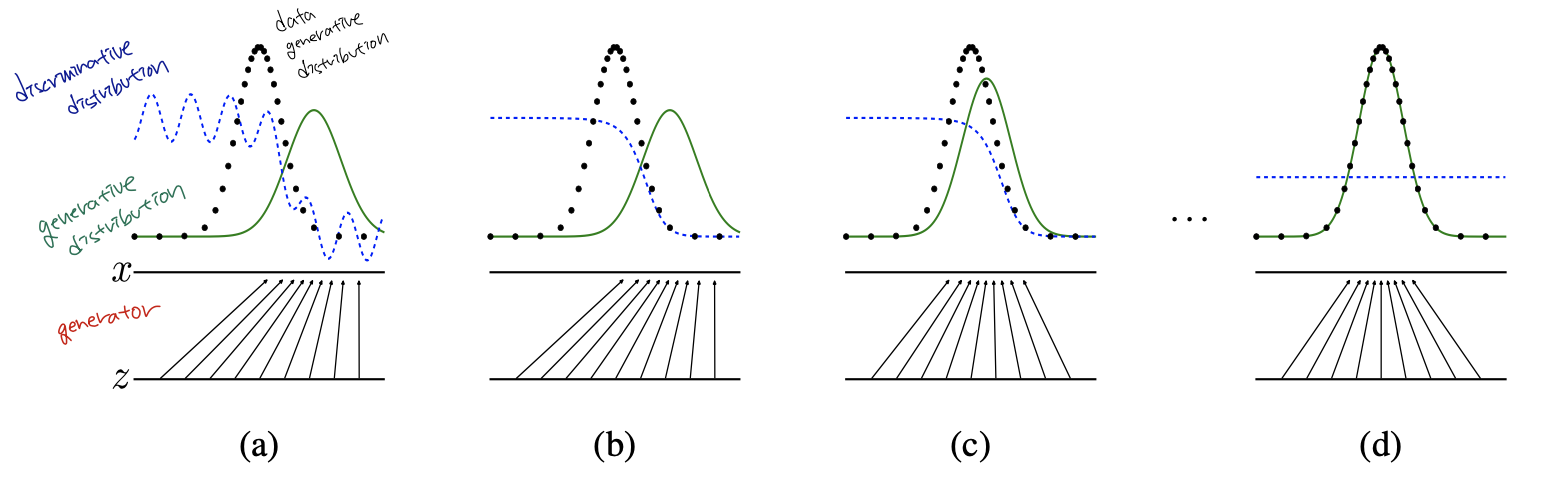
처음에 Generator가 생성한 이미지의 분포가 skewed 되어 있어 (=이미지를 제대로 생성하지 못해서) Discriminator가 각 영역에서 분류를 정확히 하고 있습니다. 하지만 학습이 진행됨에 따라 점점 2개의 분포가 같아지고, Discriminator는 두 분포를 전혀 구분하지 못하게 됩니다.
2.2 Objective Function
GAN의 목적함수는 아래와 같습니다.
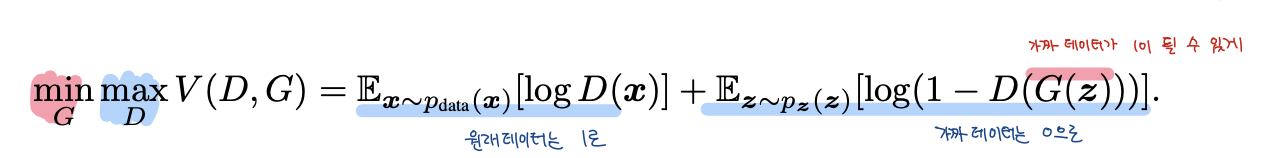
Discriminator는 목적함수를 최대화하도록 훈련을 하고, Generator는 목적함수가 최소가 되도록 훈련합니다. 저자들은 Discriminator를 한 epoch에 대해서 먼저 훈련을 하고 Generator를 학습하면 overfitting이 된다고 지적하면서, Discriminator를 K step, Generator를 1 step으로 번갈아가면서 훈련을 진행했다고 합니다. Discriminator를 더 많이 훈련한 이유는 Discriminator가 성능이 최적해 근처에 있어야 Generator가 천천히 update하면서 더 이미지를 그럴듯하게 만들 수 있어서라고 합니다.
2.2.1 Discriminator 학습
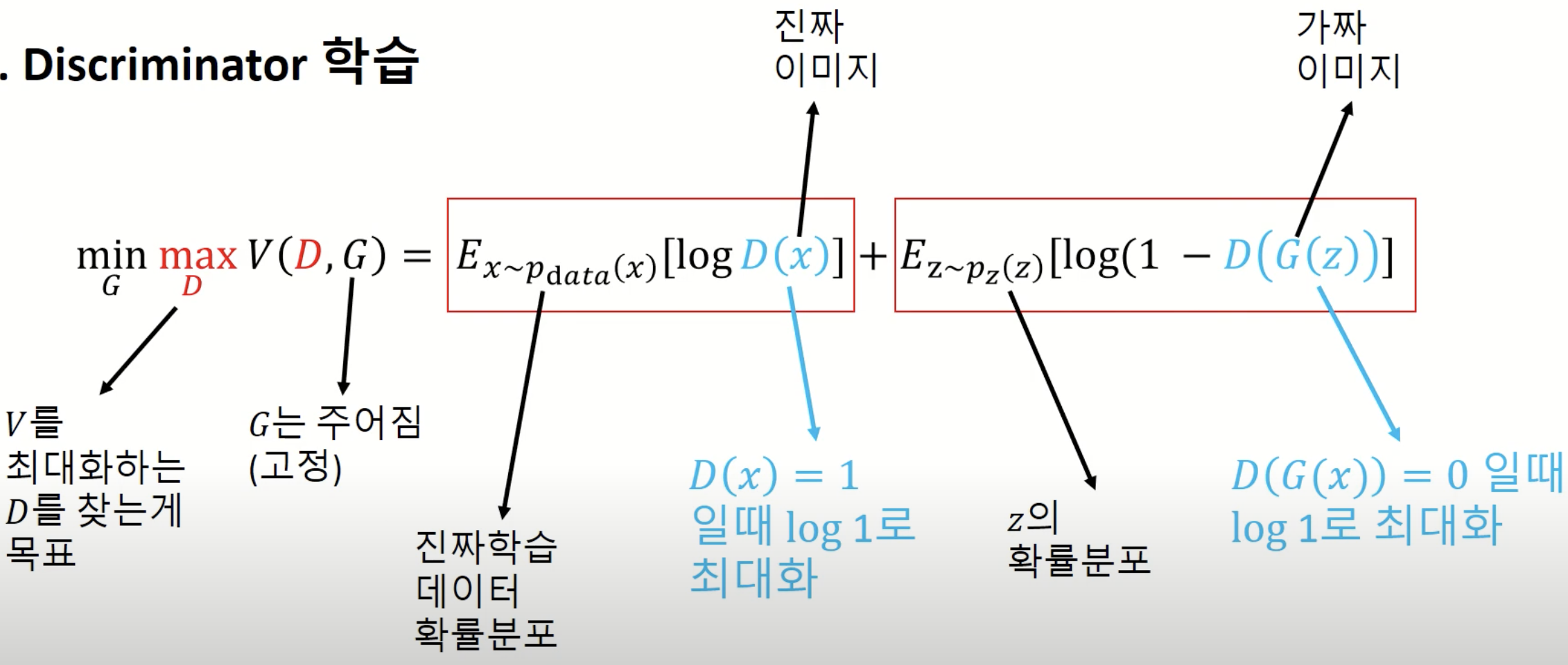
Discriminator 학습시에는 목적함수의 2가지 term을 둘다 활용합니다. 진짜 이미지일 경우에는 를 1에 가깝게, Generator일 경우에는 를 0에 가깝게 훈련하면 목적함수가 최대화되는 것을 쉽게 확인할 수 있습니다.
2.2.2 Generator 학습

Generator 학습 시에는 2번째 term만 활용합니다. 저자들은 보다 원활한 수렴을 위해서 목적함수를 변경합니다. 그 이유는 처음에 Generator가 생성하는 이미지의 퀄리티는 좋지 않기 때문에 은 0에 가까울 것이고 이는 목적함수에서 의 위치에 있는데 위의 그림의 우하단을 보면 해당 위치에서 기울기가 작은 것을 확인할 수 있습니다. 따라서 처음에 Generator가 학습을 원할하게 하기 위해 목적함수를 로 바꾸어줍니다. 이렇게 되면 높은 확률로 Generator가 초반에 더 큰 gradient로 원활할 학습을 할 수 있게 되겠죠.
3. Proof
이번 절에서는 왜 Generator가 생성한 이미지 분포인 와 원래 이미지 분포인 가 같을 때 GAN의 목적함수의 최적해인지에 대해서 알아보겠습니다.
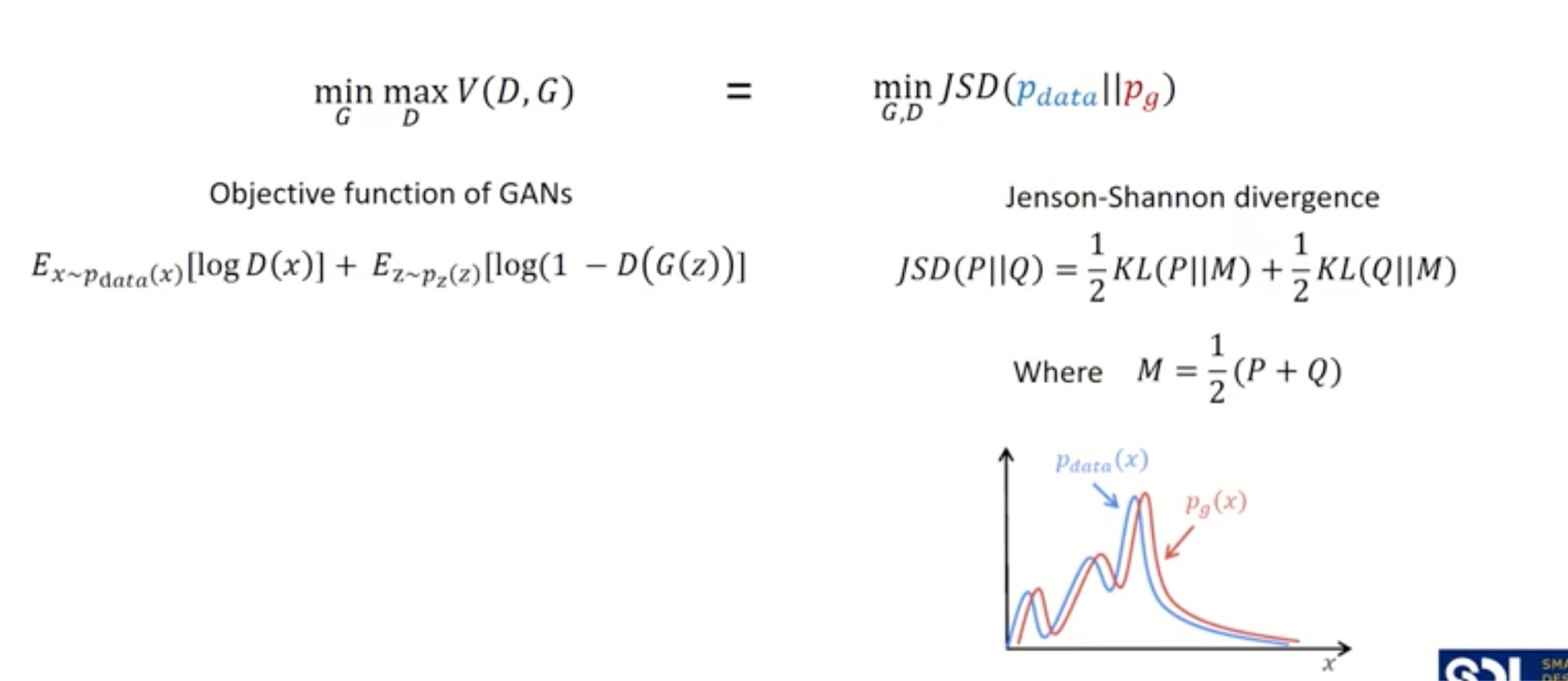
우선 와 원래 이미지 분포인 가 같다는 것은 두 분포 사이의 거리를 나타내는 측도인 가 최소화 되는 것과 동일한 의미입니다.
먼저 Discriminator부터 최적화해보겠습니다.
Generator는 고정된 상태에서 최적 Discriminator는 목적함수를 최대화시키는 파라미터를 가지고 있습니다.


위의 2 슬라이드를 따라가보면, 최적 Discriminator는 * 로 원래 이미지 분포와 Generator가 생성한 이미지 분포 중 원래 이미지 분포를 잘 선택하는 상태입니다.
Min-Max game theoric approach에 따라 최적 상태인 Discriminator를 고정하고 Generator를 최적하면 우리가 원했던 목표인 가 도출되어야 합니다.
아래 증명을 따라가보죠.

즉, 와 원래 이미지 분포인 가 같아야 Generator가 최적화된 것이며, 이는
Discriminator 입장에서는 * 인 상태를 의미합니다. 다시 말해, 두 분포가 같으면 최적화된 discriminator는 두 분포를 구별하지 못한다는 것을 의미하죠.
4. Training Algorithm

저자들은 K=1로 두어 실제로는 discriminator와 generator가 한번씩 번갈아가면서 학습했다고 합니다. 또한 목적함수가 convex해서 수렴할 수 밖에 없다고 증명을 해놓았던데, 제가 수학적으로 많이 부족해 그 부분을 이해하지 못했습니다..
또한 저자들은 위 구조로는 generator로 근사한 분포가 목표로 하고자하는 분포를 표현하는데 한계가 있어 generator의 파라미터를 업데이트하는 식으로 훈련을 진행했고, generator로는 다양한 임계점을 갖는 파라미터 공간을 가진 MLP를 선택했다고 합니다.
5. Experiments

저자들이 논문에 제시한 GAN이 생성한 이미지는 위와 같습니다. 각 section의 맨 오른쪽 column은 training set에서 바로 각각 생성된 이미지의 nearest sample이라고 합니다. 이를 통해 cherry-picking을 하지 않았는데도 (당시 기준으로) 괜찮은 이미지들이 많이 생긴 것을 확인할 수 있습니다.
GAN은 VAE에 비해 보다 Sharp한 이미지를 만들 수 있다는 장점이 있습니다.
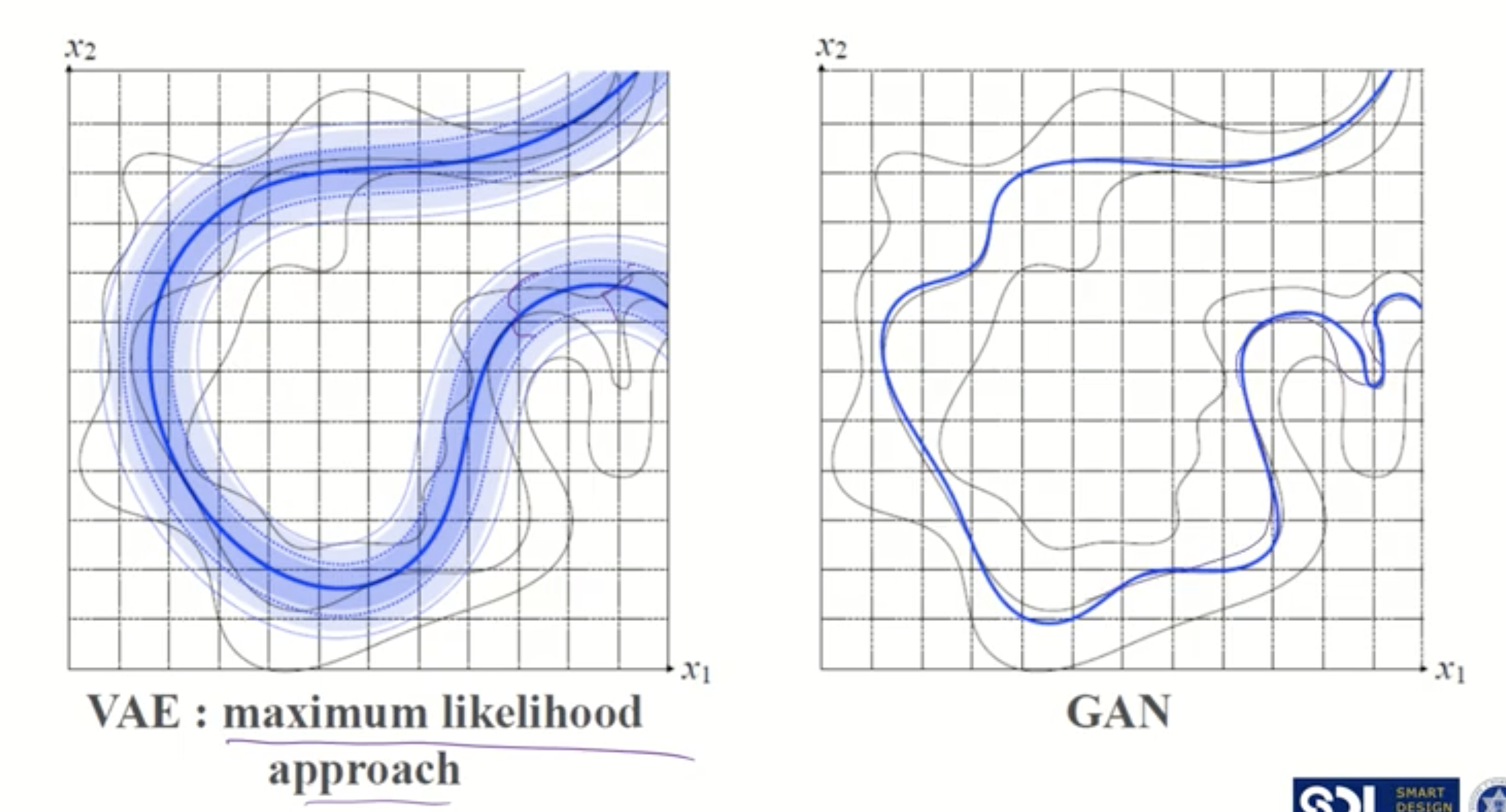
VAE는 분포를 가정하고 수리적으로 그 분포를 근사시키는 decoder를 학습하는 모델이기 때문에 전반적인 이미지는 잘 만들어내나 (분포를 어느정도 비슷하게 수렴시키나) , 원래 이미지를 세세하게 복원하지는 못합니다. 하지만 GAN은 Discriminator를 속이기만 하면 되기 때문에 보지 못한 이미지를 Sharp하게 만들 수 있으나, 잘 생성이 되는 vector space에서 조금만 벗어나면 잘못된 이미지를 생성하는 (분포의 다양성을 무시하고 mode에만 최적화 되어버리는 문제) mode collapse 문제가 있다고 합니다.

또한 GAN 자체는 Min-Max Game Theory를 바탕으로 학습되기 때문에 수렴이 어렵다고 합니다. 위의 mode collapse 문제 때문에 MNIST에서 숫자 하나만 생성하는 경우가 많은 것도 그 중 하나입니다.
이를 해결하기 위해서는 아래와 같은 3가지 방법이 있다고 합니다.
- feature matching : 가짜 데이터와 실제 데이터 사이의 least square error를 목적함수에 추가
- mini-batch discrimination : 미니배치별로 가짜 데이터와 실제 데이터 사이의 거리 합의 차이를 목적함수에 추가
- historical averaging : 배치 단위로 파라메터를 업데이트하면 이전 학습은 잘 잊히게 되므로, 이전 학습 내용을 기억하는 방식으로 학습
Code
Discriminator & Generator 정의

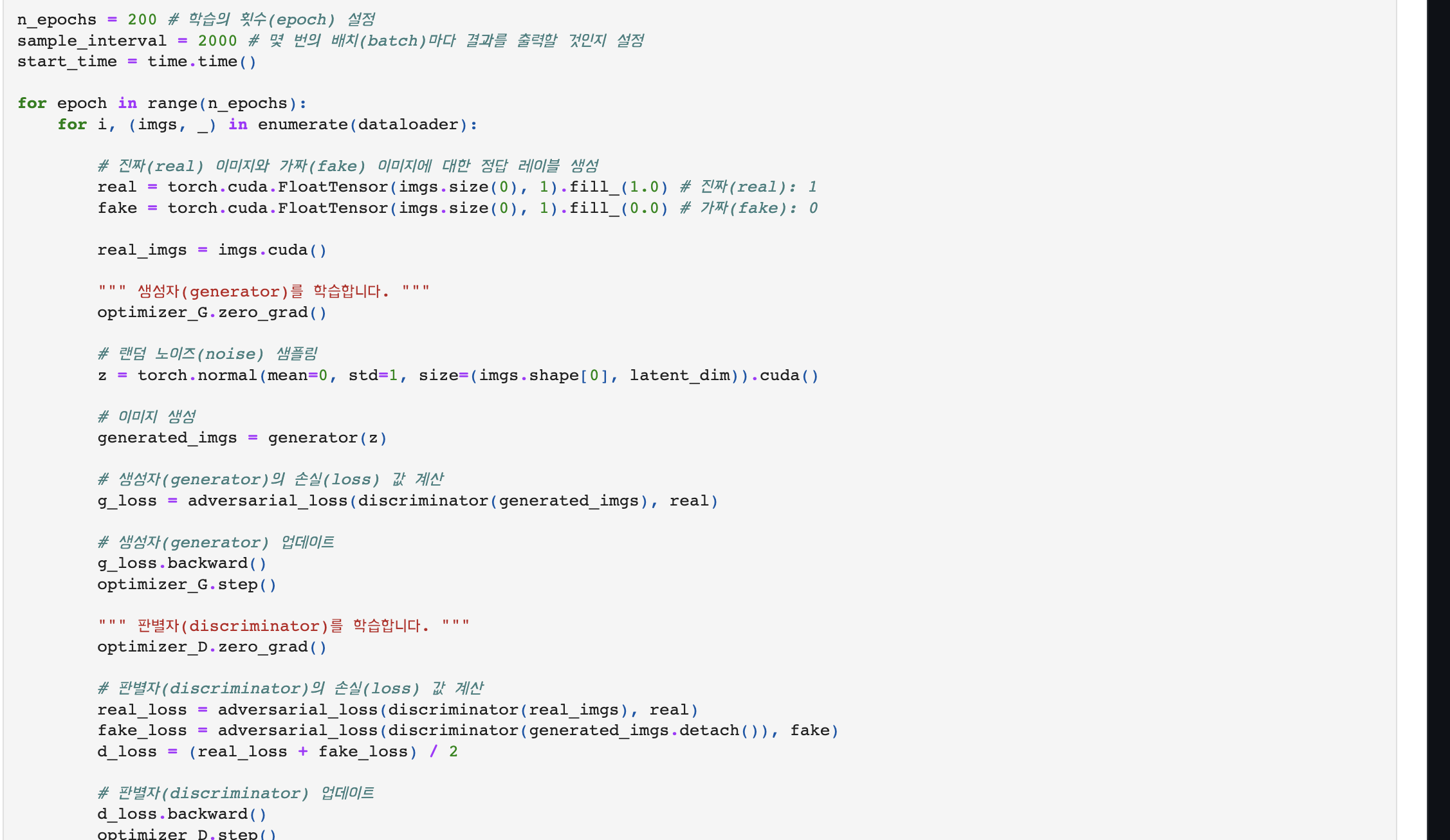
학습과정
Reference
공돌이님의 수학정리노트-KLDivergence
DeepLearning AI GAN 1강
나동빈님 코드
나동빈님 강의
강남우 교수님 강의
pseudo-lab
Ratsgo님 GAN Post
Tobigs 1516 GAN Post
