WGAN-GP, GAN 평가

WGAN-GP

(1) introduction

$W(\mathbb{P}_r, \mathbb{P}_g) = \inf_{\gamma \in \Pi (\mathbb{P}_r, \mathbb{P}_g)} \mathbb{E}_{(x, y) \sim \gamma} \left [ \lVert x - y \rVert \right ]$'

WGAN은 KL-divergence와 JS-divergence metric의 단점을 W-distance를 이용함으로써 해결했다.(판별자가 먼저 학습이 완료 되어도 유의미한 gradient를 만들 수 있기 때문에 생성자의 학습이 가능하다. 원 논문에서는 판별자 5회- 생성자 1회 학습 진행) 그러나 수식의 계산이 힘들다는 단점이 존재했다. (x,y)쌍은 단순 샘플링을 통해서 해결할 수 있지만, $\Pi (\mathbb{P}_r, \mathbb{P}_g)$ (marginaldl Pr, Pg인 모든 결합 분포의 집합)을 모두 탐색하긴 어려울 것이다.

$W(\mathbb{P}_r, \mathbb{P}_g) = \sup_{||f||_L \le 1} \mathbb{E}_{x \sim \mathbb{P}_r} [f(x)] - \mathbb{E}_{x \sim \mathbb{P}_\theta} [f(x)]$

그래서 Kantorovich-Rubinstein Duality Theorem
을 통해 이 문제를 1-Lipshitz 함수를 이용해 표현 가능하도록 만들었다. 따라서 이 조건을 만족하는 optimal한 함수 f를 찾을 수 있다면, W-distance를 구할 수 있게 된다.

이제 이를 loss로 활용하기 위해 형태를 바꾸어 주면 다음과 같다.

$W(\mathbb{P}_r, \mathbb{P}_g) = \min_g\max_{w \in \mathcal{W}} \mathbb{E}_{x \sim \mathbb{P}_r} [f_w(x)] - \mathbb{E}_{x \sim \mathbb{P}_\theta} [f_w(g_\theta(z))]$

discriminator($f_w(x)$)에 대해서 W-distance를 최대화 하고, generator에 대해서는 최소화한다. 생성자의 loss에 해당하는 부분은 아래와 같이 표현 된다.

$L^{(g)} = - \mathbb{E}_{x \sim \mathbb{P}_\theta} [f_w(g_\theta(z))]$

WGAN은 지속적으로 가중치 w를 업데이트 함으로써 함수 f를 원하는 목적에 맞춰 근사시킨다. 그러나 W distance를 위와 같은 방식으로 사용하기 위해선 1-Lipshitz 조건을 만족해야 하는데, 이를 기존 WGAN의 경우, weight clipping 기법을 사용했다. 하지만 이러한 방식은 분명, 문제점이 존재하며 저자들은 grdient penalty term을 이용한 WGAN-GP를 제안하여 문제를 해결하고자 한다.

(2) Gradient Penalty

WGAN은 함수 f를 학습 목적에 맞춰 근사 시키는데, 1-Lipshitz 조건을 만족시키기 위해 weight clipping을 사용했다. WGAN-GP는 weight clipping의 해결책으로 Gradient Penalty를 제시했다.(GP)

먼저 이를 위해서 WGAN loss의 optimal한 f의 특성을 알아야한다.

$f^* = \arg \max_{||f||_L \le 1} \mathbb{E}_{y \sim \mathbb{P}_r} [f(y)] - \mathbb{E}_{x \sim \mathbb{P}_g} [f(x)]$

판별자 f의 입장에서 optimal한 f는 1-Lipshitz 조건을 만족하면서 loss식을 최대화 하는 것이다.
x는 generator에서 생성된 값을 sampling한 것이고, y는 real data에서 sampling한 것이다.

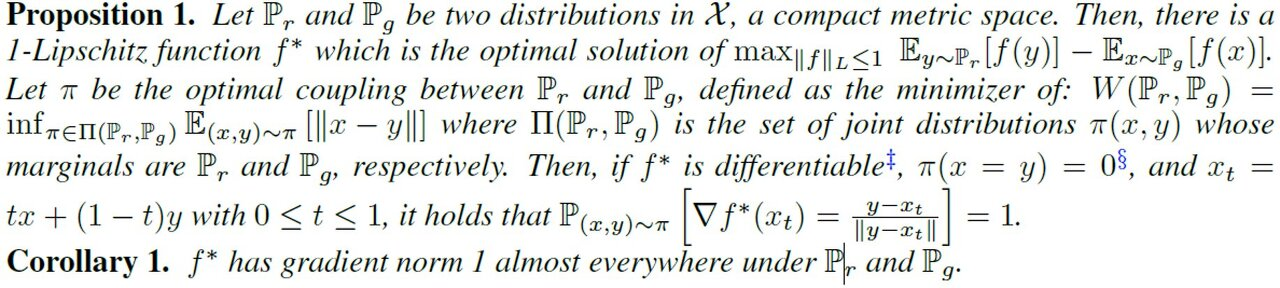
위의 정리에 따르면 최적해 $f^*$에 대해서 x,y로 sampling한 두 점의 내분점($x_t$) 아무곳에서나

$||\nabla f^* (x_t)|| = 1$

위 조건을 만족한다고한다. 따라서 이러한 조건을 loss에 term으로 추가하면 다음과 같은 형태가 된다.

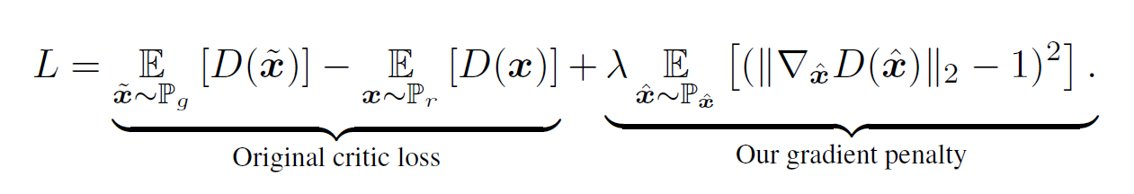
$\hat{x}$는 생성이미지와 실제이미지를 sampling하여 보간한 직선 상에서 uniform 하게 sampling한다.

(3) Comparison and Experiments

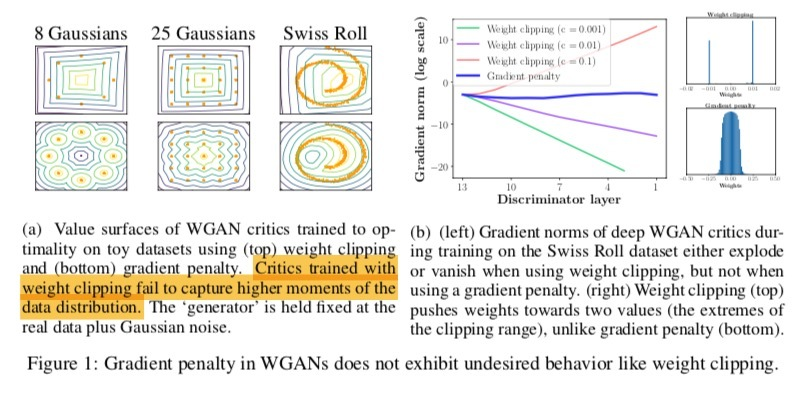
toy dataset에 대하여 GP방식과 weight clipping 방식을 비교해 보았다.(a) 위는 weight clipping, 아래는 gp방식이다. weight clipping의 경우 data 분포의 higher moment를 탐지하는데 어려움을 보이고 있다.

또한 swiss roll dataset에 대하여 판별자의 깊이와 weight clipping의 범위를 달리하여 gradient의 norm을 계산한 결과, gp는 어떤 경우에서도 안정적인 반면, weight clipping은 gradient가 안정적이지 못한 모습이다. 또한, weight의 분포 역시 양쪽으로 치우쳤다.

그리고 기존 WGAN의 loss의 경우 adam optimizer를 사용하면 불안정하다는 결과가 있어, rmsprop을 사용했는데, WGAN-GP의 경우 adam optimizer도 사용 가능하게 되었다.

아래는 다양한 구조에서 여러 GAN모델을 학습시킨 결과이다. WGAN-GP는 실험된 모든 구조에서 안정적으로 학습이 진행되었다.(LSUN)

WGAN, WGAN-GP의 LOSS 설명

WGAN, WGAN-GP

---

GAN 평가

(1) IS (Inception Score)

IS는 GAN의 성능 측정을 위해서 두 가지 기준을 고려한다.

• 생성된 이미지의 quality
• diversity (이미지 다양성)

이를 측정하기 위해서 pre-trained된 Inception-v3 모델을 분류기로서 사용한다.

생성된 이미지를 Inception 모델에 통과시키면 분류 class에 대한 확률 분포 값이 나타난다.

이미지의 quality가 좋다면, 이미지가 정해진 라벨대로 잘 분류 될 것이고, 그런 경우 확률 분포의 엔트로피는 낮게 나타날 것이다.(분포의 분산이 작다.)

marginal 분포란, 생성된 이미지 분포의 sample들의 class에 대한 분포를 합산한 것으로, 다양한 이미지가 나타났다면 이 분포의 엔트로피는 높게 나타날 것이다.(분포의 분산이 크다.)

모든 출력은 확률분포이기에 이러한 비교는 쉽게 이루어질 수 있다.
두 분포의 KL-divergence를 계산하여 차이가 크면 클수록 높은 점수를 부여한 것이 Inception Score이다.

수식은 다음과 같다.

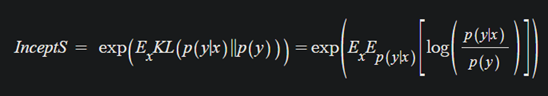
y: label
x: 생성된 이미지

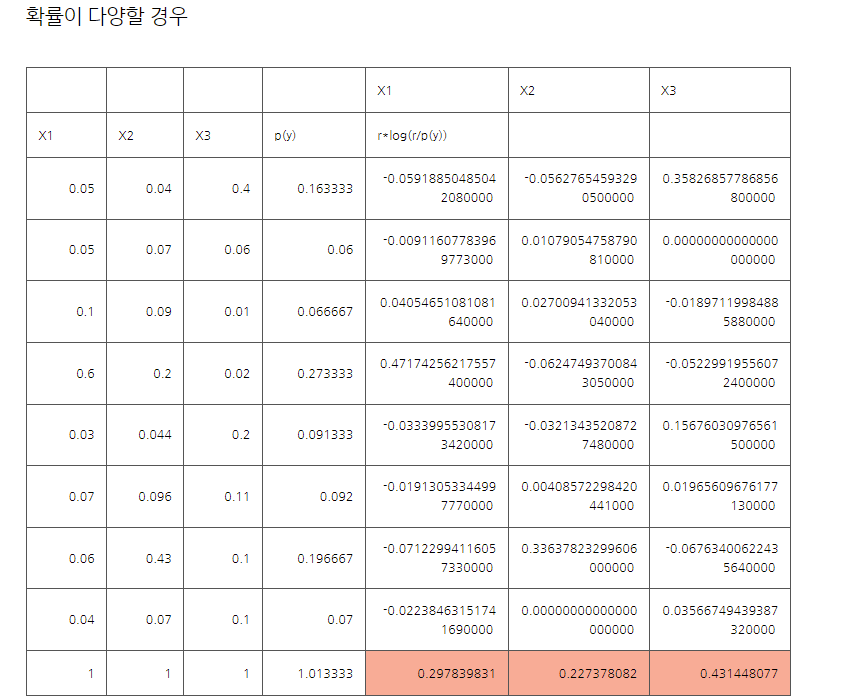
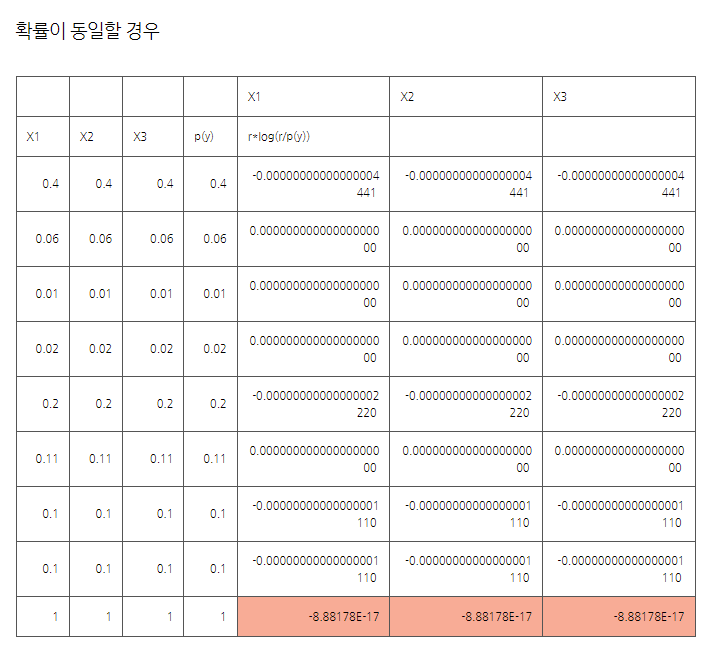
*음수값 발생 이유: marginal 합이 1이 넘는다.(sampling 오차)

단점

• pre trained된 특정 분류기를 사용하기 때문에 사용되지 않은 class의 이미지에 대해선 (ILSVRC 2014 dataset) 항상 낮은 IS값을 받을 수밖에 없다.(이미지가 특정 label로 분류되지 않는다.)

• Inception 분류기와 생성된 이미지의 label set가 다른 경우, 예를 들면 생성기가 애초에 다양한 개 이미지를 생성시키도록 학습되었다면 매우 다양한 개 이미지를 생성하더라도, Inception 분류기의 class가 다양한 label로 이루어져있기 때문에 다양성이 낮게 평가된다.

• 계속해서 클래스당 하나의 품질이 좋은 이미지만을 생성한다면, p(y)가 균등하게 계산되기 때문에 실질적인 다양성이 고려되지 않을 수 있다.

• 실제 데이터가 아닌 fake image만을 가지고 평가된다. (실제 이미지와 정말 비슷한가? 여부를 판단하기 어렵다. Inception의 평가에 의존하게 때문에 윤곽만 가지고 있을 수도..)

(2) FID(Frechet Inception Distance)

FID는 기존의 IS를 개선시키기 위해 (특별히 GAN 성능 평가에 대해서) 개발 되었다.

IS가 생성된 이미지만을 사용하는 반면, FID는 대상 도메인의 실제 이미지 모음의 통계 값과 생성된 이미지 모음의 통계 값을 비교해 평가를 진행한다.

먼저 생성된 이미지와 실제 이미지를 Inception v3의 FC layer를 제외한 네트워크에 통과시켜 임베딩을 만든다.(2048)

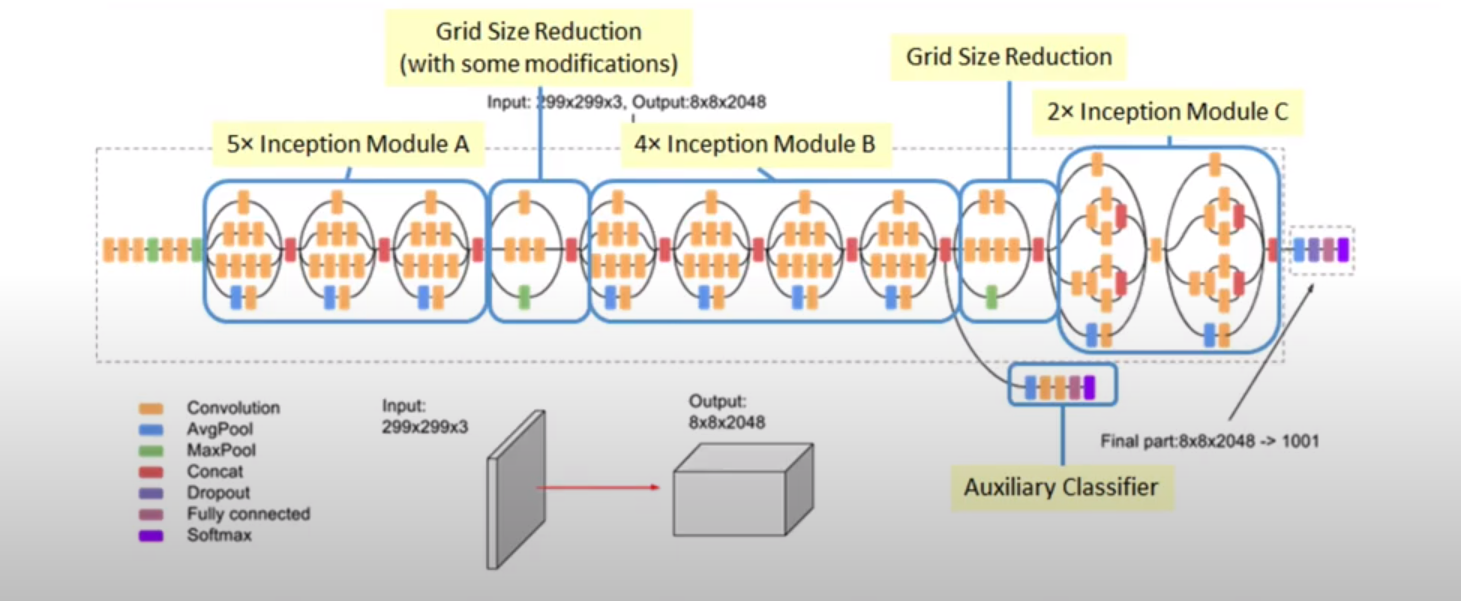
class PartialInceptionNetwork(nn.Module):

    def __init__(self, transform_input=True):
        super().__init__()
        self.inception_network = inception_v3(pretrained=True)
        self.inception_network.Mixed_7c.register_forward_hook(self.output_hook)
        self.transform_input = transform_input

    def output_hook(self, module, input, output):
        # N x 2048 x 8 x 8
        self.mixed_7c_output = output

    def forward(self, x):
        """
        Args:
            x: shape (N, 3, 299, 299) dtype: torch.float32 in range 0-1
        Returns:
            inception activations: torch.tensor, shape: (N, 2048), dtype: torch.float32
        """
        assert x.shape[1:] == (3, 299, 299), "Expected input shape to be: (N,3,299,299)" +\
                                             ", but got {}".format(x.shape)
        x = x * 2 -1 # Normalize to [-1, 1]

        # Trigger output hook
        self.inception_network(x)

        # Output: N x 2048 x 1 x 1 
        activations = self.mixed_7c_output
        activations = torch.nn.functional.adaptive_avg_pool2d(activations, (1,1))
        activations = activations.view(x.shape[0], 2048) #2048 x num_images로 변환
        return activations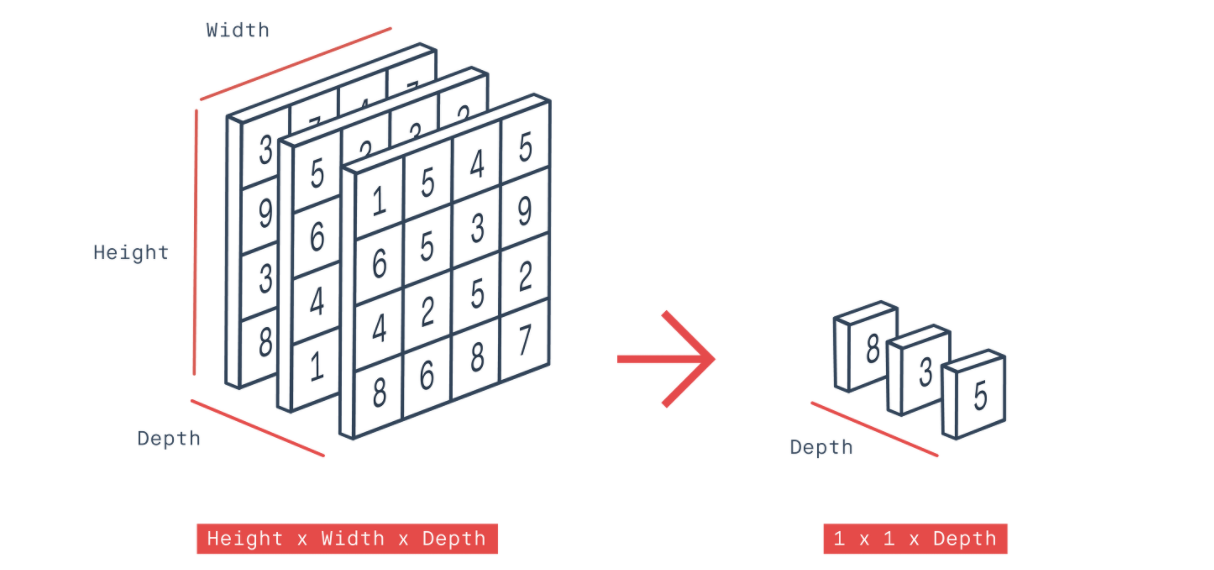

*Inception의 feature 추출 네트워크가 특징을 잘 추출 한다는 것을 전제로 한다.
->다른 신경망의 feature 추출 네트워크를 사용할 수도 있다.(vgg, custom...)

그 임베딩을 갖고 실제 이미지와 생성된 이미지의 평균과 공분산을 계산하여 다변량 가우시안으로 요약한 뒤, 이러한 두 분포사이의 거리를 Wasserstein-2 distance라고 불리는 Frechet distance를 사용해 측정한다.

fake 이미지와 real 이미지의 거리를 측정하기 때문에 낮을 수록 좋은 성능이다.

*가우시안 전제의 이유: 가우시안이 최대 엔트로피 모델

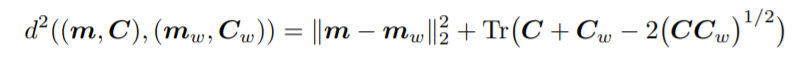
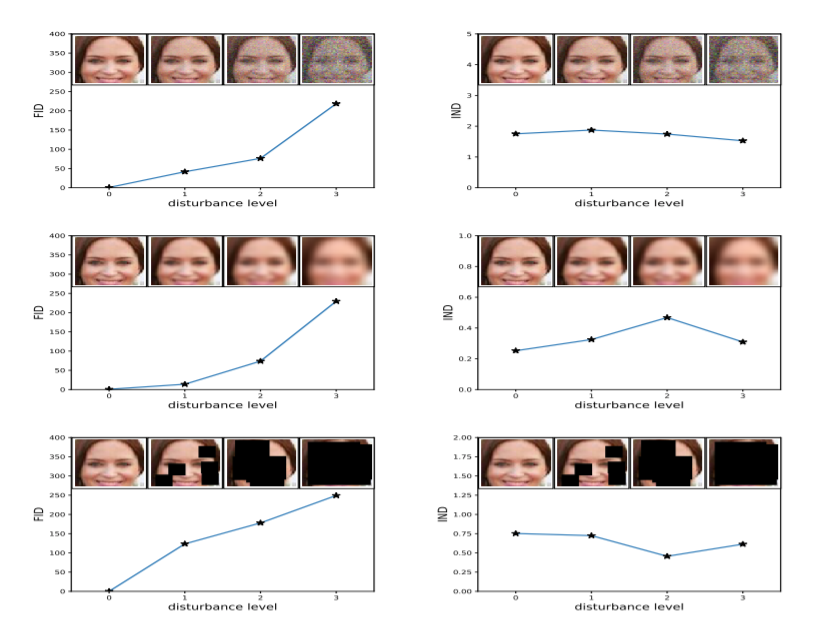
좌측 FID와 우측 IS를 비교했을 때 좌측 FID가 noise를 더 잘 잡아내는 것으로 나타났다.

생성하는 이미지 집합과 실제 이미지 집합간의 분포를 직접 비교하기 때문에, 클래스당 하나의 이미지만 생성하는 경우에도 거리 값이 높아진다.
(다양성을 측정하는 데 적절하다.)

*실제 데이터의 평균과 공분산은 매번 계산하지 않고 따로 저장해서 사용하는 경우가 많다.

단점

• 역시 Inception v3 모델을 이용하기 때문에 pre-trained 당시에 이용된 데이터와 다른 종류의 데이터를 다룰 경우 원하는 특징이 잘 추출되지 않을 수 있다.

• 이미지 임베딩의 분포를 가우시안으로 전제했기 때문에, 제한적인 통계량(평균, 분산)만으로 분포의 차이를 잘 설명하지 못할 수도 있다.

---

GAN 평가1

GAN 평가2

GAN 평가3

GAN 평가4