작성자 : 김재희

0. Intro

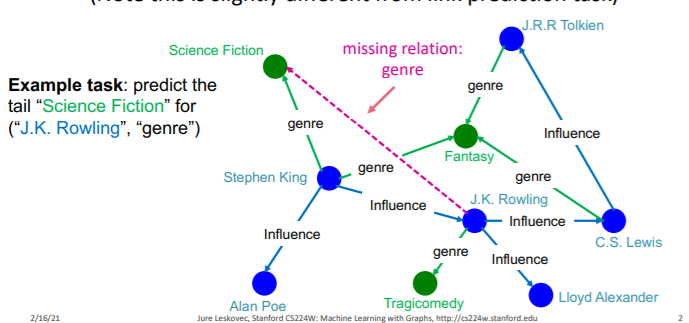
이번엔 지난 시간에 다룬 지식 그래프를 이용해 새로운 지식을 얻어내는 방법을 알아보도록 하자. 이전에 배운 KG completion task는 head와 relation이 주어졌을 때, 현재 그래프에 연결되어 있지만, 연결될 가능성이 높은 tail을 예측하는 태스크였다. 즉, 위와 같이 J.K. Rowling이라는 작가와 genre가 주어졌을 때, S.F.가 연결되어 있지만, 연결될 가능성이 높다는 것을 알아내는 작업이다. 이를 조금 확장해보면 우리는 지식 그래프가 온전하지 못한 상태에서 개념이나 관계의 결합을 통해 필요한 지식을 얻어낼 수 있지 않을까? 즉, KG completion이 1 hop에 해당하는 지식을 얻어내는 작업이라면, 이를 n hop으로 확장할 수 있지 않을까?

이와 같이 지식 그래프를 이용해서 multi hop의 지식을 얻어내는 작업을 reasoning이라 한다.

1. Reasoning

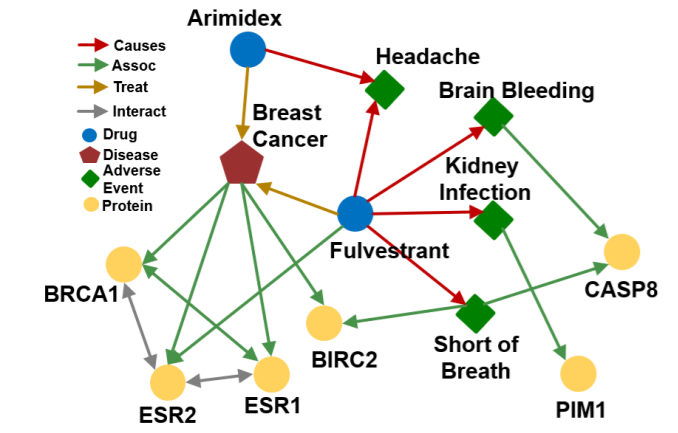
앞으로 위의 그래프를 예시로 reasoning을 살펴보도록 하자. reasoning도 쓰기 귀찮으니 앞으론 추론이라고 이야기하겠다. multi-hop 추론은 다음과 같이 간단하게 3가지 방법이 있다고 한다.

1-1. One hop Queries

위의 예시처럼 head와 relation이 주어진 상태에서 tail을 예측하는 작업이다. KG completion과 동일한 작업을 의미한다. 이는 현재 노드에서 정해진 엣지를 이용할 때, 어떤 노드로 이동할 지 정하는 작업이 될 거시다.

1-2. Path Queries

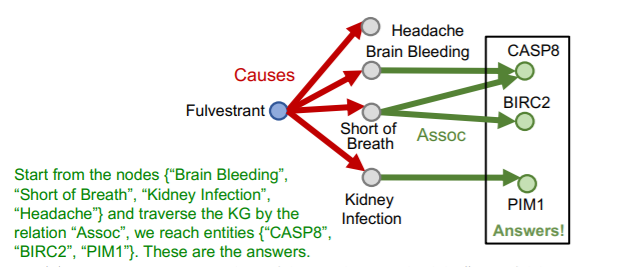
위의 예시처럼 Fulvestrant라는 노드에서 출발하여 n 개의 관계를 지나서 도달할 수 있는 노드를 추론하는 작업이다. 이때 출발하는 노드는 anchor라 하여 $v_a$로 표기한다. 전체 쿼리 $q$에 대해서는 다음과 같이 표기한다.

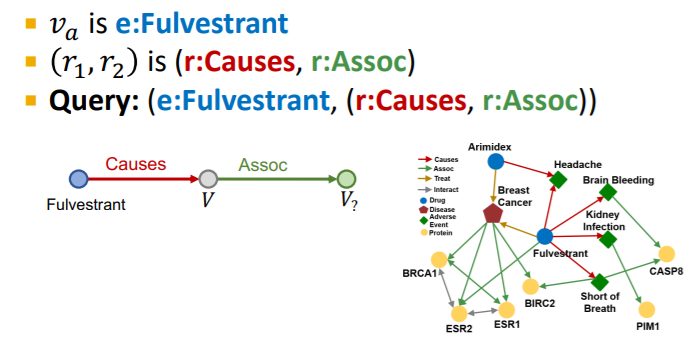
예를들어 Fulvestrant라는 노드가 anchor 노드로서 여기서 출발할때, causes relation을 지나 어떤 노드 $V$에 도달하고, 해당 노드에서 다시 Assoc relation을 지나 도달하게 될 노드가 무엇일지 찾는 태스크이다. 이를 위의 노테이션으로 표기하면 다음과 같을 것이다.

그 과정을 뜯어보면 다음과 같다.

1. 우선 시작 노드에서 출발해서 해당 relation(causes)으로 연결된 모든 노드로 뻗어나간다.
   

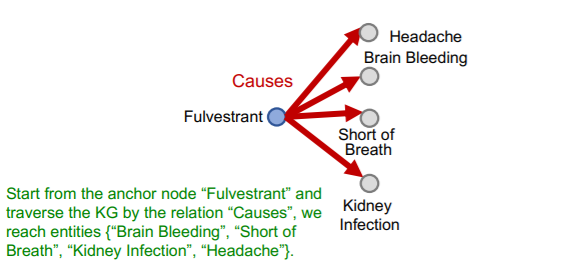
2. 1에서 뻗어나간 노드에서 다시 두번째 relation(assoc)으로 연결된 모든 노드로 뻗어나간다. 이때 뻗어나간 노드들이 우리가 구하고자 한 값이다.
   

1-3. Conjunctive Queries

conjunctive queries는 다수의 (head, relation) 쌍이 주어진 상태에서 공통된 tail을 찾는 태스크이다. 예를 들어 폐암(head)을 치료(relation)하면서, 편두통(head)를 유발(relation)하는 노드(tail)은 무엇일지 찾는 작업등을 의미한다.

2. Path Queries

우선 path queries에 대해 자세히 생각해보면, 언뜻 보기에는 주어진 그래프에서 그저 엣지를 따라가면 해답을 얻을 수 있을 것 같다.

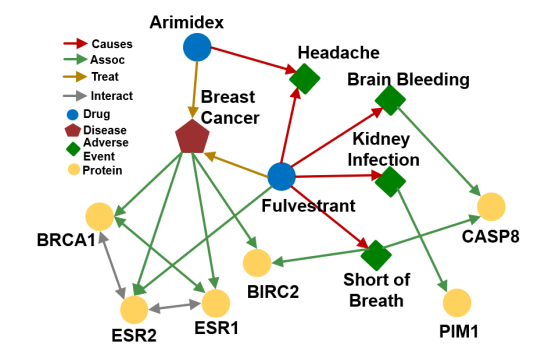
즉, 위와 같이 주어진 그래프에서 fulvestrant 에서 시작하여 cause 엣지를 따라가고, 거기서 다시 assoc 엣지를 따라가면 (e: fulvestrant, (r:cause, r: assoc))을 만족하는 path queries 태스크를 수행할 수 있을 것 같다. 위 그래프에 따르면 이는 PIM1과 CASP8이 된다.

하지만 이전 시간에 배웠듯이 지식 그래프는 매우매우매우매우 많은 엣지가 비어있는 상태이다. 이는 페이스북에서 사람들이 자신의 프로필을 모두 채우지 않아서일 수도 있고, 제약 분야에서 아직 인류가 발견하지 못한 단백질과 질병의 관계 때문일 수도 있으며, 사람들이 아직 위키피디아를 업데이트 하지 않아서 테슬라에서 신차를 출시했다는 사실이 업데이트 되지 않아서일 수도 있다.

무슨 이유에서든 지식 그래프는 매우 불완전한 연결을 띄고 있고, 이 상황에서 주어진 그래프에서 탐색 알고리즘을 이용해 위 세가지 태스크를 수행하는 무의미하다. 방금 말한 예시에서도 아래 그림처럼 Fulvestrant와 Short of Breath에 대한 연결이 없어, BIRC2로 연결되지 못하지만, 실제로는 관련이 있을 수 있다.

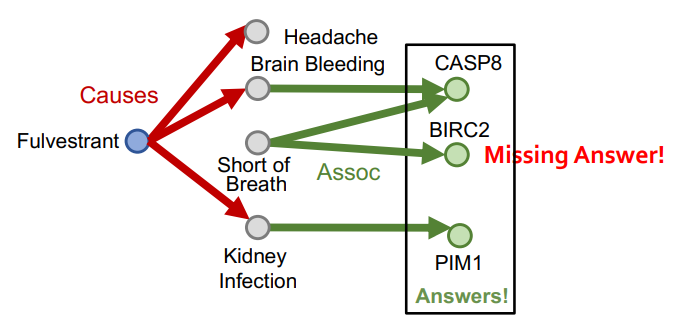
이 지점에서 가장 먼저 할 수 있는 생각은 저번 수업에서 배운 KG completion을 이용해서 그래프를 완성시키고, 완성된 그래프에서 탐색 알고리즘을 수행하면 되지 않을까?일 것이다. 하지만 그래프를 완성한다는 것은 거의 불가능에 가까운 작업니다.

거의 모든 (head, relation, tail) 쌍이 어찌되었 간에 연결될 가능성이 0이 아니기 때문에, 모든 가능한 연결을 잇고, 이를 탐색하기 위해서는 $O(d^L)$의 시간 복잡도를 가지는 일이 된다. 페이스북이나 구글이 가진 지식 그래프의 크기가 정말 말도 안되게 크다는 것을 생각하면, 이는 가능한 선택지가 아닐 것이다.

2-1. Predictive Queries

그래서 수행하는 것이 predictive queries이다. 이는 실제로 그래프를 완성하지 않은 상태에서, 주어진 query에 대해 (head, relation)에 대응하는 tail을 찾는 작업을 의미한다. 즉, 태스크 도중 이어지지 않은 relation 중 가능한 relation은 이어져있다고 보고, 가장 최적의 tail을 찾게 된다. 이는 link prediction task을 확장한 것이라고 볼 수 있는데, 주어진 head와 relation에 대응되는 tail을 찾는 link prediction처럼, 주어진 head와 다수의 relation에 대응되는 tail을 찾는 작업이 되기 때문이다.

이에 대한 구체적인 방법은 이전 시간에 배운 KG embedding을 활용하는 것이다. 여러 KG embedding 중에서도 TransE를 활용할 수 있다. 이전 시간에 배웠듯이 TransE는 노드와 엣지를 모두 동일한 벡터 공간에 임베딩한다. 이를 통해 KG completion을 head + realtion = tail 이 되도록 각 임베딩 벡터를 구성한다.

예를 들어 버락 오바마라는 노드와, 국적이라는 엣지가 있다면, 두 임베딩 벡터의 합이 미국이라는 노드 벡터와 동일하도록 만드는 것이다.

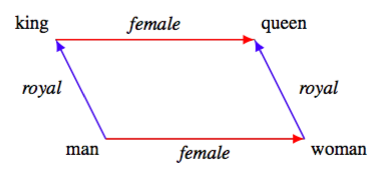
저번 시간에 배웠듯이, TransE는 이러한 특성으로 인해 relation을 합성할 수 있다. 예를 들어, King(entity) - Man(relation1) + Woman(relation2) = Queen으로 만들 수 있는 것이다. 즉, 주어진 head에 대해 여러 relation을 거친 tail이 무엇인지 알 수 있다! 우리가 path query에서 하고자 하는 일이 바로 이것이다!

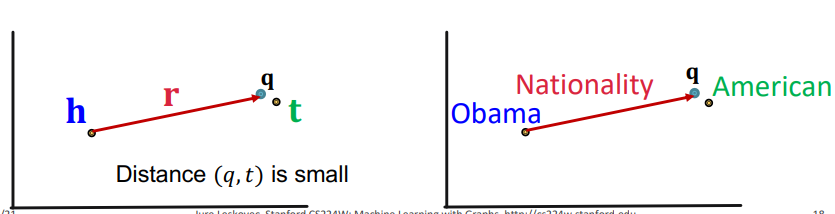
실제로 path query에서 수행하는 것은 아래와 같다.

주어진 $q = (v_a, (r_1, \dots, r_n))$에 대해 모든 벡터를 합하여 $q$ 벡터를 만든다. 그리고 $q$ 벡터와 가장 가까운 entity 벡터를 찾아 tail로 예측하게 된다. 이를 통해 이전에는 복잡한 그래프 구조에서 모든 경우의 수를 따져가면서 탐색 알고리즘을 돌려야 했던 문제에서, 단순히 선형 연산을 하면 되는 문제로 바뀌게 되었다. 이는 아무리 그래프가 크고, 노드가 많고, 엣지가 많더라도 연산량이 늘어나지 않는다는 것을 의미한다.

구체적인 예시를 통해 하나씩 살펴보자.

• 질문 : 어떤 단백질이 Fulvestrant(head)에 의해 유발(relation1)되는 부작용(entity)과 연관(relation2)되는 단백질(tail)이야?
• $q = (e : \text{Fulvestrant}, (r:\text{Causes}, r: \text{Assoc}))$

1. head 임베딩 벡터에서 시작하자.
   
2. 첫번째 relation의 임베딩 벡터와 head 임베딩 벡터를 더한다.
   
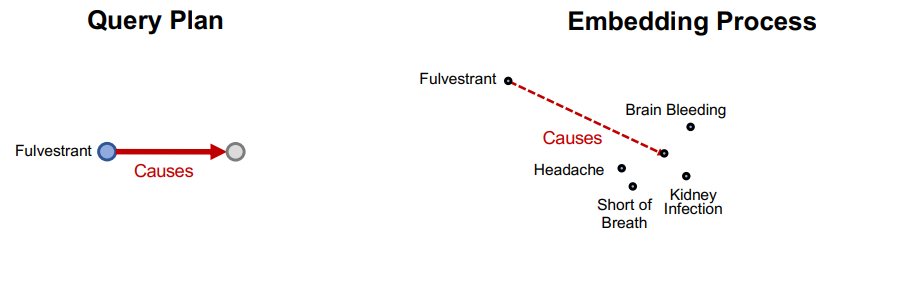
3. 두번째 relation의 임베딩 벡터와 2의 벡터를 더한다.
   
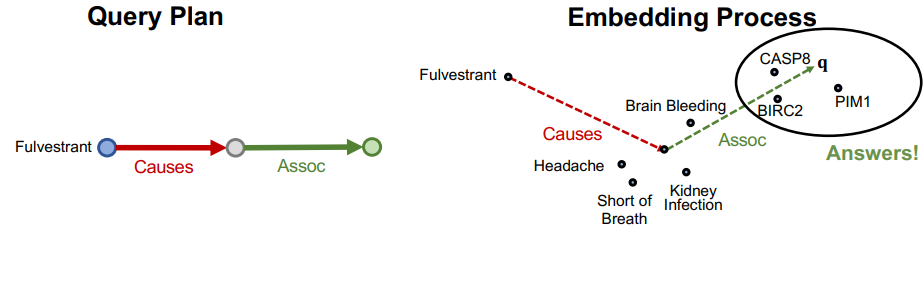
4. 3의 벡터와 가장 가까운 entity 임베딩 벡터를 찾아 예측값으로 한다.

유의할 점은 TransE가 entity와 relation을 동일한 벡터 공간에 맵핑하여 composition 관계, 관계를 합성할 수 있지만, 이외의 TransR, DistMult, ComplEx 등의 지식 그래프 임베딩 방법론은 그렇지 않기 때문에, composition 관계를 다루지 못한다는 점이다. 이로인해 path query 문제를 위와 같이 풀 수가 없게 된다.

3. Conjunctive Queries

Conjunctive Queries는 하나의 anchor entity를 가지지 않는다. 위의 그림에서 보이듯이 다수의 anchor entity가 각자의 path query를 가지고, 그 path query의 합성으로 올 수 있는 tail을 예측하는 태스크이다.

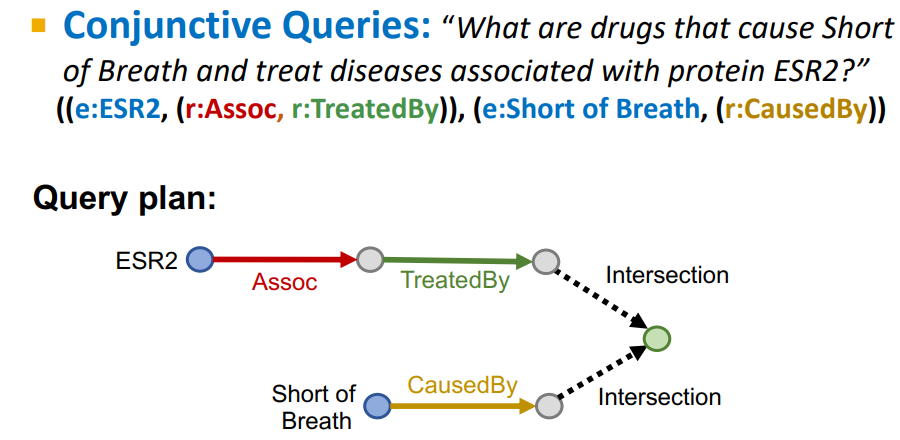
예를 들어 위와 같은 문제가 있다고 하면, 우리는 ESR2(anchor entity)에서 시작하여 Assoc(relation1)인 entity에서 TreatedBy(relation2)이면서, Short of Breath(anchor entity)에서 시작하여 CasedBy(relation3)인 tail을 찾는 태스크인 것이다.

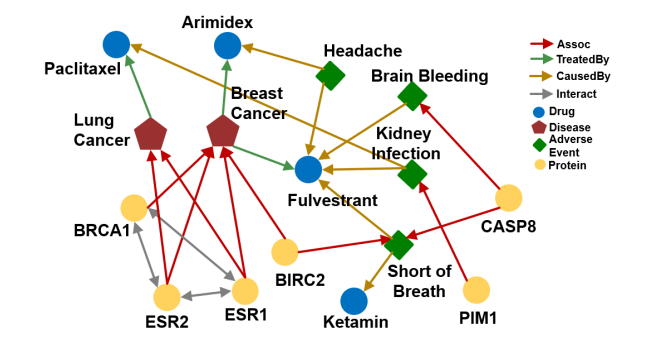
우선 이를 모든 엣지가 구현된 위와 같은 지식 그래프에서 수행한다고 생각해보자.

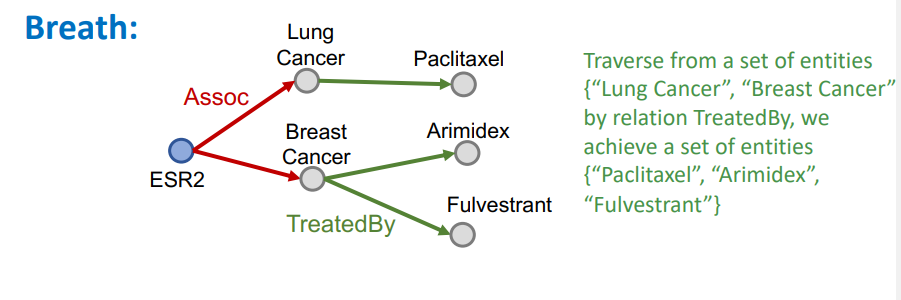
ESR2에서 시작하는 탐색 방향에선 Assoc에 해당하는 entity 집합을 찾고, 해당 집합에 대해 TreatedBy로 연결된 entity 집합을 찾아가게 된다.

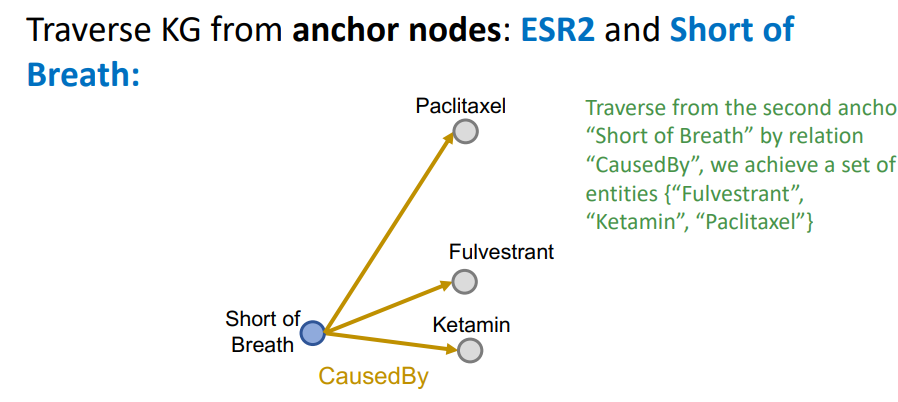
이는 Short of Breath에서 시작하는 탐색 방향에서도 마찬가지일 것이다.

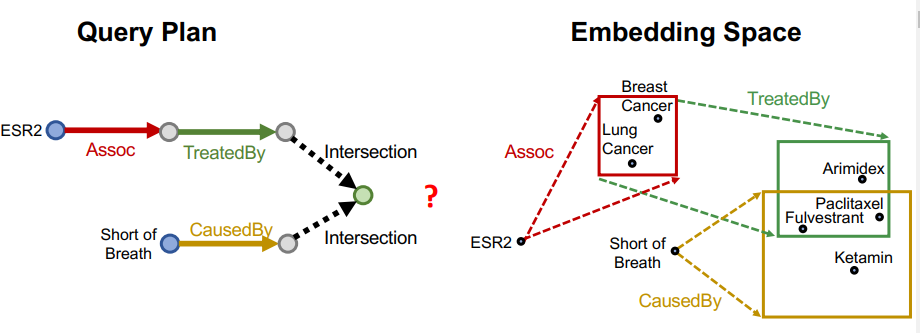
이렇게 두 탐색 방향에서 찾은 tail 후보 집합이 존재할 때, 우리는 두 집합의 교집합으로 tail을 찾게된다. 즉,

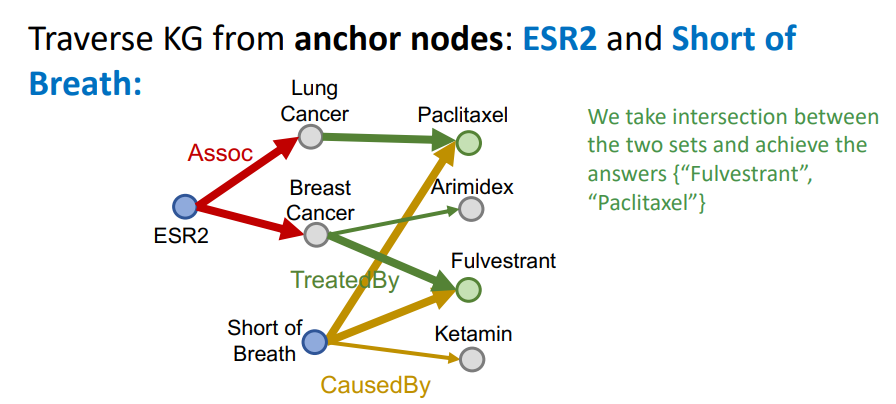
위 그림과 같이 두 탐색 방향에 모두 해당하는 Paclitaxel이나 Fulvestrant를 tail로 선택하게 될 것이다.

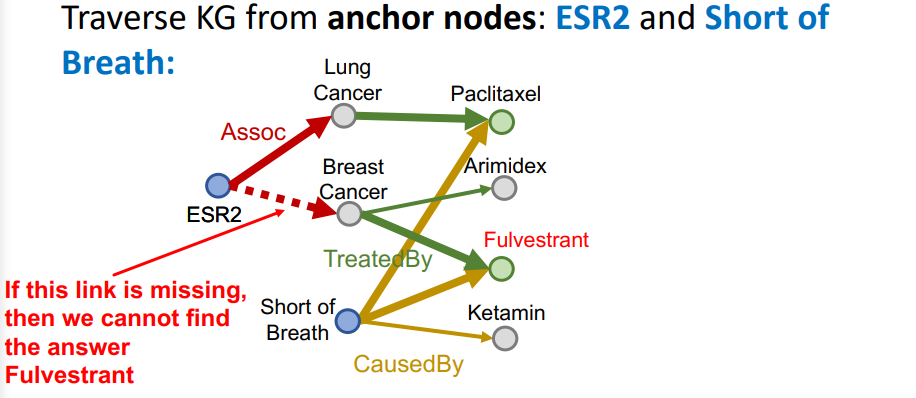
하지만 당연하게도 우리가 다루는 그래프는 완전하지 않고, 비어있는 엣지가 존재하게 된다. 위 그림과 같이 ESR2와 Assoc 엣지가 하나 빠지게 되면, Fulvestrant는 tail로 선택할 수 없게 된다.

Path Query에서 했던 것처럼 이번에도 역시 임베딩 공간을 이용해서 이와 같이 비어있는 엣지에 대한 문제를 해결해야 할텐데, 이전과 다른 문제가 있다.

• Path Query : 모든 엣지에 대한 임베딩 벡터가 존재하여, 단순히 더하기만 하면 됨.
• Conjunctive Query : 두 anchor node에서 시작하기 때문에, 단순히 더해서 해결되지 않음.

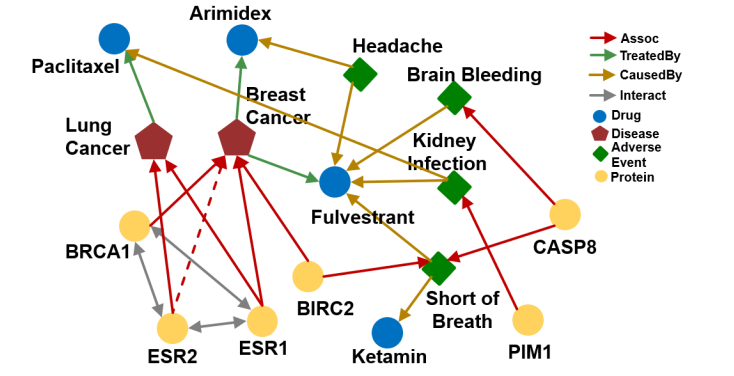
위 그림처럼 ESR2와 Breast Cancer이 연결되어 있지 않은 상황에서, 우리는 ESR2와 연결되어 있는 BRCA1이나 ESR1이 Breast Cancer과 연결되어 있기 때문에, 자연스레 ESR2가 Breast Cancer과 연결될 것이라는 판단을 할 수 있다. 이를 모델이 잠재적으로 할 수 있도록 만들어야 한다.

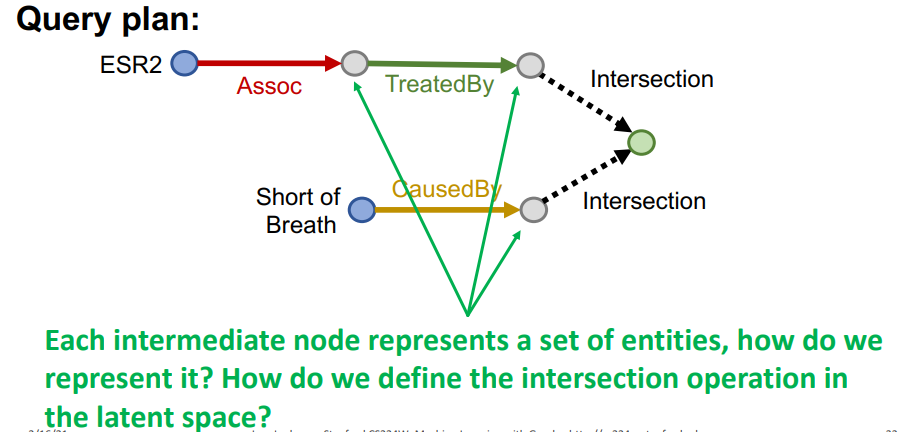
이때, 위 그림처럼 각각의 query path가 하나의 노드처럼 표현되어 있지만, 사실은 노드 집합이라는 점을 명심해야 한다. 즉, ESR2와 Assoc으로 연결된 노드는 하나가 아니라 다수의 노드이므로, 노드 하나처럼 표현되어도 사실 노드 집합이라는 이야기다. 이를 정리해보자면 다음과 같을 것이다.

• anchor node 1 -> (relation1) -> set of entity1 -> (relation2) -> set of entity2
• anchor node 2 -> (relation3) -> set of entity3
• f(set of entity2, set of entity3) = 최종 결과

여기서 함수 f는 두 집합의 교집합을 찾는 등의 상호작용 연산을 담당하는 부분이 된다.

위 과정을 임베딩 공간에서 진행해야 하는데 , 그것이 바로 Query2Bow이다.

4. Query2Box

4-1. 임베딩 벡터

우선 query2box에서도 노드들은 임베딩 공간에 맵핑된다. 그리고, query(entity + relation)은 박스의 형태로 임베딩 공간에 표현된다. 예를 들어 Fulvestrant(anchor node)의 adverse event(relation)이 1)Short of Breath 2)Kidney Infection 3) Headache(tails) 일때, 다음과 같이 query를 표현할 수 있다.

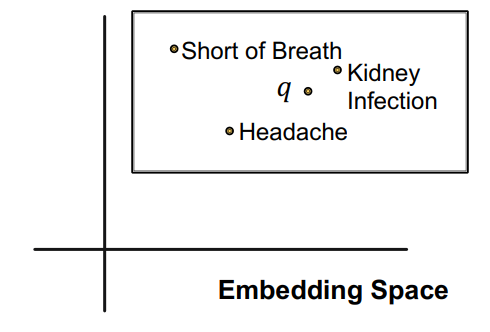
즉, 해당 query의 tail들은 query를 박스로 표현한 직사각형 내부에 위치하게 된다. 이때 박스는 박스의 중심점 $center(q)$와 크기 $offset(q)$로 표현한다. 이렇게 query를 표현할 경우 얻을 수 있는 이점은 다음과 같다.

1. 직전에 이야기한 두 집합의 상호작용 연산이 매우 단순해진다. 두 query가 겹치는 부분으로 선택하면 되기 때문이다.
2. 박스의 중심과 크기만으로 query가 표현가능해진다.

여기서 구체적으로 요소들을 짚어보자.

• Entity embedding($d|V|$) : query2box에선 entity embedding 벡터도 실제로는 크기가 0인 박스로 취급한다. 점과 다르게 박스는 면적이 있으므로 늘리거나 줄일 수 있기 때문이다.
• Relation embedding($2d|R|$) : 아래에서 projection operator를 다루면서 왜 파라미터 수가 이러한지 살펴보자.
• Intersection operator f(learnable parameters)

4-2. Projection Operator

우선, projection operator g가 등장한다. 이는 relation embedding에 따라 주어진 박스를 이동시키고, 크기를 줄이거나 늘리는 역할을 하는 연산자이다. 즉, 현재의 박스와 relation을 입력으로 받아 이동된 박스를 내뱉는다.

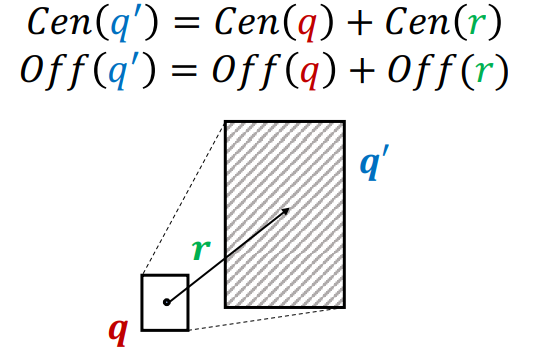
연산은 무척 단순하다. 그냥 기존의 박스 $q$에 relation 벡터를 선형결합하는 모습을 띄고 있다. 이때, 변화된 $Cen(q')$은 박스의 중심을 이동시키게 되고, $Off(q')$은 박스의 크기를 늘리거나 줄여, 해당 relation의 tail에 해당하는 노드 집합이 박스 안에 모두 들어오도록 한다.

4-3. 연산과정

이제 계속 보고 있는 예시를 통해 단계별로 query를 박스로 표현하는 과정을 살펴보자.
1. anchor node 임베딩 벡터 표현.
anchor node의 임베딩 벡터는 오른쪽에서 볼 수 있듯이 크기가 0인 박스로 표현된다. 이때 박스이기 때문에 projection operator를 통해 크기가 늘어나거나 줄어들수도 있고, 위치가 변화할 수도 있다.

2. $q = g(\text{ESR2}, \text{Assoc})$에 대한 projection operator 수행
   기존의 anchor 노드에서 Assoc이라는 relation 임베딩 벡터에 해당하는 projection operator를 수행하게 된다. 그 결과 오른쪽 그림과 같이 tail에 해당하는 노드 집합이 모두 안에 들어가는 사각형으로 위치와 크기가 변화하게 된다.
   

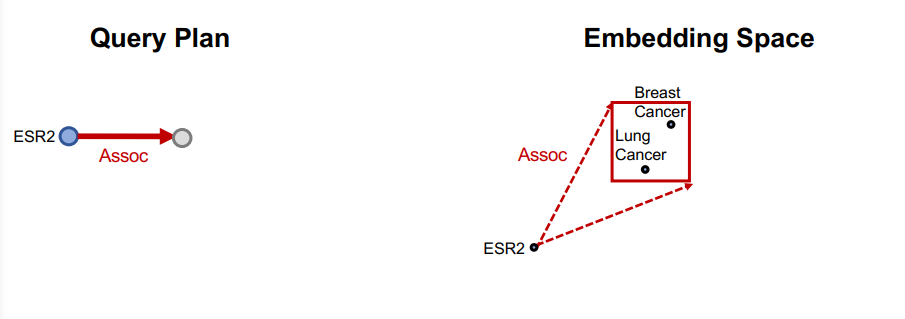
3. $q' = g(q, \text{TreatedBy})$에 대한 projection operator 수행
   이제 다시 새로운 relation이 주어졌기 때문에, 그에 맞는 tail이 박스 안에 모두 들어오도록 기존의 박스에서 새로운 박스로 중심과 크기가 변화하게 된다.
   

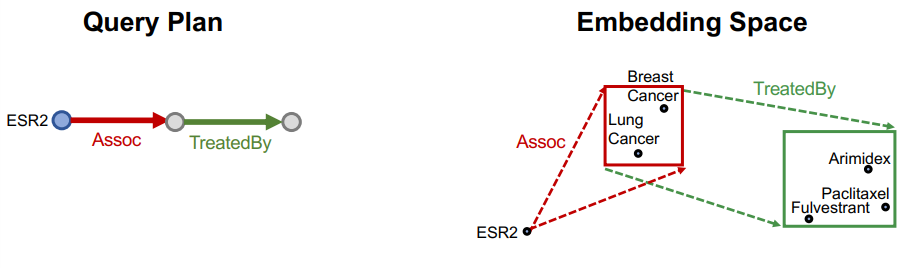
4. $q = g(\text{Short of Breath}, \text{Caused By})$에 대한 projection operator 수행
   다른 anchor 노드에서 출발한 노드 집합을 구하기 위해 새로운 박스가 생겨나게 된다.
   

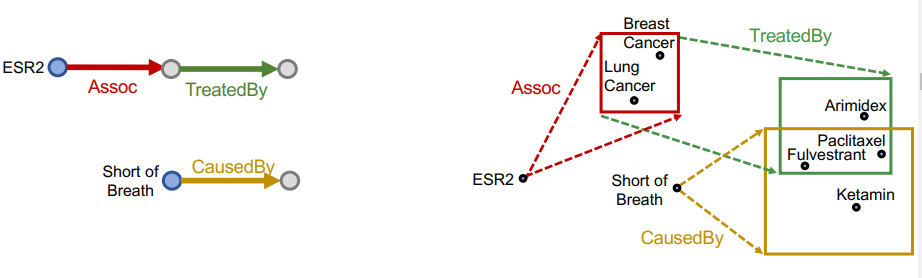
5. 두 노드 집합 간 상호작용 연산
   최종적으로 구해진 두 노드 집합에 대해 상호작용을 연산해야 한다. 즉, 왼쪽 그림처럼 두 후보 노드들 간에 어떤 노드가 교집합이 생기는지 알아야 한다.
   

4-4. Intersection Operator

두 노드 집합 간 상호작용 연산을 직관적으로 두 박스의 겹치는 부분으로 정하면 좋겠지만, 실제로는 또다른 연산자를 이용해 구하게 된다고 한다. 이때 박스의 겹치는 부분으로 정하는 방식을 통해서 이 연산자가 가져야 할 성질들을 알 수 있다.

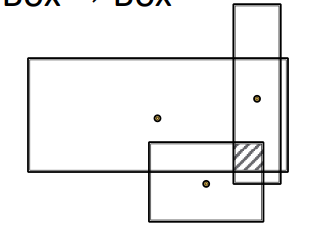
위와 같이 연산자에 세 박스가 들어가게 되면 세 박스의 겹치는 부분인 빗금친 부분이 상호작용된 박스라고 하자. 이 박스의 특징은 다음과 같을 것이다.

1. 새로운 박스의 중심은 입력값으로 사용된 박스의 중심들과 가까워야 한다.
2. 새로운 박스의 크기는 줄어들어야 한다. 즉, 입력값으로 사용된 박스 중 가장 작은 박스보다 작아야 한다.

두가지 특징을 intersection operator가 어떻게 구현하고 있는지 하나씩 살펴보자.

Center
중심은 다음과 같이 계산된다.

이를 잘 살펴보면,

1. 각 박스의 중심 벡터가 임의의 함수 $f_{cen}$을 통과하고, 소프트맥스 함수를 통과하여 가중치 벡터 $w_i$가 된다.
2. 가중치 벡터 $w_i$와 실제 중심을 나타내는 벡터를 아다마르 곱하여 가중합한다.

의 과정으로 이루어져있는 것을 알 수 있다. 이 전체 과정은 결국 트랜스포머 등에서 쓰이는 self attention 구조를 띄고 있는 것을 알 수 있는데, 이때 $f_{cen}$는 나중에 다루도록 하고, 전반적인 의미만 보자. 전반적으로 결국 입력값으로 주어진 박스 중심들에 대해 가중합하여 중심들과 근접한 점을 새로운 박스의 중심으로 삼고 있는 것을 알 수 있다.

Offset
크기는 다음과 같이 계산된다.

크기는 가장작은 박스의 크기보다 줄어야 하기 때문에, 시그모이드 함수를 이용하고 있다. 아다마르 곱을 중심으로 앞의 항은 입력 박스 중 가장 작은 박스를 고르는 과정이고, 뒤의 항은 입력 박스들의 크기 벡터를 입력으로 하는 어떠한 함수 $f_{off}$를 통과한 벡터에 대해 시그모이드 함수를 취해주고 있다. 이때 $f_{off}$ 역시 뒤에서 나오겠지만, 박스들의 크기에 대한 representatioin을 생성해주는 역할을 한다. 결국 새로운 박스의 크기는 가장작은 박스의 크기보다 element wise하게 축소시켜주게 된다.

이때 $f_{cen}$과 $f_{off}$ 모두 임의의 NN을 이용한 함수로 단순하게 겹치는 부분에 대해 추출하기보다 더 효과적으로 representation을 구하여 모델의 표현력을 높여주기 위해서 도입되었다고 한다.

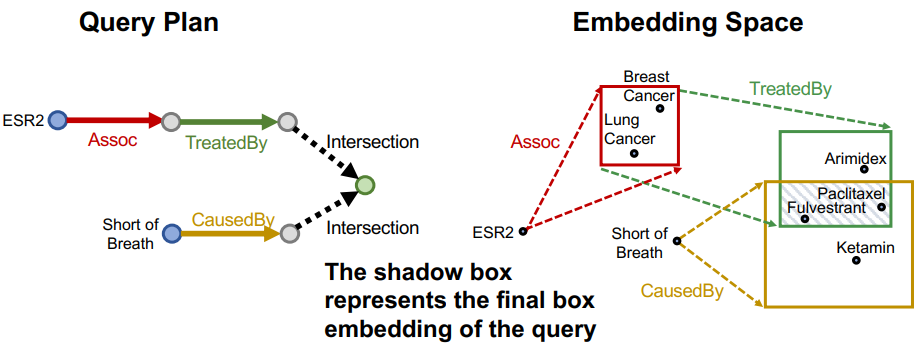
최종적으로 intersection operator에 의해 위와 같은 결과가 주어지게 될 것이다. 지금까지 tail 노드에 해당하는 노드 집합은 박스 안에 있어야 한다고 언급했다. 즉, SVM에서 초평면을 결정경계로 삼아 분류 태스크를 수행하듯이, Query2Box도 박스의 경계선을 경계면으로 삼아 일종의 분류 태스크를 수행하고 있다고 볼 수 있을 것이다(주의 : 뇌피셜임 강의 내용 아닙니다.).

4-5. Entity-to-Box Distance

그런데 SVM에서 생각해보면, hard SVM, 즉, 초평면에 대한 예외를 허용하지 않으면, 오차가 커지게 되고 모델이 outlier에 상당히 큰 영향을 받게 된다. 모델의 강건함이 떨어지게 되는데, 이는 데이터가 이상적으로 깔끔하지 않고, 노이즈가 껴 있기 때문일 것이다. 이처럼 Query2Box에서도 박스 내부의 노드만 결과 노드로 사용하지 않고, 박스와 가까운 노드에 대해서도 결과 노드로 사용하고 있다.

그렇다면 박스는 직사각형의 형태라, 단순히 유클리디언 거리를 사용하지 못하는데, 어떻게 박스로부터 각 노드까지의 거리를 구해서 결과노드를 산출할까?

이는 박스의 중심으로부터 거리를 구해서 사용하게 된다. 우리는 이상적인 결과 노드는 최종적인 박스의 중심에 가까워야할 것이라는 직관은 있다. 그래서 박스 중심으로 부터 거리를 재면 될 것이다. 하지만 이때, 어찌되었건 박스 안에 있다면, 어느 정도는 옳바르게 선택된 노드이므로, 거리에 대한 가중치를 줄이고, 박스 밖에 있을 경우에만 본래 거리를 사용하면 된다. 최종적으로 식은 다음과 같다.

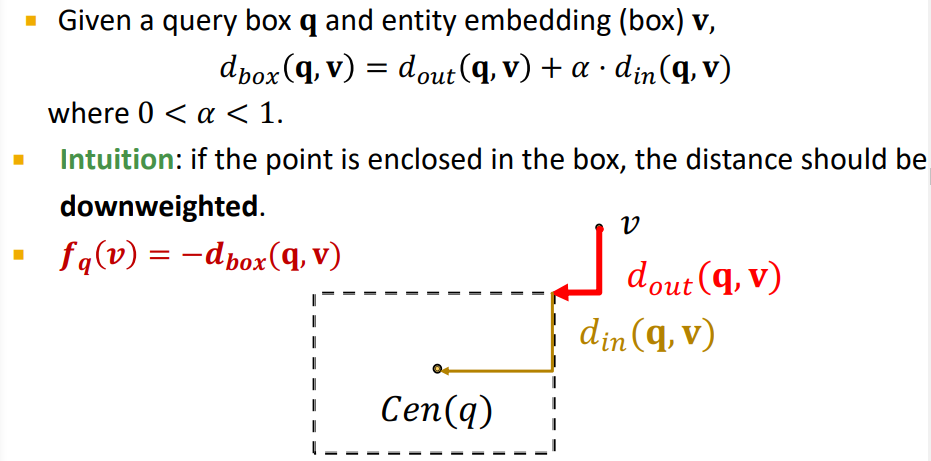
즉 거리를 산출하는 함수 $f_q(v)$는 노드 $v$에 대해 박스 경계면까지의 거리는 그대로 사용하고, 박스 경계면 내부의 거리는 가중치를 주어 좀 더 작게 측정하게 된다. 이를 통해 박스 내부의 점은 거리가 실제보다 작게 측정되는 반면, 박스 외부의 점은 박스 경계면까지 그대로 거리가 측정될 수 있다.

4-6. And-OR Query

지금까지 다룬 상호작용은 두 노드 집합간의 and 연산이었다. 즉, a 노드 집합에도 속하면서 b 노드 집합에도 속하는 노드 집합을 구하고자 했다. 반대로, or 연산도 지금처럼 작은 차원의 임베딩 공간에서 가능할까? 결론부터 말하면 일단은 불가능하다. 예시를 통해서 직관적으로 이해해보자.

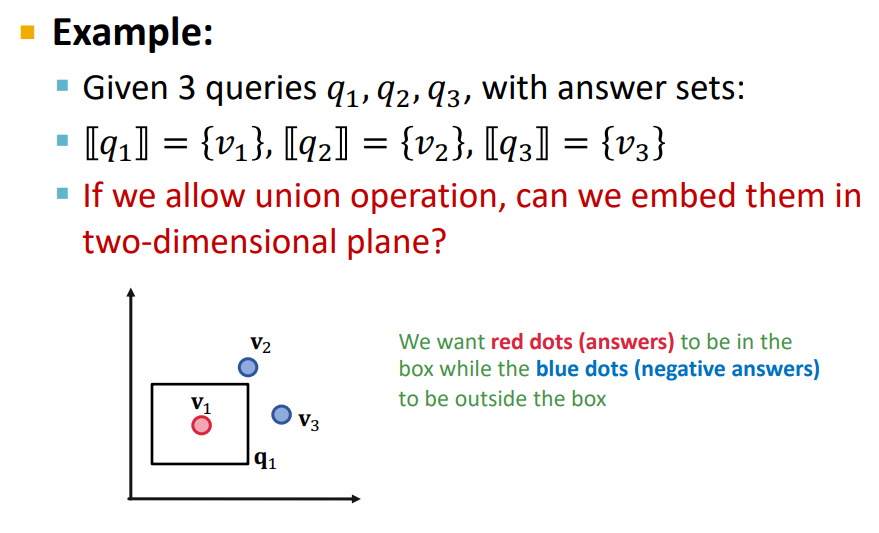
위 사진처럼 세 개의 query가 있고, 각 query마다 하나씩 정답 노드가 속해있다고 해보자. 그러면 아래 그림처럼 각 노드마다 하나씩 박스가 쳐져있는 형태가 될 것이다. 이때 query가 3개일때까지는 문제없이 or 연산이 가능하다.

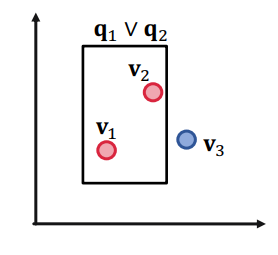
이렇게 쳐지는 박스를 구하면 될 것이기 때문이다.

하지만 query가 4개가 되는 순간 이야기가 달라진다.

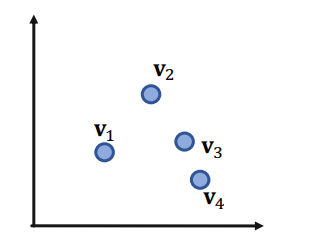
위와 같은 상황에서 각 노드마다 query box가 쳐져있다고 생각해보자.

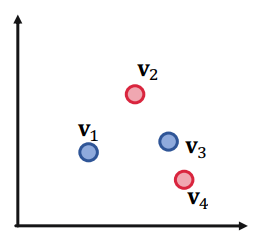
그런데 위처럼 $v_2$와 $v_4$에 대한 or 연산을 수행하려면,,,,? $v_3$노드는 포함되지 않는데 $v_2$와 $v_4$를 포함하는 기적의 직사각형을 구해야한다. 2차원에서는 절대 불가능한 연산이다.

이처럼 or 연산을 m개의 query에 대해 수행하려면, 최소한 m+1 차원의 공간이어야 한다고 한다. 그런데, 그래프는 노드가 많다... 비교적 작다고 알려진 FB15k도 노드 수만 14951개라고 하는데, 여기서 or 연산을 수행하려면 약 15000차원의 임베딩 벡터를 만들어야 한다. 이건 임베딩이 아니다...

하지만 해결책은 있다. and와 or이 함께 있는 and-or query의 경우 아래처럼 두 연산의 순서를 바꿀 수 있다.

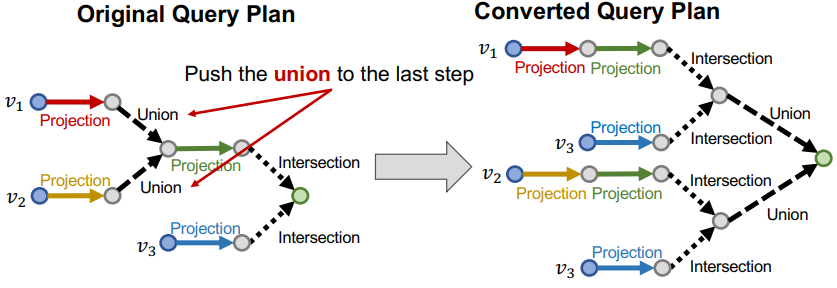
식으로 써보자면 $(a \cup b) \cap c = (a \cap c) \cup (a \cap b)$처럼 이야기할 수 있다. 즉, 우리는 $a \cup b$를 할 수 없지만, $a \cap c$와 $a\cap b$는 할 수있으므로, 두 query에 대해 or 연산을 제일 뒤로 미뤄놓자는 것이다. 모든 or 연산을 맨 마지막으로 미루는 것이 핵심이다. 이때 전체 query 크기가 커지기 때문에 연산량이 많아질 우려가 있지만, 실제로는 query 연산 자체가 워낙 간단해서 빠르기 때문에 큰 문제가 되지 않는다고 한다.

이렇게 마지막으로 미뤄놓은 or 연산은 실제로 수행하지 않는다. 우리는 결국 최종적으로 구한 박스와 실제 정답 노드 간의 거리를 구해서 그 거리를 최소화하는 목적함수를 세우게 될 것이므로, 실제로는 다음 연산을 하면 된다.

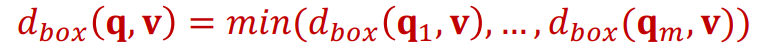
즉, and 연산을 모두 수행하여 or 연산만 남은 상태에서 어차피 or 연산의 각각의 항에 대해 정답 노드와 가장 거리가 짧은 박스와의 거리가 최종 박스와의 거리가 될 것이므로, 각 항의 박스와의 거리가 최소인 값을 최종 거리로 선택하게 된다(여기 글로 풀기 어려워서 모르시면 바로 이야기해주시면 정정해보도록 하겠습니다).

지금까지 이야기한 query2box의 전체적인 과정은 다음과 같다.

1. and 연산을 모두 수행하여 or 연산으로만 이루어진 query들을 만들어 낸다.
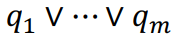
2. 각 query의 임베딩을 구한다(박스를 구한다)
3. 각 query와 노드 $v$와의 거리를 구한다.
4. 3에서 구한 거리 중 가장 최소의 거리를 최종 거리로 선택한다.
5. 최종 점수 $f_q(v) = -d_{box}(q, v)$를 구한다.

5. Training

이제 지금까지 다뤄온 내용을 정리하고, 전체 학습과정을 살펴보자.
우선 우리는 입력값으로 query를 취하고, 출력값으로 노드를 가지는 모델을 다루고 있다. 이때, 정답 노드인 $v \in [q]$와 오답 노드인 $v' \not \in [q]$를 이용해 $f_q(v)$를 최대화하고, $f_q(v')$를 최소화하도록 진행할 것이다. 이때 모델 내부의 파라미터로는 다음과 같은 것들이 있다.

1. Entity embedding ($d|V|$)
2. Relation embedding($2d|R|$)
3. Intersection Operator(NN)

이제 주어진 그래프에서 어떻게 학습 데이터를 꾸리는지 살펴보자.

여기서 예시로 이전에 들었던 버락 오바마(anchor node), 국적(relation), 미국(answer node), 한국(wrong answer node)를 들어보자.

1. 랜덤하게 query $q$를 학습 그래프 $G_{train}$에서 추출하고, 해당 query의 정답 노드 와 오답 노드를 추출한다.
2. query $q$를 intersection operator를 이용해 임베딩 한다(최종 박스를 구한다.)
3. 정답노드와 오답노드에 대한 스코어 $f_q(v), f_q(v')$를 구한다.
4. $f_q(v)$를 최대화하고, $f_q(v')$를 최소화하도록 손실함수를 다음과 같이 구성한다.
   

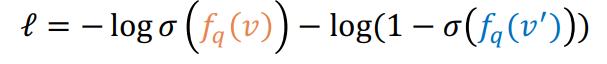
이때, query를 어떻게 만들까? query는 아래 그림처럼 종류도 다양하고, 그 크기도 다양하다. 모든 노드에 대해 정답으로 가지는 query를 학습시키지 않으면, 모든 노드에 대해 모델이 학습되지 않아 편향될 것이다. 어떻게 하면 각 query가 하나의 노드 씩 모든 노드를 정답으로 하도록 query를 구성할 수 있을까?

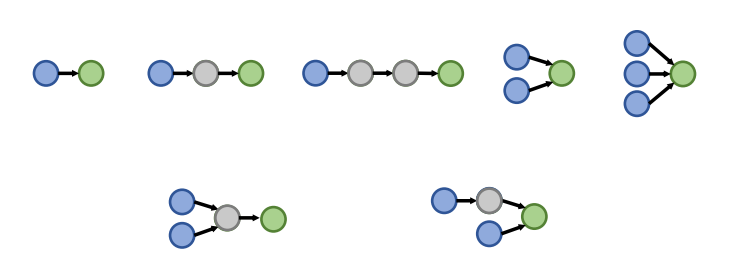
이는 query를 역으로 올라가면서 가능하다. 즉, 각 노드를 정답노드로 하고, relation을 거꾸로 올라가면서 query를 만드는 것이다.

1. 랜덤하게 지식 그래프에서 하나의 노드를 루트 노드로 선택한다.
   
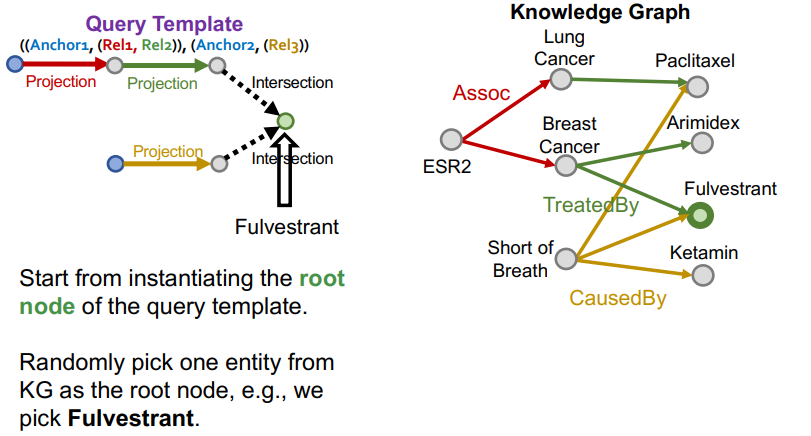
   여기선 Fulvestrant를 루트노드로 선택했다.

2. 랜덤하게 루트노드와 연결된 intersection을 선택한다. 그 intersection을 따라 relation을 기록한다.
   

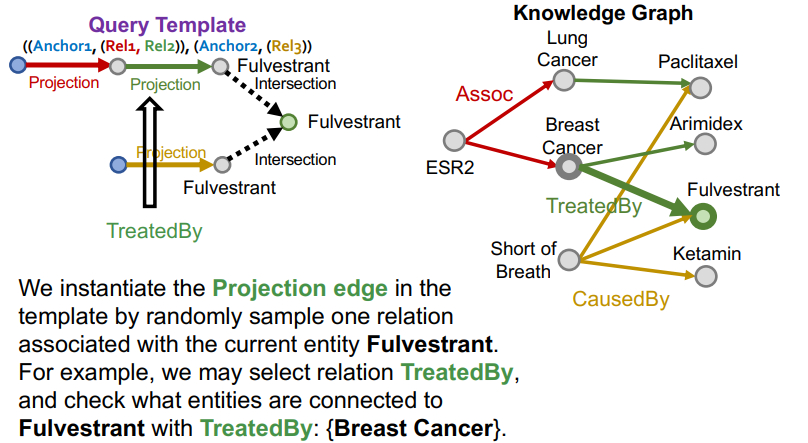
3. 이는 더이상 거슬러 올라갈 노드가 없을 때까지 relation을 거슬러 올라간다.
   

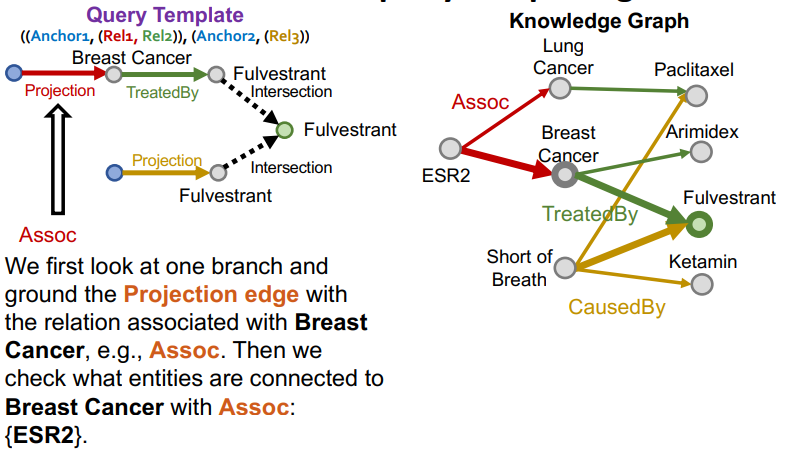
4. 2에서 선택하지 않았던 intersection에 대해 마저 relation을 구성한다.
   

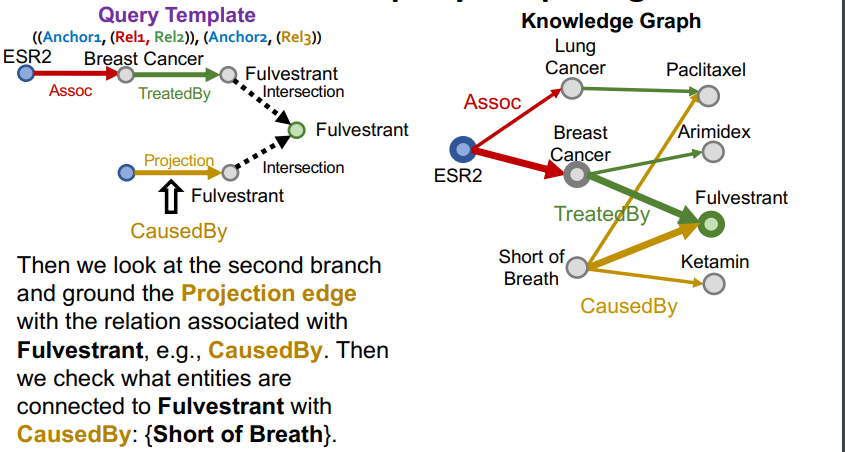
5. 이제 우리는 전체 query를 표현한 query template을 가지게 되었다.
   
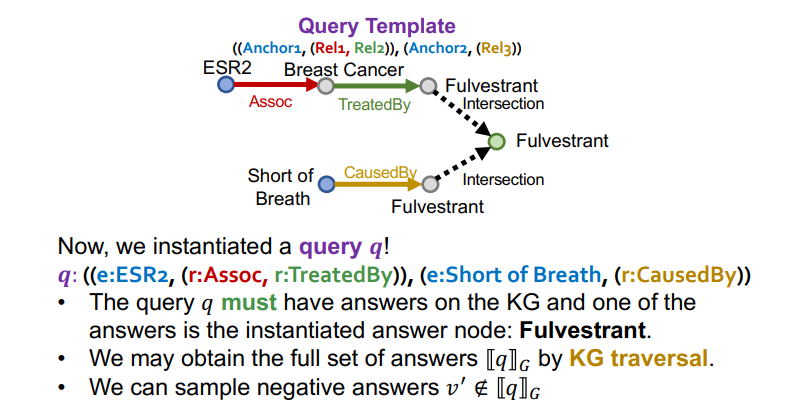
   이제 query template에서 전체 정답 집합을 구할 수 있다. 또한, 정답 집합 외의 오답 노드 역시 구할 수 있게 되엇다.

6. Visualization

실제 학습 과정을 t-SNE로 시각화 한 것을 보자.
질문은 다음과 같다.

List male instrumentalists who play string instruments

이를 query 형태로 표현하면 다음과 같을 것이다.

그리고 전체 임베딩 공간을 시각화 하면 다음과 같다.

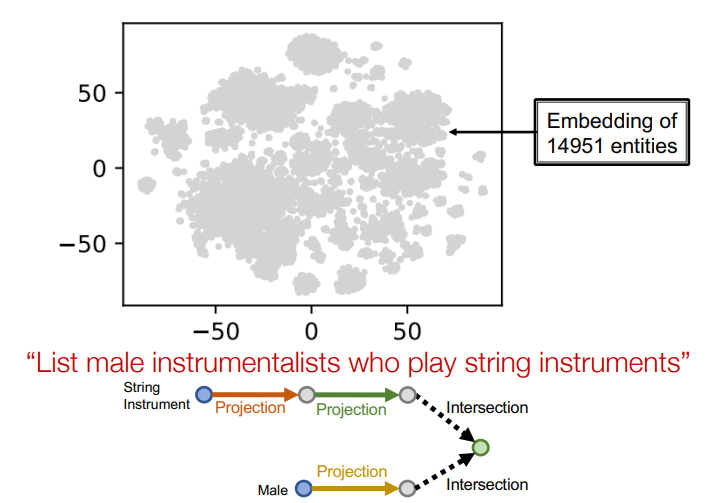
1. 첫번째 anchor 노드에서 시작
   

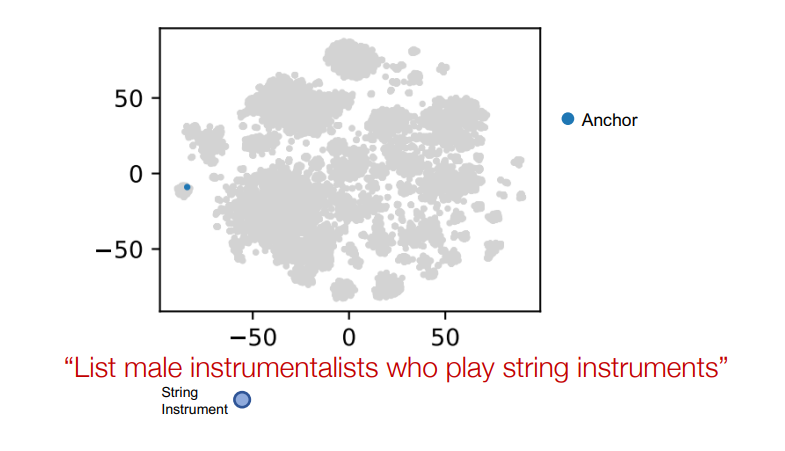
2. 첫번째 relation으로 이동
   
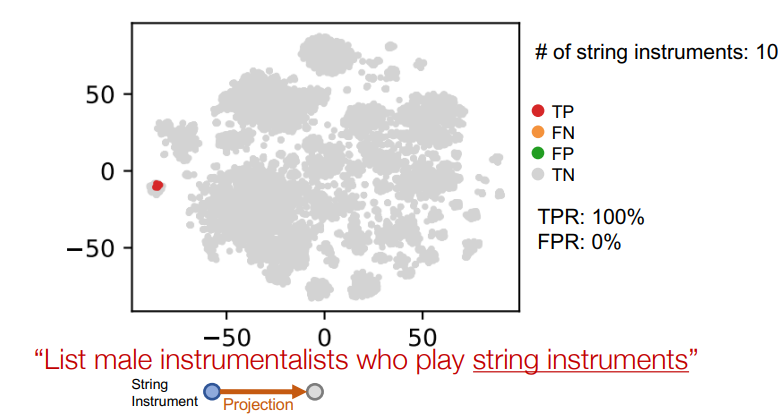
   이때 모든 정답 노드가 박스 안에 들어와서 TPR이 100%인 것을 볼 수 있다.

3. 두번째 relation으로 이동
   
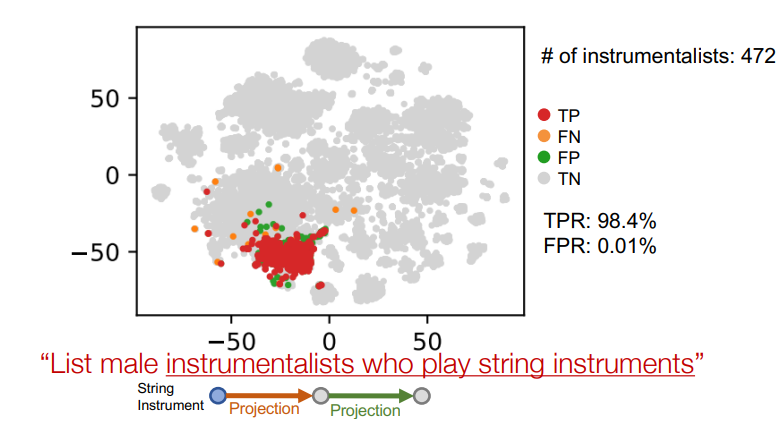
   이때 약간 박스에 오차가 생기면서 TPR이 낮아진 것을 볼 수 있다.

4. 두번째 anchor 노드에서 시작
   

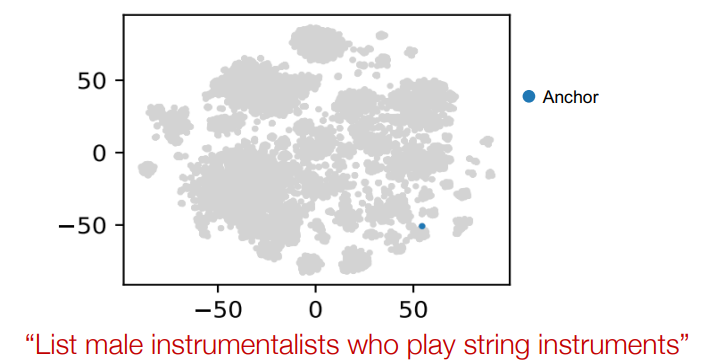
5. 세번째 relation으로 이동
   
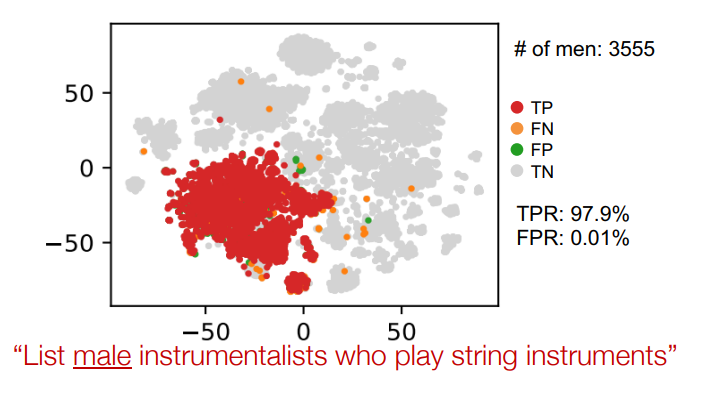
   이때, 남자 연주자가 무척 많다보니, 당연하게도 박스가 커지고 임베딩 공간에서도 크게 표시된 것을 볼 수 있다.

6. 3번과 5번의 박스를 intersection 함수에 삽입
   
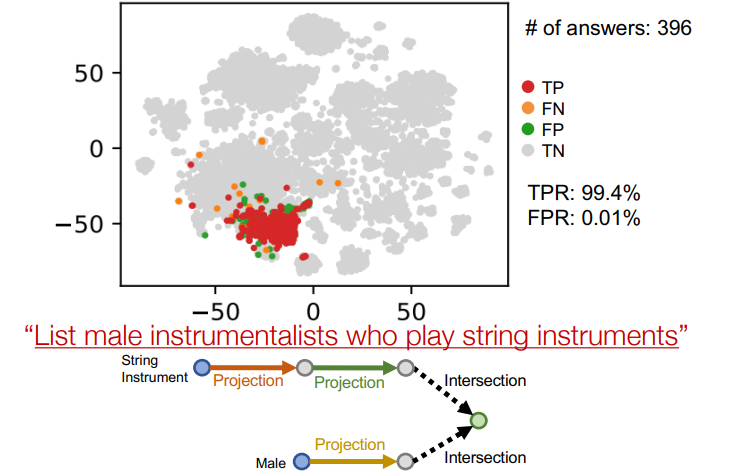
   그 결과 최종적인 박스가 구했다. 무려 99.4%의 TPR을 보인다.

7. Summary

요약하고 끝내자.

1. KG completion과 조금 다른 query 태스크에 대해 알아보았다.
2. TransE의 composition 성질을 이용하여 Path Query 태스크를 해결할 수 있음을 알았다.
3. TransE를 확장한 Query2Box를 이용해 and-or query 태스크를 수행하는 방법을 알아보앗다.
4. 임베딩 공간에서 최종적인 query 임베딩 박스 혹은 점은 정답 노드와 가까울 것이라는 것이 공통된 핵심 아이디어였다.