[작성자 : 권오현]

1. Community detection in network

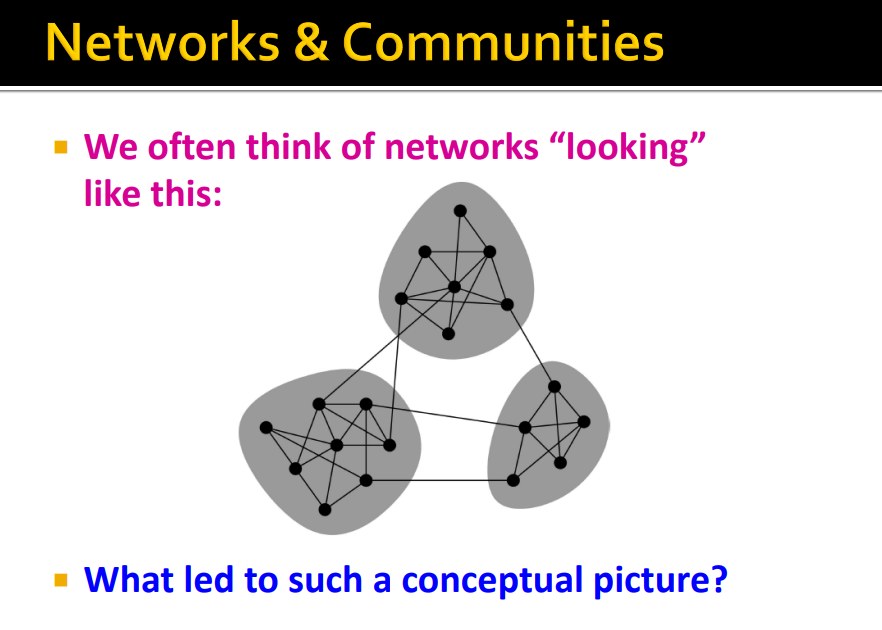
• Community Detection : Graph에서 nodes를 clustering 하는 것이다.

• 네트워크를 messy objects가 아닌 clustering, organization의 종류로 생각할 수 있음 (Following structure)

• Main Idea : 서로 간에 밀접하게 연결된 노드들의 집합, Cluster를 찾는 것이 목적

1.1 Granovetter's Answer

Community에 대하여 social science and classical social networks analysis 관점에서 생각해 보자

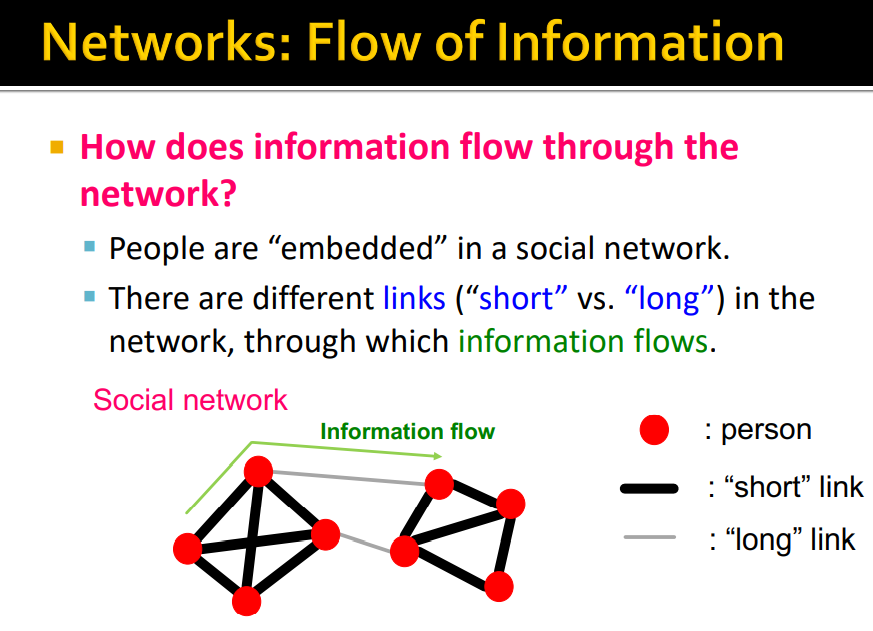
• Information flow
  • Short link : the ones that kind of are a very kind of local (strong friendships)
  • Long link : our acquaintances and kind of colleagues and people we meet less often

• Mark Granovetter는 '사람들이 새로운 직장을 어떻게 찾는지'에 대한 유형을 분석함
  $\rightarrow$ 사람들은 새로운 직장을 구할 때 친한 친구 보다 지인(Acquaintances)으로 부터 소개 받는 경우가 많다.
  

Granovetter's은 'Friendship'을 두가지 관점으로 바라볼 수 있다고 함(즉, link에는 두가지 관점이 있다.)

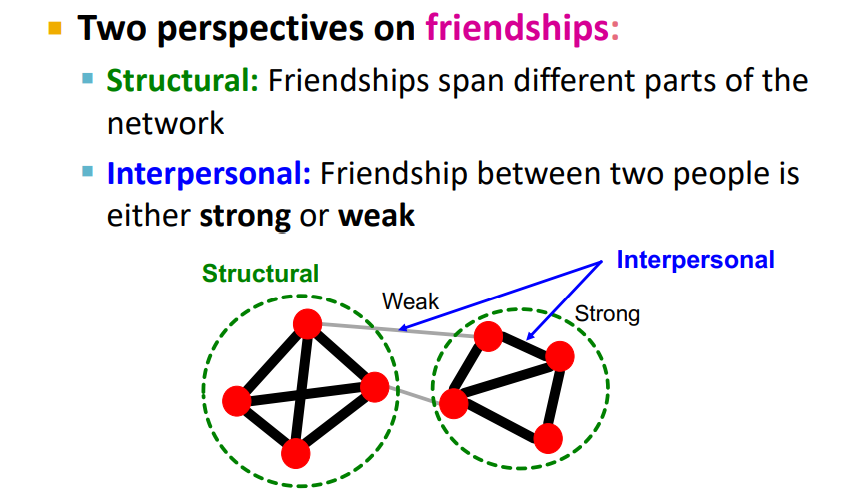
• Structural perspective : 링크가 네트워크의 어떤 부분을 연결하는가 ?
• Interpersonal perspective : 링크가 Strong or Weak ?

1.2 Granovetter's Explanation

Structural role - Traidic Closure = High clustering coefficient

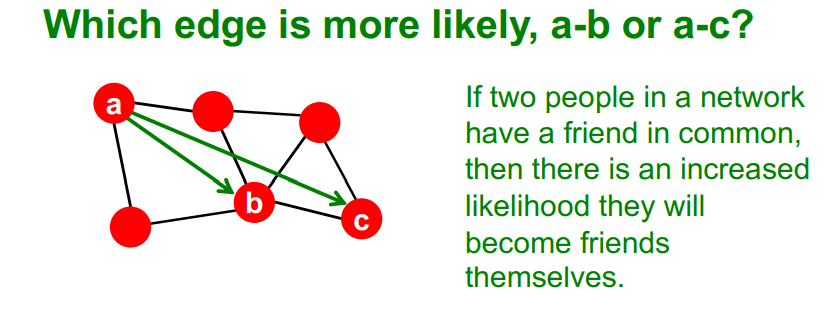
• a-c 보다 a-b가 더 연결될 가능성이 높은 edge이다. (두 명의 common nodes = High clustering coefficient)

  Teenage girls with low clustering coefficient are more likely to contemplate suicide

"Edge (Link)를 두가지 관저에서 바라볼 수 있다." - Structural role

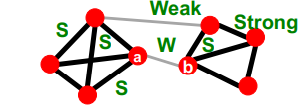
• First point : Structure
  • 구조적으로 강하게 연결된(tightly-connected) edges는 Socially strong
  • 네트워크의 다른 부분들에 걸쳐있는 edges(Long-range Edges)는 Socially weak

• Second point : Information
  • 구조적으로 연결된 edges는 Information access관점에서 매우 중복(redundant)
  • 다른 network와 연결된 edges(Long-range edges)는 더 많은 정보를 줄것이다. (other community에 접근할 수 있기 때문에)

1.3 Edge overlap

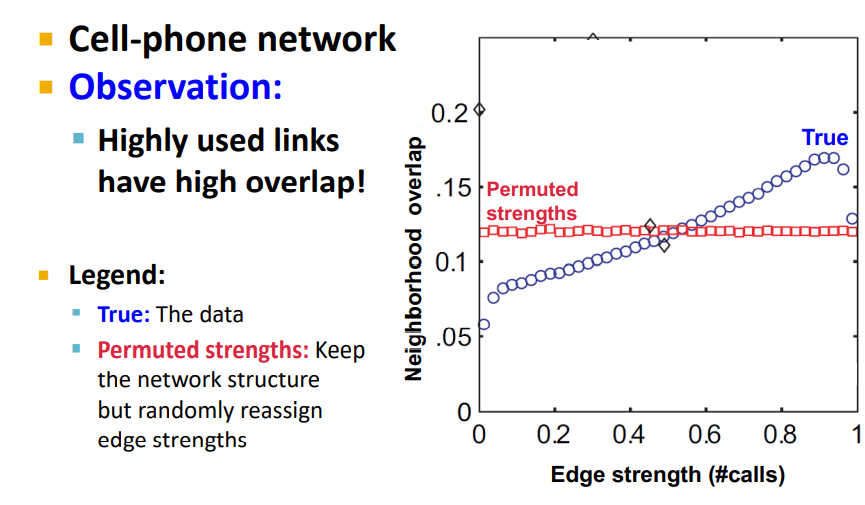
Grannovetter's theory는 1960년대에 제안되어 증명이 되지 않았지만 Onnela et al. 2007에서 Cell-phone networks를 통해 증명 되었다.

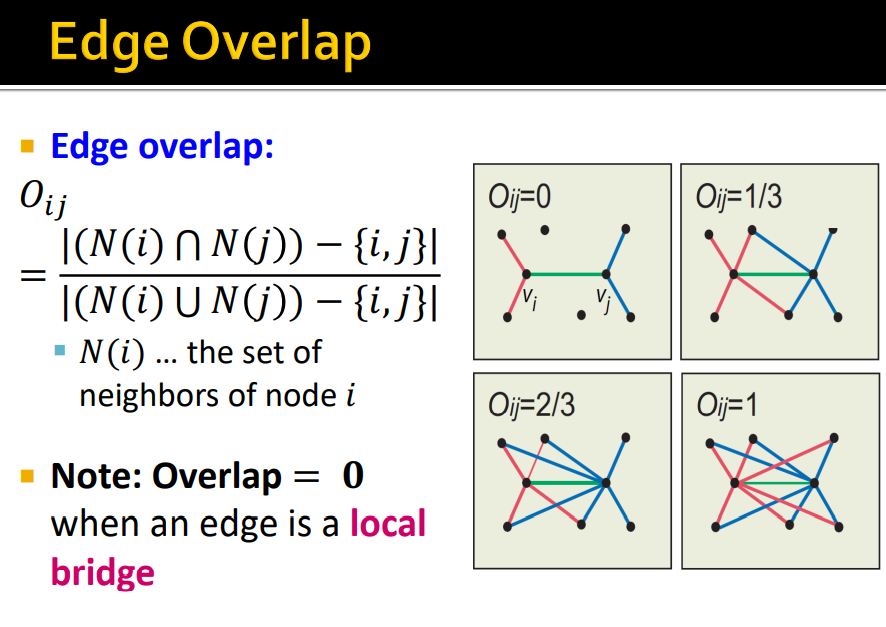
• 데이터 : EU 소속 국가 인구의 20% 휴대폰 네트워크 데이터

• Edge Weight는 통화 횟수

• Edge overlap : $O_{ij}$ - $i,j$의 node의 neigbors 중 얼마나 많은 지인(nodes)를 공유(overlap)하고 있는가에 대한 정보

• 결과적으로 통화 횟수(Inter-personal strength of friendship)가 많을수록 $O_{ij}$ 값이 커졌다.
  $\rightarrow$ Strong Edges를 가진 Communities가 존재한다.
  

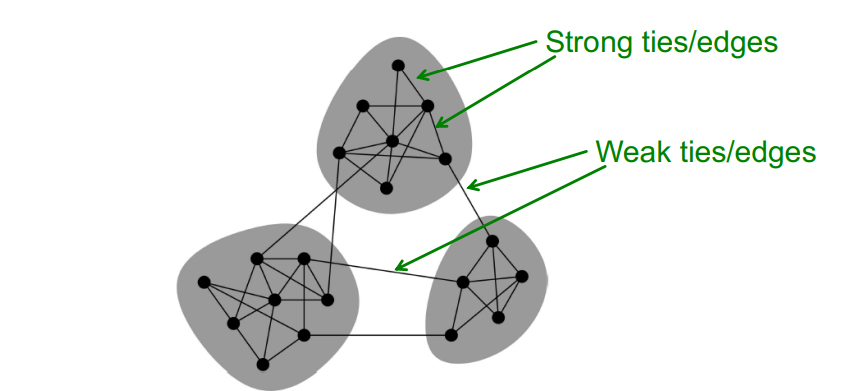
2. Network Communities

• Granovetter's theory에 의하면 Network는 tightly connected set of nodes !

• Network communities : Lots of internal connections and few external ones

(communities = clusters = groups = modules)

Networks에서 어떻게 densely connected groups of nodes(= tightly connected nodes)를 찾을 수 있을까 ?

$\rightarrow$ Modularity, Modularity를 Maximize하는 Communities를 찾으면 됨

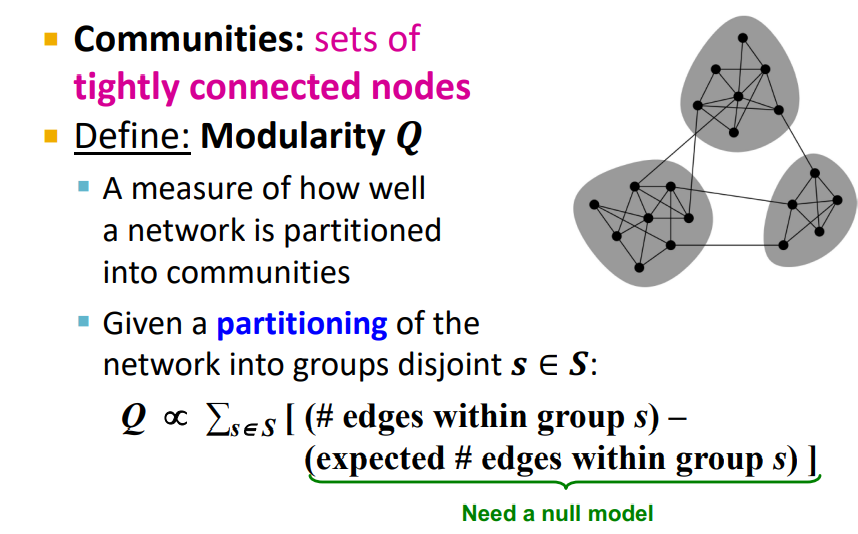
• Communities : set of tightly connected nodes

• Modularity Q : Network가 communities로 얼마나 잘 나누었는지(partitioning)에 대한 measure

• Partitioned된 Disjoint Communities S에 대하여 Modularity 계산

Q : "How many edges are within the members of the Group S - How many edges would I expect between this group S in random null model"
-> Null Model을 구하기 위해 subgraph mining을 배움 ex)Erdos-Renyi, configuration model

• Configuration Model :

  • Community가 잘 Partitioned 되어있는지를 평가하기 위한 rewired network(비교 network)

  • N개의 nodes와 M개의 edges가 주어진 Real Graph G를 통해 생성된 random network G'

  • Same degree distribution을 가지지만 uniformly random connections, multi graph

  • Expected number of edges

    $k_{i}$ : link to itself or whatever else
    $k_j/2m$ : 노드 $j$와 연결될 확률(i->j, j->i 이기 때문에)

  

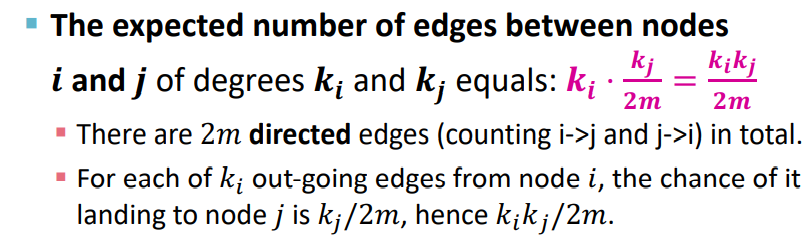
  • Expected number of edges in G' : All paires이기 때문에 2로 나누어줌
    

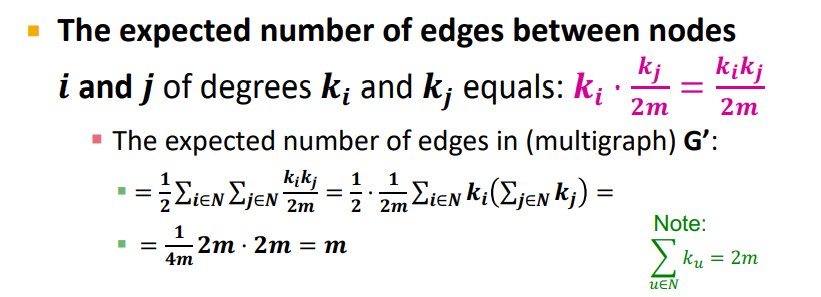
• Modularity 계산을 다시 나타내면 다음과 같이 됨
  

• Modularity q를 [-1,1]로 맞춰주기 위해 Normalizing constant

• 일반적으로 0.3 ~ 0.7 이면 Significant Community Structure
  

3. Louvain Algorithm

• Community detection을 위한 Greedy Algorithm ($O(n log{n}$) run time, n = number of nodes)

• Very scalable and popular algorithm

  "It's de facto thing you would use if you want to partition the network into a set of clusters"

• Scale to large networks, weighted graph and hierarchical communites 등 다양한 graph에서 사용 가능 ( one level에서의 clustering 뿐만 아니라 cluster의 kind of clustering도 제공한다)

• Fast implementation available, quickly and well in practice communities with high modularity
  

• Two phases 연산을 한다.

  • Phase 1 :

    • Graph의 nodes를 distinct community로 분류한다.(node마다 각각의 cluster, community를 가지게 된다.)

    • Node i를 Neighbor node j의 community와 합쳤을 경우의 modularity $\Delta Q$를 계산한다.

    • Neighbor node j의 communities들 중 가장 큰 $\Delta Q$를 발생시키는 community로 Node i를 이동

    • 위의 결과의 변화가 없을때 까지 반복

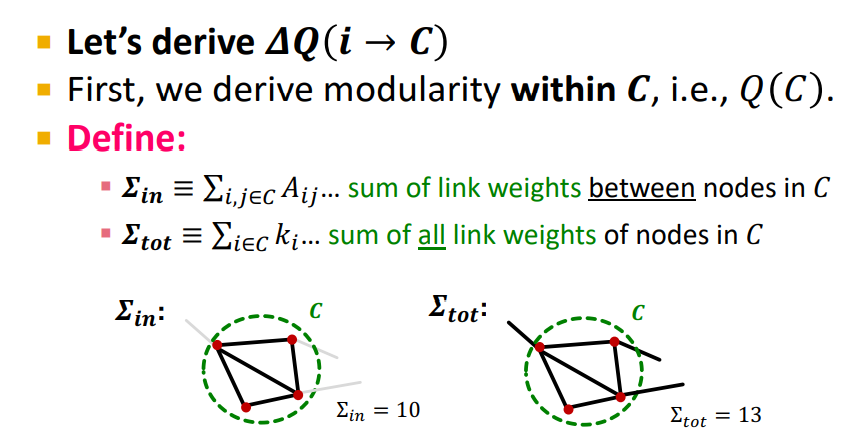
      $\Delta Q$를 구하는 방법은 다음과 같다.
      

    • $\Delta Q(i \rightarrow C$)를 구하기 위해 우선 C의 modularity $Q(C)$를 구해야 한다.

    • $\Sigma_{in}$ : Inside which is sum of the links, number of links or some of the link weights between the members of C

    • $\Sigma_{tot}$ : Ttotal number of links that all these nodes have
      

    • Modularity를 $\Sigma_{in}$, $\Sigma_{tot}$ 로 정리해 보면 다음과 같이 정리 된다.

    • $Q(C)$가 total links의 대부분이 within-community links일 때 가장 크다.

    $\Delta Q(i \rightarrow C$)를 구하는 것도 간단하게 구할 수 있다.
    

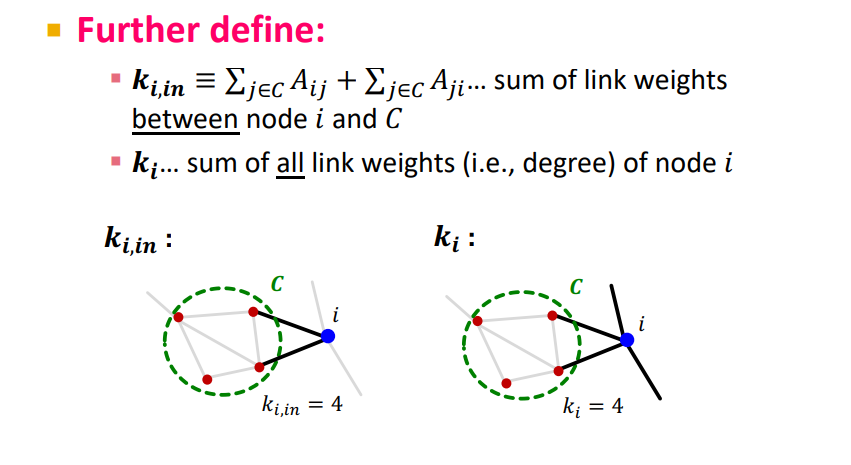
    • $k_{i,in}$ : the number of edges node i have to other members of c
    • $k_i$ : Total degree of node i

    

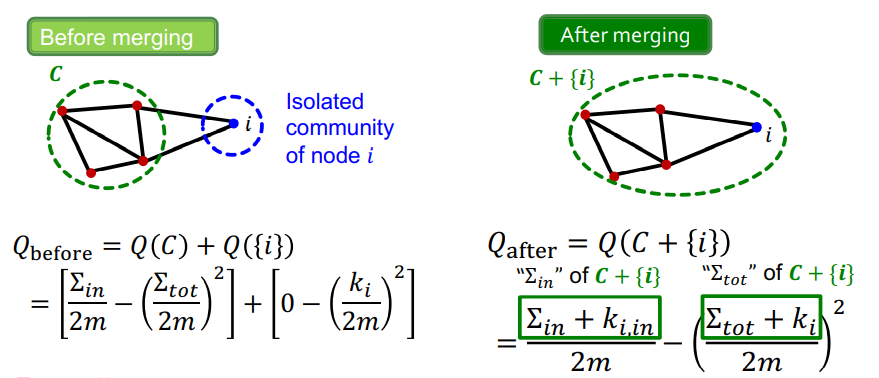
    • $Q_{before}$ : $Q(C)$ + isolated community i, isolated community는 number of edges inside가 0
    • $Q_{after}$ : number of edges inside $\Sigma_{in}$ increase by $k_{i,in}$

    

    • $\Delta Q(D \rightarrow i \rightarrow C$) 도 다음과 같이 구할 수 있다.
    • Nodes의 community가 움직이지 않을 때 까지 $C \rightarrow i \rightarrow C'$ 가 greedy way로 반복된다.

  • Phase 2(Restructuring) :

    • Phase 1에서 찾은 communities를 single Super-nodes로 Aggregate
    • Super-nodes는 communites를 구성하는 nodes 간에 적어도 하나의 edge가 존재하면 connected
    • 두 Super-node 간의 edge 가중치는 커뮤니티간 모든 edge 가중치들의 합
    • Super graph가 구해지면 phase 1을 다시 수행 (한 개의 Community를 찾을 때까지 반복)
      
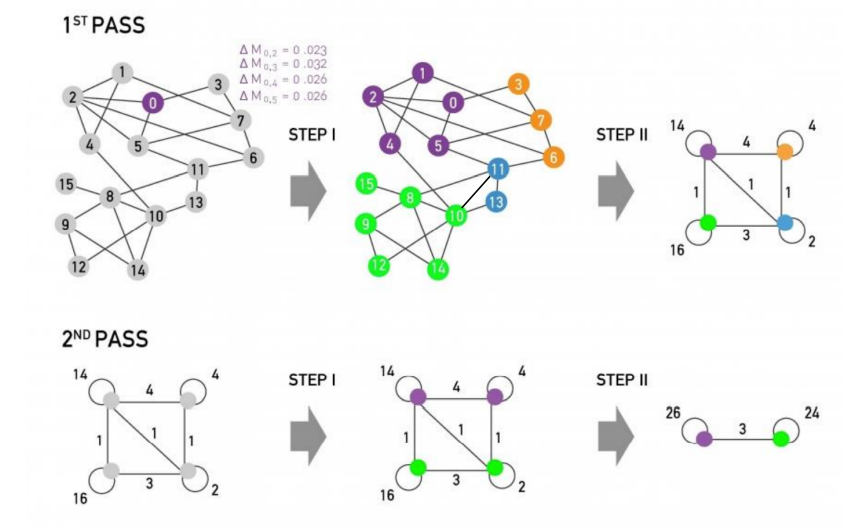
    • 위의 graph는 2개의 community, 4개의 community, 즉 hierarchical structure을 가질 수 있다.

4. Detecting Overlapping Communities : BigCLAM

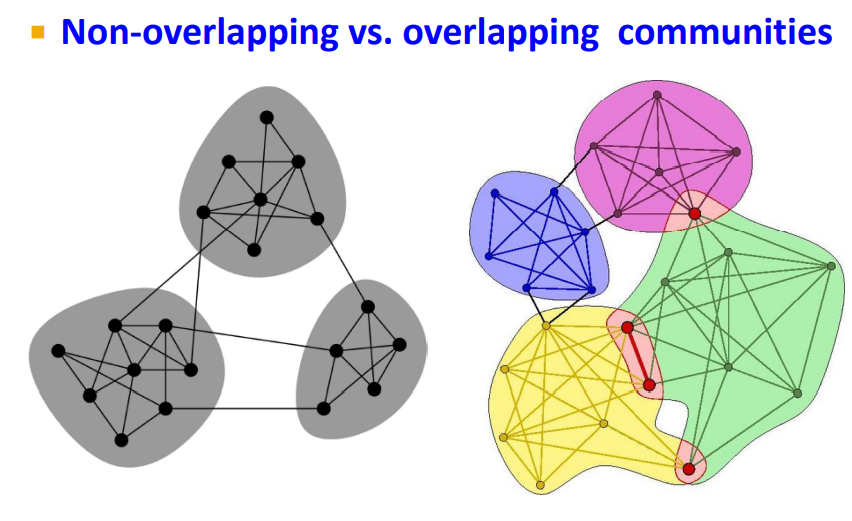
• 앞에서 Network structure에 대해 assumption을 정의하였다.

• Cluster : Each one has a lot of connection and then a few connection across

• 하지만 실제 세계에서 사람들은 multiple social communites를 가지고 있다. (overlap social structure)

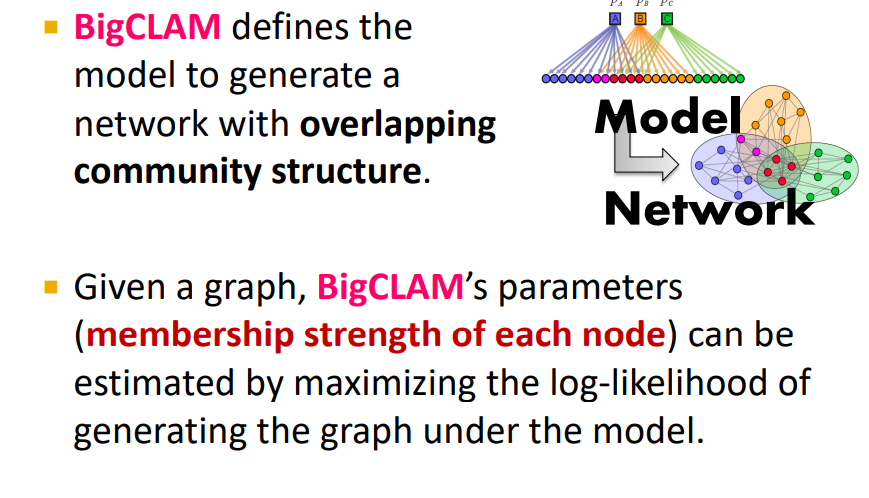
이러한 Overlapping community structure는 어떻게 Detect할 수 있을까 ? BigCLAM

4.1 BigCLAM

• Two Step
  • Step 1 :
    • Node community affiliation에 기반하여 Generative model을 정의한다.
    • Affiliation Graph Model (AGM))
  • Step 2 :
    • Graph G가 AGM을 통해 만들어 졌다는 가정
    • Optimization problem을 정의하여 best AGM을 찾는다.

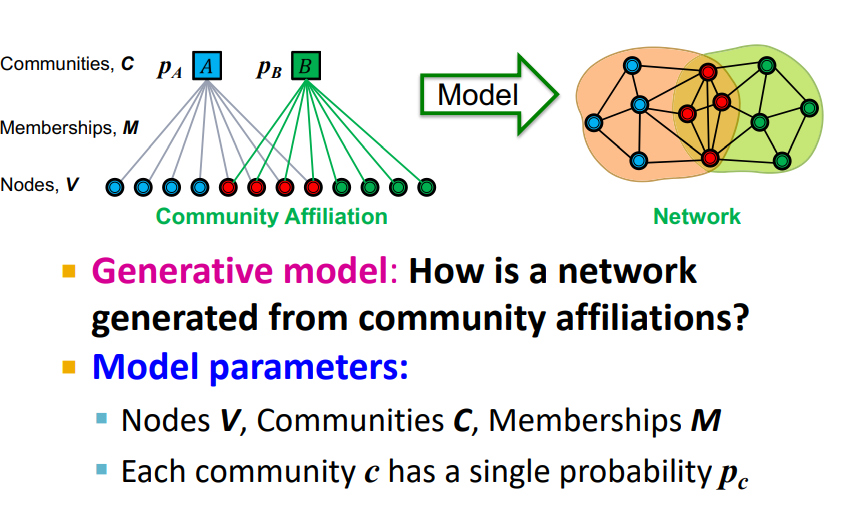
• 다음과 같은 형태로 Community Affiliation을 정의한다. 이를 통해 Edge of network를 생성하는 Model을 설정한다.

• Generative Model : Community affiliation으로부터 어떻게 네트워크가 generate 되는가 ?

Model Parameters :

• $V$ : nodes
• $C$ : Communities
• $M$ : Memberships
• $P_c$ : single parameters, Community C의 노드들이 서로 연결되어 있을 Likelihood

• $p(u,v)$ : u,v가 서로 연결되어 있을 확률
• 공통된 그룹의 수가 많을수록 연결될 가능성이 커진다.

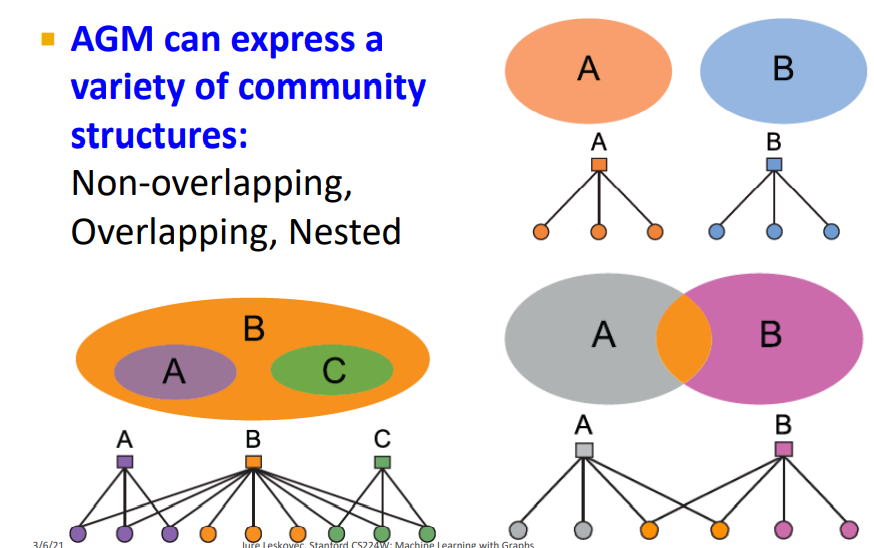
• 이러한 방식의 AGM은 다양한 Community structures를 만들 수 있다. (Non-overlap, overlap, hierarchical)

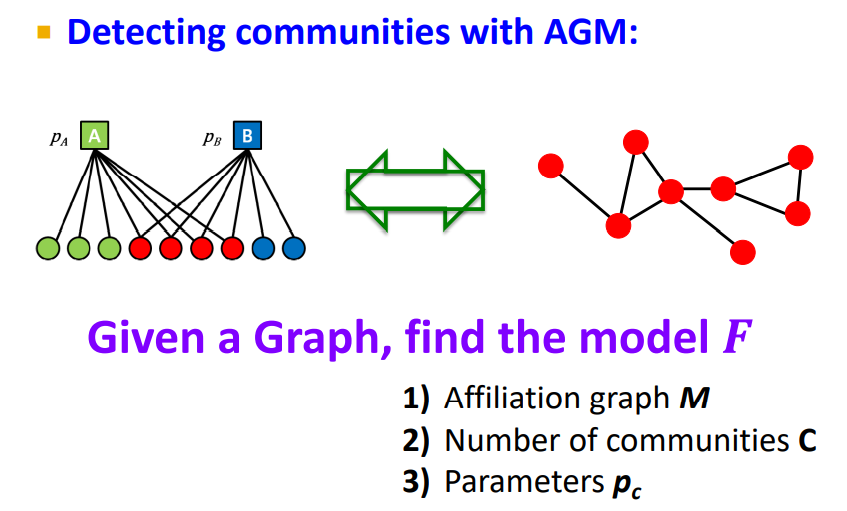
4.2 AGM

• 위의 내용은 Affiliation으로 Network를 만드는 방법에 대해 생각하였지만 Network,Graph 만으로 Model을 구할수는 없을까 ?

• Real-world graph는 AGM에 의해 생성되었다고 생각할 수 있다. 주어진 Graph를 가장 잘 생성하는 Model F도 찾을 수 잇을 것이다.

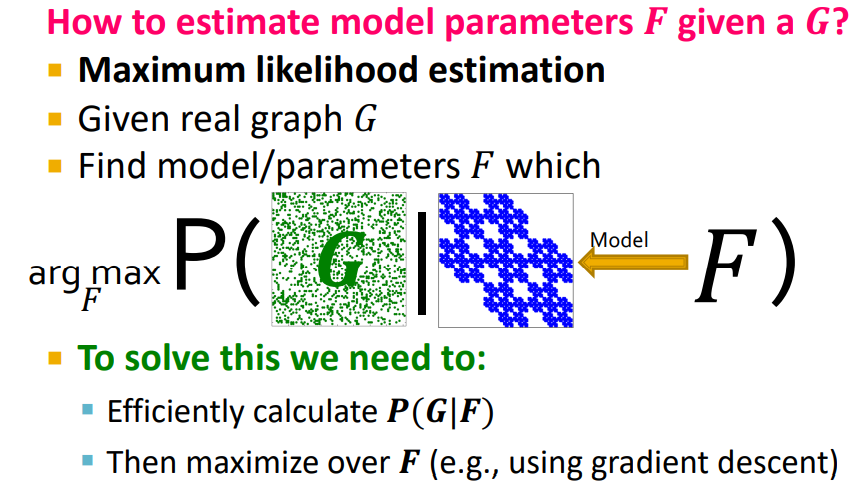
• Maximum Likelihood Estimation(MLE)를 통해 구할 수 있다.
  

• Model F를 통해 생성된 synthetic graph를 real graph와 비슷하도록 생성하고 싶다 !

• Model Parameter를 통해 Graph Probability를 측정할 수 있으면, 이를 argmax하는 F를 찾으면 된다.
  

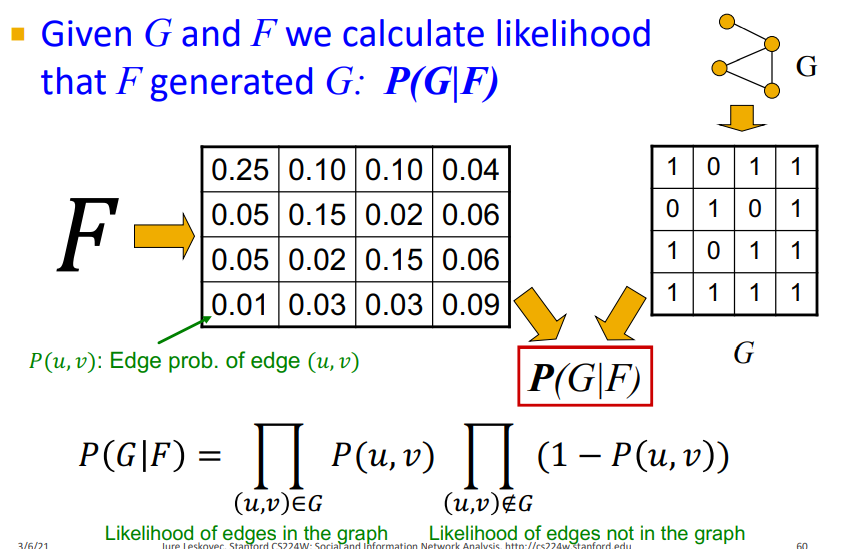
• Graph G와 model F가 주어 졌을 때, $P(G|F)$의 Likelihood를 구할 수 있다.

• adjacency matrix를 기반으로 Graph G에 대한 Probability를 assign한다.

• Edge가 연결될 확률을 잘 맞추고 Edge가 연결 안될 확률을 잘 맞춰야 함

4.3 "Relaxing" AGM

위의 모델은 0,1을 사용하여 노드들이 given community의 member인지 아닌지 따졌지만, 실제로는 overlaping communities기 때문에 모든 node community membership의 strength를 구해야 한다.

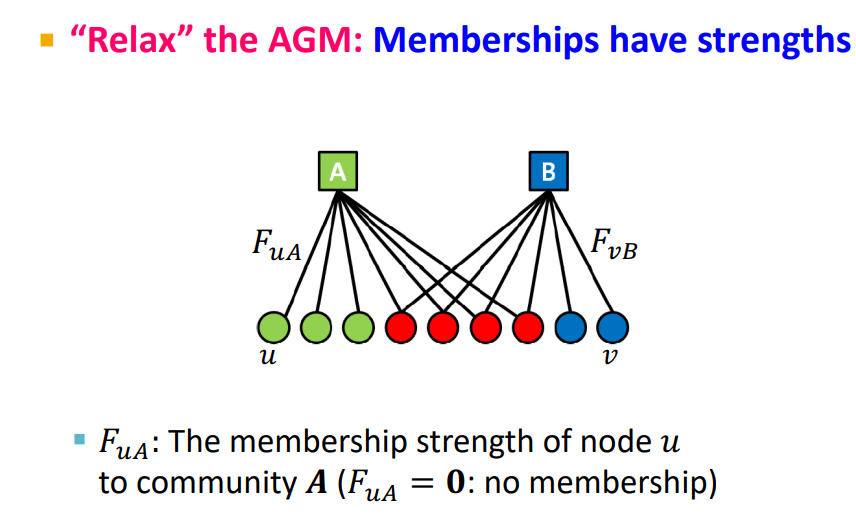
• 앞에서 각각의 communities가 parameters를 가지고 있고 여기에 대한 membership의 strength를 assign 하였다.

• $F_{uA}$ : community A에 대한 node u의 strength

• Community C에 대해서 node u와 v가 서로 연결되어 있을 probability $P_c(u,v)$

• Community C에 대한 node u의 strength $F_{uC}$, node v의 strength $F_{uV}$의 곱이 0 이면 $P_c(u,v)$, 크면 $P_c(u,v)$ 는 1에 가까워짐

• node u와v가 연결되어 있을 확률은 shared memberships의 strength에 비례

• 이러한 node u,v 는 여러 공통 communities를 가질 수 있는데 위의 식을 그대로 사용 할 수 있다.
  
  

• 다음과 같이 전개될 수 있는데, 결국 $F_{uC}$의 벡터들과 $F_{vC}$의 벡터들의 dot product가 된다.
  

• 위의 결과를 통해 community membership의 vector representation을 기반으로 pair of nodes의 probability를 정의할 수 있다.

• 결론적으로 $P(G|F)$의 likelihood 또한 다음과 같이 정의될 수 있다.
  

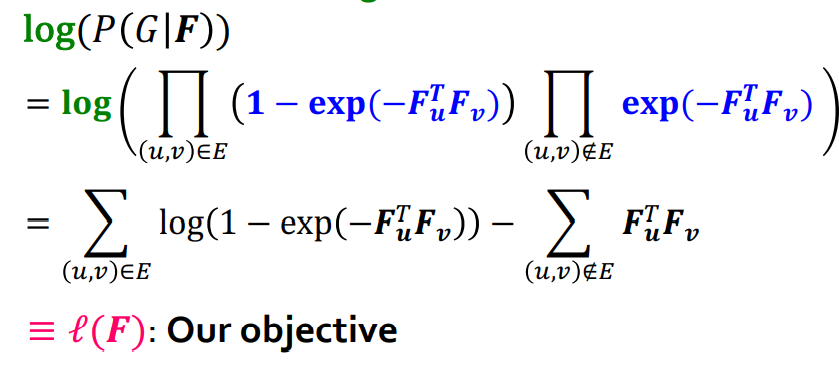
• 이를 Log-likelihood로 변환을 한다. ( log-likelihood를 optimizing하면 보다 더 numerical stability, Monotonic Transformation이기 때문에 동일한 position에서 maximize하는 것을 의미한다.)

• Objective function을 optimize하면 최적의 Model F를 찾을 수 있다.

• Log-likeihood를 increase하기 위해 gradient ascent를 통해 optimize 한다.

• 아래 식을 살펴보면 node u의 neighbors가 아닌 node v는 매우 많다.(Graph는 크고 연결된 neighbors가 별로 없기 때문에 전체 network에 대해 summation하는 것과 동일하다.)
  

• Gradient ascent는 느리지만 이를 다시 살펴 보면 다음과 같이 되고, 모든 nodes에 대해서 actually neighbors of node u만 빼주면 된다. (sum up over all the nodes를 저장한 후 나머지만 update하면 된다.)
  

Reference

CS224W
투빅스12-13 GNN 스터디
데이터괴짜 BLOG