작성자 : 김태욱

Contents

1. Community Structure in Networks
2. Network Communities
3. Louvain Algorithm
4. Detecting Overlapping Communities: BigCLAM

---

Community Structure in Networks

1. Community Structure in Networks

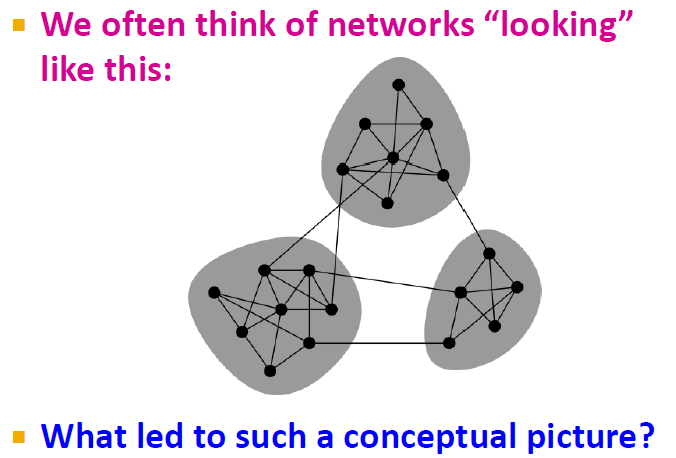
이번 챕터의 목적, 즉 Community Structure는 '서로간에 밀접하게(densely) 연결된 노드들의 집합을 구분하는 것'입니다.

알고리즘에 들어가기 전에, 사회과학적으로 군집이 생성되는 원리에 대해 먼저 보겠습니다.

Granovetter's Answer

Granovetter는 '사람들은 어떻게 새로운 직장을 찾는가?'에 대한 연구를 진행

-> 사람들은 자주 만나는 친한 친구가 아닌, 드물게 만나는 지인(Acquaintances)을 통해 직장에 대한 정보를 얻는다고 밝혔습니다.

이런 관계를 생각했을 때, 두 가지 관점의 frendships으로 나누어집니다.

• Structual: 링크가 네트워크의 어떤 부분을 연결하는가?
• Interpersonal: 링크가 강한 연결관계를 가지고 있는가 약한 연결관계를 가지고 있는가?

Triadic Closure

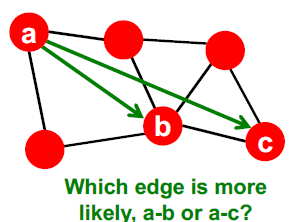
• 어떤 edge가 더 연결될 가능성이 높은가?

  답은 a-b입니다. a-c는 3칸 떨어져 있지만 a-b는 두 명의 공통된 이웃을 가지고 있기 때문에 a-b의 edge가 더 연결될 가능성이 높습니다.

Granovetter's Explanation

• First Point: Structure

  • 구조적으로 결속된(embedded) edge들은 사회적으로도 강하게 연결되어 있음.
  • 서로 다른 네트워크를 연결하고 있는(long-range) edge들은 사회적으로 약하게 연결되어 있음.

• Second point: Information

  • 구조적으로 결속된(embedded) edge들은 정보 접근의 관점에서 매우 중복(redundant)됨.
  • Long-range edge들은 지인(Acquaintances)들로부터 새로운 정보를 얻을 수 있게 됨.

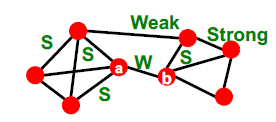
• S
  Structure: Socially Strong
  Information: Redudant
• W
  Structure: Socially Weak
  Information: Useful information

Edge Overlap

위의 이론은 Onnela에 의해 2007년 증명되었는데, 사용한 데이터는 EU 소속 국가 인구의 20%의 휴대폰 네트워크 데이터이며 Edge Weight는 통화횟수로 정의하였습니다.

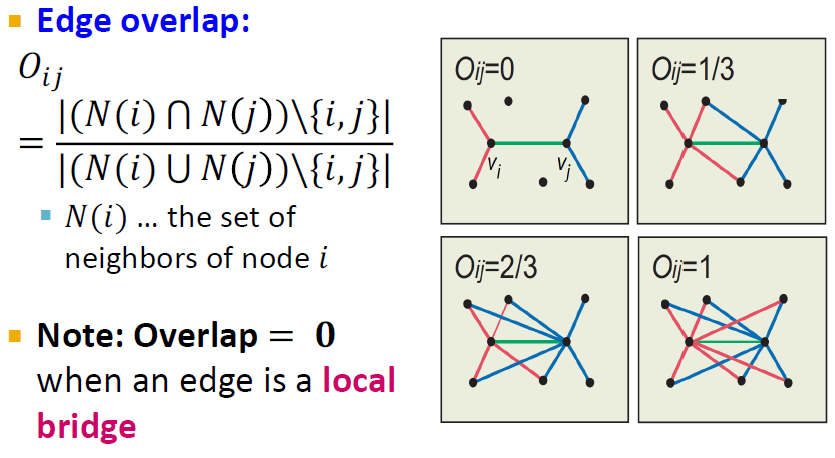
네트워크에서 얼마나 많은 지인(nodes)을 공유하고 있는가(overlap)에 대한 정보를 나타내는 수치를 Oij로 정의했습니다.
여기서 분자는 두 노드간의 겹치는 지인의 숫자이며, 분모는 두 노드의 모든 지인의 숫자(합집합)입니다.

즉, 지인을 공유할수록 해당 수치는 1에 가까워집니다.

2. Network Communities

Granovetter's의 이론에 따르면 네트워크는 강하게 연결된 노드의 집합(tightly connected sets of nodes)입니다.

• Network communities: 내부적으로 연결된 많은 노드와 몇몇 외부적으로 연결된 노드들로 이루어진 집합.

Modularity Q

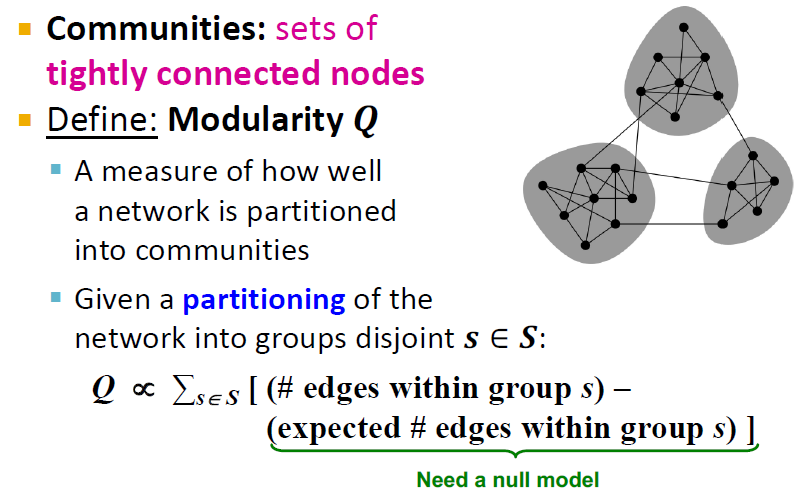
Communities는 강하게 연결된 노드들의 집합인데, 이 Communities를 찾기 위해 Modularity를 이용하며 이것을 최대화 하는것이 Communities입니다.

• Modularity Q란?
  네트워크가 communities로 얼마나 잘 나누어져(partitioning) 있는가에 대한 수치
• partitioning이란?
  하나의 노드가 어떠한 그룹(community)에 속하도록 네트워크를 쪼개는 것.

Q = community s의 edge 수 - 기대되는 community s의 edge 수
이 수치가 클수록(즉, edge수 차이가 클수록) 매우 strong group이라고 할 수 있습니다.

따라서, "기대되는 community s의 edge 수"를 찾기 위해 null model이 필요합니다.

Null model : Configuration Model

Real network G는 n개의 노드와 m개의 엣지를 가지고 있으며, 이를 이용해 rewired network G'을 만들 수 있습니다.

G'은 G와 같은 차수의 분포(degree distribution)를 가지고 있지만 uniformly random하게 연결되어 있으며, multigraph로 가정합니다.

노드 i, 노드 j의 degree를 $k_i, k_j$ 라고 할 때, edge의 기대값은 ${k_i} × {k_j \over 2m}$ 입니다.

${k_j \over 2m}$는 노드 j와 연결될 확률입니다. 또한 모든 노드는 2번씩 count되기 때문에 2m이 분모가 되며, multi-graph이기 때문에 노드 i의 degree인 ${k_i}$를 곱해주는 것입니다.

Modularity

• ${A_ij}$: 두 노드 사이의 edge 개수
• ${k_ik_j \over 2m}$: expected number of edges
• ${1 \over 2m}$: Normalizing constant

m개의 엣지를 가진 그래프가 가질 수 있는 엣지의 합이 최대 2m 였으므로, 2m으로 나눠줘 normalizing 해주면 Q는 -1과 1사이의 값을 가지게 됩니다.

또한 보통 0.3과 0.7 사이 정도면 Significant Community Structure가 있음을 의미합니다.

강의 중 질문에서 Q의 값이 negative일 때의 의미는 서로간에 거의 상관이 없는, 연결되어 있지 않은 community를 정의한 경우라고 합니다.(연결 되어야 하지만 연결되지 않은 경우)

Equivalently modularity는 위와 같이 표현될 수 있으며 ${c_i}$와 ${c_j}$는 노드들의 community입니다. $\delta(c_i,c_j)$는 indicator function으로 같은 그룹일시 1, 아니면 0 입니다.

3. Louvain Algorithm

Community detection을 위한 Greedy Algorithm이며, 시간복잡도 O(nlogn)으로 매우 빠른 휴리스틱 알고리즘 입니다.

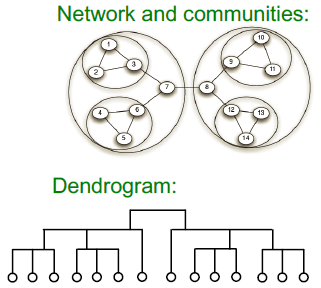
가중치 그래프도 지원하고, Hierarchical communities detection도 가능한데 이 경우 Dendrogram을 통해 네트워크의 Hierarchical한 구조를 나타낼 수 있습니다.

이 알고리즘은 빠르고, 수렴도 빠르고, High Modularity output을 도출해주기 때문에 네트워크에 널리 사용됩니다.

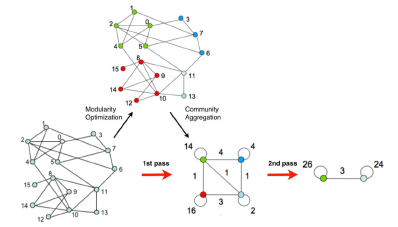
• Phase 1:
  • 가장 처음은 각각의 노드가 single community라고 생각
  • 노드 i를 어떤 neighbor j의 community 속에 넣으면 발생하는 modularity 값의 증가량(Modularity delta: $\Delta Q$)을 측정
  • 노드 i를, 가장 큰 $\Delta Q$를 발생시키는 community로 이동
  • $\Delta Q$의 변화가 없을 때까지 Phase1 계속 실행
• Phase 2:
  • Phase 1에서 찾은 community들을 모아 single super-node를 만들어 줌.
    • Super-node들 사이에 하나의 Edge라도 있으면 연결
    • 두 Super-node 간의 edge 가중치는 커뮤니티 간 모든 Edge 가중치들의 합
  • 다시 Phase 1으로(한 개의 Community를 찾을 때까지 계속 반복).

$\Delta Q(i→C)$ : 노드 i를 C community에 추가시켰을 때 Q의 증가량
$\Delta Q(D→i)$ : D community 에서 노드i를 제거시켰을 때 Q의 증가량
$\Delta Q$ = $\Delta Q(i→C) + \Delta Q(D→i)$

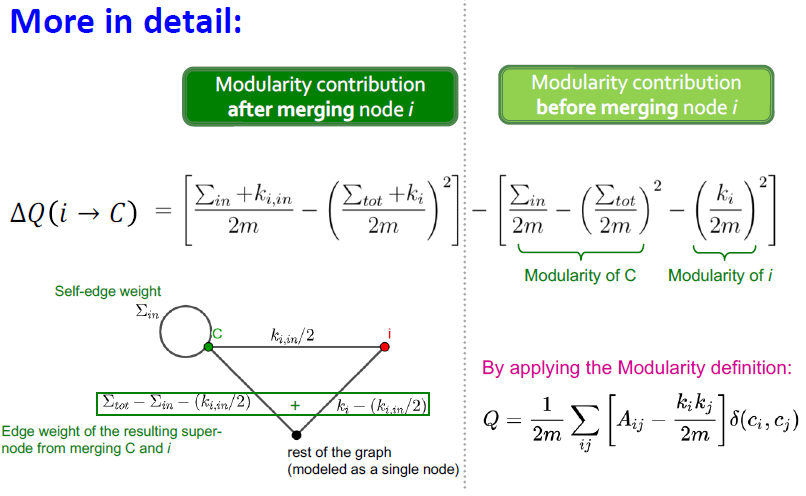
위의 그림은 $\Delta Q$식을 더 구체적으로 보여주는 내용입니다.

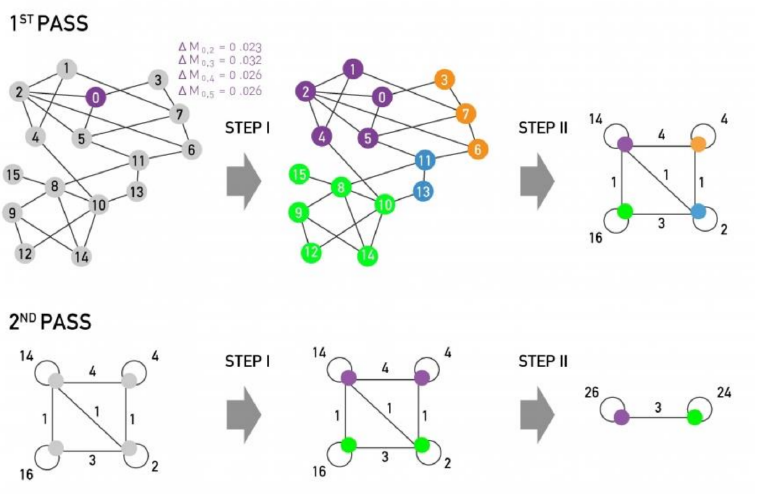
위의 그림은 Louvain algorithm의 전체적인 과정을 나타냅니다.

4. Detecting Overlapping Communities: BigCLAM

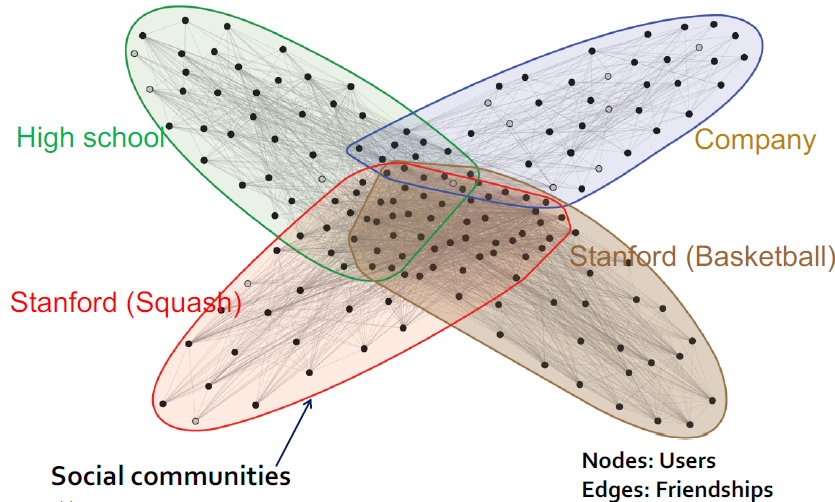
앞에서의 Community들은 모두 Non-Overlapping 이었지만 실제로는 고등학교 동창이면서 대학교 동창일수도 있는 것처럼 Community가 겹치기도 합니다. 여기서는 이에 해당하는 Overlapping Community를 Detect할 수 있는 방법을 알아봅니다.

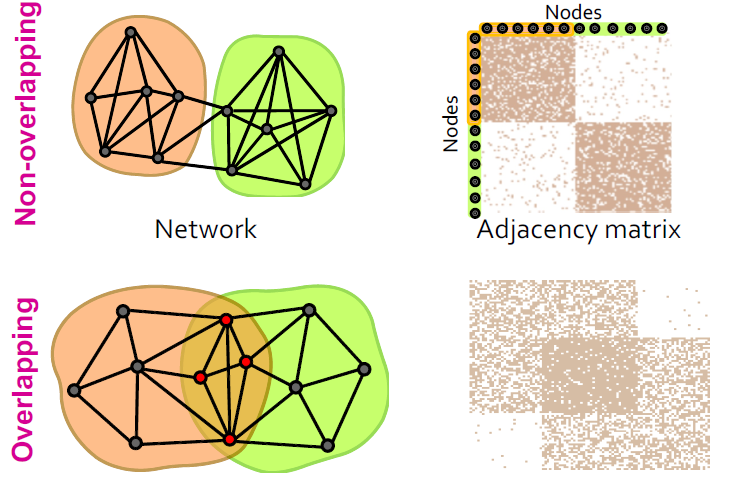
이는 인접행렬(adjacency matrix)에서도 확인할 수 있는데 만약 community가 discrete하다면 위의 그림처럼 겹치는(overlap) 부분이 존재하지 않을 것이며,
반대로 한 노드가 여러 community에 속할 수 있다면 아래의 그림처럼 겹치는 부분이 존재할 것 입니다.

마찬가지로 Overlapping Communities도 2가지 step으로 진행됩니다.

• Step1
  • Node Community affiliation에 근거하여 graph generative model을 정의
  • Community Affiliation Graph Model (AGM)
• Step2
  • Graph G가 AGM을 통해 만들어졌다는 가정 하에 진행.
  • AGM의 파라미터는 Graph G를 만드는데 사용되며, AGM이 G를 generative하도록 파라미터를 학습시킴. (MLE)
  • 여기서 파라미터는 node가 community에 얼마나 속하는지 알려줌.

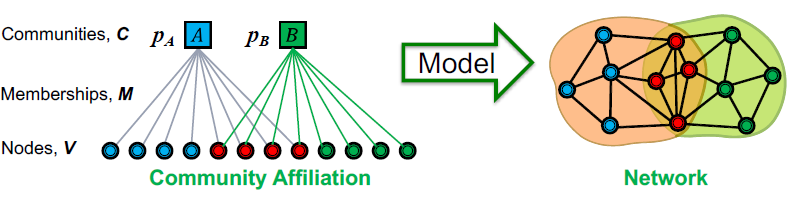
왼쪽 그림의 A, B는 communities이며, 밑의 점들은 네트워크 노드 입니다. community와 노드가 이어져 있다면 해당 노드는 해당 community에 속해있는 것이며, 양쪽 community에 모두 이어져 있다면 양쪽 모두에 속하는 것입니다.

이러한 Community affiliation가 모델을 거쳐 네트워크(오른쪽 그림)가 됩니다.

• Generative model issue: 어떻게 edges를 design할 것인가?

• Model Parameters: ${V, C, M, p_c}$
• $p_c$: 어떤 노드가 c community와 연결될 확률
• $M_u \cap M_v$: 노드 u, 노드 v의 공통 communities
• $p(u,v)$ : u,v가 서로 연결되어 있을 확률,
  1 - 두 노드의 공통 community에 속하지 않을 확률들의 곱
  -> 적어도 하나의 공통 커뮤니티에 속할 확률

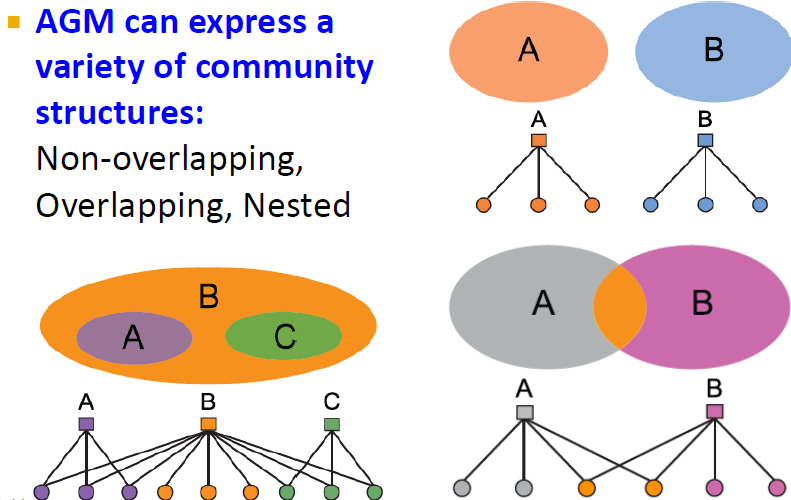
AGM은 Overlapping 양상에 따라서 다양한 Community Structure를 표현할 수 있음.

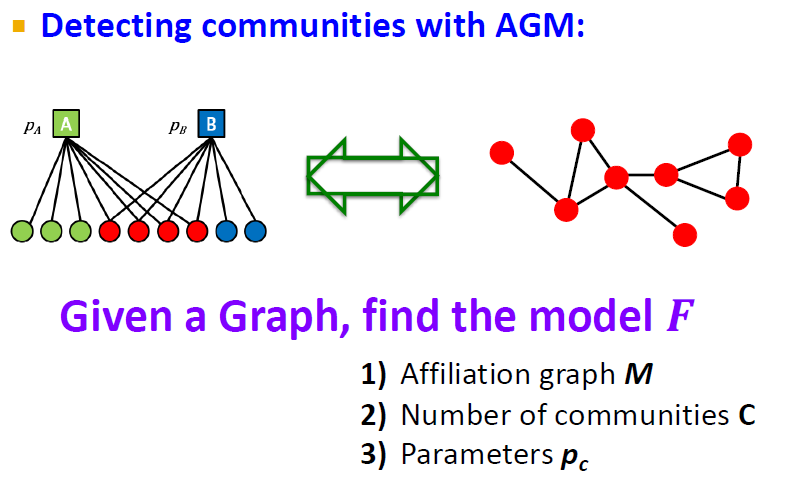
지금까지는 model로 네트워크를 생성했지만, 반대로 네트워크로 model(어떤 노드가 어떤 커뮤니티에 속하는지)도 만들어야 합니다.

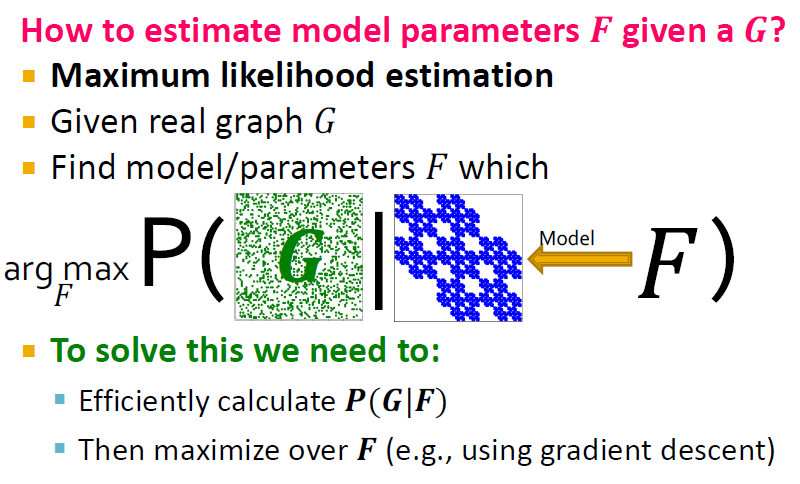
• Maximum Likelihood Estimation 사용
• F에서 생성된 network가 G이길 바라기 때문에 G를 잘 만들어낼 수 있는 F(model/parameter)를 찾으면 됨. -> real G와 가장 비슷한 G를 만들자!

이를 위해 F(model/parameter)가 주어졌을 때 G가 나올 확률(Graph Probability)을 구하고, 이 확률을 최대화(argmax) 시키는 F를 찾아야 합니다.

이것을 위해 우리는 (1) F가 주어졌을 때 G가 나올 확률을 구해야하고, 이 확률을 (2) 최대화시키는 F를 찾아야 한다.

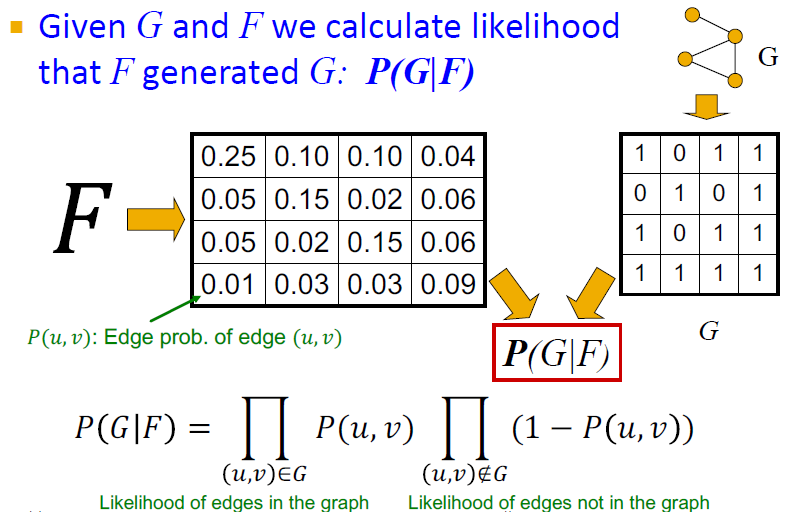
• Graph Likelihood $P(G|F)$ : F가 주어졌을 때 G가 나올 확률
• 오른쪽 행렬에서 $(u,v) ∈ G$ 일 때 1, $(u,v) ∉ G$ 일 때 0

"Relaxing" AGM: Towards P(u,v)

위의 모델은 0,1을 사용하여 노드들이 given community의 member인지 아닌지를 따졌지만, 여기선 모든 node community membership의 strength를 따져보기로 합니다.

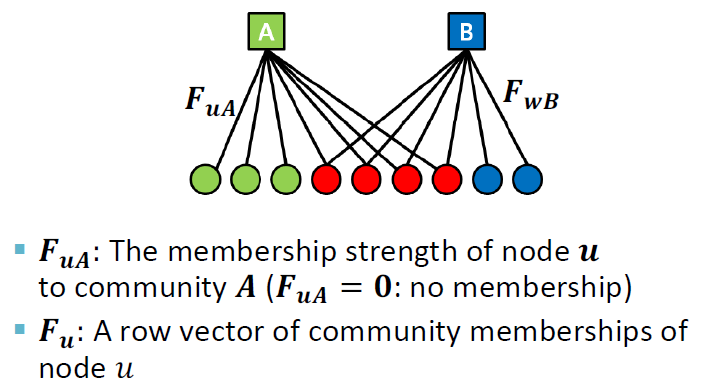
• $F_u$: 노드 u가 각각의 커뮤니티에 속할 확률을 가진 벡터
• $F_uA$: 노드 u가 community A에 속할 확률

• $exp(F_u·F_v)$: 노드 u와 노드v가 각각의 커뮤니티에 동시에 속할 확률 (하나의 노드라도 어떤 커뮤니티에 할 확률이 0이라면 둘의 product는 0)

노드 u와 v가 각각의 커뮤니티에 동시에 속할 확률은, shared memberships의 strength에 비례합니다.

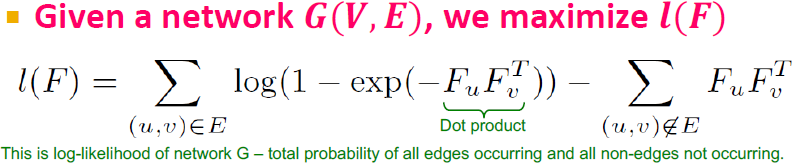
• $l(F)$: log-likelihood

결국 BigCLAM Model은 F가 주어졌을 때 G가 나올 확률을 구하고, 이 확률을 최대화시키는 F를 찾고자 하는 것입니다. 즉, log-likelihood를 최대화 하는 F를 찾는 것입니다.

Reference

https://tobigs.gitbook.io/tobigs-graph-study/chapter4.-community-structure-in-networks
https://data-weirdo.github.io/data/2020/09/05/data-graph-04.communities