작성자 : 장아연

Aggregate Neighbors

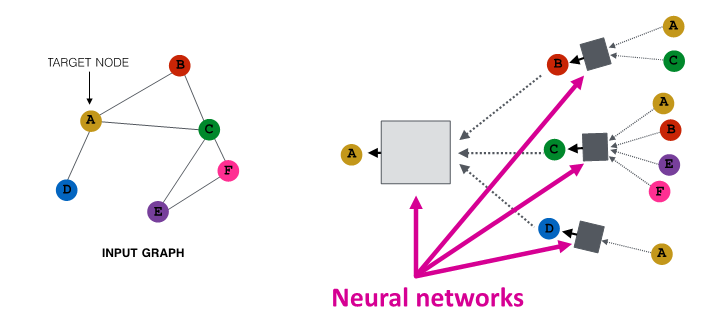
• local network neighborhood를 바탕으로 node embedding 생성
• node는 neural network 이용해 neighbor로부터 aggregate information

GNN Model

• 서로 다른 GNN model은 서로 다른 neural network를 사용
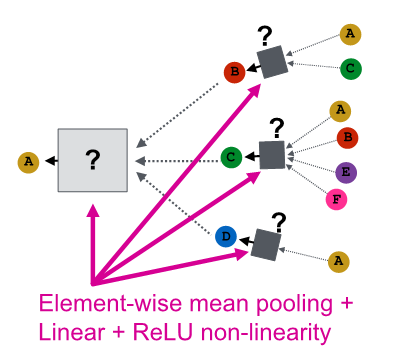
  GCN (mean - pool)

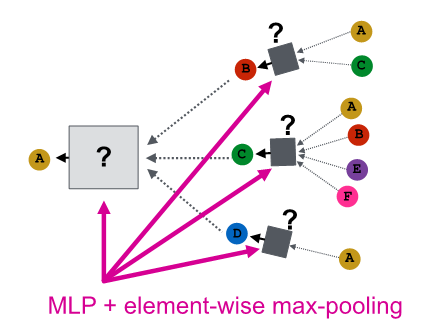
GraphSAGE (max - pool)
  

Local Neighborhood structure

Note : Node Color
use color to represent node feature
-> same color = same feature representation

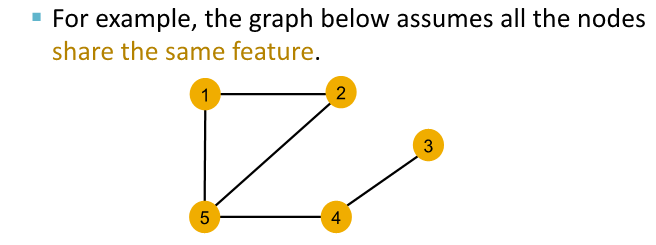
Can GNN distinguish different graph structure?

• quantify local network neighborhood around each node

easy to distinguish

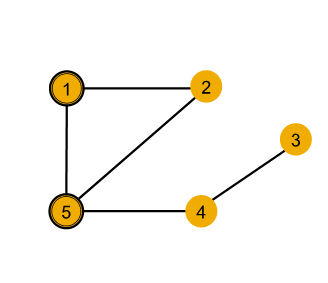
node	single hop neighborhood
node 1	degree of 2
node 5	degree of 3

case 1 : hard to distinguish

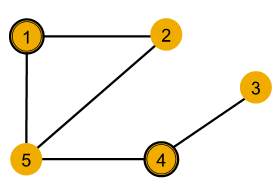
node	single hop neighborhood	second hop neighborhood
node 1	degree of 2	degrees of 2 (node 2) and 3 (node 5)
node 4	degree of 2	degrees of 1 (node 3) and 3 (node 5)

case 2 : can not to distinguish

• symmetric within graph
  

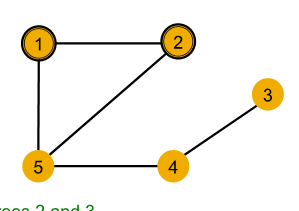
node	single hop neighborhood	second hop neighborhood
node 1	degree of 2	degrees of 2 (node 2) and 3 (node 5)
node 2	degree of 2	degrees of 2 (node 1) and 3 (node 5)

go steep deeper to 2nd hop neighbor, still have same degree

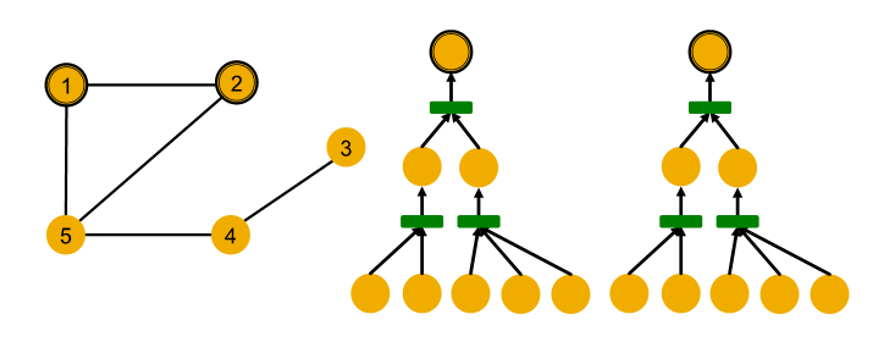
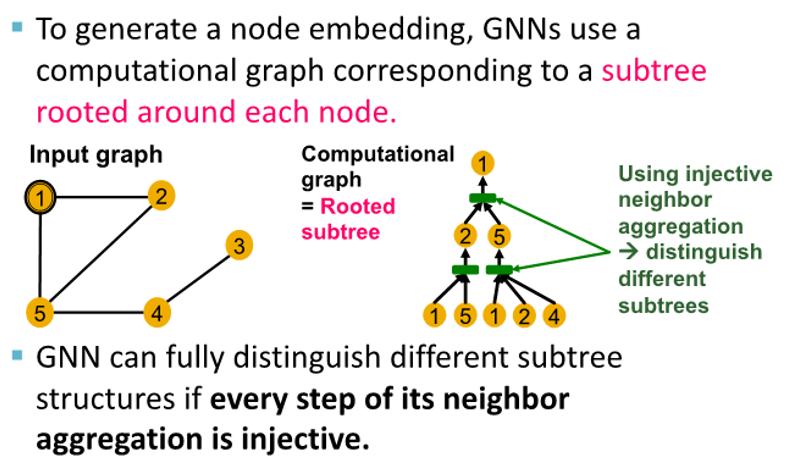
Computational Graph

• GNN aggregate neighbor node embedding
• define neighborhood
  -> use computation graph
  -> then GNN generate node embedding

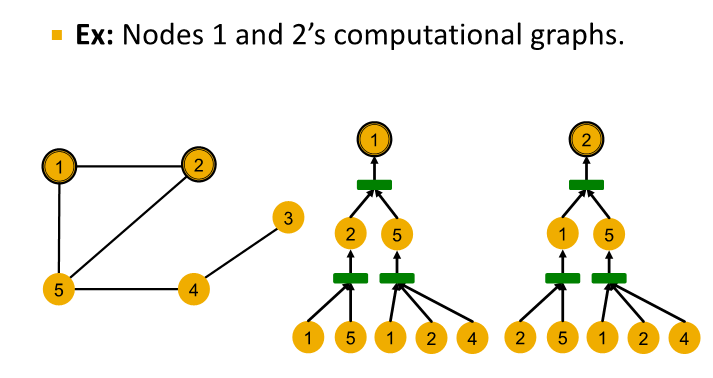
• Node 1's commputational graph (2-layer GNN)
  level 0 : (node 1, node 5) , (node 1, node 2, node 4)
  level 1 :
  node 5 aggregate information from (node 1, node 2, node 4)
  node 2 aggregate information from (node 1, node 5)
  level 2 :
  node 1 aggregate information from node 2 and node 5

• GNN은 message passing information without node ID, only use node feature

• computation graph of two node are same
  -> embedded exactly into same point in embedding space

• GNN generate same embedding for node 1 and node 2
  why ?
  1. computational graph are same
  2. node feature are same

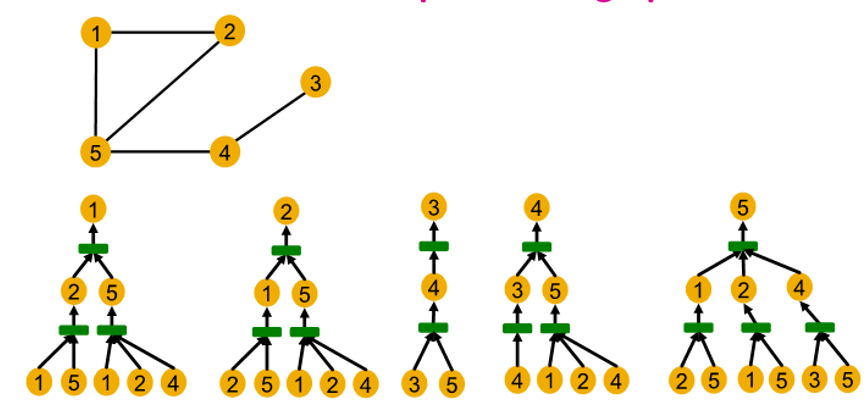
• Computational graph are identical to rooted subtree structure for each node
• Rooted subtree structure
  : recursively unfolding neighboring node from rooted nodes

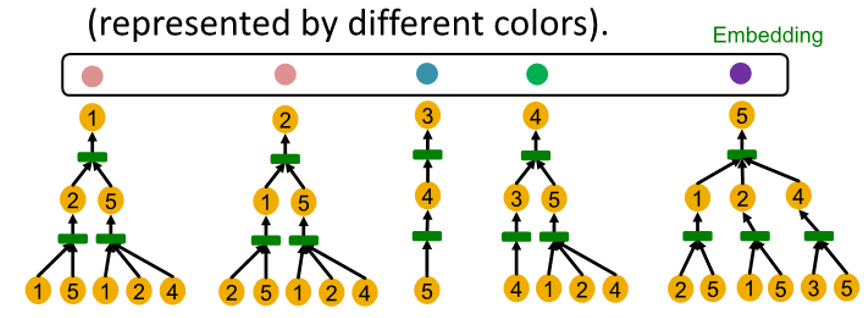
• GNN은 rooted subtree structure 포착해 이에 따른 node embedding 매핑

How expressive is a GNN?

Injective function

• $f$ : $X$ -> $Y$ : 서로 다른 X에 대해 서로 다른 Y 매핑
• $f$가 input $X$에 대한 모든 결과값을 가짐
  

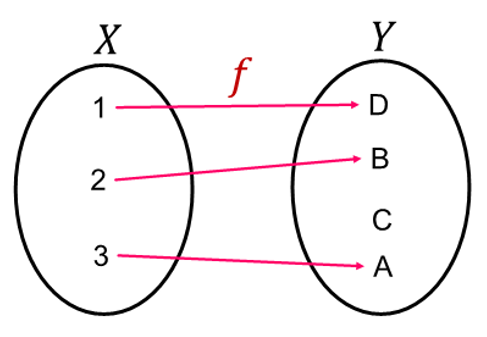
GNN map subtree to node embedding injectively

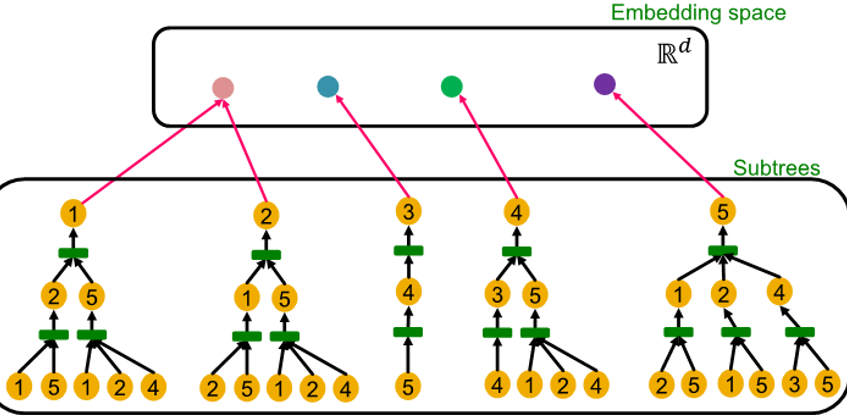
Most Expressive GNN : use injective neighbor aggregation

• same depth subtree : recursively characterized from leaf to root node
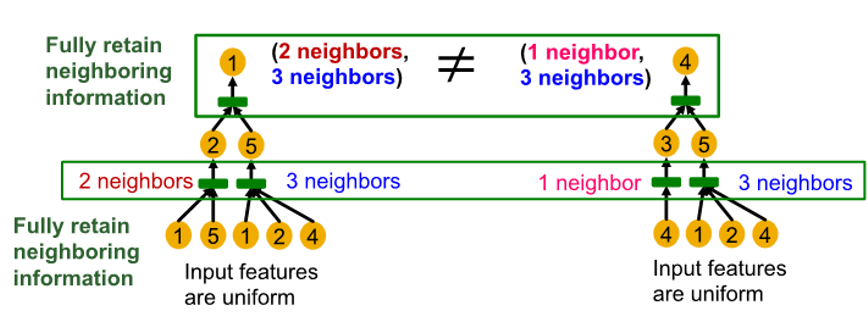
• Injective neighbor aggregation :
  서로 다른 neighbor -> 서로 다른 embedding
  ( GNN aggregation에서 neighborhood information을 완전히 얻는 경우, 생성된 node embedding은 서로 다른 rooted subtree 구별 가능 )

Neighbor Aggregation

• GNN 표현력은 사용하는 neighbor aggregation function에 따라 좌우됨

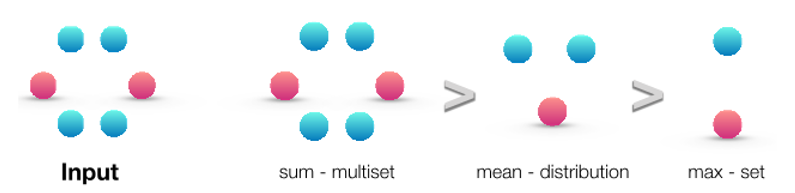
Neighbor Aggregation : a function over multi-set

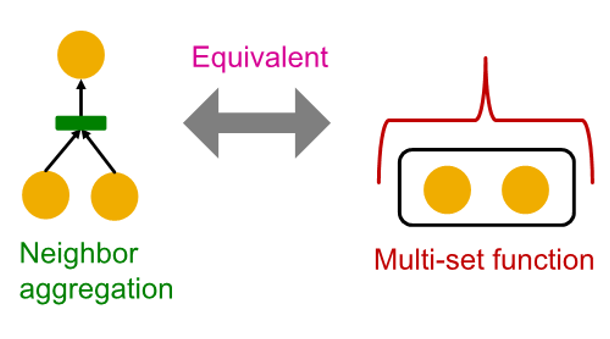
neighbor aggregation
: node and aggregated from two neighbor for two children
Multi-set function
: set of children (two yellow) and need to aggregate information from that set

Aggregation function for GNN model

GCN (mean-pool)

• element wise mean -> linear function -> Relu activation
  
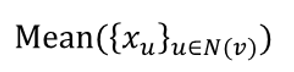
• same color proportion의 multi-set 구별 불가능
  
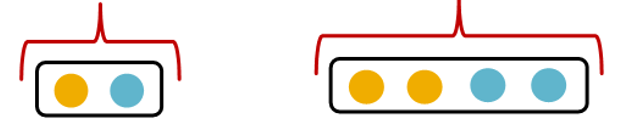
• failure case example
  represent node color by one-hot encoding
  

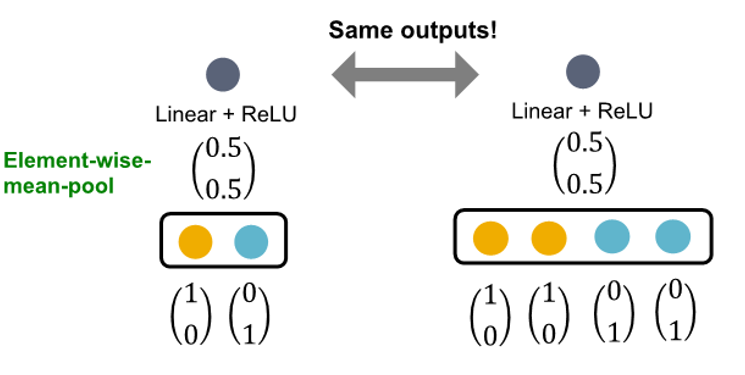
GraphSAGE(max-pool)

• element wise max pooling
  
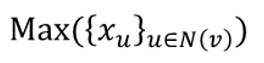
• same distinct color set의 multi-set 구별 불가능
  
• failure case example
  
  
  

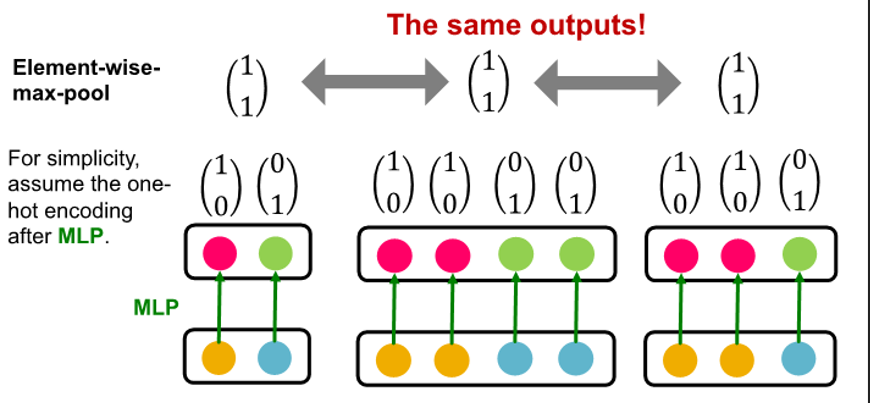
not injective : fail to distinguish some basic multi-set
not maximally powerfull GNN
need to design neural network that can model injective multiset function

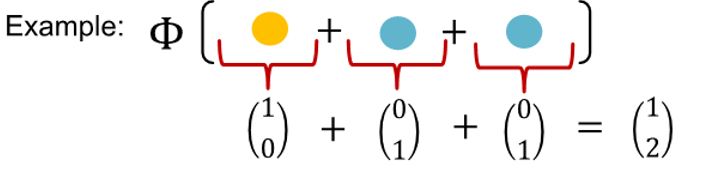
Injective Multi-Set Function

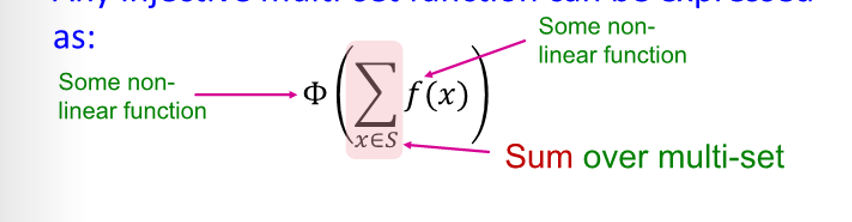
• $f$ produce one-hot encoding of color
• summation of one-hot encoding retain all information about input multi-set
  

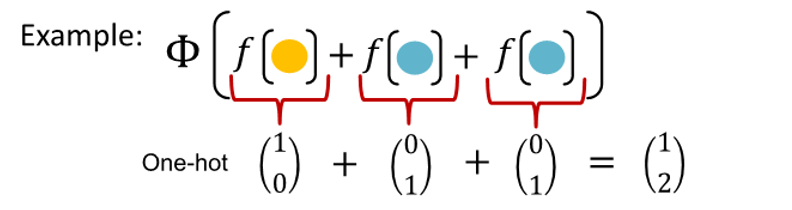
Universal Approximation Theorem

• use MLP(Multi-layer perceptron) to model $\Phi$ & $f$
• large hidden dimensionality 1-hidden layer MLP and non linearity
  -> continous function을 arbitrary accuracy로 근사 가능
  (hidden dimensionality는 100~500 정도가 적절)

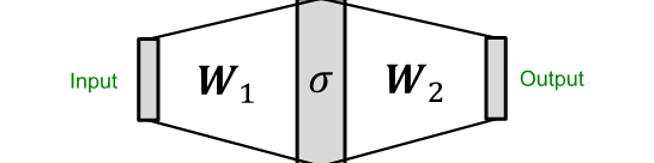
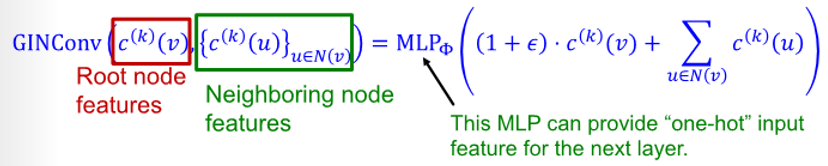
The Complete Graph Isomorphism Network Model

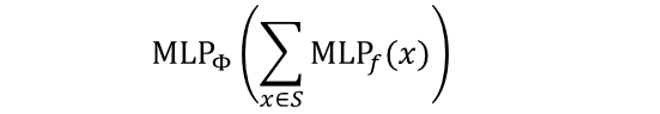
• take multi-set with element $x$ -> apply multi-layer perceptron -> sum up -> apply another perceptron
• multi-layer perceptron은 임의의 함수에 근사하고 이로서 $f$와 $Phi$에도 근사됨
• GIN의 neighbor aggregation function은 injective함
  GNN에서 가장 표현력이 좋음 & 실패 사례 없음

Full model of GIN with relation to WL Graph Kernel
color refinement algorithm in WL kernel

• initial color : $C^{(0)}(v)$ to each node
• interatively refine node color
  
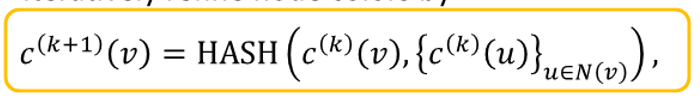
  to create color at k+1 for given node
  -> take color of node $u$ that are its neighbor from previous iteration
  -> then, take node $v$ from previous iteration
  -> after, hash two colors
• after $K$ color refinement, $c^{(K)}(v)$는 $K$-hop neighborhood의 구조를 요약함

Example

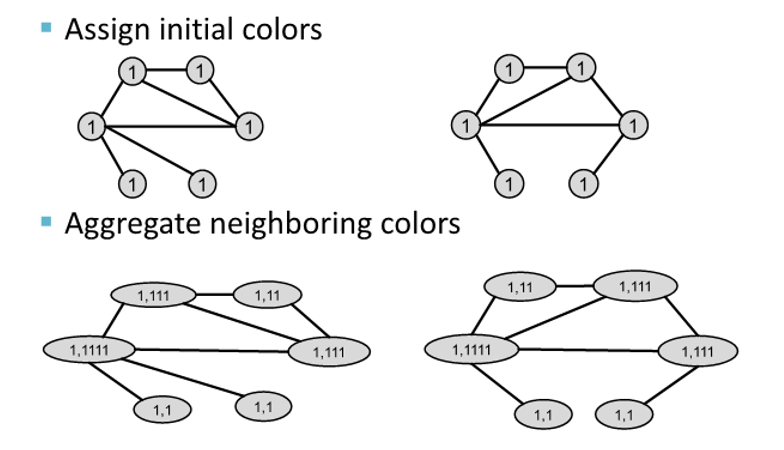
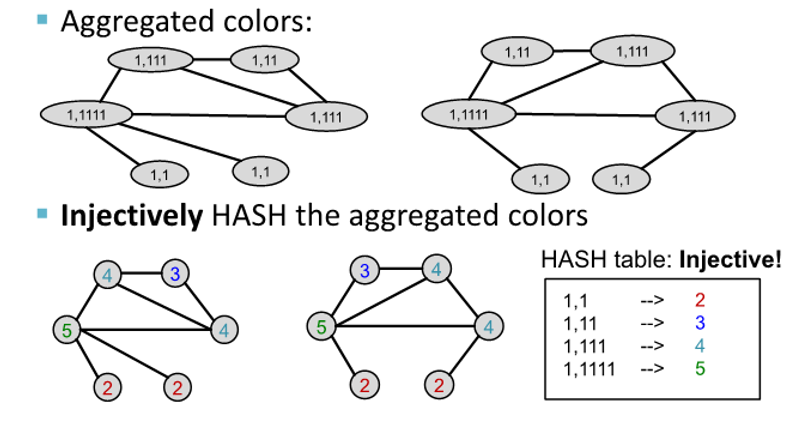
• stable coloring에 도달할 때까지 process가 이어짐
• 두 그래프가 같은 color set을 가진 경우, isomorphic하다고 함

GIN use Neural Network to model injective Hash Function

• $(1 + \epsilon)$
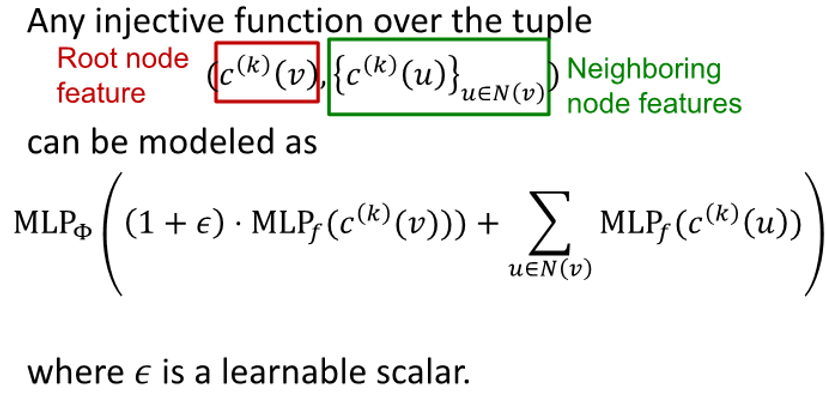
  : add one plus epsilon
• $MLP_{f}(c^{(k)}(v))$
  : our own message transformed by $k$
• $\sum\limits_{u\in\mathbb{N(v)}} MLP_f(c^{(k)}(u))$
  : take message from children and transform them using MLP, then sum up
• $MLP_{\Phi}($ $(1 + \epsilon)$ * $MLP_{f}(c^{(k)}(v))$ + $\sum\limits_{u\in\mathbb{N(v)}} MLP_f(c^{(k)}(u))$ $)$
  : add two together and pass through another function $\Phi$

input feature가 one-hot vector로 표현 가능한 경우, direct summation은 injective하기 때문에 $\Phi$가 injective하도록 보장하면 됨

GIN's node embedding update

• initial vector : $C^{(0)}(v)$ to each node
• interatively update node vector
  
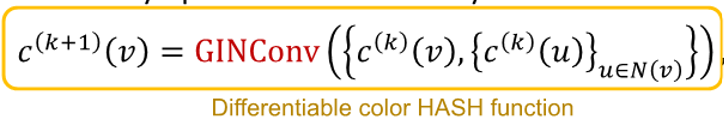
• after $K$ step of GIN iteration, $c^{(K)}(v)$는 $K$-hop neighborhood의 구조를 요약함

GIN and WL Kernel

GIN ~ differentiable neural network version of WL graph kernel
Advantage of GIN

• low dimensional of node embedding -> can capture fine-grained similarity of different node
• parameter of update function can be learned for the downstream task

GIN과 WL graph kernel의 연관성으로 인해 표현력은 동일
GIN은 실제 모든 graph를 구별 가능

Power of Pooling

Failure case of mean and max pooling
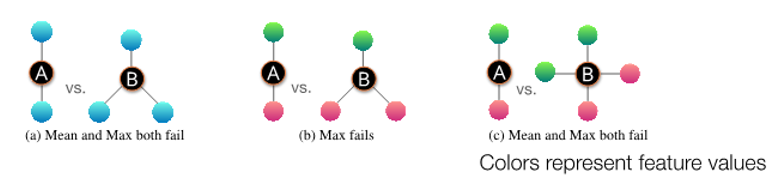(a) : type of neighborhood structure with all same feature
(b) : number of distinct color are same
(c) : proportion of distinct color is same

Ranking by discriminative power