작성자: 장예은

1. Machine Learning with Graphs (Intro)

• Types of Networks and Graphs
  그래프는 데이터를 독립적인 datapoint 보다는 entity 간의 관계로 보는 방법입니다. 다음은 그래프가 활용되는 다양한 사례입니다.
  
  
  

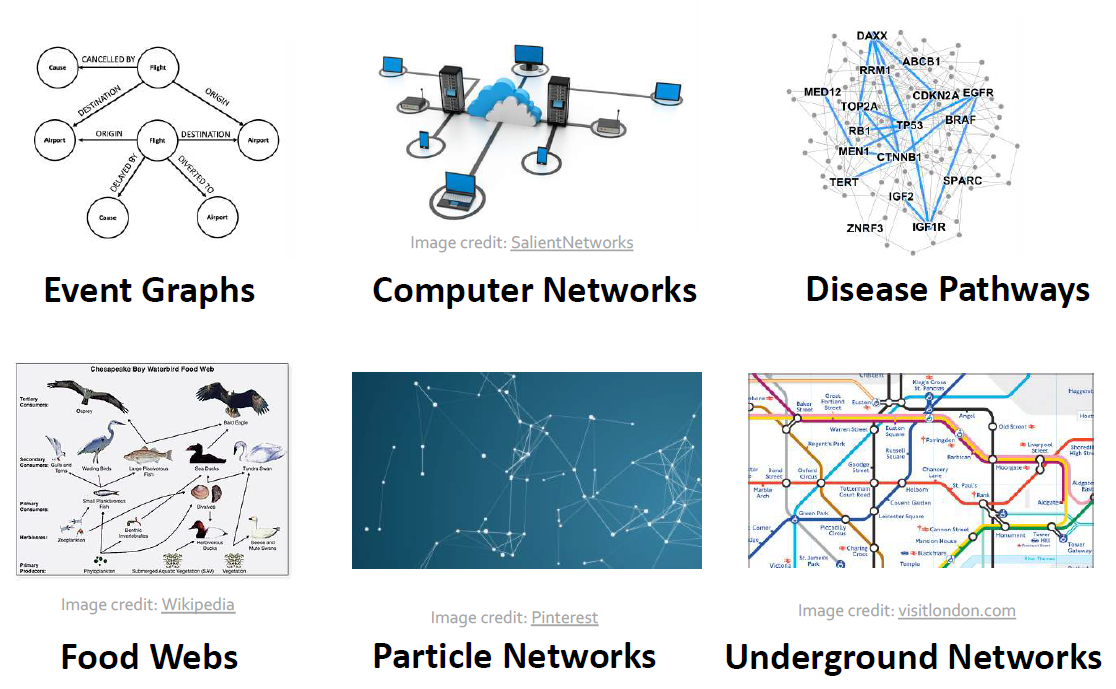
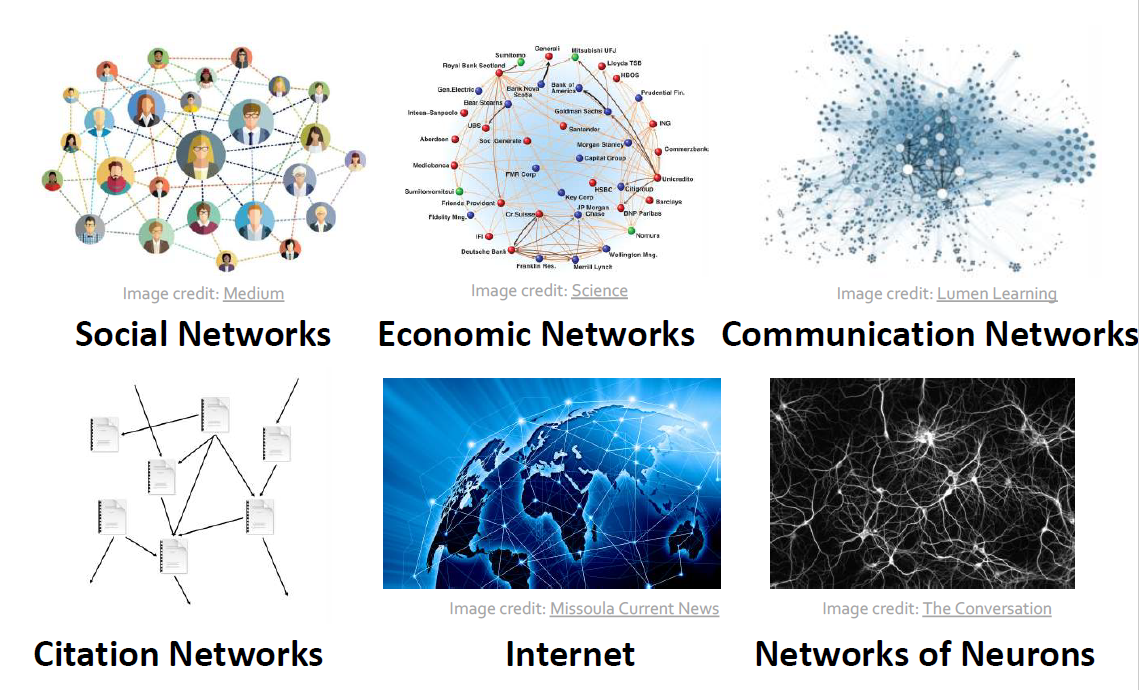
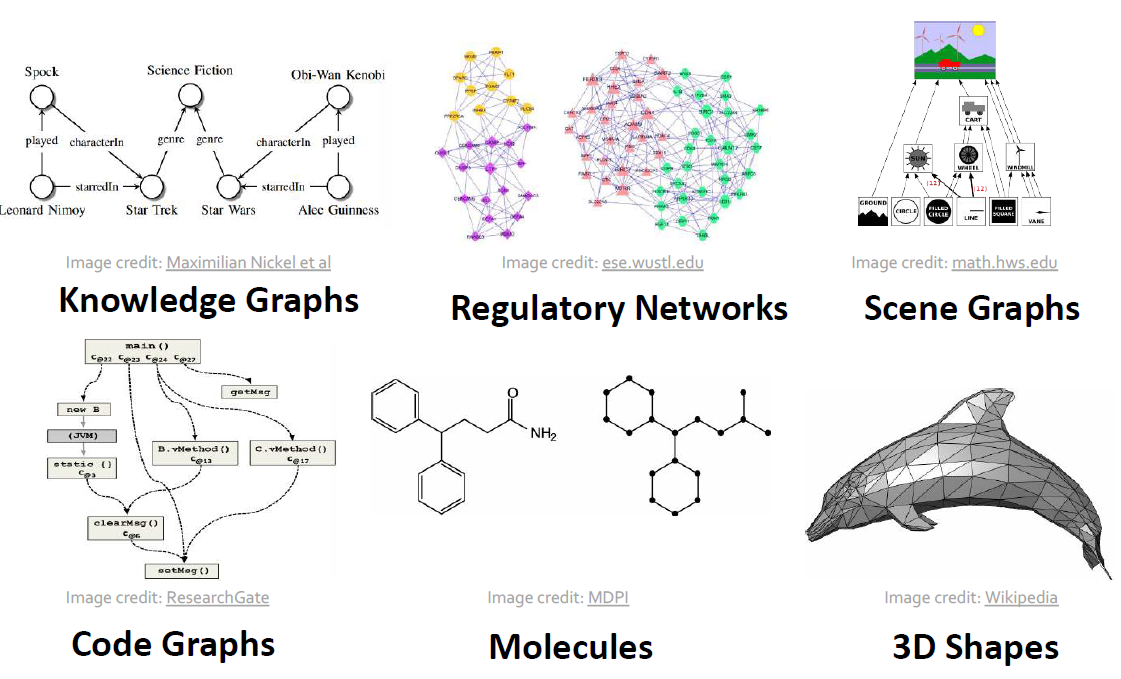
Networks (Natural Graphs)

Natural Graphs라고도 알려진 네트워크의 종류는 다음과 같습니다.

• Social Networks
• Communication and transactions : electronic devices, phone calls, financial transactions
• Biomedicine: interactions between genes/proteins
• Brain connections : connections between billions of Neurons

우리가 흔히 예상 가능한 소셜 네트워크나 커뮤니케이션, 거래 뿐만 아니라, Biomedicine과 뇌의 구조 조차도 네트워크에 해당합니다.

Graphs

그래프의 종류는 다음과 같습니다.

• Information / knowledge
• software
• similiarity networks : connections of similiar data points
• relational structures : Molecules, Scene graphs, 3D shapes, particle based physics simulations

지식과 정보 또한 링크 형태로 구조화되어있고, 소프트웨어, 유사성 네트워크, 관계 구조 등의 사례도 그래프로 표현이 가능합니다.

Networks와 Graphs의 경계가 모호한 경우도 많습니다. (실제로 본 강의자료에서도 두 용어를 혼용해서 사용하는 경우가 꽤 보입니다)

그래프 분석의 어려움

복잡한 도메인에서는 relational graph 로 표현 가능한 relational structure가 풍부합니다. 따라서 이러한 관계 데이터를 잘 이용하면 큰 가치를 이끌어낼 수 있습니다.
하지만 그래프는 다른 형태의 데이터에 비해 분석하기에 어려운 점이 많습니다.

기존의 이미지, 텍스트, 음성 데이터는 고정된 사이즈를 가지고 있고, 데이터의 사이즈가 일정하여 변하지 않습니다.

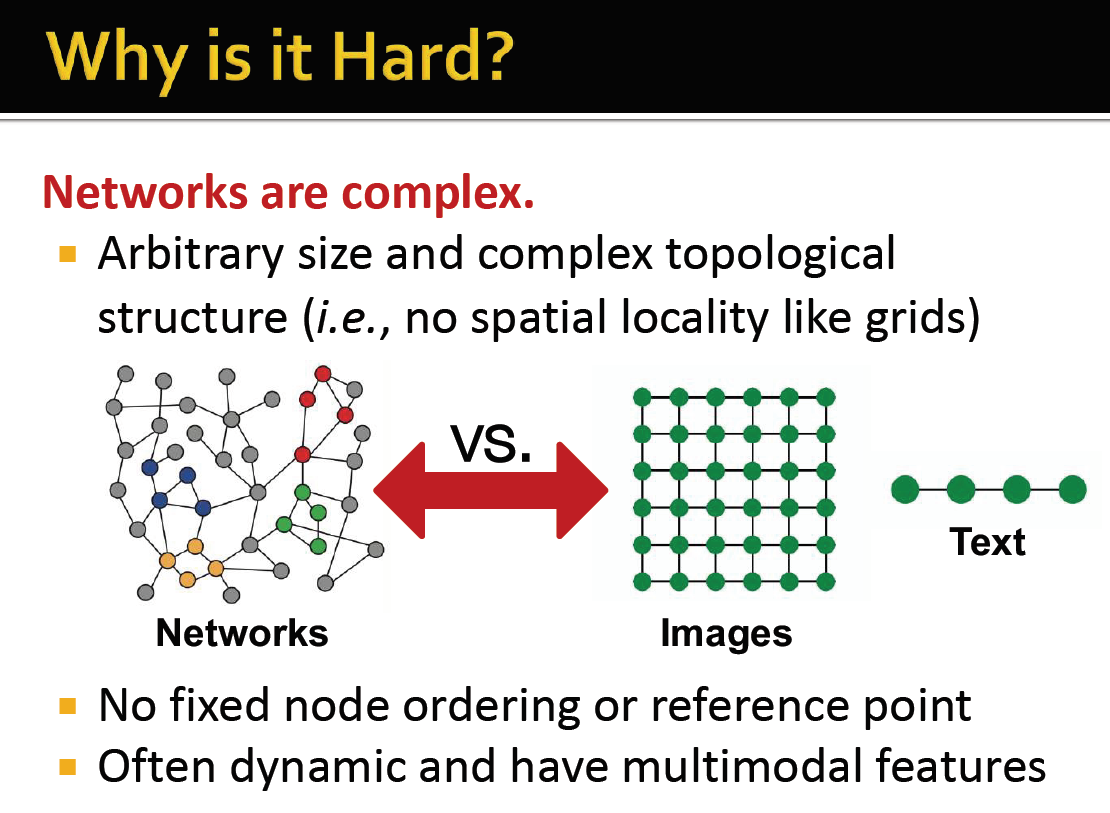
하지만 그래프는 사이즈가 임의적이고, 복잡한 위상학적 구조를 가지고 있습니다. Locality나 reference point가 따로 존재하는 것이 아니고, 때로는 dynamic하게 변화하거나 multimodal feature를 가지기도 합니다. 따라서 이러한 어려운 task를 어떻게 다룰지에 대한 아이디어가 다양하게 존재해왔고, 우리는 그것을 이 강의를 통해 배울 것입니다.

Representation Learning

전통적인 방법의 Supervised Learning은 매번 Feature engineering을 통해 성능을 개선합니다.
하지만, Representation Learning은 그래프의 feature를 자동으로 학습하게 만들어 feature engineering이 필요하지 않게 합니다.

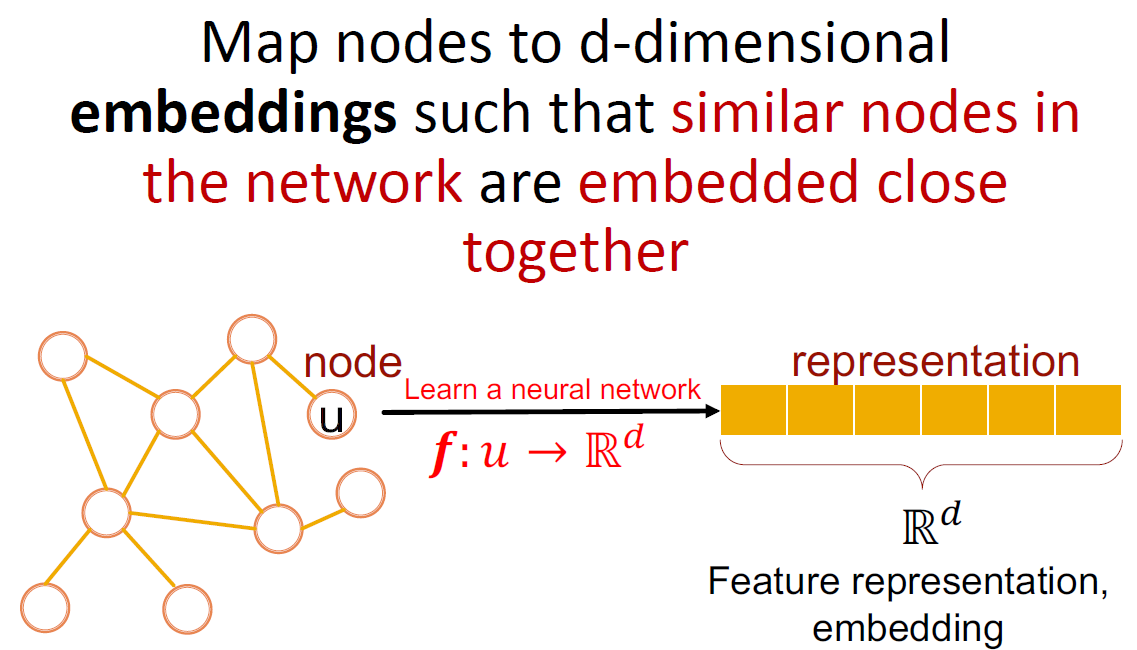
Representation Learning은 유사한 노드끼리 임베딩 공간에서 가깝도록 d차원으로 노드를 임베딩하는 것입니다.

CS224W 전체 개요

CS224W 강의의 전체적인 내용 흐름은 다음과 같습니다.

2. Applications of Graph ML

2.1. Classic Graph ML Tasks

Task는 다음과 같이 Node level, Graph level prediction, Graph generation, Subgraph level, Edge level 등으로 구분될 수 있습니다.

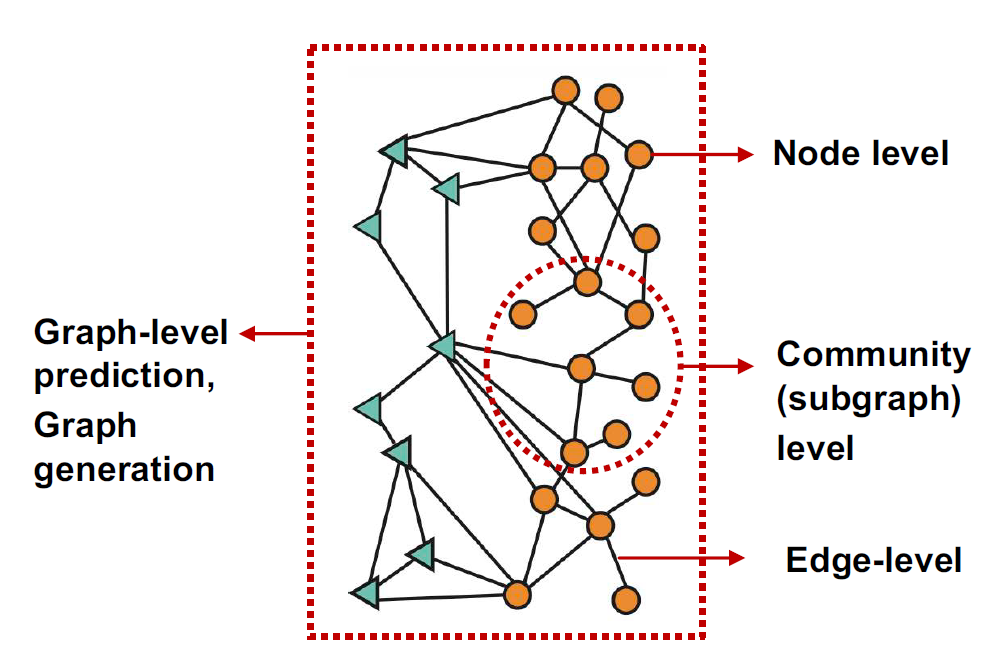
기본적인 그래프 머신러닝 Task는 다음과 같습니다.

• Node classification : Node의 property를 예측한다 (ex- 온라인 user와 item을 카테고리화 한다)
• Link prediction : 두 Node사이에 missing link를 예측한다
• Graph classification : 그래프를 카테고리화 한다 (ex - 분자의 property를 예측한다) => 신약 개발에 도움
• Clustering : Node가 클러스터를 구성하는지 탐지한다. (Social circle detection)
• Graph generation : 신약개발 (drug discovery)
• Graph evolution : 물리학 실험

2.2. Examples of Node-level ML Tasks

Protein Folding Problem (단백질 접힘 문제)

출처 위키피디아

단백질의 구조는 아미노산 서열의 선형 복합체이지만, 대부분 접힌 형태로 존재한다고 합니다. 단백질의 고유한 접힌 형태는 아미노산 서열 정보에 의해 결정됩니다.

하지만, 어떠한 아미노산 서열 조합이 어떤 접힘 구조를 야기하는지 결과를 예측하기는 쉽지 않고, 어려운 문제로 손꼽히고 있습니다.

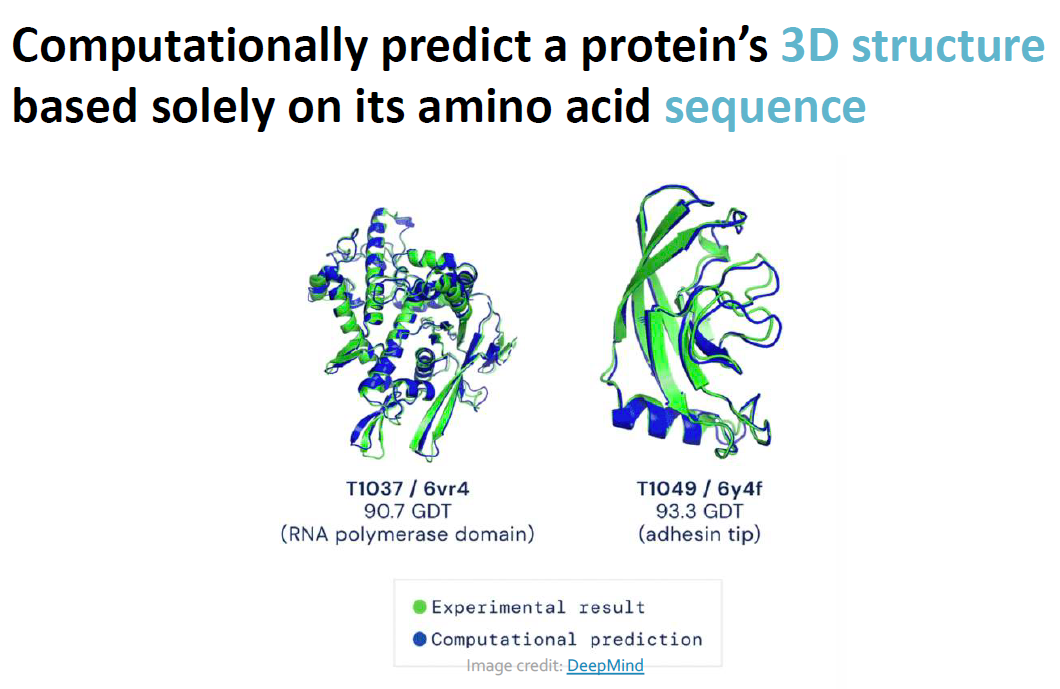
그래프 모델은 아미노산 서열만을 이용하여 다음과 같은 방법으로 단백질의 접힘 구조를 예측합니다.

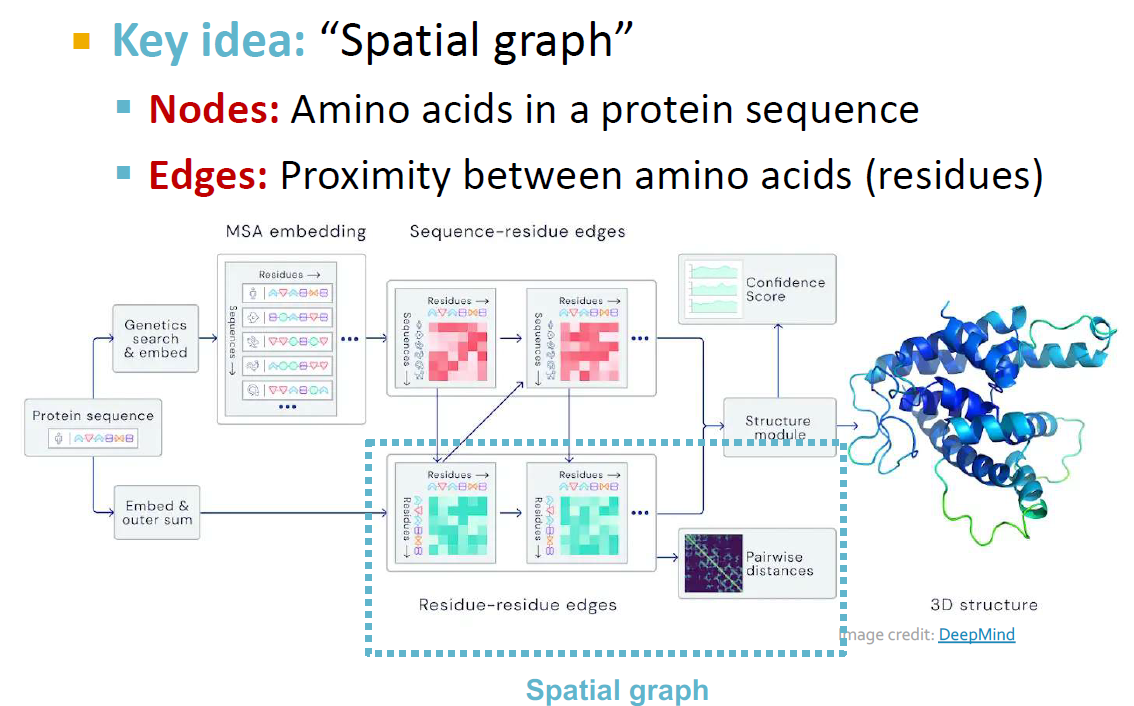
아미노산의 서열은 Node에 대응되고, 아미노산 간의 근접성은 edge에 대응됩니다. Node, edge 정보와 그래프의 구조를 통해 단백질의 새로운 위치를 예측하는 것입니다. 이후의 강의에서 더 자세히 배울 것이니 여기서는 GNN을 통해 화학 분야에서의 어려운 문제를 해결했다는 점만 알아두셔도 좋습니다.

2.3. Examples of Edge-level ML Tasks

edge를 예측

Recommendation systems

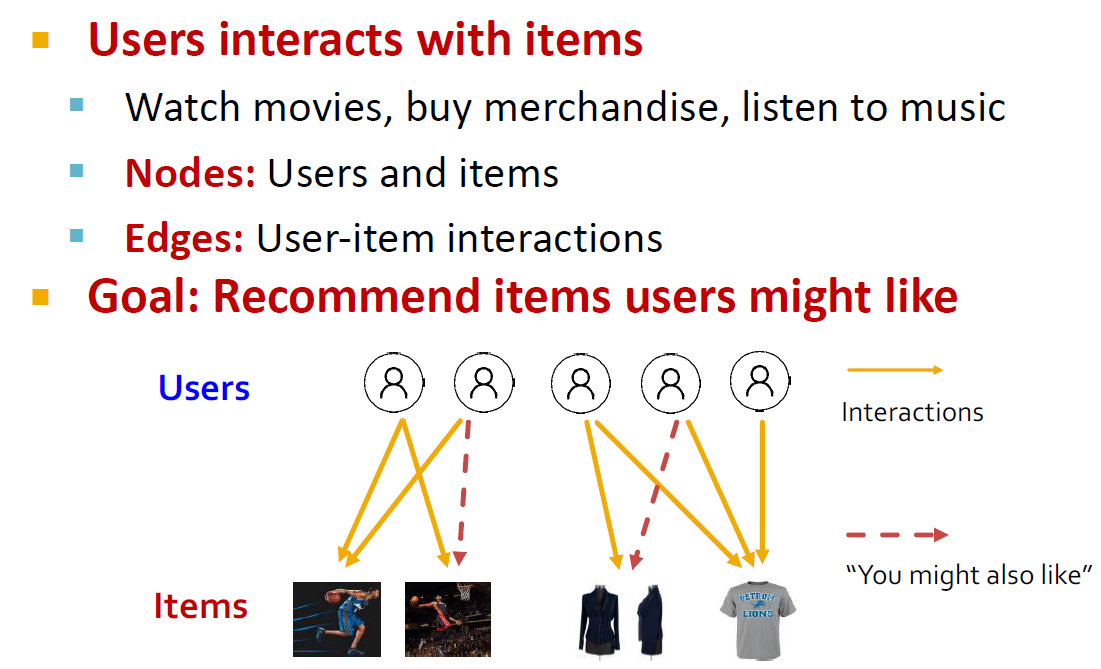
추천시스템도 GNN이 성공적으로 사용되고 있는 분야 중 하나입니다. 노드는 user또는 item에 해당하고, 엣지는 user-item interaction에 해당합니다. 여기서 user-item interaction은 user가 item을 구매했는지 / 클릭했는지 등의 상호작용을 의미합니다. 만약 유저가 해당 아이템을 구매했다면, 해당 유저와 아이템 사이에는 링크가 존재하는 구조입니다. 유저가 구매하지 않은 아이템 중에서 유저가 선호할만한 아이템을 추천해주는 것이 추천 시스템인데요, 이것을 그래프 구조에서 해석하면 링크가 존재할 법 하지만 링크가 없는 유저와 아이템 사이의 링크를 예측하는 것이 됩니다.

Drug Side Effects

많은 환자들은 여러 가지의 질환을 치료하기 위해 여러 종류의 약을 동시에 복용합니다. 그렇기 때문에 서로 다른 약의 조합이 일으키는 부작용을 예측하는 것이 중요합니다.

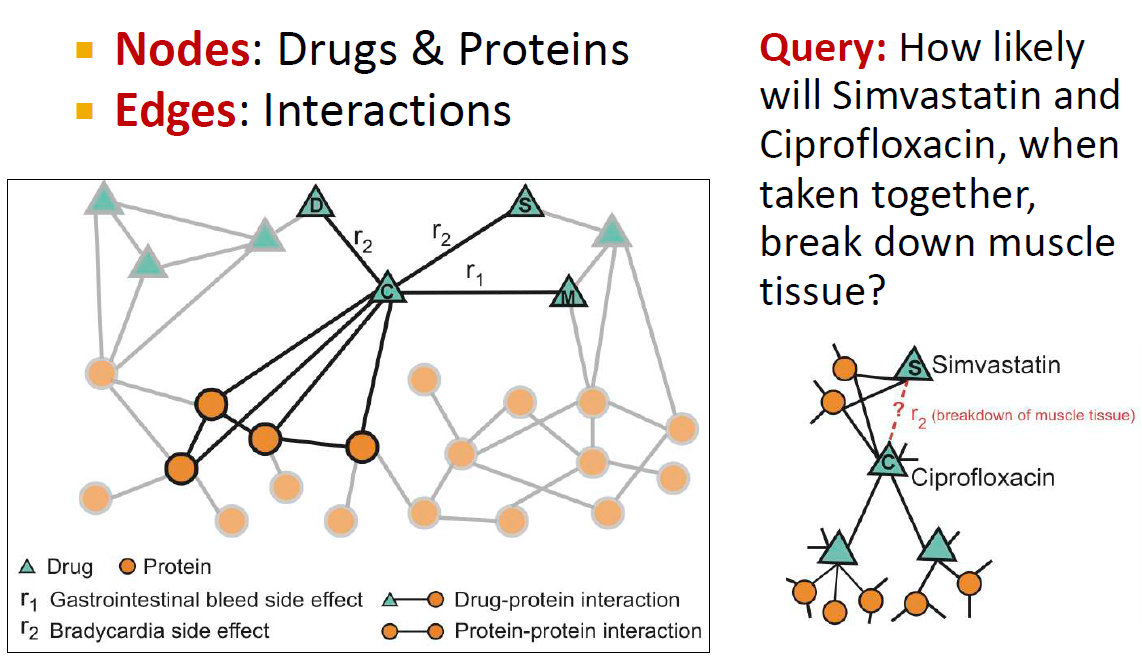
좀 더 구체적으로는, 약과 단백질이 node에 해당하고, 서로간의 interaction이 edge에 해당합니다. 그래프를 통해 edge에 해당하는 interaction을 예측합니다.

2.4. Examples of Subgraph-level ML Tasks

subgraph 단위로 예측에 사용

Traffic prediction

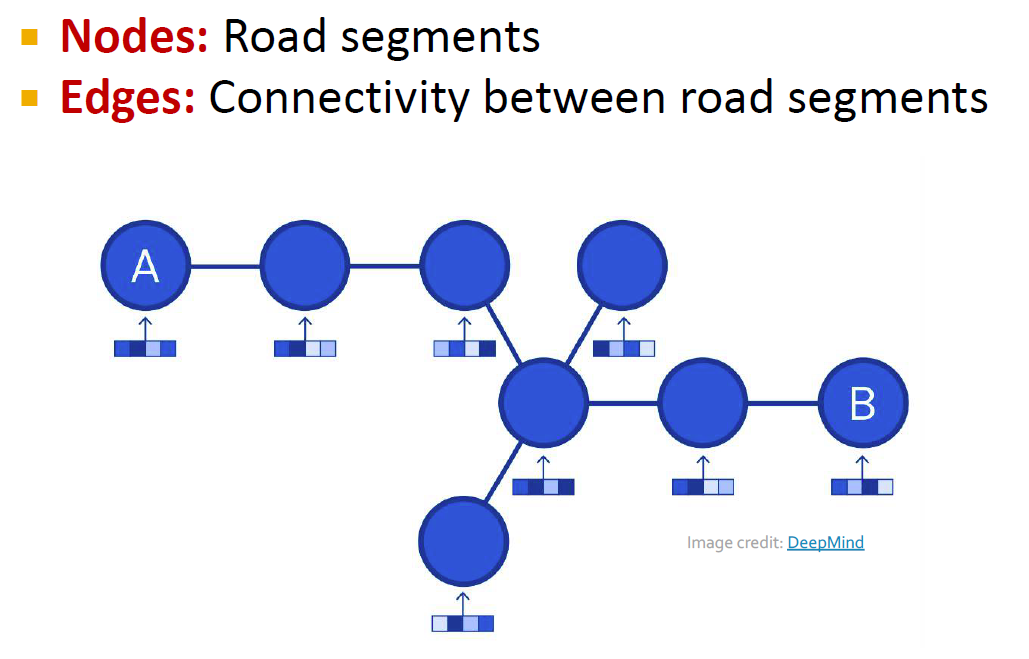
우리가 자주 사용하는 지도 앱의 길찾기 기능도 그래프 ML의 예측 결과입니다. Node는 도로 구간에 해당하고, edge는 도로 구간들의 연결성을 나타냅니다. 그래프 ML이 우리가 검색하는 경로가 걸리는 시간을 예측합니다.

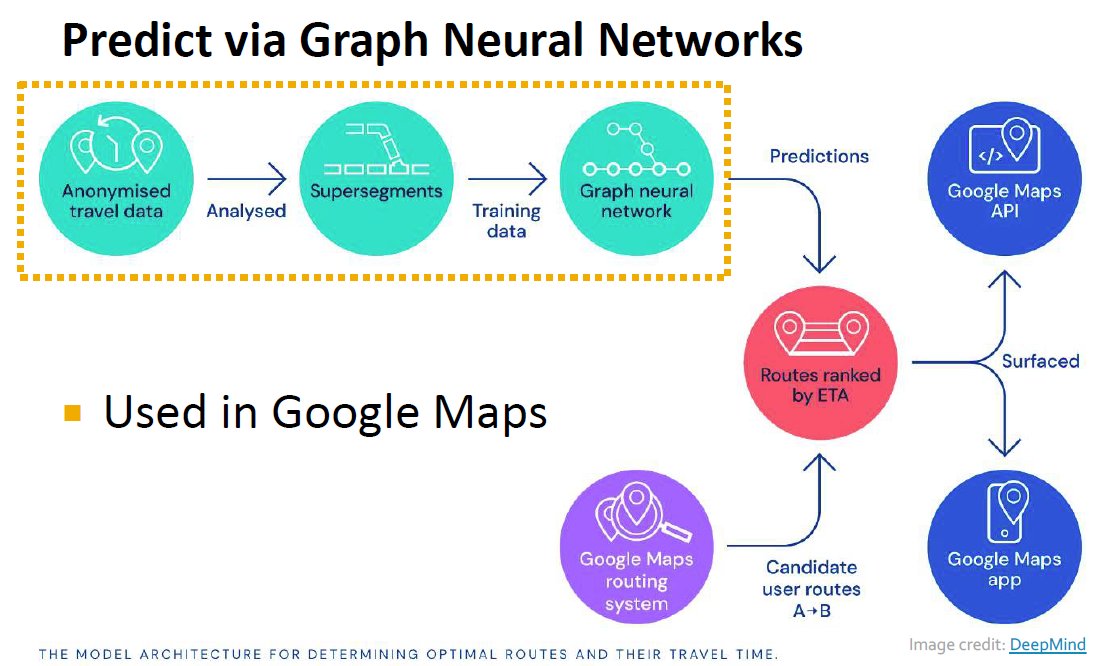
이러한 과정을 통해 구글맵과 같은 지도는 우리가 요청한 경로에 소요되는 시간 (ETA)를 계산하고, 가장 시간이 적게 걸리는 경로를 추천해주는 것입니다.

2.5. Examples of Graph-level ML Tasks

Graph level prediction, Graph generation

Drug Discovery

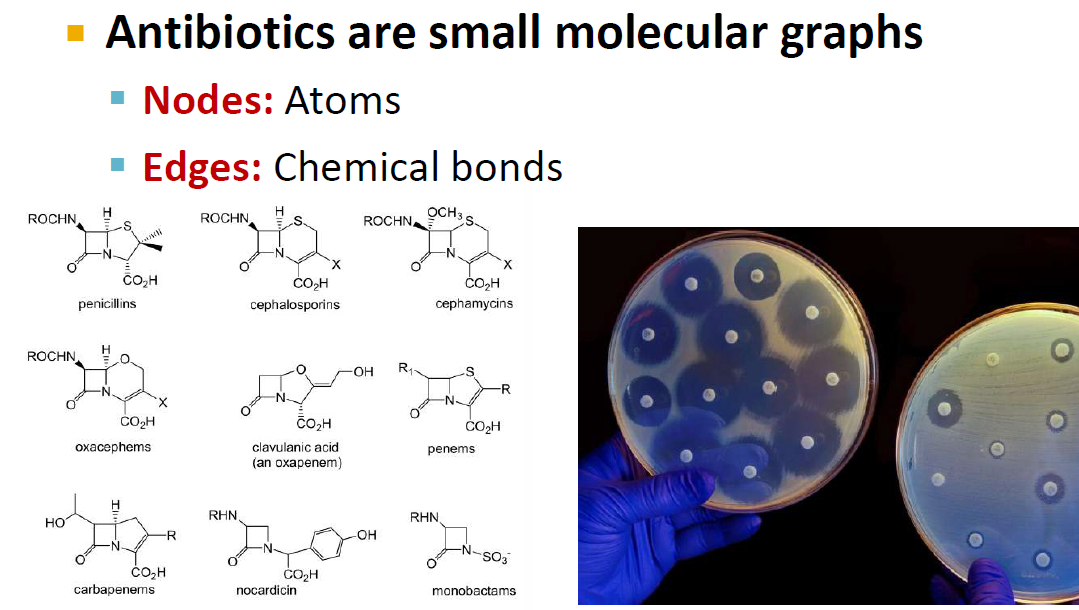
항생제의 구조는 작은 분자 그래프입니다. 이 그래프에서 Node는 원자에 해당하고, edge는 화학적 결합에 해당합니다. 원자는 수백만개가 존재하기 때문에 어떤게 치료 효과를 나타낼 지 알 수 없습니다. 따라서 그래프를 이용하여 atom candidates pool에서 적합한 원자를 고르는 방식으로 새로운 약 구조를 찾습니다. 이것은 node를 classify 하기 때문에 Graph classification model에 해당합니다.

Molecule Generation / Optimization

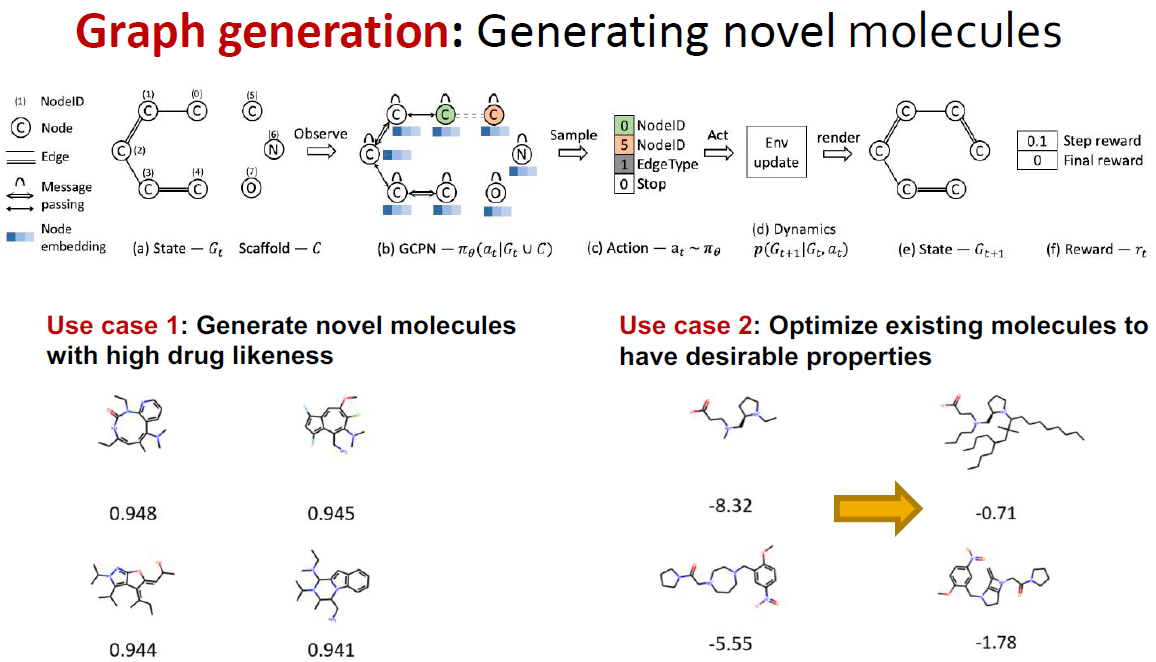
Molecule Generation은 원하는 특성을 가진 새로운 분자를 만들어내는 것을 목표로 합니다. GNN을 통해 'high drug likeness'하거나 non-toxic 등의 원하는 특성을 가지는 새로운 분자를 합성시키는 것입니다. (Drug discovery와 유사)

Physics Simulation

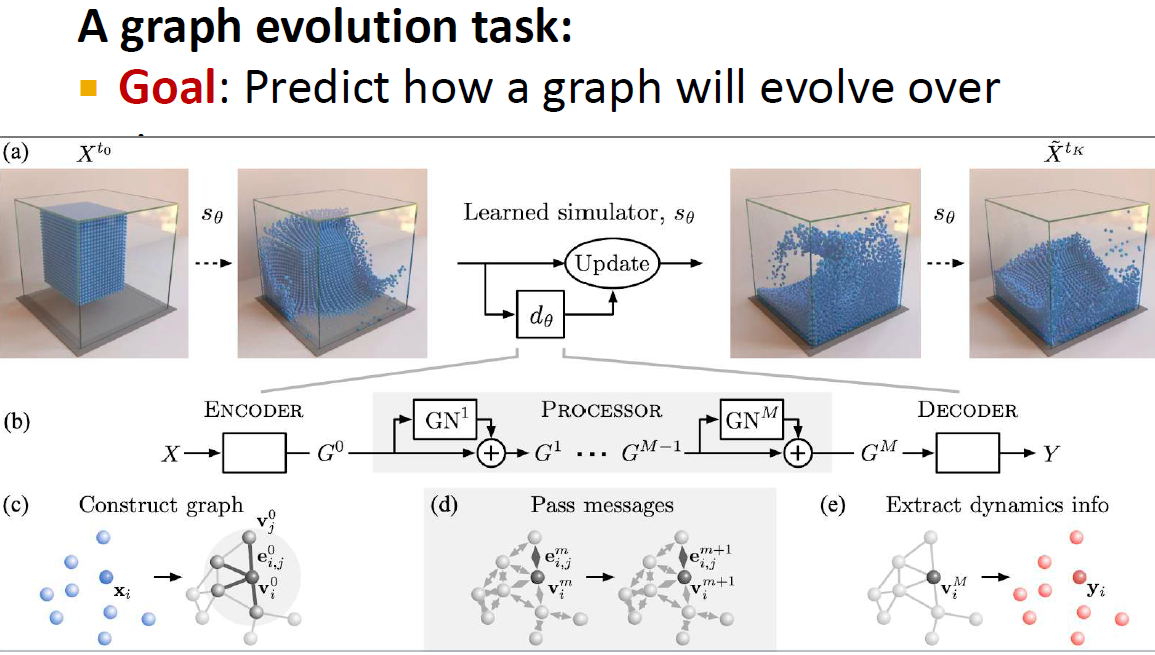
GNN은 물리학 시뮬레이션에도 사용됩니다. Node는 입자에 해당하고, edge는 입자 간의 interaction에 해당합니다. 좀 더 상세하게 살펴보면, 먼저 (c) 입자 간의 proximity 기반으로 proximity graph를 생성하고, GNN을 적용하여 (d) 입자의 미래 위치와 속도를 예측합니다. 이후 (e) 예측을 바탕으로 입자를 새 위치로 변경한 후, proximity graph를 새로 구축하고, 이 과정을 반복합니다. 이것을 통해 이 물질이 어떻게 'deform'하는지 알 수 있다고 합니다.

3. Choice of Graph Representation

3.1. Components of a Network

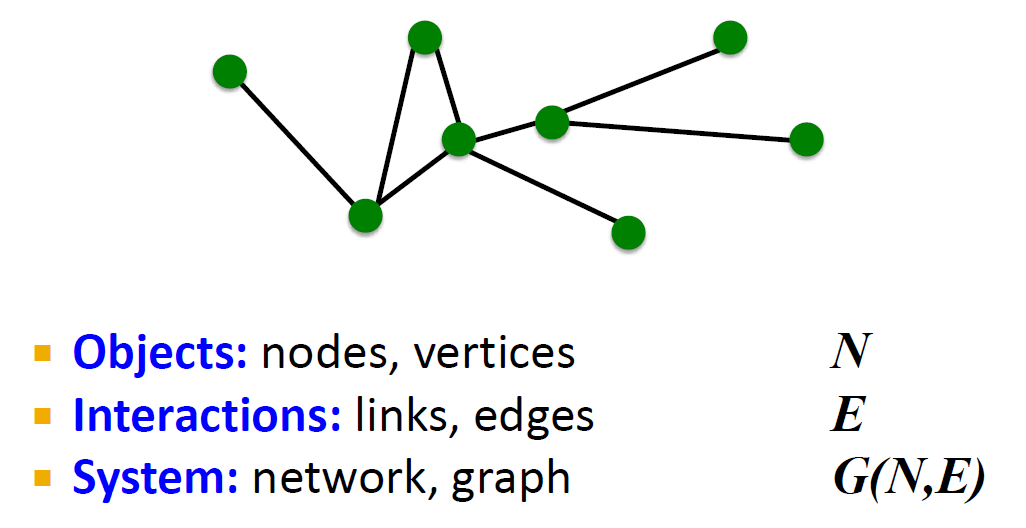
네트워크의 Objects는 node, vertice를 의미하며 N으로 표기합니다. Interactions는 link, edge를 의미하고, E로 표기합니다. System은 network와 graph에 해당하며, G(N,E)로 표기합니다.

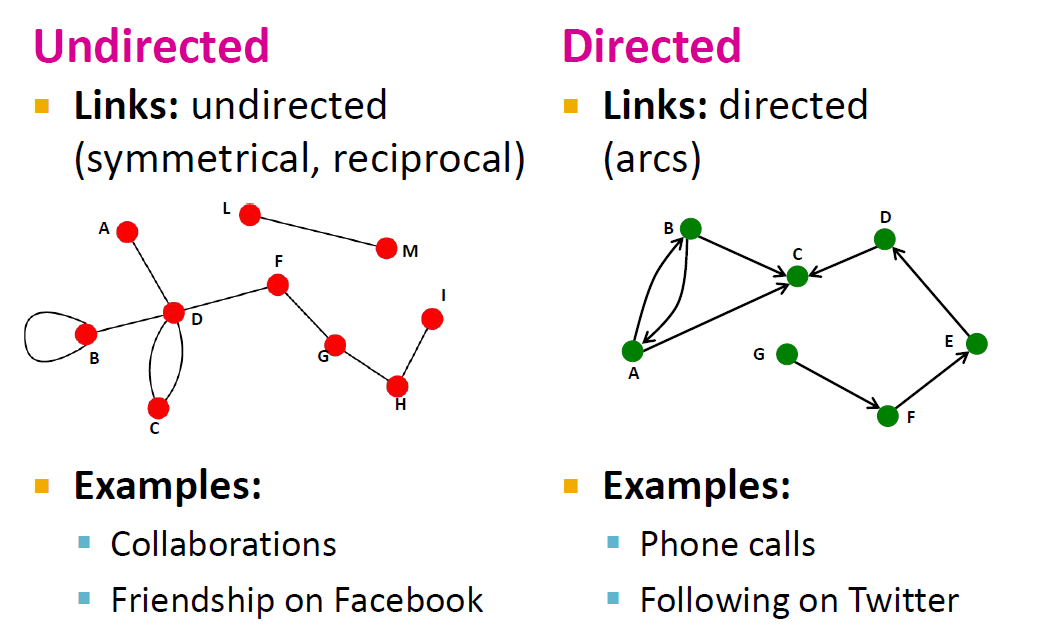
그래프는 edge의 방향성이 없는 경우에 Undirected, 있는 경우에 Directed으로 구분됩니다. Undirected 그래프로 표현될 수 있는 사례는 협업, 페이스북 친구 등이 있습니다. 어떤 방향성이 있다기보다는 서로간의 관계를 나타내는 구조이기 때문입니다.

Directed graph는 source와 destination이 구분되어 있는 구조로, 표현될 수 있는 사례로는 통화, 트위터 팔로우 등이 있습니다. 이 경우에는 전화를 건 사람과 받는 사람, 팔로우를 한 사람과 팔로우를 당한 사람이 구분되어 있기 때문에 directed 구조가 더 적합합니다.

Node degree

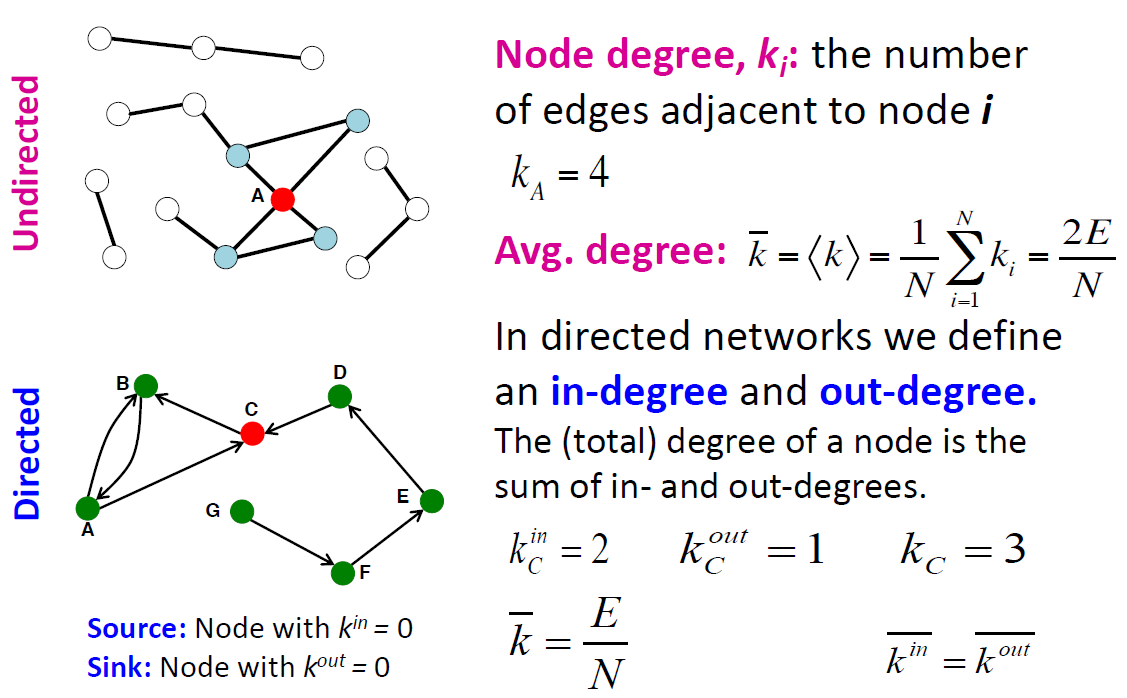
Node degree는 directed graph와 undirected graph가 각각 계산 방식이 다릅니다. Undirected graph에서 node degree는 노드 i에 인접한 엣지의 개수입니다. 평균 degree는 $2E/N$ (E: 엣지 수, N: 노드 수) 인데 모든 엣지가 2번씩 세어지기 때문입니다.

Directed graph에서의 node degree는 in-degree와 out-degree로 나뉩니다. 노드 c의 총 degree는 in과 out degree를 모두 합친 값입니다.

지금까지는 비교적 단순한 node와 edge attributes를 다루었지만, 다음과 같은 대상들 또한 그래프의 node와 edge로 표현될 수 있습니다.

More types of Graphs

how do you define a graph?

많은 종류의 그래프가 존재하는 만큼, 우리의 task에 맞는 그래프를 선택하는 것이 중요합니다. 적절하게 그래프를 구성하려면 노드와 엣지가 될 요소를 적절하게 선정해야 합니다.

Bipartite Graph

Bipartite graph에서는 두가지의 다른 노드 종류(U,V)가 존재하고, 엣지는 항상 한 종류에서 다른 종류로만 연결될 수 있습니다(U와 V끼리만 링크 가능, U끼리/V끼리 불가능)
이러한 형태의 그래프는 앞서 언급했던 추천시스템에서 user와 item을 모델링하는 데에 적합합니다. 뿐만 아니라, 논문과 저자, 배우와 출연한 영화, 레시피와 재료 등의 경우를 모델링하는데에도 아주 유용합니다.

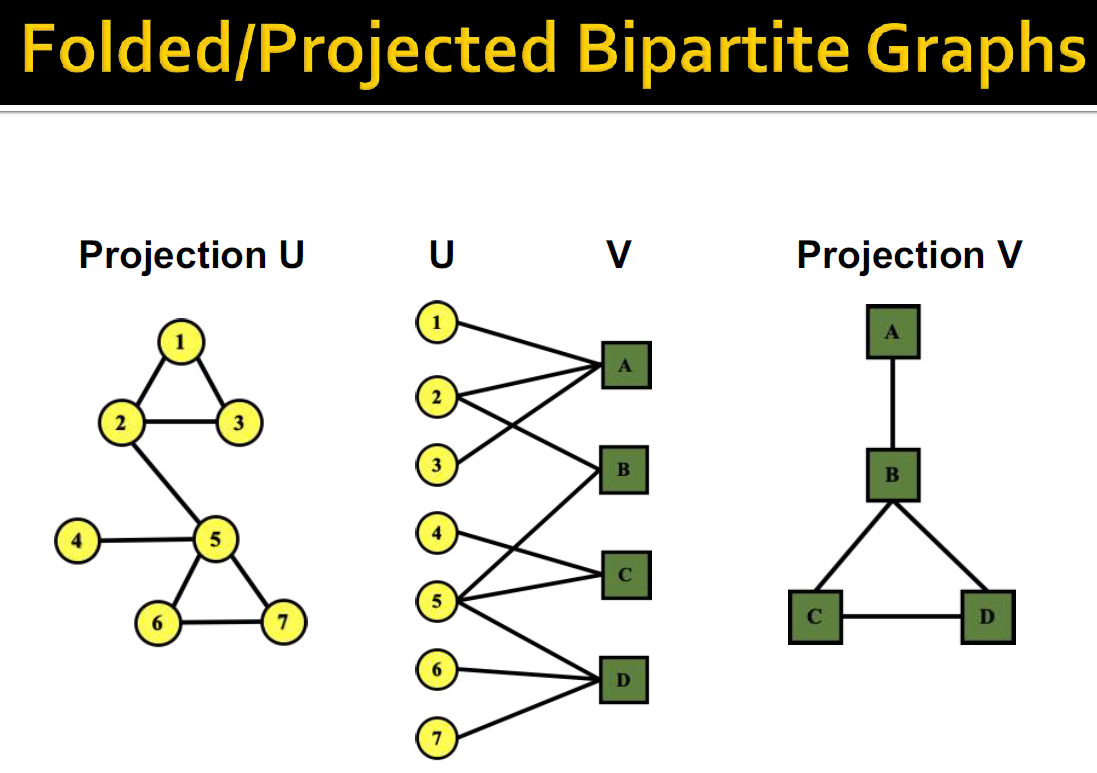
Folded Bipartite networks(graphs)는 Projected Bipartite networks(graphs) 라고도 불립니다. 이 그래프는 Bipartite graphs에서 같은 종류의 노드 내에서의 연결성을 의미합니다. 왼쪽의 Projection U는 저자들끼리 공동작업한 논문이 있는 경우에 저자 간에 link가 존재하고, 오른쪽의 projection V에서는 논문 간에 공동 저자가 존재하면 link가 존재합니다.

3.2. Adjacency Matrix (인접행렬)

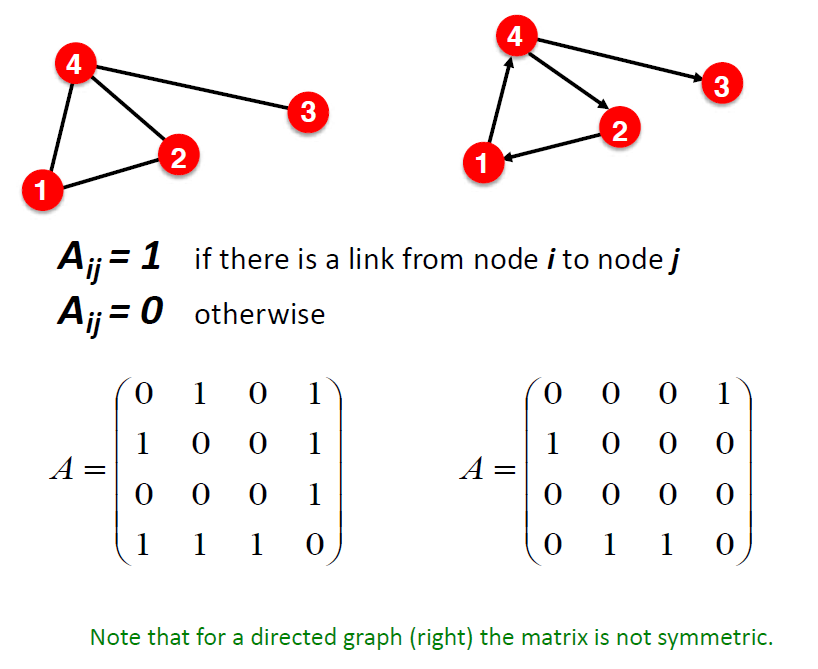
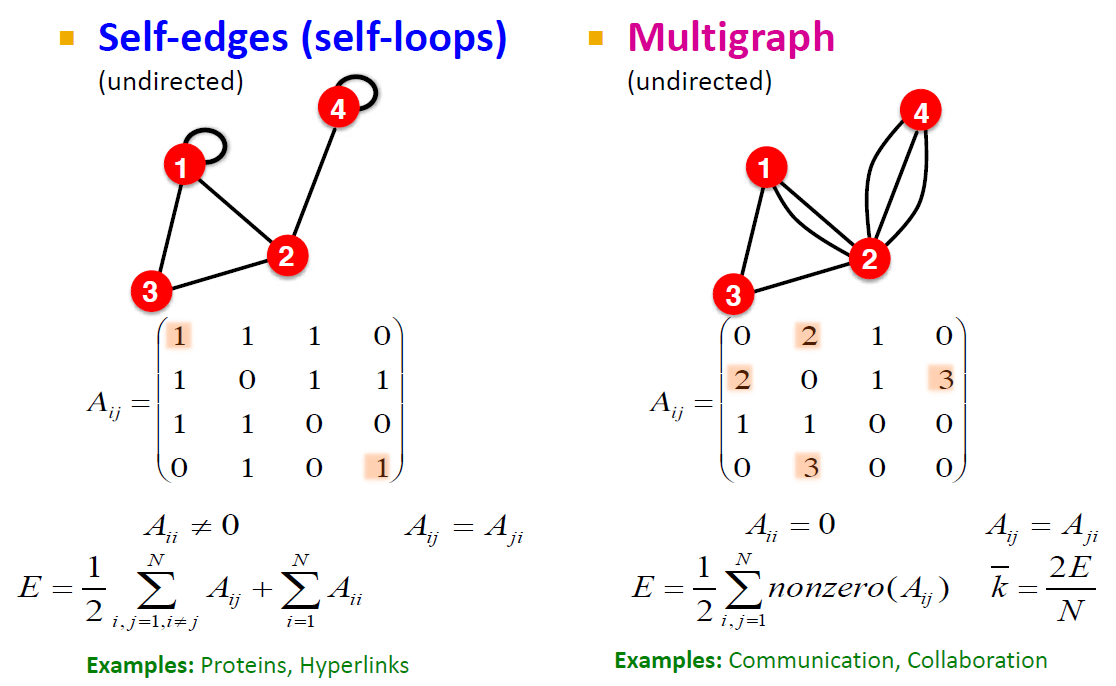
인접행렬은 그래프를 행렬 형태로 나타낸 것입니다. 노드 i에서 j 사이에 링크가 존재할 경우 1, 존재하지 않을 경우 0으로 표현합니다. 행과 열은 각각의 노드를 의미합니다. Undirected graph의 인접행렬은 왼쪽과 같이 대칭 형태이고, directed graph의 인접행렬은 오른쪽과 같이 비대칭 형태입니다.

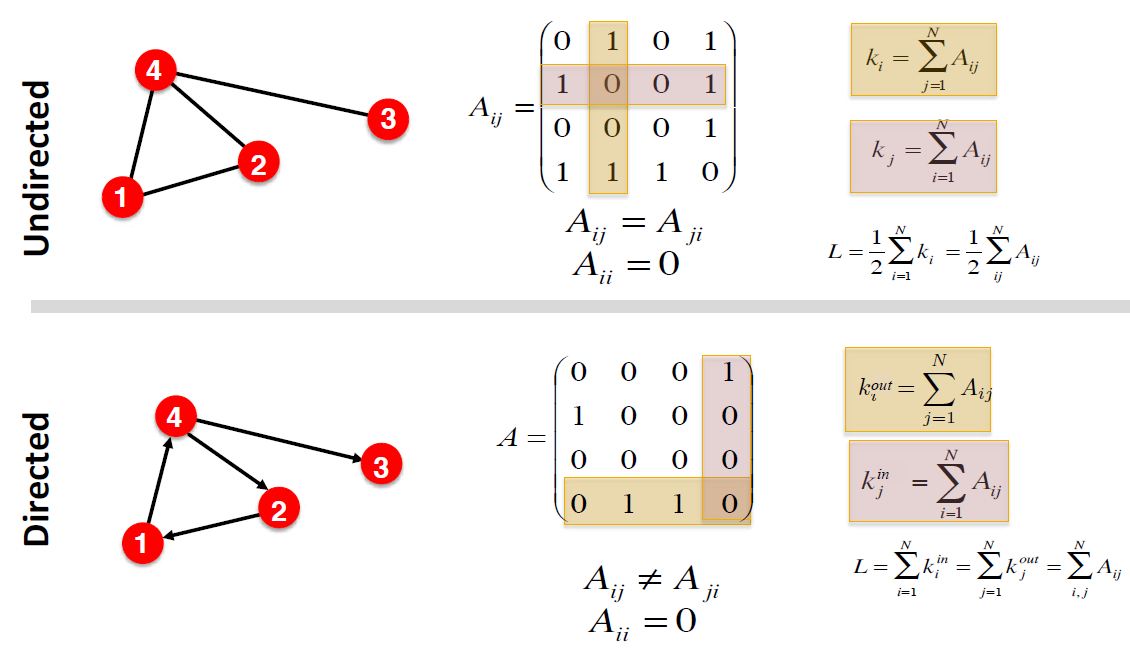
인접행렬에서는 node degree를 단순 행과 열의 합으로 구할 수 있습니다.

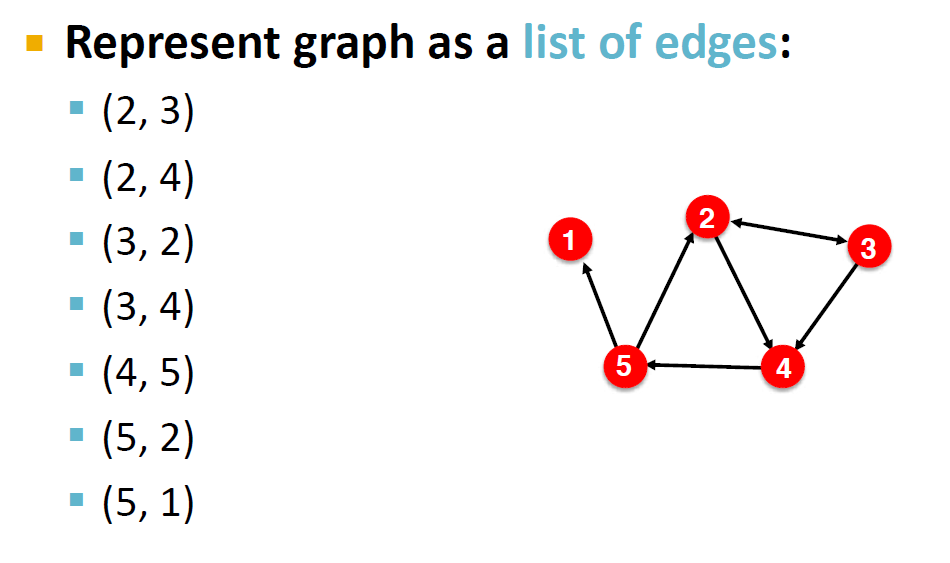
인접행렬은 대부분 Sparse하다는 문제점을 가지고 있습니다. 이 경우에서 인접행렬의 단점을 해결하기 위해 list of edge를 사용합니다. 이 방법은 특정 노드와 연결된 neighbor nodes를 쉽게 알 수 있다는 장점도 가지고 있습니다.

3.3. Connectivity

connectivity of undirected graphs

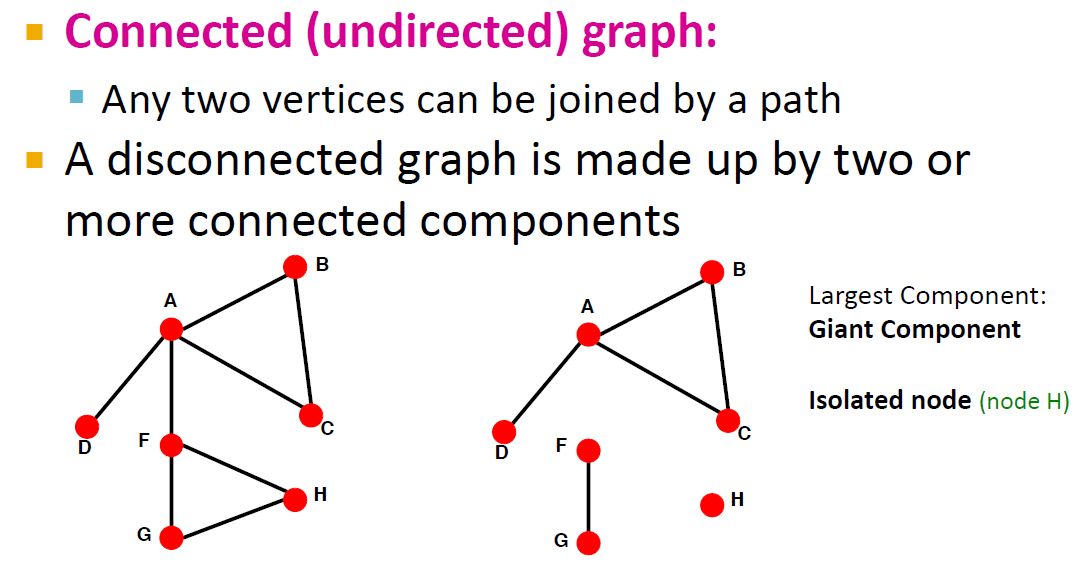
undirected graph에서의 연결성은 임의의 두 노드(vertices, nodes)가 경로로 연결될 수 있는지를 의미합니다. 왼쪽 그림은 임의의 두 노드가 모두 경로로 연결될수 있기 떄문에 연결성이 존재하는(connected) 경우입니다. 오른쪽 그림은 F, G에서 A~D로 갈 수 있는 경로가 존재하지 않고, H도 마찬가지입니다. 이 그래프는 A-D ,F-G끼리 연결되어있지만 그래프 전체로는 연결되어있지 않습니다(disconnected).

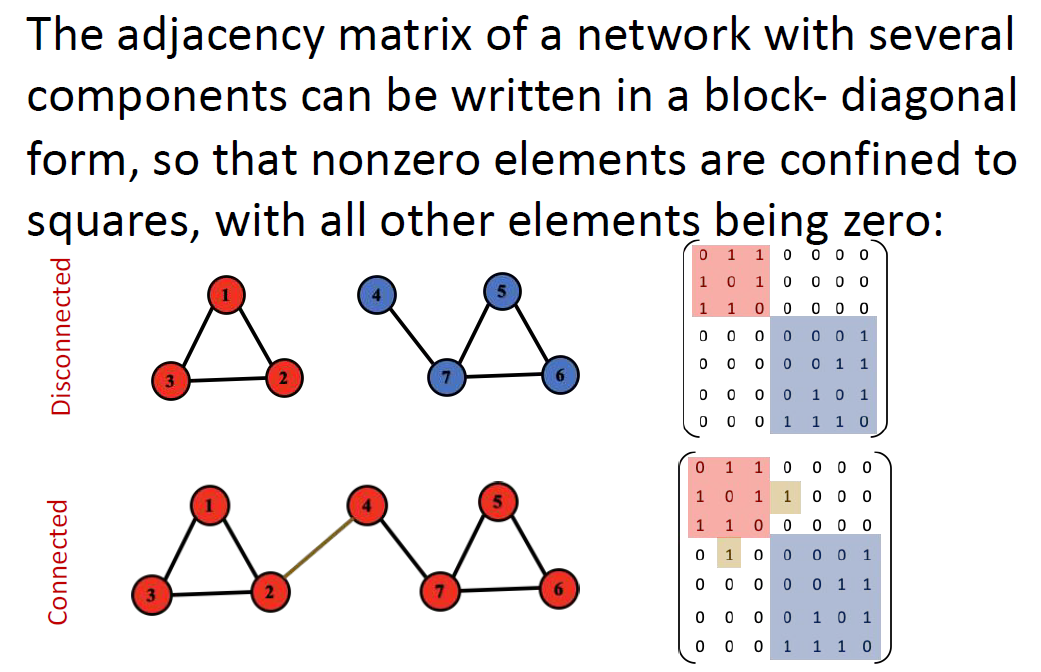
인접행렬을 통해 보면 이러한 차이를 보입니다.

Connectivity of Directed graphs

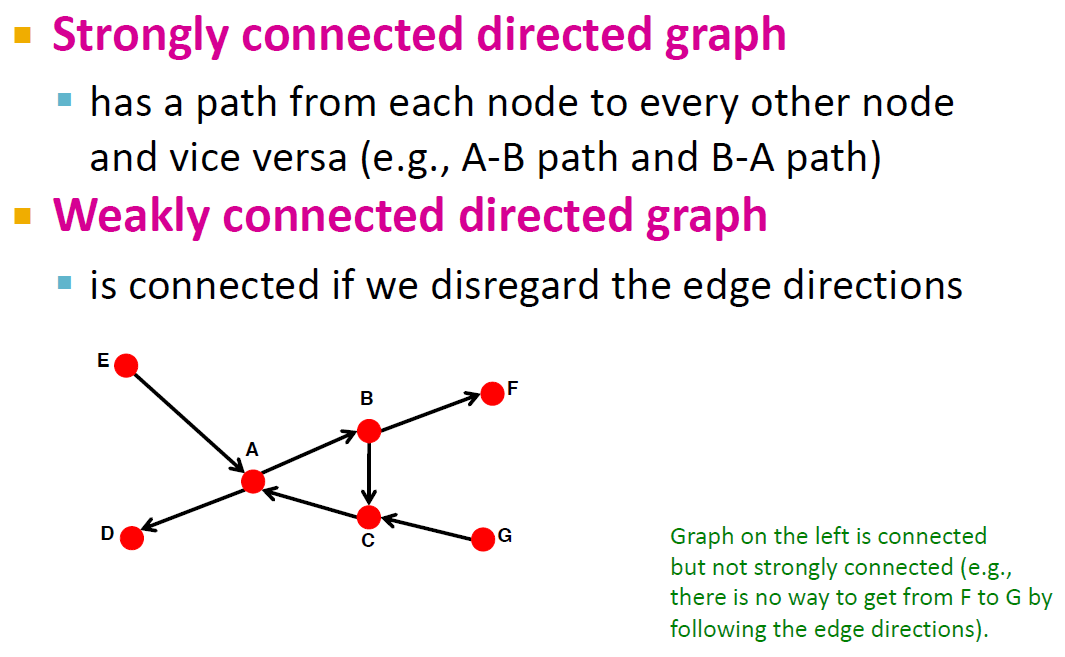
Directed graph에서의 연결성은 strongly connected와 weakly connected로 나뉩니다. 전자는 임의의 두 노드에서 모든 방향으로의 경로가 존재하는 경우이고(A와 B 사이에 A->B, B->A 모두 가능), 후자는 적어도 한 방향으로의 경로가 존재하는 경우입니다.

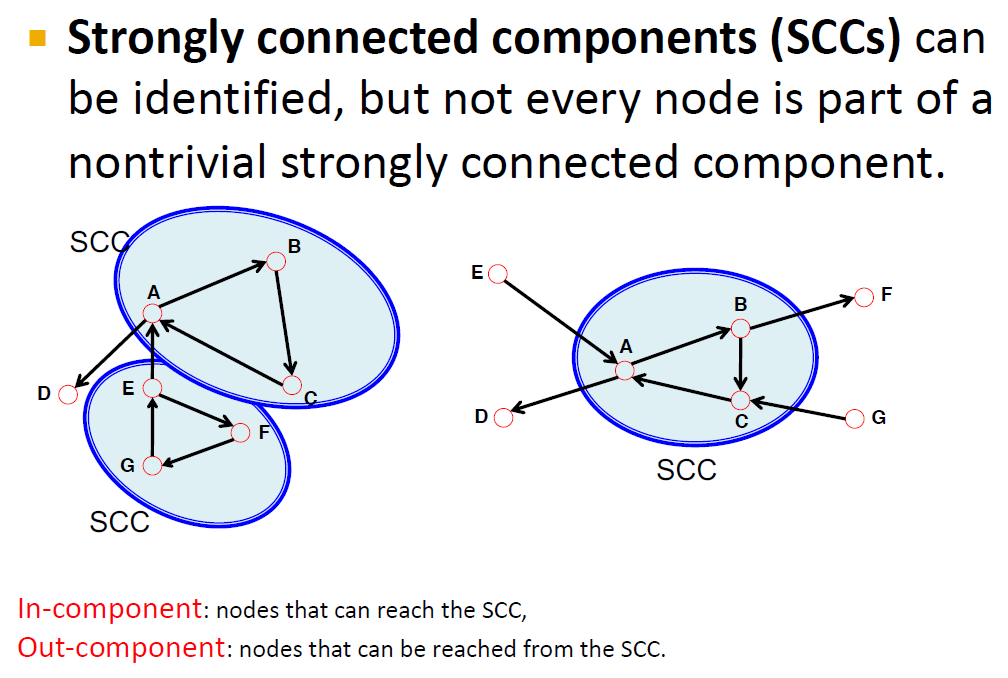
Strongly connected component는 directed graph에서 이렇게 cycle을 이루는 노드 조합을 의미합니다.