작성자: 이성범

0.Intro

본 장에서는 Node, Link, Graph를 feature로 만드는 방법에 대하여 다룬다. 아래와 같은 Machine Learning Tasks를 수행하기 위해서는 Node, Link, Graph를 feature로 만드는 것이 중요하다.
(본 장에서는 hand-designed features와 undirected graphs를 다룬다.)

• Machine Learning Tasks in Graphs

  • Node-level prediction
  • Link-level prediction
  • Graph-level prediction

• Machine Learning in Graphs

  • Goal : Make predictions for a set of objects
  • Design choices
    - Features : d-dimensional vectors
    - Objects : Nodes, edges(links), sets of nodes, entire graphs
    - Objects function : 우리의 task를 해결하는 함수
    

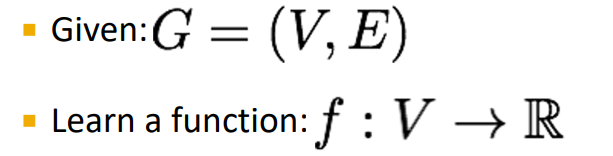
1.Node-level Features

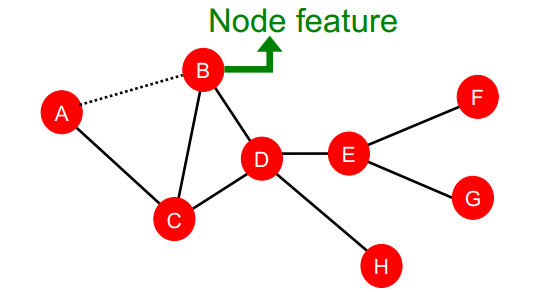
• Node의 feature를 구하는 방법
  • Node degree
  • Node centrality
  • Clustering coefficient
  • Graphlet Degree Vector

1-1 Node degree

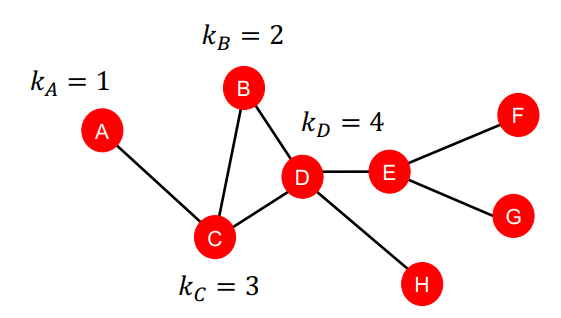
• 모든 근접 노드를 동등하게 바라봄
• 노드와 연결된 엣지의 개수를 사용

1-2 Node centrality

Node degree는 Node의 중요도를 반영하지 않기 때문에 노드의 중요도를 반영하기 위해서는 Node centrality를 사용해야 한다.

• Node centrality 구하는 다양한 방법
  • Engienvector centrality
  • Betweenness centrality
  • Closeness centrality
  • and many others…

(1) Engienvector centrality - 고유벡터 중심성

Engienvector centrality는 주변 노드를 활용해서 노드의 중요성을 나타내는 방법이다.

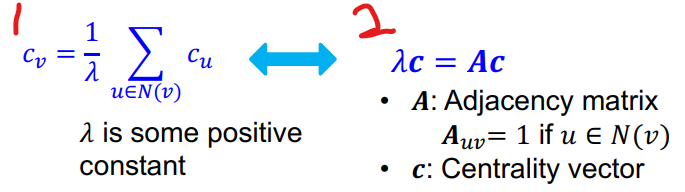
• 노드의 중심성을 1번 식과 같이 재귀적인 방식으로 계산할 수 있다. 1번의 재귀적인 방식을 행렬을 활용한다면 2번과 같이 계산할 수 있다.

• 2번 식을 보면 A는 Grape의 행렬이고 $\lambda$는 고유값을 의미하고 c는 A의 고유벡터를 의미한다. 행렬 A를 가지고 적절한 $\lambda$ 값에 대한 고유벡터 c를 계산하면 이를 노드의 중심성을 나타내는데 사용할 수 있다.

(2) Betweenness centrality - 매개 중심성

Betweenness centrality는 노드들 간의 최단 경로를 통해서 노드의 중요성을 나타내는 방법이다.

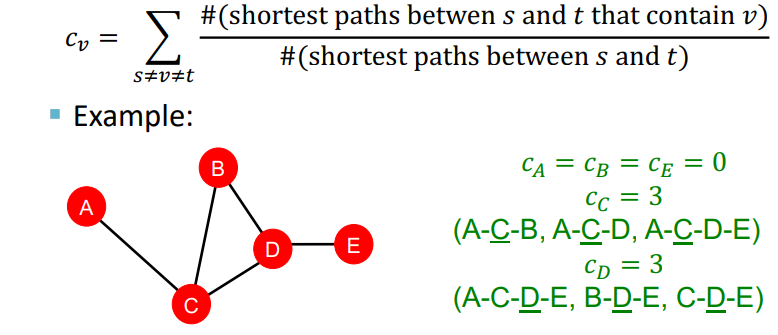
그림에서 A의 노드의 중요성을 나타내고자 할 때 A를 제외한 나머지 노드들의 이동 경로를 봐야한다. C-B, C-D, B-D, C-E, B-E로 가는 모든 이동 경로를 보면 어떠한 경로도 A를 거치지 않기 때문에 A노드의 중요성은 0이 된다. 이와 같은 방식으로 계산을 통해서 각 노드의 중요성을 나타낼 수 있다.

(3) Closeness centrality - 근접 중심성

Closeness centrality는 중요한 노드일수록 다른 노드까지 도달하는 경로가 짧을 것이라는 가정을 가지고 노드의 중요성을 나타내는 방법이다.

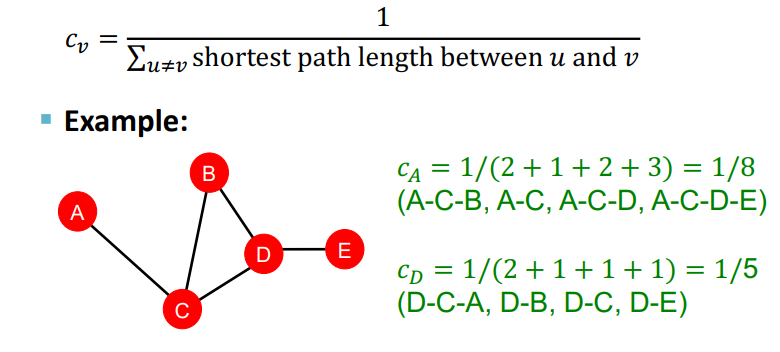
그림처럼 해당 꼭지점의 도달 가능 거리의 총합의 역수를 통해서 나타낼 수 있다.

1-3 Clustering coefficient

Clustering coefficient는 그래프가 얼마나 응집력이 높은지를 알려주는 방법이다.

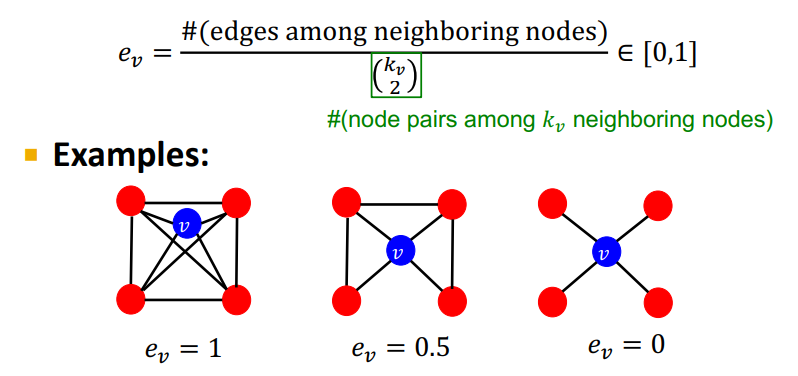
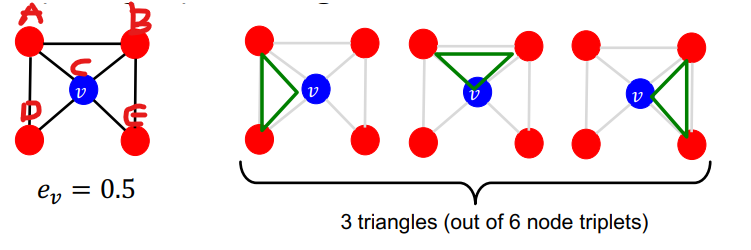
위 그림처럼 연결된 모든 노드 삼중체 중에서 삼각형을 이루는 노드 삼중체를 구해서 계산할 수 있다. 위 그림은 모든 삼중체 A-B-C, A-B-E, A-C-E, A-C-D, B-C-D, B-C-E 중에서 삼각형을 이루는 노드 삼중체가 A-B-C, A-C-D, B-C-E가 존재하기 때문에 0.5로 계산된다.

1-4 Graphlet Degree Vector

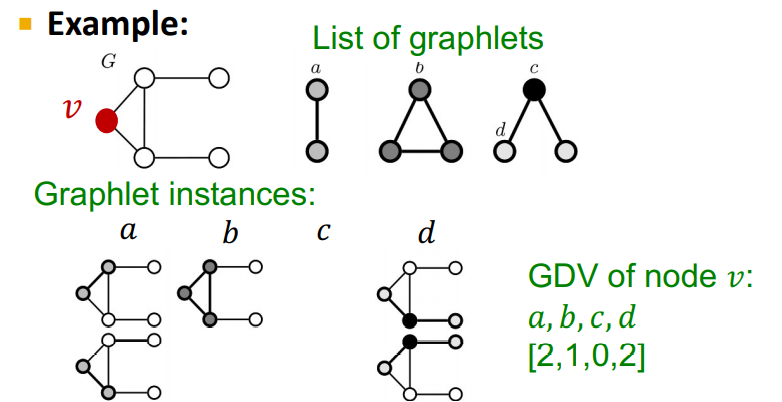
Graphlet Degree Vector는 Graphlet의 개수를 셈으로써 나타내는 표현방법이다. Graphlet Degree Vector를 통해 노드의 국소적인 네트워크의 위상(local network topology)에 대한 measure를 제공할 수 있다.

(1) Graphlet

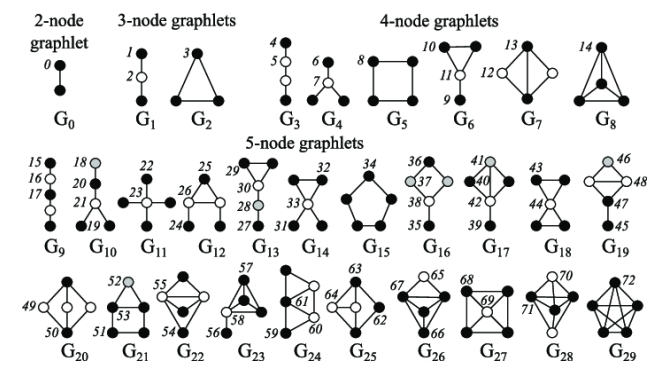
• Graphlet : Rooted connected non-isomorphic subgraphs
  • 그래프의 크기↑ → graphlet의 갯수↑
  • 가령, G1과 G2는 노드의 개수는 같지만, non-isomorphic position에 있음. <- 이런 형태들이 graphlet에 포함됨

Summary

• capture the importance of a node is in a graph (노드의 중요성을 판단하는 방법)

  • Node degree
  • Node centrality
  • 그래프에서 영향력 있는 노드를 찾는데 유용하다. (ex. SNS에서 인플루언서 예측하기)

• Capture topological properties of local neighborhood around a node (구조의 중요성을 판단하는 방법)

  • Node degree
  • Clustering coefficient
  • Graphlet degree vector
  • 그래프에서 노드가 수행하는 특정 역할을 예측하는데 유용하다. (ex. protein-protein interaction network 에서 protein의 기능을 예측하기)

2.Link-level Features

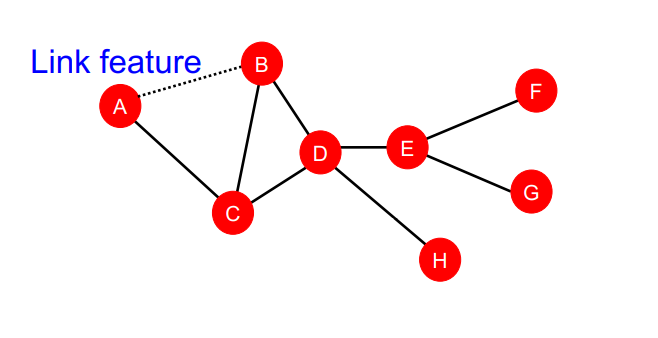
• Link의 feature를 구하는 방법
  • Distance-based feature
  • Local neighborhood overlap
  • Global neighborhood overlap

2-1 Distance-based feature

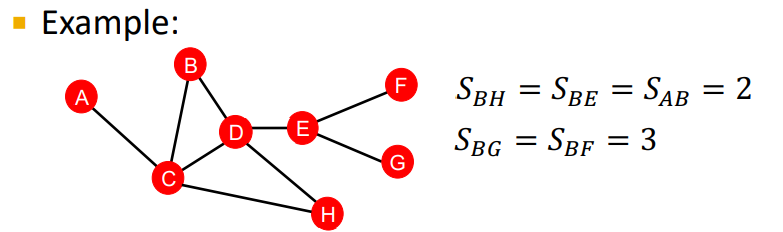
Distance-based feature는 두 노드 간의 최단 거리를 통해 나타난다. 하지만 위 방법은 neighborhood overlap을 반영하지 못한다.
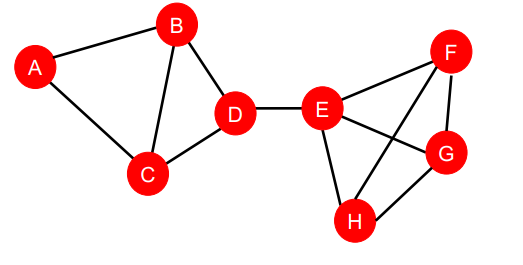
(그림을 보면 B-H를 가는 최단 경로는 2개, B-E를 가는 최단 경로는 1개 하지만 두 노드 간의 링크 모두 같은 숫자로 매핑됨 이렇듯 Distance-based feature 방법은 neighborhood overlap을 반영하지 못함)

2-2 Local neighborhood overlap

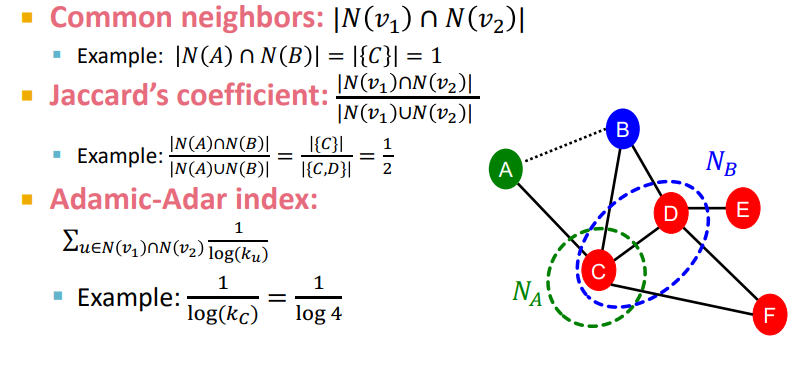
Local neighborhood overlap은 neighborhood overlap을 반영할 수 있는 방법이다. 위 그림 처럼 두 노드 사이에 얼마나 많은 노드를 공유하는지를 통해서 계산할 수 있다.

하지만 Local neighborhood overlap은 위 그림 처럼 두 노드 사이에 공유하는 노드가 없다면 0으로 계산된다는 단점이 존재한다.

2-3 Global neighborhood overlap

Global neighborhood overlap은 전체 그래프를 고려함으로써 Local neighborhood overlap의 단점을 해결한 방식이다.

Global neighborhood overlap은 Katz index(count the number of paths of all lengths between a given pair of nodes)와 adjacency matrix을 활용하여 구할 수 있다.

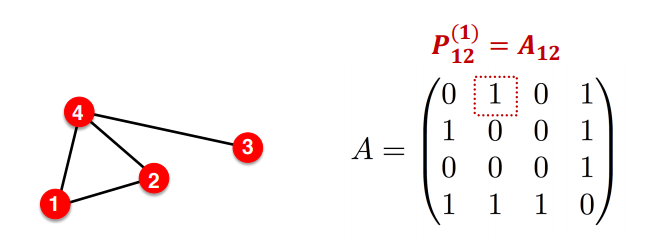
adjacency matrix는 위 그림처럼 각 노드와 노드의 연결을 1과 0으로 표현한 행렬이다. 위 그림은 길이가 1인 adjacency matrix를 표현했다.

위 그림은 길이가 2인 adjacency matrix를 구하는 방법을 나타낸 것이다.

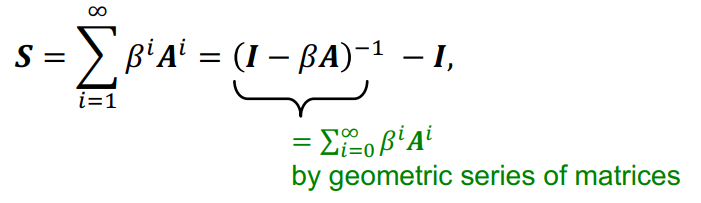
adjacency matrix와 Katz index를 활용하면 모든 길이에 대한 경로의 수를 구할 수 있고 이를 위 그림과 같은 공식을 활용하면 Global neighborhood overlap을 계산할 수 있다.

Summary

• Distance-based feature
  • 두 노드 간의 최단 거리를 통해 나타냄
  • neighborhood overlap을 반영하지 못한다는 단점이 존재
• Local neighborhood overlap
  • 두 노드 사이에 얼마나 많은 노드를 공유하는지를 통해서 계산
  • neighborhood overlap을 반영하지만 두 노드 사이에 공유하는 노드가 없다면 0으로 계산된다는 단점이 존재
• Global neighborhood overlap
  • adjacency matrix와 Katz index를 활용하여 모든 길이에 대한 경로의 수를 구하여 계산
  • Distance-based feature와 Local neighborhood overlap의 단점을 모두 해결할 방법

3.Graph-Level Features

• Graph의 feature를 구하는 방법
  • Graphlet kernel
  • Weisfeiler-Lehman Kernel

Graph Kernels

Graph의 feature를 구하는 방법을 이해하기 위해서는 Graph Kernels에 대하여 우선 알아야 할 필요가 있다. (kernel은 SVM에서 다루는 kernel과 동일함)

Graph Kernels은 두 개의 그래프간의 유사성을 측정하는 방법으로 그 종류로 Graphlet Kernel, Weisfeiler-Lehman Kernel, Random-walk kernel, Shortest-path graph kernel 등등 다양하다.

• Graph Kernels은 graph를 feature로 만드는 것을 목표로함
• Graph Kernels은 그래프를 Bag-of-Words 방식을 활용하여 나타내는 것이 주요 아이디어(BOW는 문서에서 단어의 카운트를 feature로 나타내는 방법)
• Graph Kernels은 Words 대신 Nodes를 사용하여 BOW 방식을 활용
• 아래의 그림 처럼 4개의 동일한 노드를 가지고 있다면 두 다른 그래프는 동일한 feature를 가짐

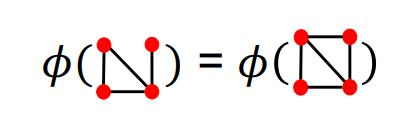
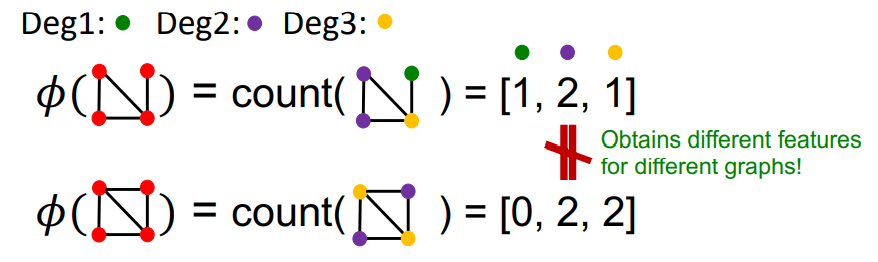
위 그림처럼 node degrees를 사용한다면 다른 노드를 가지고 있기 때문에 두 그래프는 다른 feature를 가지게 된다. 이는 정교한 방법이 아니다.

Graphlet Kernel와 Weisfeiler-Lehman Kernel는 node degrees 보다 더욱더 정교한 방법으로 그래프의 representation을 Bag-of-* 을 사용해 나타낸다. (여기서 * 에 무엇을 사용하느냐가 중요!)

3-1 Graphlet kernel

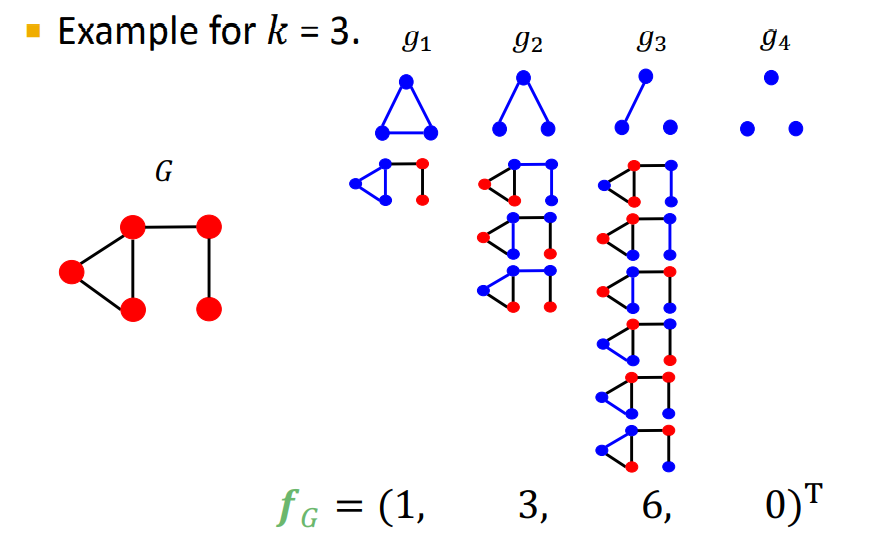
Graphlet kernel은 * 에 Graphlet을 사용하는 방법이다.

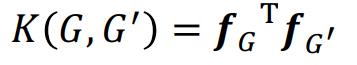
Graphlet kernel은 위와 같은 식으로 계산한다. 그러나 G와 G'의 사이즈가 다르면 값이 크게 왜곡될 수 있다. 따라서 아래와 같은 식을 통하여 정규화를 한다.

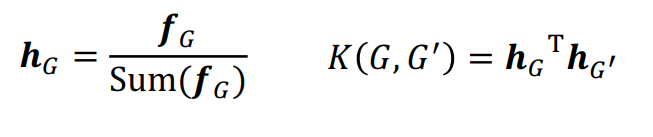
그런데 Graphlet kernel을 Graphlet을 세는 것에 매우 많은 시간과 비용이 들기 때문에 효율적이 방법이 아니다. 따라서 조금 더 효율적인 방법으로 Weisfeiler-Lehman Kernel을 사용한다.

3-2 Weisfeiler-Lehman Kernel

Weisfeiler-Lehman Kernel은 * 에 colors를 사용하는 방법이다.

Color refinement라고 불리는 Algorithm을 활용하여 나타낸다.

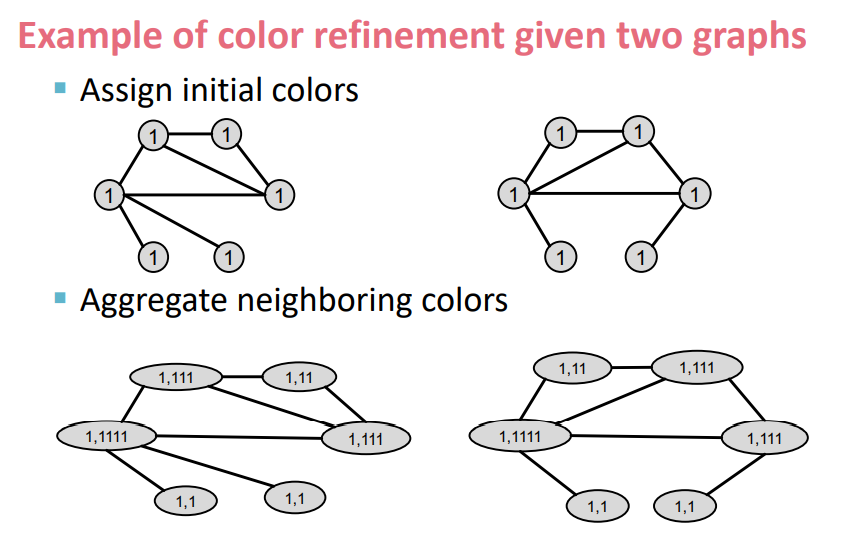
우선 위 그림처럼 colors를 초기화 한 후 인접 노드의 colors를 추가한다.

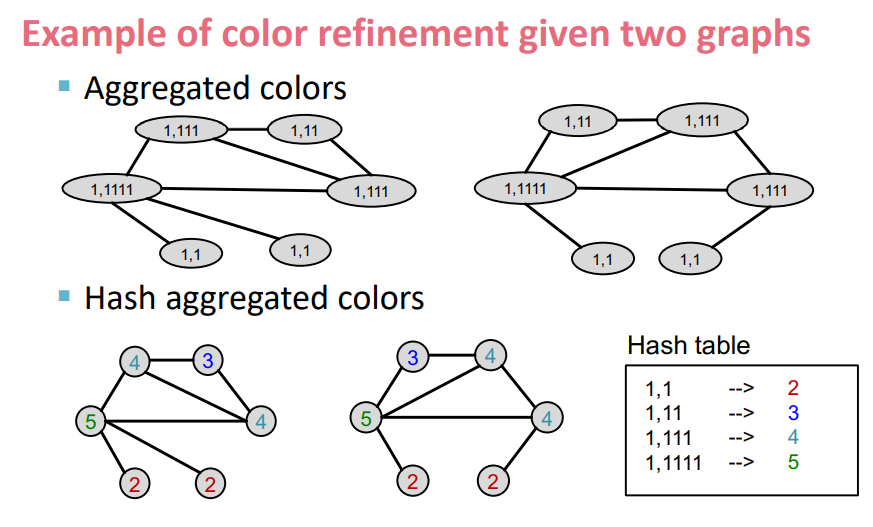
후에 위 그림처럼 Aggregated colors를 Hash table에 새로운 컬러로 맵핑한다.

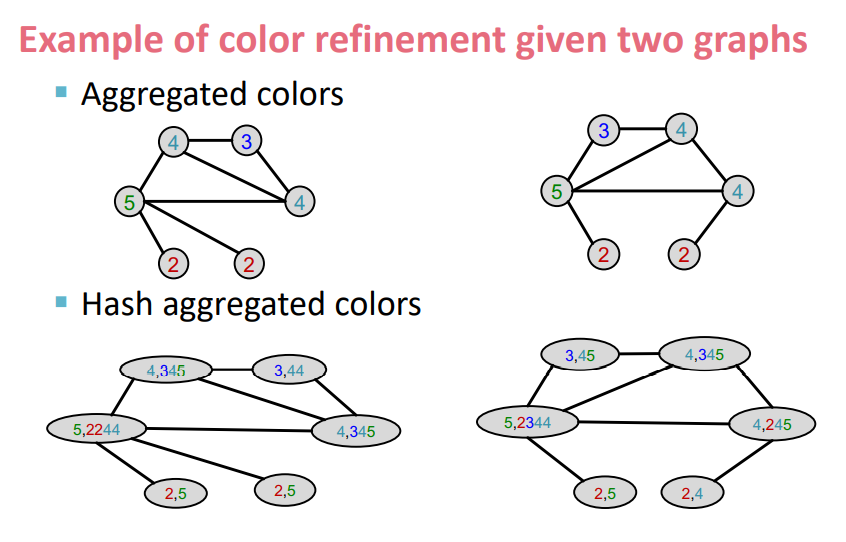
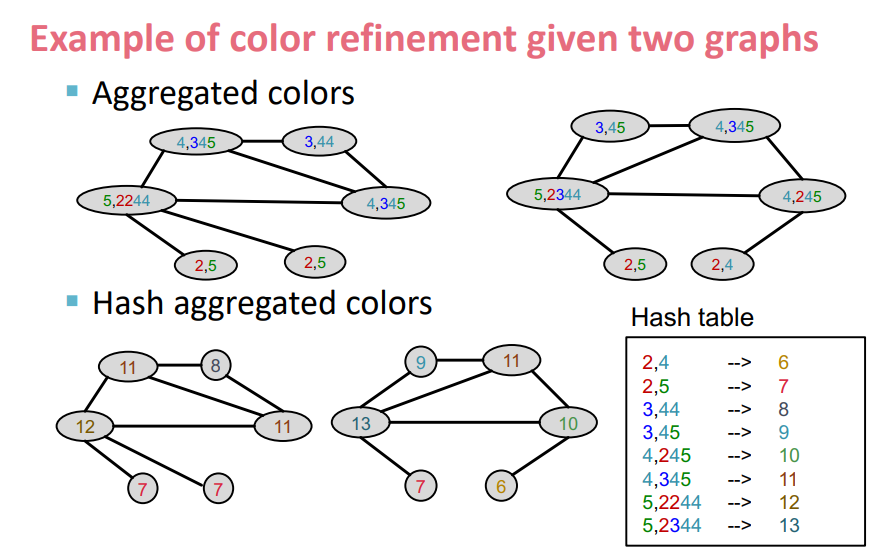
다시 위와 같은 동일한 괴정을 반복한다.

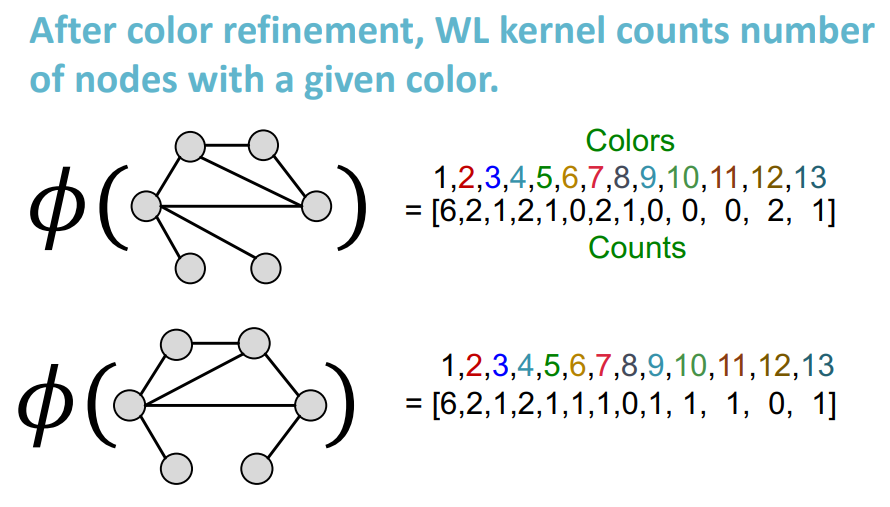
위 그림 처럼 각 colors의 개수를 센다.

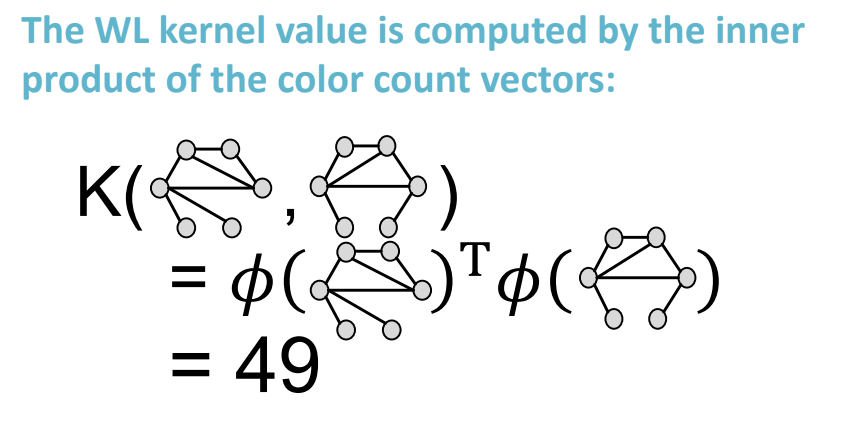
위 그림 처럼 두 color count vectors를 내적하면 WL kernel value를 계산할 수 있다.

Weisfeiler-Lehman Kernel은 시간 복잡도가 선형이기 때문에 Graphlet kernel보다 매우 효율적인 방법이다.

Summary

• Graphlet Kernel
  • Bag-of-graphlets
  • 시간과 비용이 많이드는 매우 비효율적인 방법
• Weisfeiler-Lehman Kernel
  • Bag-of-colors
  • Color refinement Algorithm 사용
  • 시간복잡도가 선형인 효율적인 방법
  • 우리가 앞으로 다룰 GNN과 매우 밀접한 방법

참고자료

• https://bab2min.tistory.com/554
• https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/07/network/
• https://ratsgo.github.io/data%20structure&algorithm/2017/11/18/graph/
• https://data-weirdo.github.io/data/2020/08/31/data-graph-03.motifs/