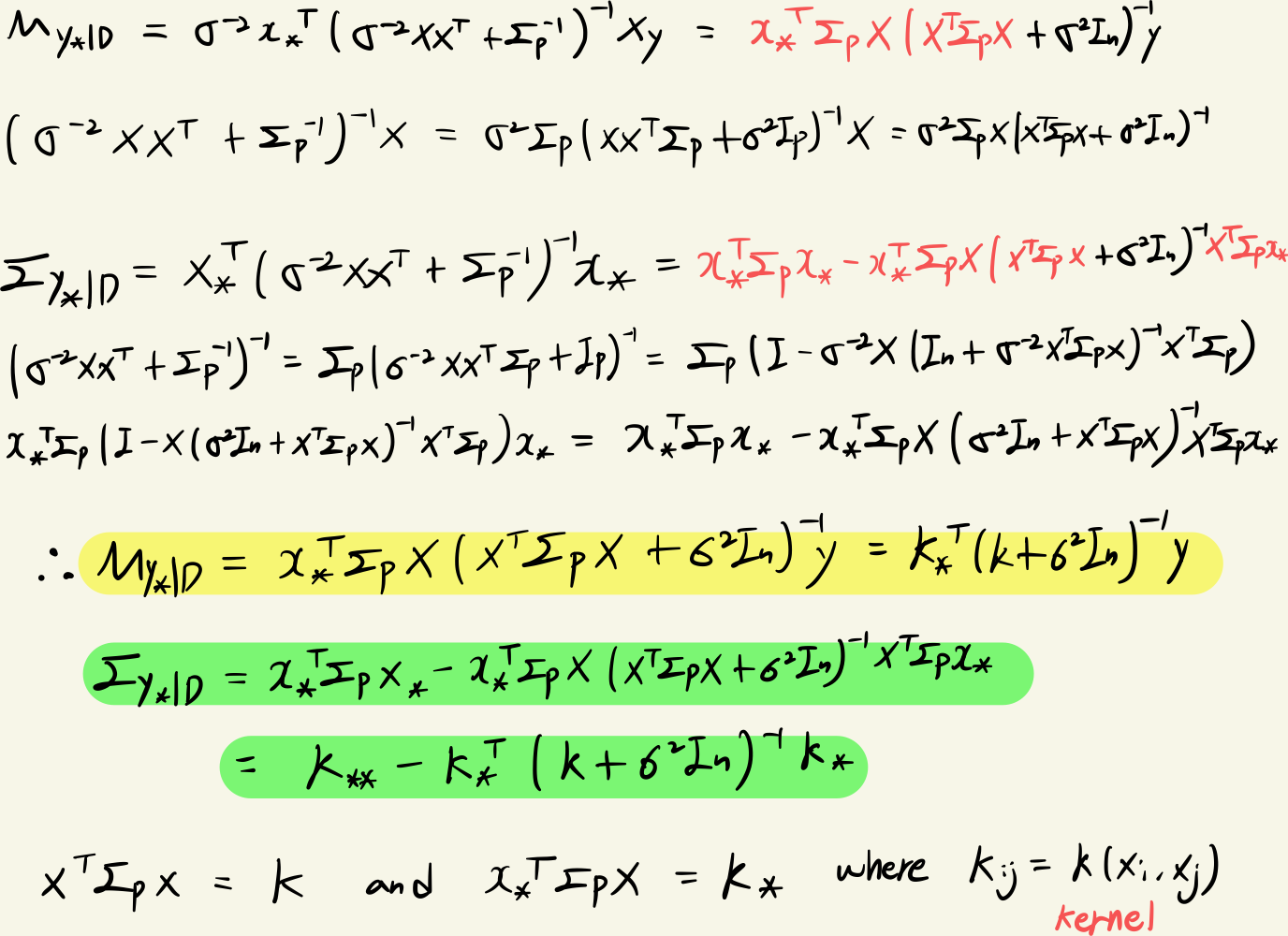2주차 - Gaussian Process
Gaussian Basics
Gaussian random variable X∼N(μ,Σ)
-
P(X;μ,Σ)=(2π)d/2∣Σ∣1e−21((x−μ)TΣ−1(x−μ)) - prbability density function
-
∫xP(X;μ,Σ)dx=1
-
P(XA)=∫XBP(XA,XB;μ,Σ)dXB - marginalization
-
P(XB)=∫XAP(XA,XB;μ,Σ)dXA - marginalization
-
P(XA∣XB)=∫XBP(XA,XB;μ,Σ)dXBP(XA,XB;μ,Σ) - conditioning
-
XA∣XB=XB∼N(μA+ΣABΣBB−1(XB−μB),ΣAA−ΣABΣBB−1ΣBA)
Multivariate Gaussian
X=[XAXB],μ=[μAμB],Σ=[ΣAAΣBAΣABΣBB],Σ=E[(Xi−μi)(Xj−μj)]

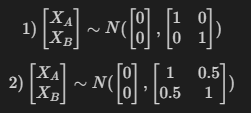
covariance matrix는 변수간 상관관계에 대한 정보를 담고있다.
몇 가지 중요한 특징들
- Σ is positive semi-definite
- Σii=Var(yi),Σii>=0
- if Yi,Yj are independent , Xi is very different from Xj →Σij,Σji=0
- if Xi≈Xj,Σij,Σji>0
Example - Predict House price
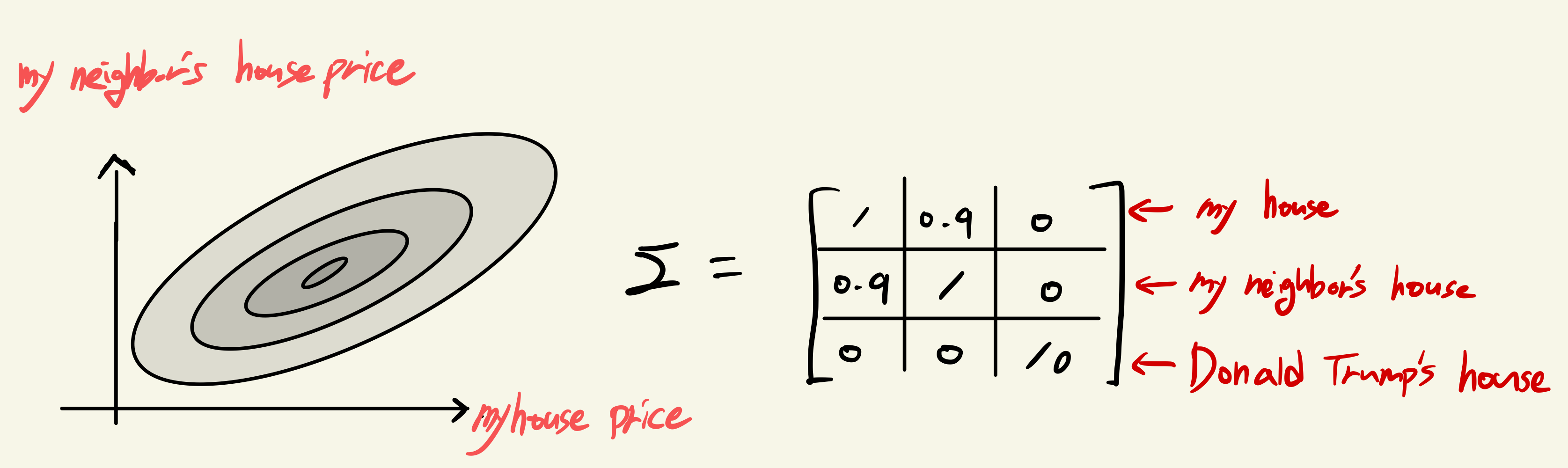
GP Regression
 - 일반적인 Linear regression
- 일반적인 Linear regression
2 different ways to learning parameter W
D={(x1,y1),....,(xn,yn)}
1) MLE: P(D;w)=∏i=1nP(yi∣xi;w) - probability of data given parameters
2) MAP: P(w∣D)∝P(D∣w)P(w) - given our data, what is most likely set of parameters
Once gaussian always gaussian
Assume a Gaussian Noise ϵ∼N(0,σ2), P(yi∣xi;w)=N(wTx,σ2I)
P(w)=N(0,Σp)
∴P(D;w),P(w∣D)는 모두 Gaussian
일반적인 machine learning process:
D→W→y=WTX (데이터를 학습시켜 파라미터 W를 추정하고 예측모델에 테스트 데이터를 입력하여 예측을 수행.)
MLE와 MAP에서는 하나의 특정 parameter w에 대한 predictive model을 준다.
Bayesian says.. Instead of model the probability of w (and we do prediction for that w), why don’t we from the start from modeling the prediction of the test point.
-
P(y∣x∗,D): given the test set of x, what is distribution of label y?
-
P(y∣x,D)=∫wP(y,w∣D,x)dw=∫wP(y∣w,D,x)P(w∣D)dw
marginalize out the model: average the prediction overall possible parameter W's with weight P(W∣D)
P(y∣x,D)=∫wP(y,w∣D,x)dw=∫wP(y∣w,x) P(w∣D)dw
P(y∣w,x): Gaussian
P(w∣D): Gaussian
P(y∣x,D)→Gaussian (Once gaussian always gaussian)
하지만, 위의 integral식은 closed form으로 풀리지 않는다. 그러나, Gaussian likelihood and prior assumption을 통해 P(y∗∣x∗,D)는 여전히 gaussian이기에 우리는 이 문제를 풀 수 있다. 왜냐하면, 우리는 gaussian의 형태를 잘 알고 있기 때문 !
P(y∗∣x∗,D)∼N(μy∗∣D,Σy∗∣D)
Y∗∣(Y1=y1,...,Yn=yn,x1,...,xn,xt)∼N(K∗T(K+σ2I)−1y,K∗∗−K∗T(K+σ2I)−1K∗)
Example - Gaussian Process
 where there is data you should be confident, when you don't have data you should believe on your prior knowledge.
where there is data you should be confident, when you don't have data you should believe on your prior knowledge.
Gaussian Process Math
Assuming that w∼N(0,Σp) P(W∣D)∼N(σ−2A−1Xy,A−1) where A=σ21XXT+Σp−1
prediction Y∗ for a testing sample X∗
P(y∗∣x∗,D)∼N(μy∗∣D,Σy∗∣D)
where μy∗∣D=σ−2x∗TA−1Xy , Σy∗∣D=x∗TA−1x∗
From the property of matrix inversion lemma,
(I+UV)−1U=U(I+VU)−1
(I+UV)−1=I−U(I+VU)−1V
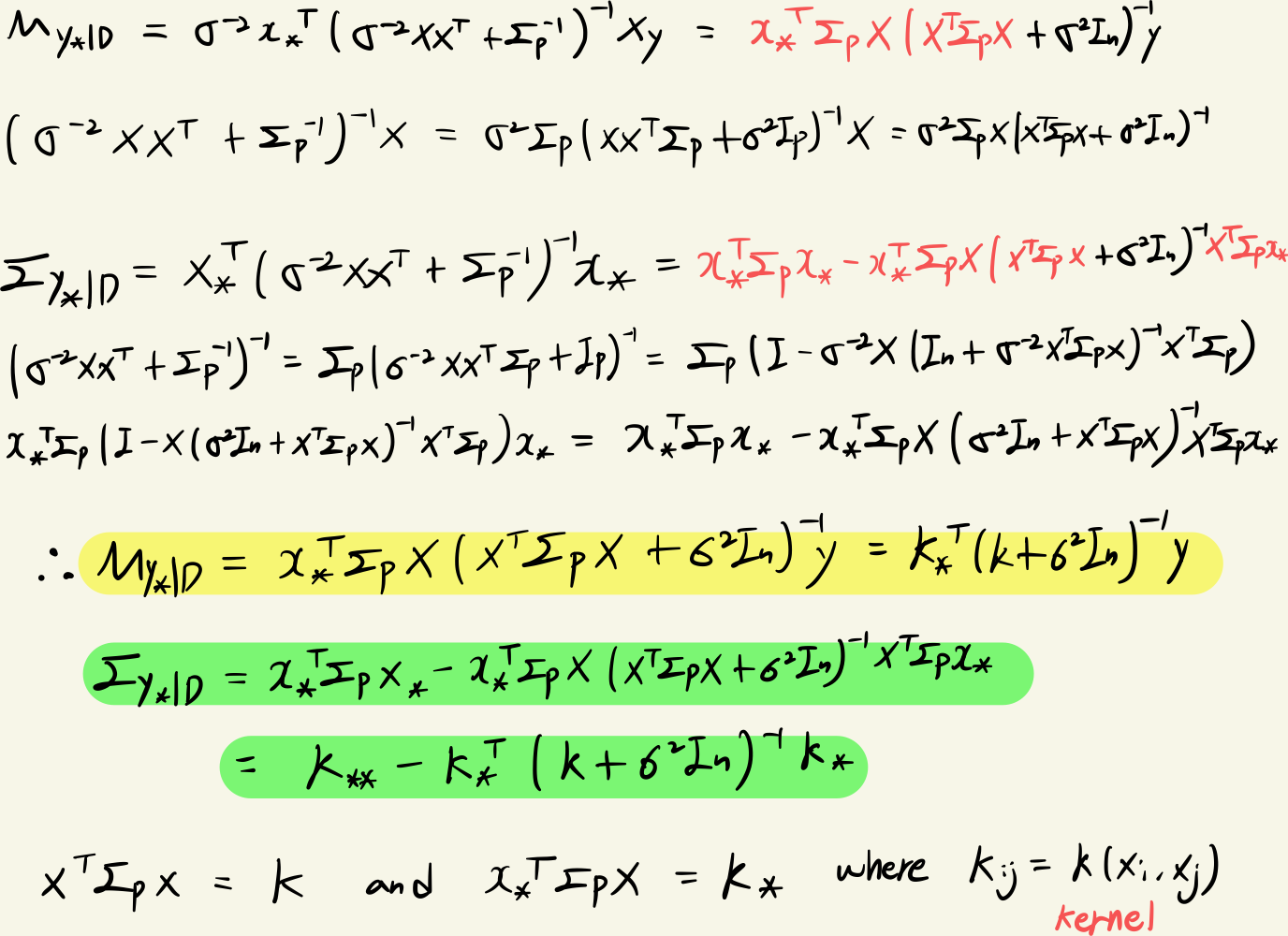
Kernel

위의 그림처럼 linear model f(x)로 문제를 풀 수 없을 때, input space X를 linear model이 해결할 수 있는 형태인 고차원의 feature space ϕ(X) 로 만들면 문제를 해결할 수 있다.
하지만, ϕ(X)를 정의하는 것 자체가 어렵거나 ϕ(X)를 푸는 연산량이 많은 문제점이 발생. 이를 해결하고자 Kernel을 적용한다.
ex) polynomial kernel
ϕ(x)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛1x1..xdx1x2..xd−1xd..x1x2...xd⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
→ϕ(x)Tϕ(z)=1+x1z1+x2z2+...+x1..xdz1...zd=∏k=1d(1+xkzk)
계산비용을 2d에서 kd로 줄일 수 있다. K(xi,xj)=ϕ(xi)Tϕ(xj)=Kij
GP에서는 RBF Kernel 주로 사용
Σij=K(xi,xj)=γeσ2−∣∣xi−xj∣∣2
we can decompose Σ as (KK∗TK∗K∗∗)
kernel matrices K,K∗,K∗∗ are functions of x1,x2,..xn,x∗
kernel is well defined covariance function
따라서 우리는 Gaussian Process를 평균과 공분산 kernel로 나타낼 수 있다.
y∼GP(m(x),k(x,x′))

Once you've constructed these matrices of similarities (K,K∗,K∗∗), the process of prediction is just computing the posterior distribution of f∗.
P(y∗∣x∗,D)∼N(μy∗∣D,Σy∗∣D)
Since I have a gaussian distribution of x∗, I can draw samples from gaussian.
Gaussian Process 정리
y=WTx+ϵ→ Noisy ϵ∼N(0,σ2)
Function evaluation에 Noise가 있는 Noisy GP regression을 정의
P(y∣x,D)=∫wP(y∣w,D,x)P(w∣D)dw
X가 given 되어있을 때, y의 distribution을 계산하기 위해 w로 marginalize
W∼N(0,Σp)
P(W∣D)∼N(σ−2A−1Xy,A−1) where A=σ21XXT+Σp−1
Prior를 Gaussian으로 가정. covariance matrix는 similarity kernel(RBF)로 계산
P(y∣w,D,x)=∏i=1nP(yi∣xi;w)
관측된 모든 데이터 포인트들에서의 추정값은 iid를 가정하기 때문에 전부 곱해서 계산. 역시 gaussian을 따름.
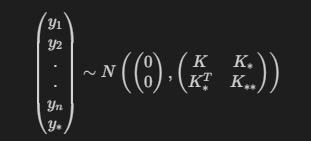
P(y∗∣x∗,D)∼N(μy∗∣D,Σy∗∣D)
μ∗=K∗T(K+σ2I)−1y
Σ∗=K∗∗−K∗T(K+σ2I)−1K∗
이제 새로운 x∗데이터가 들어왔을 때, y의 covariance matrix가 어떻게 생겼는지 알 수 있고 평균과 분산을 활용하여 예측 모델을 만들어 낼 수 있음.
GPs are elegant and powerful ML method.
We get a measure of uncertainty for predictions for free.
GPs work very well for regression problems with small training data set sizes.
Running time O(n3) due to matrix inversion. thus, GPs get slow when n >> 0.
Reference
https://www.youtube.com/watch?v=R-NUdqxKjos&t=1s - Cornell대학 Kilian교수님 강의
https://www.edwith.org/bayesiandeeplearning/joinLectures/14426 - edwith 최성준님 강의
https://www.youtube.com/watch?v=4vGiHC35j9s - UBC Nando de Freitas교수님 강의
https://www.youtube.com/watch?v=MfHKW5z-OOA - UBC Nando de Freitas교수님 강의

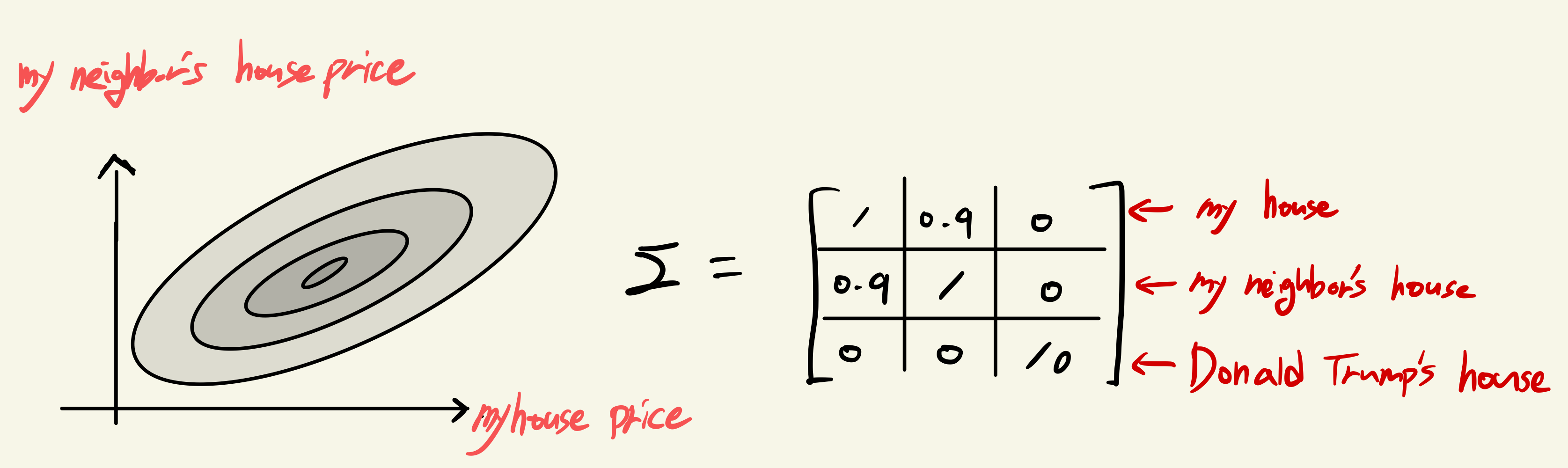
- 일반적인 Linear regression
 where there is data you should be confident, when you don't have data you should believe on your prior knowledge.
where there is data you should be confident, when you don't have data you should believe on your prior knowledge.