[알고리즘 공부] 퀵 정렬(Quick Sort)

김현정·2025년 3월 6일

CS - 알고리즘

목록 보기

4/5

퀵 정렬(Quick Sort)

퀵 정렬은 분할정복(divide and conquer) 방법을 통해 주어진 배열을 정렬한다.
퀵 정렬은 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다. 또한 병합 정렬과 달리 퀵 정렬은 배열을 비균등하게 분할한다.

분할 정복(divide and conquer) 방법 :
문제를 작은 2개의 문제로 분리하고 각각 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.

Process

배열 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗(pivot)이라고 한다.
피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 배열을 둘로 나눈다. 이렇게 배열을 둘로 나누는 것을 분할(Divide)이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
분할 된 두 개의 작은 배열에 대해 재귀(Recursion)적으로 이 과정을 반복한다.

재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

Java Code

퀵 정렬은 다음의 단계들로 이루어진다.

정복 (Conquer)

부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.

public void quickSort(int[] array, int left, int right) {
    if(left >= right) return;
    
    // 분할 
    int pivot = partition(); 
    
    // 피벗은 제외한 2개의 부분 배열을 대상으로 순환 호출
    quickSort(array, left, pivot-1);  // 정복(Conquer)
    quickSort(array, pivot+1, right); // 정복(Conquer)
}

분할 (Divide)

입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열 (피벗을 중심으로 왼쪽 : 피벗보다 작은 요소들, 오른쪽 : 피벗보다 큰 요소들)로 분할한다.

public int partition(int[] array, int left, int right) {
    /**
    // 최악의 경우, 개선 방법
    int mid = (left + right) / 2;
    swap(array, left, mid);
    */
    
    int pivot = array[left]; // 가장 왼쪽값을 피벗으로 설정
    int i = left, j = right;
    
    while(i < j) {
        while(pivot < array[j]) {
            j--;
        }
        while(i < j && pivot >= array[i]){
            i++;
        }
        swap(array, i, j);
    }
    array[left] = array[i];
    array[i] = pivot;
    
    return i;
}

Quick Sort 개선

partition() 함수에서 피벗 값이 최소나 최대값으로 지정되어 파티션이 나누어지지 않았을 때, O(n^2)에 대한 시간복잡도를 가진다.

즉 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정령되어있으면 0(n^2)의 시간복잡도를 가진다. 이때, 배열에서 가장 앞에 있는 값과 중간값을 교환해준다면 확률적으로나마 시간복잡도 O(nlog2n)으로 개선할 수 있다. 하지만, 이 방법으로 개선한다고 해도 퀵 정렬의 최악의 시간복잡도가 O(nlog2n)가 되는 것은 아니다.

Gif로 이해하기

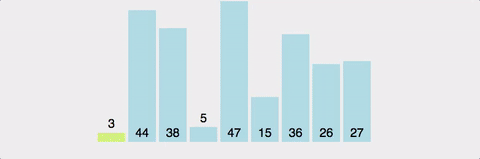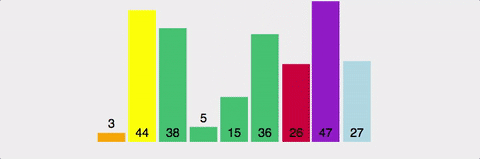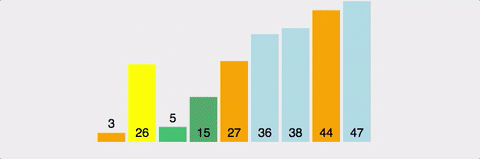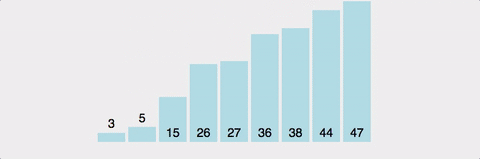
시간복잡도

최선의 경우(Best cases) : T(n) = O(nlog2n)

비교 횟수 (log2n)

레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k) 했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다.

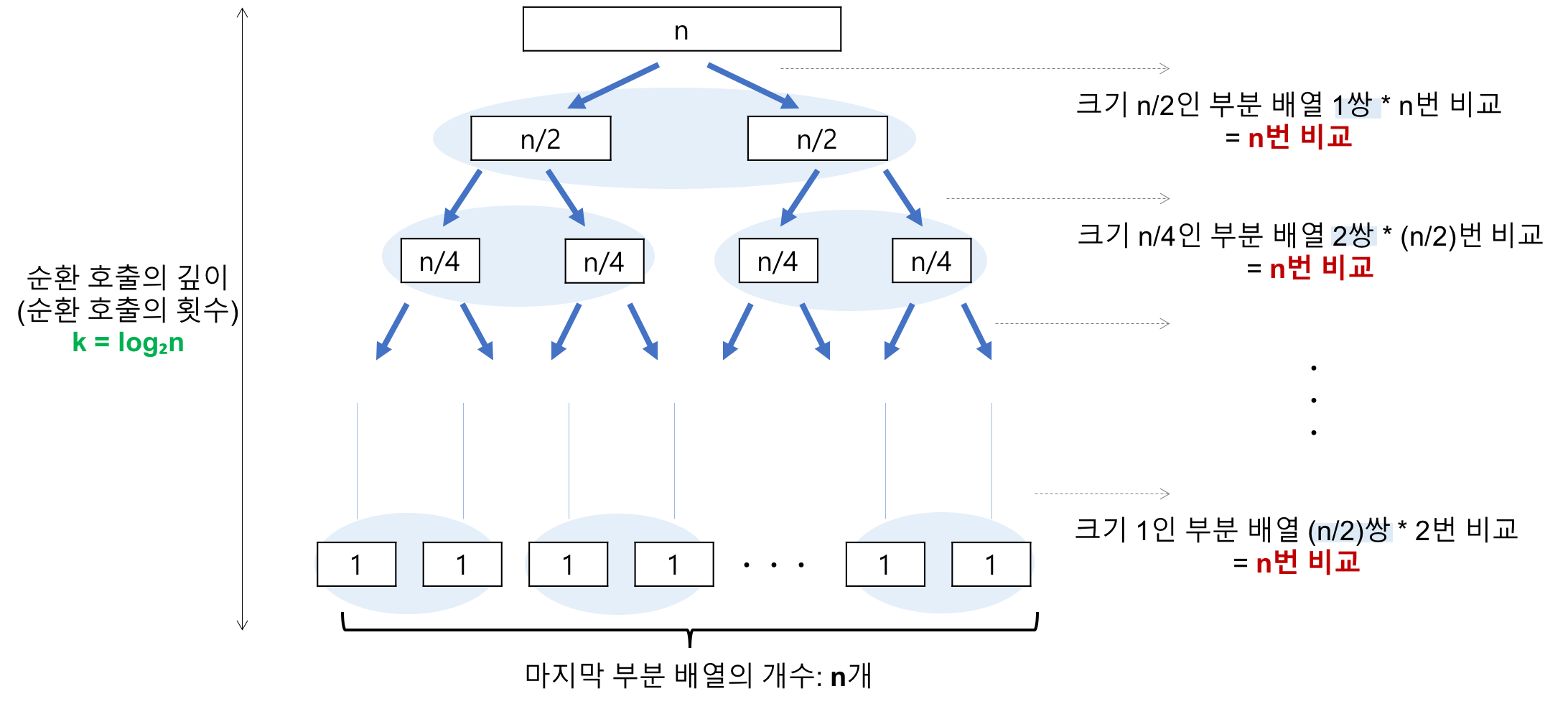
이것을 일반화하면 n=2^k의 경우, k(k=log2n)임을 알 수 있다.

각 순환 호출 단계의 비교연산(n)

각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
따라서 최선의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog2n가 된다.
이동 횟수는 비교횟수보다 적으므로 무시할 수 있다.

최악의 경우(Worst cases) : T(n) = O(n^2)

최악의 경우는 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정렬되어있는 경우다.

비교 횟수 (n)

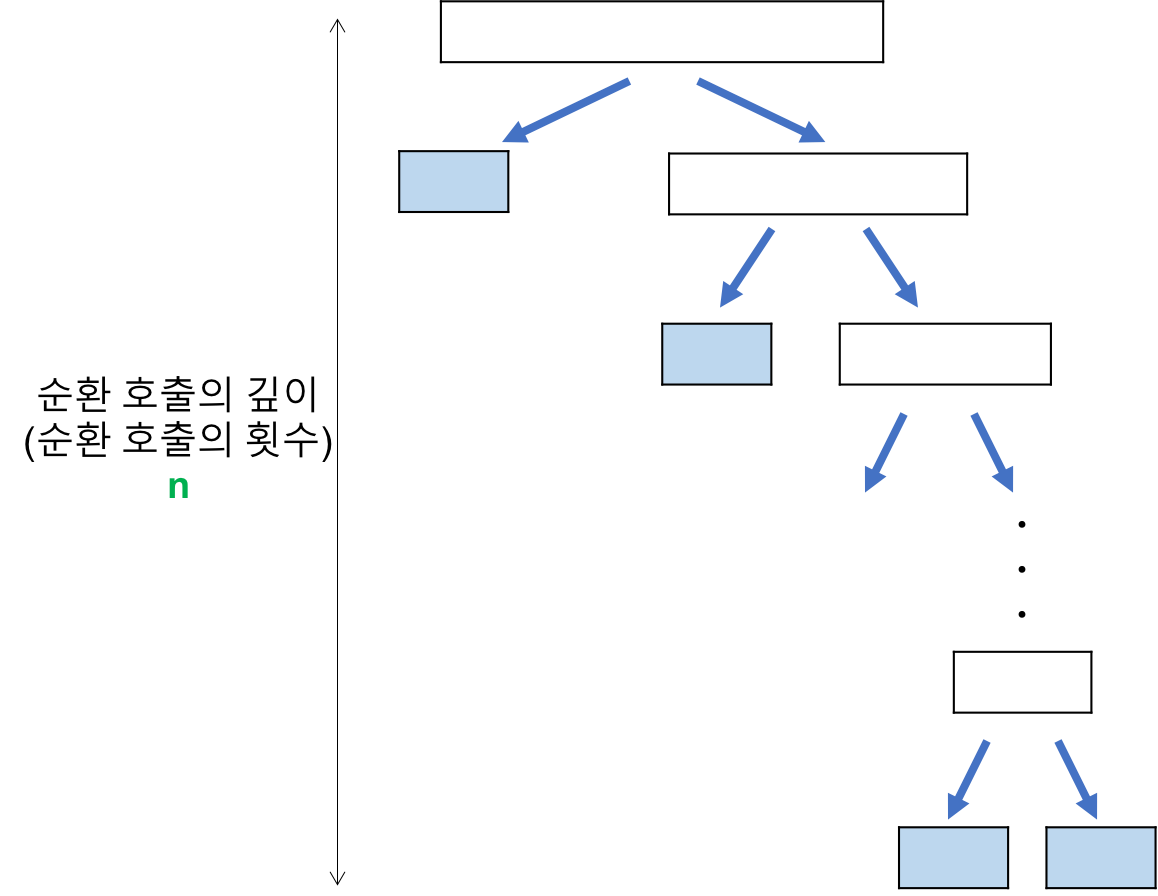
레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n임을 알 수 있다.
각 순환 호출 단계의 비교연산 (n)
각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균n번정도의 비교가 이루어진다.

따라서, 최악의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2다.
이동 홧수는 비교 횟수보다 적으므로 무시할 수 있다.

평균의 경우(Average cases) : T(n) = O(nlog2n)

공간복잡도

주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n)이다.

장점

불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문에, 시간 복잡도가 O(nlog2n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다.