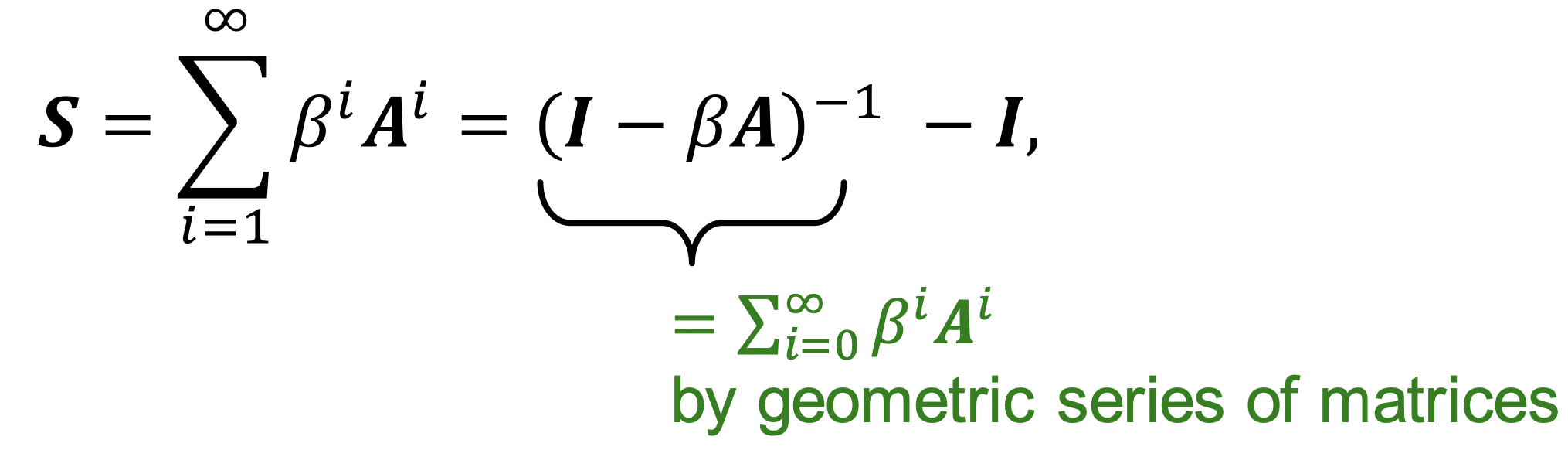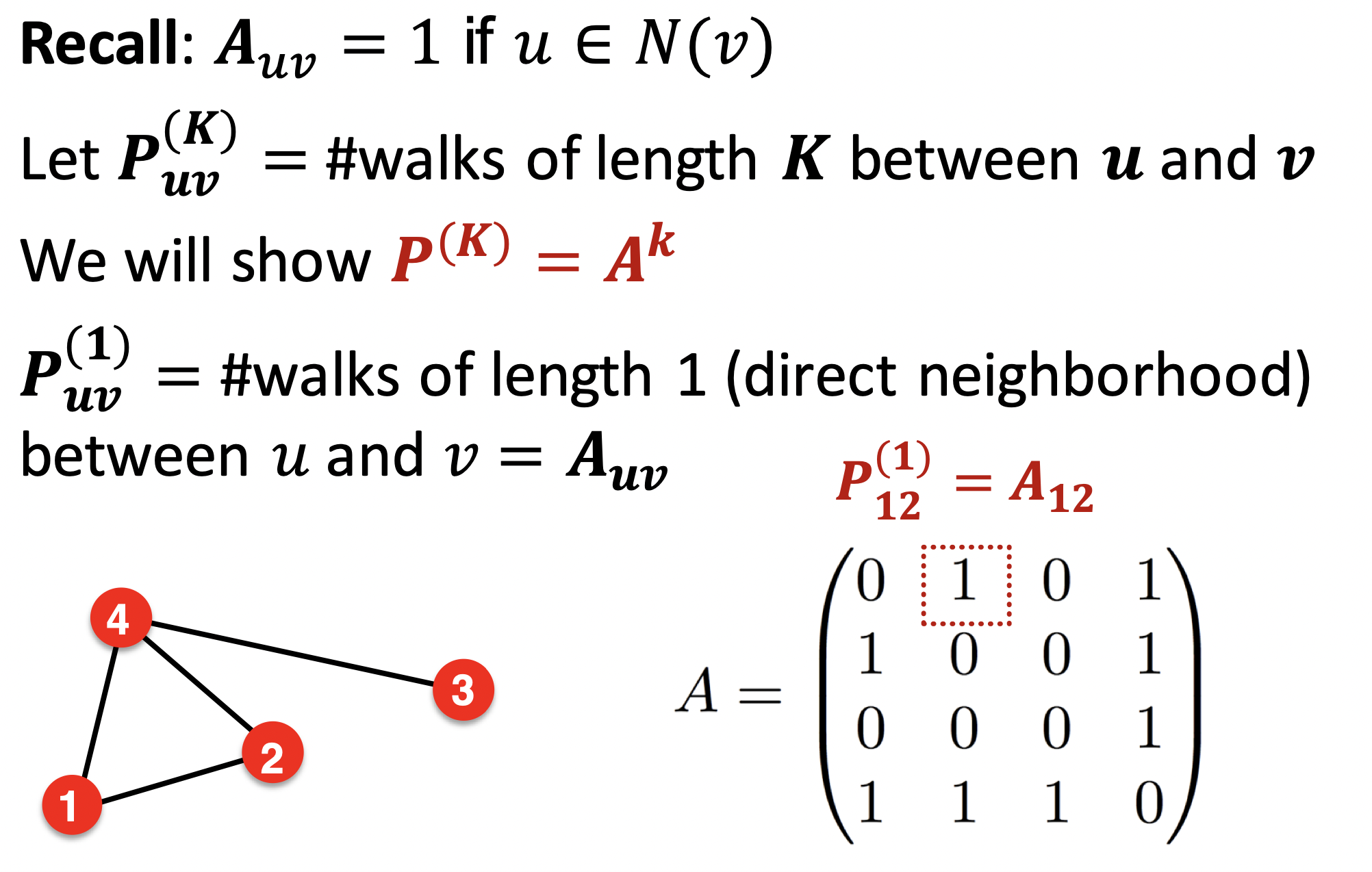Link Prediction tasks and Features

---

1. Link-level Prediction 이란?

기존의 Link에 기반해서 새로운 Link를 예측 하는 것을 의미합니다.
새로운 Link를 예측하는 방법에는 크게 두가지가 있습니다.

• Random LInk를 지우고 학습하는 방법
• 시간이 지나면서 생기는 Link를 예측하는 방법

첫 번째 방법은 Protein구조 와 같이 이미 충분히 복잡하게 얽혀져 더이상 graph의 변화를 기대하기 힘든 경우 사용합니다.
두번째 방법은 시간이 지남에 따라 link상태가 변하는 인간관계 network 등에서 사용합니다.

전체 graph에서 두 Node pair (x,y)를 뽑아 두 Node관의 score c(x,y)를 계산하고 실제로 Node간에 Link가 생겼는지 관찰합니다.

2. Link-level Features

Link-level의 features로는 크게 3가지로 구분 할 수 있습니다.

Distance-based Features
두 노드간의 최단거리의 갯수를 의미합니다.

그러나 이 Features로는 Neighborhood가 얼마나 겹치는지를 표현 할 수 없었습니다.

Local Neighborhood overlap
두 노드 $v_{1}$ 과 $v_{2}$간에 공유하는 이웃 노드들의 갯수를 세는 방법 입니다.

• Common neighbors
  $|N(v_{1}) \cap N(v_{2})|$
  단순하게 공통된 이웃 노드들의 갯수를 새는 방법입니다.
• Jaccard's coefficient
  $|N(v_{1}) \cap N(v_{2})|\over|N(v_{1})\cup N(v_{2})|$
  전체 연결된 노드들 중 공통된 이웃 노드들의 비율입니다.
• Adamic-Adar index
  $\sum_{u\in N(v_{1}) \cap N(v_{2})}$ $1\over log(k_{u})$
  공통된 이웃 노드들의 degree의 합 입니다.

  Limitation
  
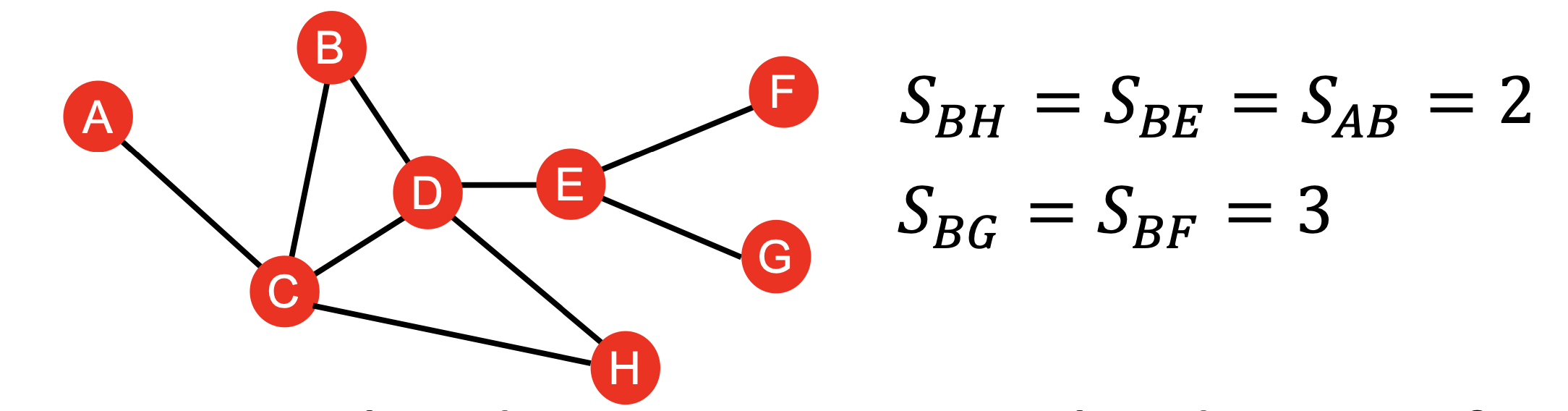
  두 노드가 공통된 이웃 노드를 가지지 않는다면 위 계수들은 항상 0이 되게 됩니다.
  하지만 예시에서 보듯이 A 와 E 는 여전히 잠재적으로 연결 될 가능성이 있습니다.

Global Neighborhood overlap

• katz index
  주어진 두 노드사이를 모든 길이로 갈 수 있는 방법의 수의 합 입니다.

  
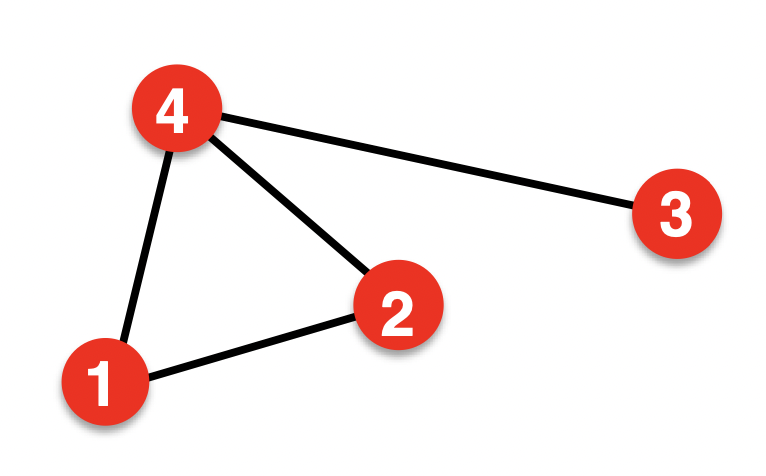
  예를 들어 1번 노드에서 2번 노드로 길이 1로 가는 방법은 1가지 입니다.
  마찬가지로 길이 2로 가는 방법은 1가지 입니다.
  이제 길이 3, 4, 5 ... 로 가는 방법의 가지수를 전부 합한 계수입니다.

3. katz index의 계산

Global Neighborhood overlap은 전체 그래프를 고려하기 때문에 local neighborhood overlap의 한계를 극복 할 수 있습니다.

그렇다면 어떻게 두 노드사이를 건너는 방법의 가짓수를 샐 수 있을까요?

바로 adjacency matrix를 이용합니다.

$P^{(K)}$는 두 노드 $uv$사이를 길이 K로 건너가는 방법의 가짓 수 입니다.

A를 원하는 길이 K만큼 곱하여 adjcency matrix를 읽어 $P^{(K)}$를 읽어냅니다.

다시 kats index로 돌아오겠습니다.
kats index는 모든 길이에 대해 P를 더해주어야 합니다.

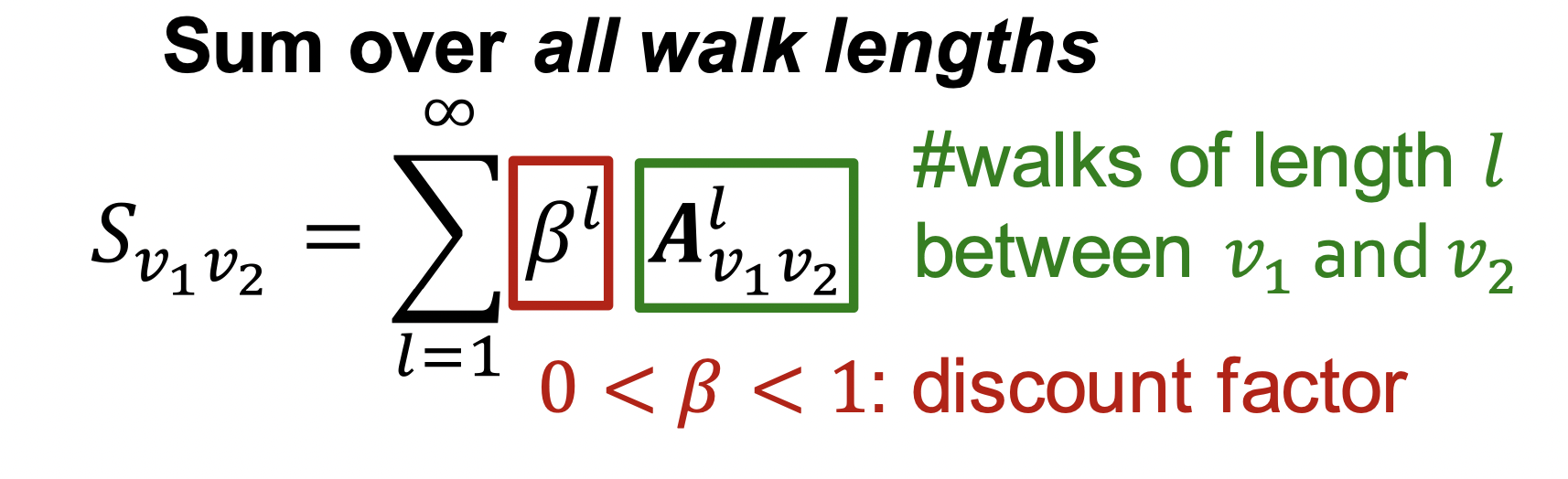
위 식은 이제 closed-form으로 변형하여 계산이 가능합니다.