Scaled Dot-Product Attention
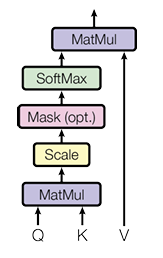
Fig 1. Scaled Dot-Product Attention
- query와 key에 대한 임베딩 벡터 크기는 dk. value에 대한 임베딩 벡터 크기는 dv.
- 따라서 query, key, value 토큰 하나에 대한 임베딩 벡터 크기는 dk, dk, dv. 엄밀히 말하면 1×dk 이다.
- 전체 토큰 개수는 N이라 하면, 토큰 하나에 대해서 1×dk였으니 N개의 벡터를 모아놓으면 행렬이 된다. 따라서 query 행렬 Q는 N×dk
Key 행렬 K는 N×dk
Value 행렬 V는 N×dv
수식에 들어가기 앞서, 예를 들어보자. 그는 고양이를 좋아한다에서 토큰은 그는, 고양이를, 좋아한다라고 해보자.
이제 여기서 쿼리 그는이 전체 문장과 얼마나 관련있는지를 알기 위해 dot-product를 사용한다.
(1×dk)×(dk×N)=1×N. 이 값이 그는이 전체 문장에서 가지는 어텐션 스코어이고, 이 어텐션 스코어를 값(V)에 곱한 것이 어텐션 값이다 (1×dk)×(dk×N)×(N×dv) = (1×dv).
그러면 전체 문장의 전체 문장에 대한 어텐션 값을 계산해보면 QKTV = (N×dk)×(dk×N)×(N×dv)=(N×dv)
자, 이제 수식으로 가보자
Attention(Q,K,V)=softmax(dkQKT)V
여기서 이제 softmax(dkQKT)부분과 V부분을 분리해야한다. 소프트맥스 부분은 어텐션 스코어를 계산하는 부분이고, 그렇게 계산한 어텐션 스코어를 값(V)에 곱해주는 것이다.
논문에서는 dk로 스케일링하고 소프트맥스함수를 취해 0~1로 정규화한 것이다.
Multi-Head Attention
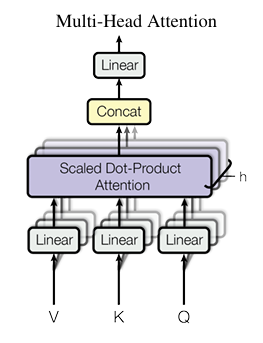
Fig 2. Multi-Head Attention
멀티헤드 어텐션은 Scaled Dot-Product Attention을 확장한 것에 가깝다. 여러 개의 Scaled Dot-Product Attention을 수행하고 그것을 이어붙인것이기 때문이다.
즉, 앞에서 수행한 Scaled-Dot Product Attention은 하나의 대해서 수행한 것이다.
MultiHead(Q,K,V)=Concat(head1,...,headh)WOwhere headi=Attention(QWiQ,KWiK,VWiV)
그림에서 Q,K,V가 들어가는 Linear가 WiQ,WiK,WiV를 의미하는 것이다.
이를 통해, 서로 다른 위치에 있는, 서로 다른 표현공간(representation subspaces)의 정보에 동시에(jointly) 집중할 수 있게 해준다.


