참고:
퀀트투자를 위한 머신러닝, 딥러닝 알고리즘 트레이딩
https://neptune.ai/blog/evaluation-metrics-binary-classification
분류 문제는 범주형 결과(카테고리) 변수를 갖는다. 따라서 관측이 특정 클래스에 속하는지를 맞추는 것이 목표가 된다. 이 때 모델은 분류에 사용할 점수를 계산해 주고, 특정 임계값을 기준으로 범주를 분류하게 된다.
일반적으로, binary분류의 경우 나온 점수를 0혹은 1로 바꾸거나, 정규화를 시킨다.
각가의 예측 결과에 대해 그것이 참인지 거짓인지에 따라, confusion matrix를 만들 수 있다.
분류 문제에 대해 모델을 만드는 목적은 이 분류에 사용되는 임계값을 적절하게 선택하는 데에 있게 된다.

출처: http://piramvill2.org/?p=2935
이를 바탕으로 많은 평가 metric들이 있다.
정확도. 전체 경우의 수 중에서 예측과 정답이 같은 것들의 비율이다.
FPR(False Positive Rate = type1 error=alpha) 귀무가설이 실제로 참이지만 귀무가설을 기각하는 오류.(즉 실제가 False인데 True로 예측.). 예를 들어 스팸이 아닌 메일이 스팸메일함에 들어가는 경우.
: 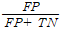
FNR(False Negative Rate = type2 error=beta) 귀무가설이 실제로 거짓이지만 귀무가설을 참이라고 생각하는 것. 예를 들어 스팸메일이 메일함에 스팸메일함에 안 보내지는 경우.
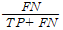
type1 error는 p value로 써 매우 쉽게 다뤄지는데, type2 또한 매우 중요하다. 예를 들어, 카드 거래에서 거짓 거래를 찾는 것을 생각하면, 제대로 된 거래를 거짓 거래로 분류했을 때의 비용과 거짓 거래를 찾지 못 했을 때의 거래 비용중, 후자가 더욱 중요하다는 것을 알 수 있다. 이 경우 type1을 조금 희생해도 type2 에러를 줄이기 위해 노력할 수 있다.
보통 type1이 늘어나면 type2가 줄어드는 서로 교환 관계에 있는데, 데이터의 수를 늘리면 type1과 type2가 함께 줄어드는 경향이 있다. 물론 대신 처리 비용이 늘어난다.
TNR(true negative rate) = 1-FPR
: 내가 안전하다고 생각했을 때 실제로 안전해야 되는 상황, 예를 들어 의약품의 안전성 테스트에서 중요한 지표.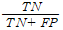
NPV(negative predictive value) = 1-FNR
: 예를 들어, 어떤 검사에서 이상이 없다고 나왔을 때 다시 한번 검사하는 비용이 크다면, 이 비율을 높이고 싶음.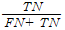
FDR(false discovery rate)
: 내가 참이라고 생각했는데 틀렸을 확률: 맞다고 결정을 내렸는데 틀렸을 때의 비용이 큰 경우
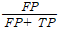
TPR(true positive rate = recall): 1-FNR
: FNR와 마찬가지로 비용을 감수하고 거짓 거래를 잡는 사례 등.
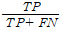
PPV(positive predictive value = precision)=1-fpr
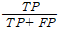
F beta score
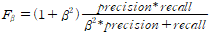
beta는 내가 정하는 값으로, beta가 1이면 F1 score이다. 이때는 precision과 recall의 조화평균이 된다. recall가 중요할수록 큰 beta값을 사용한다.
F1 score는 거의 모든 분류 문제에서 사용하는 지표 중 하나다.
MCC(Matthews Correlation Coefficient)
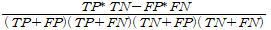
예측된 class와 실제와의 상관관계를 나타내는 값. y_true와 y_pred사이의 corr을 구해도 같다고 한다. 불균형한 문제를 다루고 있거나, 쉽게 해석하려 한다면 사용한다고 한다.
ROC곡선
TPR을 FPR에 대해 플롯팅한 것. TPR이 높고 FPR이 낮은 것이 당연히 더 좋다.
가장 좋은 형태의 그래프 예.
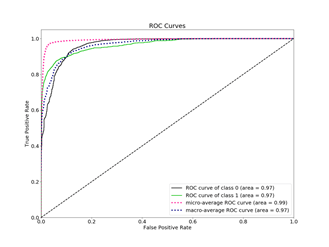
가운데의 직선은 랜덤한 예측에 대한 결과. 적어도 이것보다는 좋아야 됨.
ROC AUC score
ROC곡선이 얼마나 좋은지에 대한 단일 숫자값. ROC아래의 넓이를 계산하면 그게 이 점수가 된다. 이 넓이는 사실 예측과 target의 rank correlation을 계산한 것과도 같다고 한다. 따라서 내 모델이 ranking 예측에 얼마나 좋은지를 보여주는 지표이라는 뜻도 된다.
몇가지 특기점이 있다.
- 내가 랭킹 예측에 신경을 쓸 때는 반드시 사용해야 되는 값이다.
- 데이터가 크게 밸런스가 안 맞을 때는 쓰면 안된다고 한다. FPR이 너무 많은 TN 때문에 값이 자동으로 작아지게 된다고 한다.
- 양 및 음의 class를 모두 신경쓰는 경우에 사용해야 된다.
Precision-Recall Curve
precision 및 recall의 결합을 보여주는 플롯. 모든 임계값마다 두 값을 계산해서 플롯팅한다. 마찬가지로 같은 값에서 y축의 값이 높을수록 성능이 좋다.
어느 시점에서 precision이 급격하게 떨어지는지를 볼 수 있는 기준점을 확인할 수 있다.
PR curve도 PR AUC score가 있다. 이 점수는, 사용하는 각 임계점에 대해 계산한 precision socre의 평균으로 생각할 수 있다.
사용하는 상황은
- 다른 사람들과 precision/recall 결정에 대한 논의가 필요할 때
- 비즈니스 문제를 해결할 때 사용할 임계값을 고를 때
- 데이터가 ‘매우’ 불균현할 때. ppv, tpr모두 positive class에만 신경을 많이 쓰고, negative class에는 별로 신경을 쓰지 않는다.
- possitive이 negative측면보다 중요할 때.
Log loss
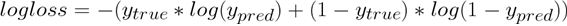
이때 y 값들은 확률.
단, log loss보다 항상 훨씬 더 잘 맞는 metric들이 있다. 별로라고 함.
Brier score
brierloss = 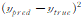
사실 공식은 mean squared error.
cumulative gains chart
내 모델이 랜덤 모델보다 얼마나 잘 맞추는지 gain을 게이지화.
이런 식이다.
