브루트포스 : 순열
임의의 수열을 다른 순서로 섞는 연산
그래서 순서가 매우 중요한 의미를 가지고 있을때 사용한다.(123 != 132)
총 N!개가 존재하고 모든 순서를 다 시도해봐야 할때.
숫자의 나열이 입력으로 들어오면 사용하는 경우가 많음
11! 이하인 브루트 포스에서 숫자 나열인 문제 풀때 사용
브루트포스 문제중에서 순열문제는 결코 그냥 푸는 문제가 아님
문제의 핵심 키워드는
do{
}while(next_permutation(d));
혹은
do{
}while(prev_permutation(d));을 얼마나 요긴하게 사용하는가 이다. 문제는 위와 같은 함수는 오직 cpp에만 정의되어 있기 때문에 문제를 풀거라면 반드시 cpp로 풀고 python이나 java로 푼다고 하면 위의 기능들을 따로 정의해 두어야 한다.
키워드
우선 그냥 브루트 포스를 하더라도 시간이 오래걸린다.
문제
10819 차이를 최대로
그냥 계속 돌려가면서 차이를 최대로 만들면 된다.
대표적인 순열문제로 숫자의 나열, 모든 경우를 할 수 있는 제한이 8!이기에 쌉가능
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i,j,n;
int main(void) {
//freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
vector<int> a(n);
for (i = 0; i < n; ++i) {
cin >> a[i];
}
sort(a.begin(), a.end());
do {
int temp = 0;
for (i = 0; i < n-1; i++) {
if (n%2==1 && i == n - 1) {
temp += a[i];
}
else {
temp += abs(a[i] - a[i + 1]);
}
}
ans = max(ans, temp);
} while (next_permutation(a.begin(), a.end()));
cout << ans << '\n';
}10971 외판원 순회 2
위쪽은 입력을 바꾼다면 여기는 선택하는 걸 바꾼다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i,j,n;
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
vector<vector<int>> a(n, vector<int>(n));
for (i = 0; i < n; ++i) {
for (j = 0; j < n; ++j) {
cin >> a[i][j];
}
}
vector<int> v(n);
for (i = 0; i < n; ++i) v[i] = i;
ans = 1e9;
do {
int minVal = 0;
bool ok = true;
for (i = 0; i < n-1; ++i) {
if (a[v[i]][v[i + 1]] == 0) {
ok = false;
break;
}
else {
minVal += a[v[i]][v[i + 1]];
}
}
if (ok && a[v[i]][v[0]] != 0) {
minVal += a[v[i]][v[0]];
ans = min(ans, minVal);
}
} while (next_permutation(v.begin()+1, v.end()));
cout << ans;
}브루트 포스 : 재귀
문제의 구성
선택 : 어떤 걸 선택해야 할지 모를때 일단 다 선택하는 것
백트래킹 : 선택으로 모든 경우를 다 구하긴 했는데 조건을 만족하기 어려울때 해당 경우를 포기
선택
문제
9095 1,2,3 더하기
이 문제는 물론 DP로 푸는게 보다 낫지만 여기에서는 재귀를 이용해서 문제를 풀어보자
go(sum,goal) : 합 sum을 만드는 경우의 수
1. 불가능한 경우 sum>goal
2. 정답을 찾은 경우 sum==goal
3. 다음 경우 호출 go(sum+i,goal)
1759 암호 만들기
L개의 알파벳 소문자들로 구성되며 최소 한 개의 모음과 최소 두 개의 자음으로 암호를 구성하고 암호를 이루는 알파벳이 암호에서 증가하는 순서로 배열되어야 한다.
암호로 사용할 수 있는 문자의 종류는 C가지
가능성 있는 암호를 모두 구하는 문제이다.
- 사용가능한 알파벳을 정렬한다.
- 각 알파벳이 포함될지 않되지를 모두 결정하면 된다.
그러면 2^C가 시간복잡도가 될 것이다.
go(n,alpha,password,i)
n : 만들어야 하는 암호의 길이
alpha : 사용할 수 있는 알파벳
password : 현재까지 만든 암호
i : 사용할지 말지 결정해야 하는 알파벳의 인덱스
- 정답을 찾은 경우 : password의 길이가 n과 같은 경우, 만들어진 password가 최소 한개의 모음과 두개의 자음으로 구성되었는 지 확인하는 방법이 존재한다.
- 불가능한 경우 : i>=alpha의 사용할 수 있는 문자가 남지 않은 경우
- 다음의 경우 : i번째를 사용하는 경우 go(n,alpha,password+alpha[i],i+1)
i번째를 사용하지 않는 경우 go(n,alpha,password,i+1)
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
l,c=map(int,input().split())
a=list(input().split())
ans=[]
a.sort()
def check(alpha):
even=0
odd=0
for i in alpha:
if(i in 'aeiou'): odd+=1
else: even+=1
return odd>=1 and even>=2
def go(index,alpha,l,c):
if(len(alpha)==l):
if(check(alpha)):
ans.append(alpha)
return
if(index>=c): return
go(index+1,alpha+a[index],l,c)
go(index+1,alpha,l,c)
go(0,"",l,c)
print('\n'.join(ans))14501 퇴사
제한이 15 밖에 안되기 때문에 2^15의 경우만 존재한다.
go(day,sum)의 함수를 사용한다.
day일이 되었을때 day일에 있는 상담을 할지 말지 결정해야 한다.
지금까지 얻은 수익은 sum이다.
- 정답을 찾은 경우 day==N+1, 최댓값 비교
- 불가능한 경우 날짜가 N+1 초과가 된 경우 day > N+1
- 다음의 경우 : 상담을 하는 경우 go(day+T[day],sum+P[day])
상담을 하지 않은 경우 go(day+1,sum)
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t=int(input())
a=list(list(map(int,input().split())) for _ in range(t))
ans=0
def go(sum,day):
global ans
if(day==t):
ans=max(ans,sum)
return
if(day>t): return
go(sum+a[day][1],day+a[day][0])
go(sum,day+1)
go(0,0)
print(ans)백트래킹
재귀 함수를 이용해 브루트 포스를 하다 보면, 더 이상 함수 호출이 의미 없는 경우가 있다. 이 떄, 이런 경우를 제외하고 브루트 포스를 진행하면 백트래킹이라고 한다.
브루트포스는 이게 가능한지 안한지 상관없이 일단 모든 방법을 만들어 보고 나서 아니지 맞는지 결정한다면
백트래킹은 함수의 호출이 진행되던 중에 이게 아무리봐도 더 이상 정답을 구할 수 없다고 생각되는 순간이 오면 함수의 호출을 중단시키는 방법이다.
그냥 재귀와의 코드의 차이는 크지 않지만 시간 차이는 큰편 그래서
문제
14889 스타트와 링크
N명을 N/2명씩 두 팀으로 나누고 두 팀의 능력치를 구한 다음 차이의 최소값을 구하는 문제이다.
S[i][j]=i번째 사람과 j번째 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치
제한이 N=20까지이기 때문에 빅오는 O(2^20)이다.
2^26까지가 1억 미만이다.
- 정답을 찾은 경우 index==n
- 불가능한 경우 : index==n이지만 first와 second의 크기가 n/2가 아닌 경우
- 다음의 경우
1번팀 선택 : go(index+1,first+index,second), go(index+1,first,second+index)
개선 방법 - 백트래킹 사용
예를 들어서 first 팀이 절반이상의 팀을 이미 가지고 있는 경우 더 이상의 호출이 아무런 의미가 없어지게 된다.
- 불가능한 경우 : first와 second의 크기가 n/2가 아닌 경우 return
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n=int(input())
a=list(list(map(int,input().split())) for _ in range(n))
def go(first,second,index):
if(index==n):
if(len(first)!=n//2): return -1
if(len(second)!=n//2): return -1
d1=0; d2=0
for i in range(n//2):
for j in range(n//2):
if(i==j): continue
d1+=a[first[i]][first[j]]
d2+=a[second[i]][second[j]]
diff=abs(d1-d2)
return diff
if(len(first)>n//2 or len(second)>n//2): return -1
ans=-1
t1=go(first+[index],second,index+1)
if(ans==-1 or (t1!=-1 and ans > t1)):
ans=t1
t2=go(first,second+[index],index+1)
if(ans==-1 or (t2!=-1 and ans > t2)):
ans=t2
return ans
print(go([],[],0))15661 링크와 스타트
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n=int(input())
a=list(list(map(int,input().split())) for _ in range(n))
def go(first,second,index):
if(index==n):
if(len(first)==0): return -1
if(len(second)==0): return -1
d1=0; d2=0
for i in first:
for j in first:
if(i==j): continue
d1+=a[i][j]
for i in second:
for j in second:
if(i==j): continue
d2+=a[i][j]
diff=abs(d1-d2)
return diff
if(len(first)==n or len(second)==n): return -1
ans=-1
t1=go(first+[index],second,index+1)
if(ans==-1 or (t1!=-1 and ans > t1)):
ans=t1
t2=go(first,second+[index],index+1)
if(ans==-1 or (t2!=-1 and ans > t2)):
ans=t2
return ans
print(go([],[],0))6603 로또
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
def go(index,ans,a,k):
if(len(ans)==6):
print(' '.join(map(str,ans)))
return
if(index>=k): return
go(index+1,ans+[a[index]],a,k)
go(index+1,ans,a,k)
a=list(map(int,input().split()))
while(a[0]!=0):
go(0,[],a[1::],a[0])
a=list(map(int,input().split()))
print()2529 부등호
부등호 기호 <와 >가 나열된 수열 A가 있다. 기호의 앞 뒤에 한 자리 숫자를 넣어서 모든 부등호 관계를 만족시키려고 한다. k+1개 자리의 정수 중에서 최댓값과 최솟값을 구하는 문제이다.
- 정답을 찾은 경우 : index==n+1
- 불가능한 경우 : check[i]!=1, good(num[index-1],i,a[index-1])
- 다음의 경우 : go(index+1,num+string(i))
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n=int(input())
a=list(input().split())
c=[False]*(10)
ans=[]
def good(pVal,cVal,com):
if(com=='<'): return pVal < cVal
else : return pVal > cVal
def go(i,num,n):
if(len(num)==n+1):
for i in range(1,len(num)):
if(not good(num[i-1],num[i],str(a[i-1]))): return
ans.append(num)
return
for i in range(10):
if(c[i]): continue
c[i]=True
go(i+1,num+str(i),n)
c[i]=False
go(0,"",n)
ans.sort()
print(ans[-1])
print(ans[0])그냥풀면 위와 같이 나타낼 수 있지만 이렇게하면 너무 시간이 오래걸린다.

그래서 선택할때마다 검사하는 방식으로 진행해야 한다.
good(num[index-1],i,a[index-1]) 로 이전의 숫자, 선택한 수, 부등호를 고려해서 넣을 수 없는 수이면 스킵한다.
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n=int(input())
a=list(input().split())
c=[False]*(10)
ans=[]
def good(pVal,cVal,com):
if(com=='<'): return pVal < cVal
else : return pVal > cVal
def go(index,num,n):
if(len(num)==n+1):
ans.append(num)
return
for i in range(10):
if(c[i]): continue
if(index == 0 or good(num[index-1],str(i),str(a[index-1]))):
c[i]=True
go(index+1,num+str(i),n)
c[i]=False
go(0,"",n)
ans.sort()
print(ans[-1])
print(ans[0])
1248 맞춰봐
-10부터 10까지 N개의 정수(중복 X)로 이루어진 수열 A가 있다.
S[i][j]=A[i]+A[i+1]+...+a[j] 가 0보다 크면 +, 작으면 -, 같으면 0이다.
S가 주어졌을 때 가능한 A를 아무거나 찾는 문제
일단 그냥 풀어보고 어떻게하면 시간을 줄일 수 있으지 생각해보자
총 21개의 수를 10개의 자리에 넣을 수 있다. 그래서 21^10의 엄청난 경우의 수가 나온다.
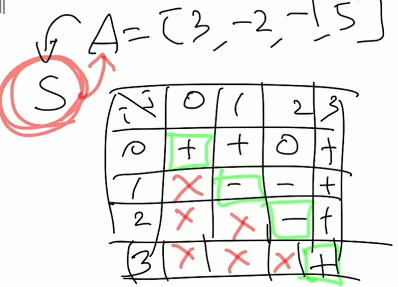
그렇기에 여기에서 눈 여겨봐야 하는 부분은 i==j인 경우이다. i==j가 +이면 i번째 숫자는 양수라는 것을 알 수 있고 -이면 음수라는 것을 알 수 있다.
이번에는 i,i 에서의 숫자의 부등호를 찾았으니 i,i+1와 같이 대각선이 아닌 부분을 값을 삽입할때마다 검사를 해주는 것이다.
