알고리즘 캠프
개념
완전탐색 : 가능한 경우의 수를 모두 조사하는 방법
컴퓨터는 1억(10^8)=1초 이기 때문에 컴퓨터에게 있어서 부르트 포스는 어렵지 않다.
문제
2231 분해합
숫자를 가지고 각자리의 합이 원하는 값이 나오면 된다.
여기에서 제한이 1,000,000 밖에 되지 않기 때문에 1부터 시작해서 값 이전까지 구하면 된다.
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t=int(input())
ans=0
flag=True
for i in range(1,t):
ans=i
temp=str(i)
for j in range(len(temp)):
ans+=int(temp[j])
if(ans==t):
print(i)
flag=False
break
if(flag):print(0)1018 체스판 다시 칠하기
지민이가 mxn 판을 가지고 와서 8x8 의 검흰이 반복되는 체스판을 만드는 문제이다.
나올수 있는 경우가 (M-7)x(N-7) 정도 될것이다. 하지만 제한이 50이다. 여기에 추가로 8x8 칸을 모두 확인할 테니 50x50x8x8=160,000 경우밖에 없다.
조금 더 빠르게 검사하는 방법
Case 1: 모든 B 짝수이면 모든 W 홀수
Case 2: 모든 B 홀수이면 모든 W 짝수
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n,m=map(int,input().split())
a=list(list(map(str,input().rstrip())) for _ in range(n))
ans=1e9
for i in range(n-7):
for j in range(m-7):
# num1은 정상적인 것
# num2는 수정해야 하는 것
num1=0
num2=0
for k in range(i,i+8):
for l in range(j,j+8):
if(a[k][l]=='W'):
if((k+l)%2==0): num1+=1
else: num2+=1
else:
if((k+l)%2==0): num2+=1
else: num1+=1
ans=min(ans,num1,num2)
print(ans)15649 N과 M(1)
브루트포스 재귀의 대표적인 유형
8가지 수를 8칸에 넣는 것이기에 8^8<10^8 의 문제이다.
그냥 for문을 8중으로 중첩시키어야 하는데 당연컨데 풀 수가 없다. 그래서 이렇게 for문이 과하게 중첩되거나 가변적이면 재귀를 이용하는 방법이 있다.
재귀함수란? 어떤 함수에서 자기 자신을 호출하는 함수를 지칭한다.
반드시 기조코드를(반환코드) 잘 세우자
백트래킹 : 현재 상태에서 가능한 후보군으로 가지를 치며 탐색하는 알고리즘
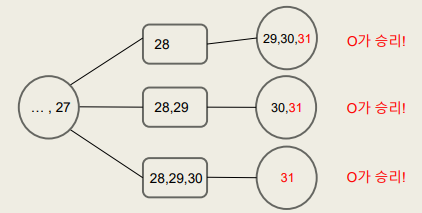
위와 같이 할 수 있는 경우로 가지를 치는 알고리즘이다.
변수로는 인덱스,입력값들 + 확인 배열,정답 배열
import sys,heapq
#sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n,m=map(int,input().split())
a=[0]*(m)
check=[False]*(n+1)
def go(index,n,m):
if(index==m):
print(' '.join(map(str,a)))
return
for i in range(1,n+1):
if(check[i]): continue
check[i]=True
a[index]=i
go(index+1,n,m)
check[i]=False
go(0,n,m)15650 N과 M(2)
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n,m=map(int,input().split())
a=[0]*(m)
check=[False]*(n+1)
def go(index,select,n,m):
if(index==m):
print(' '.join(map(str,a)))
return
for i in range(select,n+1):
if(check[i]): continue
check[i]=True
a[index]=i
go(index+1,i,n,m)
check[i]=False
go(0,1,n,m)9663 N-Queen
내가 알기로는 이건 DFS 문제이다.
필수적인 것은 같은 (/)대각선에 위치한 것의 행과 열의 합은 동일하다.
() 행과 열을 뺀것과 동일하다.
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n=int(input())
ans=0
c=[0]*n
def check(index):
for i in range(index):
if(c[i]==c[index] or abs(c[i]-c[index])==index-i):
return False
return True
def go(index,n):
global ans
if(index==n):
ans+=1
return
for i in range(n):
c[index]=i
if(check(index)):
go(index+1,n)
go(0,n)
print(ans)#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i,n;
int c[16];
bool check(int index) {
for (int i = 0; i < index; ++i) {
if (c[i] == c[index] || abs(c[i] - c[index]) == (index - i)) return false;
}
return true;
}
void go(int index){
if (index == n) {
ans += 1;
return;
}
for (int i = 0; i < n; ++i) {
c[index] = i;
if (check(index)) {
go(index + 1);
}
}
}
int main(void) {
freopen("input.txt", "r", stdin);
cin >> n;
go(0);
printf("%d",ans);
}브루트 포스-기본
개념
모든 경우를 다 시도해 보는 알고리즘
모든 문제를 풀 수 있는 알고리즘이 아닌 경우의 수가 정해져 있는 문제를 풀 수 있는 알고리즘
대략 1억개 = 1초 걸린다고 생각하면 된다.
기본 메커니즘
- 방법의 수-시간 복잡도를 계산한다. O(경우의 수 * 방법 1개를 시도하는데 걸리는 시간)
- 가능한 모든 방법을 다 만들어 본다.
- 실재로 각 방법을 이용해 답을 구한다.
for문 중첩을 이용하여서 문제를 풀어준다.
방법의 수 = 경우의 수

1번 : N (N-1) ... = N!
2번 : nC2
3번 : nC3
4번 : nC1 * n-1C1
5번 : 2^n
문제
2309 일곱 난쟁이
가장 기본적인 문제이며 그냥 답이 나오면 중간에 멈추고 결과들을 출력하면 된다.
아홉명 중에 7명이기 때문에 경우의 수가 9C2 이다. 그렇기 때문에 for문 중첩으로 풀면 된다.
import sys
sys.stdin = open("input.txt","r")
a=[int(input()) for _ in range(9)]
ans=sum(a)
a.sort()
for i in range(0,9):
for j in range(i+1,9):
if(ans-a[i]-a[j]==100):
for k in range(9):
if(k!=i and k!=j):
print(a[k])
sys.exit(0)3085 사탕 게임
보드가 50x50이 최대이다.
탐색을 하는 시간 : O(n^2)
바꾸는 시간 : O(2 * n^2) 오른쪽, 아래로만 바꾼다고 가정
총 시간 : O(12,500,000)
문제 제한은 1초이기 때문에 이 안에 풀 수 있다.
import sys
sys.stdin = open("input.txt","r")
def check(a):
n = len(a)
c =1
ans = 1
for i in range(n):
# 행검사
c=1
for j in range(1,n):
if(a[i][j]==a[i][j-1]): c+=1
else: c=1
if(ans<c): ans=c
c=1
for j in range(1,n):
if(a[j][i]==a[j-1][i]): c+=1
else: c=1
if(ans<c): ans=c
return ans
n = int(input())
a = [list(input()) for i in range(n)]
ans = 0
for i in range(n):
for j in range(n):
# 가로
if(j+1<n):
a[i][j],a[i][j+1] = a[i][j+1],a[i][j]
tmp = check(a)
if tmp>ans : ans = tmp
a[i][j],a[i][j+1] = a[i][j+1],a[i][j]
# 아래
if(i+1<n):
a[i][j],a[i+1][j]=a[i+1][j],a[i][j]
tmp = check(a)
if tmp>ans : ans=tmp
a[i][j],a[i+1][j]=a[i+1][j],a[i][j]
print(ans)문제를 푸는 데 swap과 check 두개의 함수가 C++에서는 필요하다. 하지만 python에서의 값을 바꾸는 것은 매우 강력한 기능이 있기 때문에 이 부분을 단순한 연산으로 해결할 수 있었다.
방법2
1476 날짜계산
- 문제설명

광활한 우주~ 황야와 같은 우주 안에서 그저 모래 한톨에 불과한 인간의 존재~ 인간은 과연 어떤 목적을 위하여 존재하는 걸까요?
이런 처락적인 질문을 답하기 전에 다른 우주에 있는 우리 준규 행성의 나이를 계산해 보자
문제의 범위 : O(15 * 28 * 19)
그냥 카운트만 계속 올리면서 사용자가 요청한 값이 나오게 하면 된다.
import sys
sys.stdin = open("input.txt","r")
e,s,m=map(int,input().split())
e-=1
s-=1
m-=1
c=0
while(True):
if(c%15 == e and c%28 == s and c%19 ==m):
print(c+1)
break
c+=1중국인의 나머지 정리
1107 리모컨
최악의 경우 누를 수 있는 모든 버튼을 누른 다음 +또는 -를 수행하여야 한다.
그렇기 때문에 최대 50만까지 버튼이 있고 모든 버튼을 눌러보면서 연산을 수행한다고 생각해보면 최악의 경우 100만 정도의 경우의 수가 나오게된다.
여기에서 좋은 팁은 python은 abs라는 것이 따로 존재하여서 ans = n-100 할때 음수가 나올 걱정을 덜 수 있다.
여기에서 중요한 것은 브루트포스 문제가 최솟값을 구하는 문제라는 점이다. 최소를 구할때는 반드시 의미없는 것이 있어서는 안되며 중복되는 것도 있어서는 안된다.
import sys
sys.stdin = open("input.txt","r")
n = int(input())
b = int(input())
broken = [False]*10
if(b>0):
tmp = list(map(int,input().split()))
for i in tmp:
broken[i]=True
def check(i):
##global broken
if(i==0): return 0 if(broken[int(i)]) else 1
len = 0
while(i>0):
if(broken[int(i%10)]): return 0
len+=1
i//=10
return len
ans=abs(n-100)
sum=-1
for i in range(0,1000000):
len = check(i)
if(len>0):
tmp = abs(n-i)
if(ans>len+tmp): ans = len+tmp
print(ans)14500 테트로미노
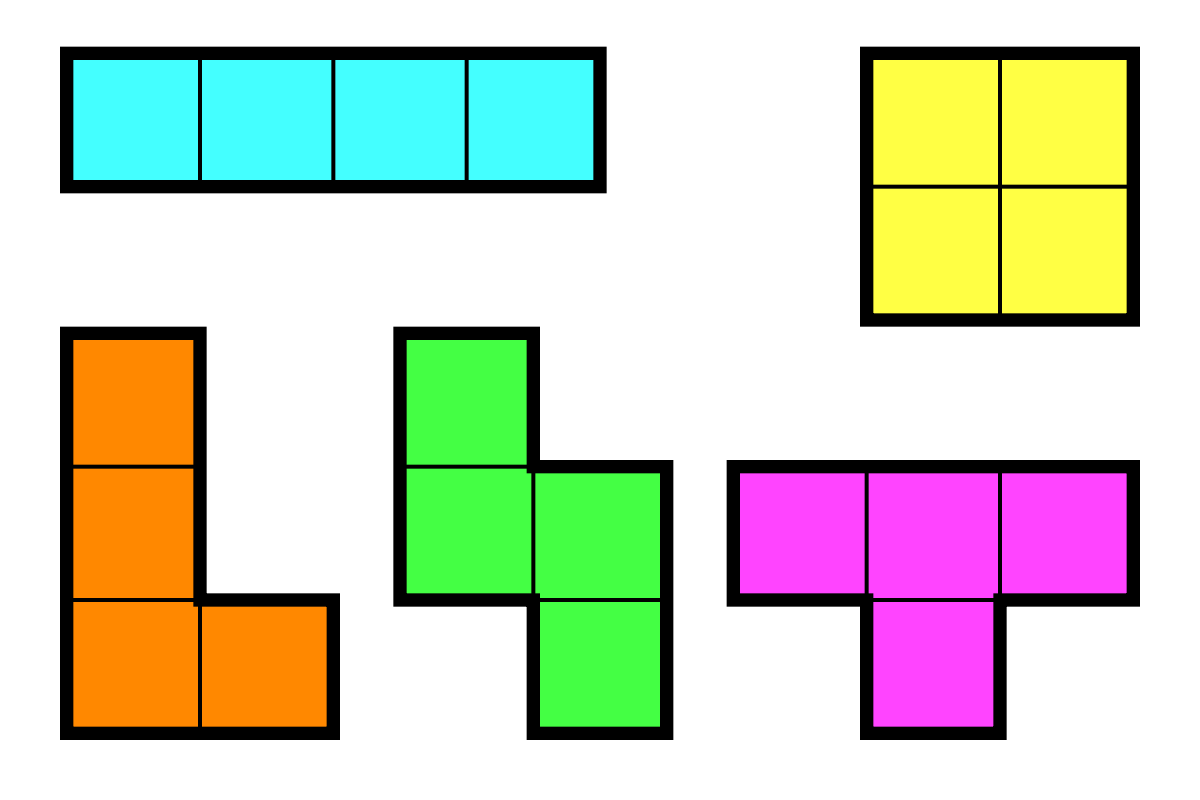
1x1 정사각형 4개로 만든 모형들 : 총 5개만 존재
종이의 크기가 500x500 정도이다. 여기에 티트로미노 딱 하나만을 놓아서 종이위에 적힌 점수를 최대로 얻어갈 수 있는 방법을 구하는 문제이다.
별거 없다. 그냥 블록 하나 정해서 계속 뗏다 붙였다 하면 된다.
이때 나올수 있는 경우는 19가지이고
250000x19 = 4,750,000 가지의 방법의 수가 나오기 때문에 충분히 돌릴만 하다.
n,m = map(int,input().split())
a = [list(map(int,input().split())) for _ in range(n)]
ans = 0
for i in range(n):
for j in range(m):
if j+3 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i][j+3]
if ans < temp: ans = temp
if i+3 < n:
temp = a[i][j] + a[i+1][j] + a[i+2][j] + a[i+3][j]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i+1][j] + a[i+1][j+1] + a[i+1][j+2]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j] + a[i+2][j]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i+1][j+2]
if ans < temp: ans = temp
if i+2 < n and j-1 >= 0:
temp = a[i][j] + a[i+1][j] + a[i+2][j] + a[i+2][j-1]
if ans < temp: ans = temp
if i-1 >= 0 and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i-1][j+2]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i+1][j] + a[i+2][j] + a[i+2][j+1]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i+1][j]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j+1] + a[i+2][j+1]
if ans < temp: ans = temp
if i+1 < n and j+1 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j] + a[i+1][j+1]
if ans < temp: ans = temp
if i-1 >= 0 and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i-1][j+1] + a[i-1][j+2]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i+1][j] + a[i+1][j+1] + a[i+2][j+1]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j+1] + a[i+1][j+2]
if ans < temp: ans = temp
if i+2 < n and j-1 >= 0:
temp = a[i][j] + a[i+1][j] + a[i+1][j-1] + a[i+2][j-1]
if ans < temp: ans = temp
if j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2]
if i-1 >= 0:
temp2 = temp + a[i-1][j+1]
if ans < temp2: ans = temp2
if i+1 < n:
temp2 = temp + a[i+1][j+1]
if ans < temp2: ans = temp2
if i+2 < n:
temp = a[i][j] + a[i+1][j] + a[i+2][j]
if j+1 < m:
temp2 = temp + a[i+1][j+1]
if ans < temp2: ans = temp2
if j-1 >= 0:
temp2 = temp + a[i+1][j-1]
if ans < temp2: ans = temp2
print(ans)
브루트 포스 - 기본 : 건너뛰며 풀기
개념
기본 브루트 포스 형태로 문제를 풀 수 있지만 그냥 풀면 시간제한을 넘기기 때문에 특정 경우를 건니뛰면서 푸는 방식이다. 자주 나오는 건 아니지만 알아두면 좋다.
메커니즘
브루트 포스인데 경우의 수가 너무 많다.
1. 모든 경우를 작성하기
2. 작성하면서 규칙 찾아내기
문제
6064 카잉 달력
문제는 앞에서 보았던 날짜계산하고 비슷해 보인다. 문제는 경우의 수가 넘사다... 1,600,000,000 가지의 경우의 수가 존재한다. 미친...
그래서 건너뛰기를 하여야 한다.
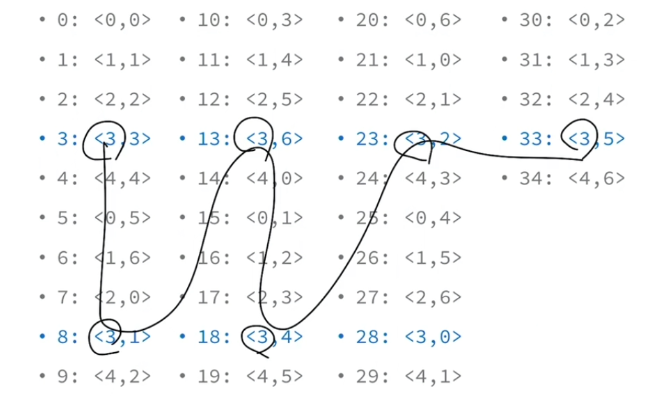
여기에서 알 수 있는 것은 x값은 M값만큼 증가할때 마다 같다라는 거다.(어찌보면 당연하다) 반면 y값은 그때마다 값이 달라지기 때문에 x값에 M만큼 계속해서 더해가면서 y값이 우리가 원한 y값이 나올때까지 구하면 된다.
보면 알겠지만 브루트포스 : 건너뛰기는 그냥 기본문제중에서도 시간이 많이 나오는 문제를 규칙을 찾아내서 풀어내는 방식이다.
import sys
sys.stdin = open("input.txt","r")
t = int(input())
for _ in range(t):
m,n,x,y=map(int,input().split())
x-=1
y-=1
ok =False
for k in range(x,n*m,m):
if(k%n==y):
print(k+1)
ok=True
break
if(not ok): print(-1)1748 수 이어 쓰기 1
숫자를 다 이어 붙이면 되는 문제이다. 흠... 문제 제한이 1억이기 때문에 그냥 이어붙이면 시간내에 풀 수가 없다. 그렇기 때문에 1 10 100 단위로 뛰어가면서 그냥 문자의 길이를 더해주기만 하면 문제를 쉽게 풀어낼 수 있다.
이 역시 자릿수대로 뛰어 가면 된다는 규칙을 찾은걸로 볼 수 있다.
import sys
sys.stdin = open("input.txt","r")
n = int(input())
ans = 0
end = 1
c=1
start = 1
while(start<=n):
end = start*10-1
if(end>n): end = n
ans+=(end-start+1)*c
c+=1
start*=10
print(ans)브루트 포스 : 기본 - N중 for문
n개 중에 일부를 선택해야 하는 경우 사용하는 문제
문제
9095-1,2,3 더하기
브루트 포스 : 방법 만들기
브루트 포스에서 방법을 만드는 방법에는 크게 3가지가 존재한다.
1. 재귀 사용(순열과 비트마스크 사용 방법은 재귀로 제작 가능)
-순서문제
-선택문제
2. 순열 사용
3. 비트마스크 사용
브루트 포스 : 방법 만들기 - 재귀
- 재귀 사용(순열과 비트마스크 사용 방법은 재귀로 제작 가능)
-순서문제
-선택문제
재귀 키워드
- 많은 수의 중첩 for문이 필요한 알고리즘일때 사용 (입력 만큼의 for문이 반드시 필요한 경우가 대표적인 경우이다.)
- for문의 범위를 넘는 인덱스를 갔다올 수 있을때 사용
선택 키워드
- 문제 내에 오름차순/내림차순 관련 키워드가 존재한다면 선택문제의 형태로 재귀적으로 풀 수 있다. 자세한건 N과 M(2) 확인하기
알고리즘
- 다음 경우 : 어떻게 풀지를 우선 생각하여 본다.(for문 활용)
- 정답을 찾은 경우 : 그리고 풀어낸 결과를 어떻게 확인할지를 생각해 본다.
- 불가능한 경우(없는 경우도 존재) : 불가능한 경우가 언제인지도 생각하여 본다.
단 3가지 스텝으로 재귀로 브루트포스를 풀 수 있다.
문제
15649 N과 M (1)
1부터 N 까지 자연수 중에서 중복 없이 M개를 고른 수열을 모두 구하는 문제
m 개의 자리에 n까지의 숫자를 넣는 방법을 모두 출력하는 문제이다.
중복을 제거해 주기 위해 c[i]라는 배열을 사용할 것이다. 그리고 값을 다른 곳에 따로 저장해 두어서 순서의 중복역시 일어나지 않게 할 계획이다.
시간복잡도는 O(n!)
import sys
sys.stdin = open("input.txt","r")
n,m=map(int,input().split())
c=[False]*(n+1)
a=[0]*(n+1)
def go(index,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return 0
for i in range(1,n+1):
if(c[i]): continue
c[i]=True
a[index]=i
go(index+1,n,m)
c[i]=False
go(0,n,m)15650 N과 M (2)
결과가 오름차순이어야 한다는 N과 M (1)의 약간 다른 버전이다. 이번에는 오름차순을 구현하기 위해 start이라는 변수를 추가해 준다. 이 start라는 변수를 기준으로 그 다음에 오는 값은 start 보다 1 큰 값이 될 것이다.
- 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열
- 고른 수열은 오름차순이어야 한다. : 선택풀이 가능
import sys
sys.stdin = open("input.txt","r")
n,m=map(int,input().split())
c=[False]*(n+1)
a=[0]*(n+1)
def go(index,start,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return 0
for i in range(start+1,n+1):
if(c[i]): continue
c[i]=True
a[index]=i
go(index+1,i,n,m)
c[i]=False
go(0,0,n,m)여기에서 추가적으로 c배열은 start의 존재로 인하여 딱히 필요가 없다.
import sys
sys.stdin = open("input.txt","r")
n,m=map(int,input().split())
a=[0]*(n+1)
def go(index,start,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return 0
for i in range(start+1,n+1):
a[index]=i
go(index+1,i,n,m)
go(0,0,n,m)이것도 아니면 또 다른 방법이 존재한다. 결국에는 오름차순을 반드시 맞추어야 하기 때문에 숫자를 선택하기만 하면 오름차순으로 만들 수 있는 선택 의 관점에서 문제를 풀 수도 있다. 이때는 O(2^n) 이다.
선택을 표현하기 위해서는 재귀를 이용한 함수의 호출로 이 문제를 해결할 수 있다.
select는 선택한 수의 갯수, index는 현재 넣을지 말지를 고민하고 있는 숫자를 의미한다.
import sys
sys.stdin = open("input.txt","r")
n,m=map(int,input().split())
c=[False]*(n+1)
a=[0]*(n+1)
def go(index,select,n,m):
if(m==select):
for i in range(select):
print(a[i],end=' ')
print()
return 0
if(index>n): return
a[select] = index
go(index+1,select+1,n,m)
a[select] = 0
go(index+1,select,n,m)
go(1,0,n,m)15651 N과 M (3)
이번에는 중복이 허용되는 문제이다. 별거 없다. 그냥 기존에 사용하였는지를 검사하였던 c[] 리스트를 지우기만 하면 된다.
- 1부터 N까지 자연수 중에서 M개를 고른 수열
- 같은 수를 여러 번 골라도 된다. : 중복체크 불필요
import sys
sys.stdin = open("input.txt","r")
n,m=map(int,input().split())
a=[0]*(n+1)
def go(index,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return 0
for i in range(1,n+1):
a[index]=i
go(index+1,n,m)
go(0,n,m)15652 N과 M (4)
중복 허용, 오름차순 문제이다.
import sys
sys.stdin = open("input.txt","r")
n,m=map(int,input().split())
c=[False]*(n+1)
a=[0]*(n+1)
def go(index,start,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return
for i in range(start,n+1):
a[index]=i
go(index+1,i,n,m)
go(0,1,n,m)15654 N과 M (5)
5번부터는 기존과 조금 다르게 진행이 된다. 문제에서 값들이 주어지기 때문에 해당 값들을 미리 저장해놓고 N과 M(1)과 같은 방식으로 출력하면 된다.
import sys
sys.stdin = open("input.txt","r")
n,m = map(int,input().split())
num = list(map(int,input().split()))
c=[False]*10001
a=[0]*(n+1)
num.sort()
def go(index,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return
for i in num:
if(c[i]): continue
c[i]=True
a[index]=i
go(index+1,n,m)
c[i]=False
go(0,n,m)15655 N과 M (6)
별거 없다. 그냥 앞에서 배웠던 start 인자를 그대로 응용하면 쉽게 풀 수 있다.
import sys
sys.stdin = open("input.txt","r")
n,m = map(int,input().split())
num = list(map(int,input().split()))
c=[False]*10001
a=[0]*(n+1)
num.sort()
def go(index,start,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return
for i in range(start,len(num)):
a[index]=num[i]
go(index+1,i+1,n,m)
go(0,0,n,m)15656 N과 M (7)
import sys
sys.stdin = open("input.txt","r")
n,m = map(int,input().split())
num = list(map(int,input().split()))
c=[False]*10001
a=[0]*(n+1)
num.sort()
def go(index,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return
for i in num:
a[index]=i
go(index+1,n,m)
go(0,n,m)15657 N과 M (8)
- N개의 자연수 중에서 M개를 고른 수열
- 같은 수를 여러 번 골라도 된다. : 중복체크를 안해도 된다.
- 고른 수열은 비내림차순이어야 한다.
import sys
sys.stdin = open("input.txt","r")
n,m = map(int,input().split())
num = list(map(int,input().split()))
c=[False]*10001
a=[0]*(n+1)
num.sort()
def go(index,start,n,m):
if(m==index):
for i in range(index):
print(a[i],end=' ')
print()
return
for i in range(start,len(num)):
a[index]=num[i]
go(index+1,i,n,m)
go(0,0,n,m)15657 N과 M (9)
9번부터는 문제가 특이해지는데 우선 중복제거라는 조건이 붙게된다. 이것을 해결하기 위해서 (5)번 방식 + 중복제거로 문제를 풀어야 한다.
이를 위해서 출력할 결과물을 바로 출력하는 게 아닌 우선 한 배열에 저장해 놓은 다음에 중복을 제거한 후 출력하는 방식으로 문제를 풀어야 한다.
c++에서는 unique를 이용하면 되고
python에서는 집합인 set을 이용하면
중복제거를 할 수 있다.
import sys
sys.stdin = open("input.txt","r")
n,m = map(int,input().split())
num = list(map(int,input().split()))
c=[False]*(n+1)
a=[0]*(m)
num.sort()
d=[]
def go(index,n,m):
if(m==index):
temp=[num[a[i]]for i in range(m)]
d.append(tuple(temp))
return
for i in range(n):
if(c[i]): continue
c[i]=True
a[index]=i
go(index+1,n,m)
c[i]=False
go(0,n,m)
d=list(set(d))
d.sort()
for i in d:
print(' '.join(map(str,i)))
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int a[10];
int num[10];
int c[10];
vector<vector<int>> d;
void go(int index, int n, int m) {
if (index == m) {
vector<int> temp;
for (int i=0; i<m; i++) {
temp.push_back(num[a[i]]);
}
d.push_back(temp);
return;
}
for (int i=0; i<n; i++) {
if (c[i]) continue;
c[i] = true;
a[index] = i;
go(index+1, n, m);
c[i] = false;
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i=0; i<n; i++) {
cin >> num[i];
}
sort(num,num+n);
go(0,n,m);
sort(d.begin(), d.end());
d.erase(unique(d.begin(),d.end()),d.end());
for (auto &v : d) {
for (int i=0; i<m; i++) {
cout << v[i];
if (i != m-1) {
cout << ' ';
}
}
cout << '\n';
}
return 0;
}추가문제
9095 1,2,3 더하기
1,2,3 더하기 문제를 재귀로 풀어보자
이를 위해서는 우선 어떻게 코드를 구현할지 생각하여 봐야 한다.
go(count,sum,goal)을 입력받고
sum+i
count+1
로 계속 넘어간다.
케이스는 다음과 같다.
1. sum이 goal을 넘어간 경우
2. 정답을 찾은 경우
3. 그다음 넘어가기 go(count+1,sum+i,goal)
이런식으로 풀면 기존의 dp와 같이 점화식을 세우지 않고 계속해서 케이스에 대비하여 코드를 짜면 문제를 풀 수 있다.
import sys
sys.stdin = open("input.txt","r")
t = int(input())
def go(sum,goal):
if(sum>goal): return 0
if(sum==goal): return 1
ans = 0
for i in range(1,4):
ans+=go(sum+i,goal)
return ans
for i in range(t):
m = int(input())
print(go(0,m))
1759 암호 만들기
15가지 밖에 없기 때문에 시간복잡도에서 있어서 큰 문제가 생기지 않는다. 시간복잡도 : O(2^15)
1. 증가하는 순서로 배열되어 있어야 한다. => 일단 정렬을 이용(N과 M 과 동일)
2. 모음 1개와 자음 2개가 최소로 존재하여야 함 => 이런 조건은 매번 확인해주는 것은 매우 복잡하고 힘든 일이기 때문에 문자열을 만든다음에 검사하는 방식으로 수행
선택문제 의 형태로 문제를 풀면 된다.
-
정답을 찾은 경우
go(n,alpha,password,i)
password의 길이가 n이면 정답을 찾은것으로 취급 -
불가능한 경우
만약 현재 가지고 있는 것이 alpha의 i번째 문자인데 이것을 넘어간 문자라서 길이 n을 넘어가게 된다면 이는 불가능한 경우라고 생각할 수 있다. -
다음 경우
i 번째를 사용 : go(n,alpha,passowrd+alpha[i],i+1)
i 번째를 사용안함 : go(n,alpha,password,i+1)
import sys
sys.stdin = open("input.txt","r")
# a 65 e 69 i 73 o 74 u 75
def check(ans):
vo = 0 #모음
co = 0 #자음
for i in ans:
if i in 'aeiou': vo+=1
else: co+=1
return vo>=1 and co>=2
def go(n,a,ans,i):
if(len(ans) == n):
if check(ans):
print(ans)
return
if(i>=len(a)): return
go(n,a,ans+a[i],i+1)
go(n,a,ans,i+1)
l,c = map(int,input().split())
a = list(input().split())
a.sort()
go(l,a,"",0)14501 퇴사
퇴사 문제는 원래 DP로 점프점프 형태로 푸는 것이 가장 좋은 방법이지만 일단 여기에서는 재귀의 연습을 위해서 재귀로 문제를 풀어보자.
퇴사 문제는 입력의 갯수만큼 for문이 많이 필요하다. 왜냐하면 내가 선택한 날짜에 상담을 할 수도 안할 수도 있기 때문에 이를 선택의 문제 혹은 n개의 중첩 for문 문제로 볼 수 있기 때문이다.
O(2^n)인데 15가 최대 숫자이다. 그러므로 2^15=32768
go(day,sum)
day일이 되었을 때 상담을 할지 말지를 결정, 수익은 sum이다.
- 탈출
day가 n+1이면 탈출 - 불가능한 경우
day>n+1이면 불가능 - 다음 경우
go(day+d[i],sum+p[i]) # 상담을 한 경우
go(day+1,sum) # 상담을 하지 않은 경우
import sys
sys.stdin=open("input.txt","r")
n=int(input())
t=[0]*(n+1)
p=[0]*(n+1)
for i in range(1,n+1):
t[i],p[i]=map(int,input().split())
ans=0
def go(day,sum):
global ans
if day==n+1:
ans=max(ans,sum)
return
if(day>n+1): return
go(day+1,sum)
go(day+t[day],sum+p[day])
go(1,0)
print(ans)브루트 포스 : 재귀 - 백트래킹
재귀 함수를 이용해 브루트 포스를 하다 보면, 더 이상 함수 호출이 의미 없는 경우가 있다. 이 때, 이런 경우를 제외하고 브루트 포스를 진행하면 백트래킹이 된다.
키워드
재귀로 문제를 푸는데 예외적인 경우가 문제별로 존재
그 예외적인 경우를 처리해 주어서 문제를 푸는 방식
문제
14889 스타트와 링크
N명을 N/2명의 팀 2개로 나누는 것으로 두 팀의 능력치의 차이가 최소값이 되도록하는 것
1번 사람부터 N번 사람까지 1또는 2번 팀을 선택해서 고르기 때문에
O(2^n)=O(2^20) 이기 때문에 문제를 충분히 풀 수 있다.
- 탈출
index번째 사람이 결정한 경우 index==n - 불가능한 경우
- 다음 경우
1번팀 go(index,first,second)
2번팀 go(index,first,second)
import sys
sys.stdin=open("input.txt","r")
def go(index,first,second):
if(index==n):
if len(first) !=n//2: return -1
if len(second) !=n//2: return -1
t1=0
t2=0
for i in range(n//2):
for j in range(n//2):
if(i==j): continue
t1+=p[first[i]][first[j]]
t2+=p[second[i]][second[j]]
diff=abs(t1-t2)
return diff
if len(first)>n//2 : return -1
if len(second)>n//2 : return -1
ans = -1
t1=go(index+1,first+[index],second)
if(ans==-1 or (t1!=-1 and ans>t1)):
ans=t1
t2=go(index+1,first,second+[index])
if(ans==-1 or (t2!=-1 and t2<ans)):
ans=t2
return ans
n=int(input())
p=[list(map(int,input().split())) for _ in range(n)]
print(go(0,[],[]))15661 링크와 스타트
하지만 위의 경우는 너무 모든 경우를 다 계산한다. 거기에다가 홀수인 경우에 대해 대처를 할 수 없다. 이런건 백트래킹이라고 부를 수 없다.
만약 팀을 고르는데
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 1 | 1 |
위와 같이 구성되었다면 6번부터는 무조건 2번팀을 선택하여야만 한다.
그래서 불가능한 경우
first>n/2
second>n/2
인 경우 first혹은 second에 사람을 넣는 것을 멈추어야 한다.
import sys
sys.stdin=open("input.txt","r")
def go(index,first,second):
if(index==n):
if(len(first)==0): return -1
if(len(second)==0): return -1
t1=0
t2=0
for i in first:
for j in first:
if(i==j): continue
t1+=s[i][j]
for i in second:
for j in second:
if(i==j): continue
t2+=s[i][j]
diff = abs(t1-t2)
return diff
if(len(first)==n): return -1
if(len(second)==n): return -1
ans = -1
t1=go(index+1,first+[index],second)
if(ans==-1 or (t1!=-1 and t1<ans)):
ans=t1
t2=go(index+1,first,second+[index])
if(ans==-1 or (t2!=-1 and t2<ans)):
ans=t2
return ans
n = int(input())
s=[list(map(int,input().split())) for _ in range(n)]
print(go(0,[],[]))2529 부등호
이건 순열 문제이지만 일단 백트래킹으로 문제를 풀어보자 k개의 부등호에 들어갈 k+1개의 숫자를 선택하여서 최댓값과 최솟값을 구하는 문제이다.
각 자리 별로 숫자를 한번씩만 사용할 수 있는데 부등호의 갯수는 9개 뿐이다. 숫자도 0~9까지 10개 이니까 O(10!) = O(3,628,800) 으로 충분히 풀만하다.
그래서 일단 숫자를 만들어 보고 나중에 검사하는 방식으로
- 끝나는 경우
n==index - 예외의 경우
- 그 다음 경우
go(index+1,num+a[index])
하지만 여기에서 생각을 다시 해보면 숫자를 선택하면서 검색하는 것이 조금 더 경우의 수를 줄일 수 있다.
import sys
sys.stdin=open("input.txt","r")
n = int(input())
a=input().split()
check=[False]*10
ans=[]
def good(i,num,con):
if(con=='<'): return i<num
if(con=='>'): return i>num
def go(index,num):
if(index==n+1):
ans.append(num)
return
for i in range(10):
if(check[i]): continue
if(index==0 or good(num[index-1], str(i), a[index-1])):
check[i]=True
go(index+1,num+str(i))
check[i]=False
go(0,'')
ans.sort()
print(ans[-1])
print(ans[0])1248 맞춰봐
i부터 j까지 계산하여 결과가 양수이면 + 음수이면 - 0이면 0을 반환하는 S라는 배열이 존재할때 이거을 만들 수 있게 해주는 A라는 배열을 찾으라는 문제이다.
숫자가 21개이기 때문에 이를 그냥 하면 O(21^10) 가지로 시간내에 풀 수 없다.
여기에서 중요한 것은 i==j 인 경우이다. 이거의 기호에 따라 각 위치별 숫자가 양수인지 음수인지를 확인할 수 있다.
그래서 양수, 음수, 0 인경우가 딱딱 나뉘기 때문에 O(10^10)으로 줄어들었다.
여기에서 한가지 더 만약에 0번째 값이 결정되었다면 0부터 1까지 그리고 1부터 1까지의 값을 계산할 수 있다. 마찬가지로 1번째 값까지 결정되었다면 0번째 부터 2번, 1번째 부터 2번, 2번째 부터 2번 까지의 값을 결정할 수 있다.
브루트포스 : 방법 만들기 - 순열
브루트포스 문제중에서 순열문제는 결코 그냥 푸는 문제가 아님
문제의 핵심 키워드는
do{
}while(next_permutation(d));
혹은
do{
}while(prev_permutation(d));을 얼마나 요긴하게 사용하는가 이다. 문제는 위와 같은 함수는 오직 cpp에만 정의되어 있기 때문에 문제를 풀거라면 반드시 cpp로 풀고 python이나 java로 푼다고 하면 위의 기능들을 따로 정의해 두어야 한다.
키워드
우선 그냥 브루트 포스를 하더라도 시간이 오래걸린다.
알고리즘
문제
25259 부등호
부등호 문제는 대표적인 순열문제를 확인할 수 있는데
우선 그냥 브루트 포스로는 결코 풀리지 않는다는 점이 있다.
왜냐하면 10개의 수 중에서 k+1개를 고르고 (k+1)!만큼 순서를 맞추고 (k+1)만큼 부등호 검사를 하기 때문에 경우의 수가 300억이상의 엄청난 시간복잡도가 나온다.
그러므로 부등호는 고정한 상태로 숫자만 움직이는 순열을 사용해야 한다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <cstdlib>
#include <cstring>
#include <functional>
#define ll long long
#define len 2001
using namespace std;
bool check(vector<int>& d, vector<char>& a) {
for (int i = 0; i < a.size(); ++i) {
if (a[i] == '<' && d[i] > d[i + 1]) return false;
if(a[i] == '>' && d[i] < d[i + 1])return false;
}
return true;
}
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
vector<char> a(t);
for (int i = 0; i < t; i++) {
cin >> a[i];
}
vector<int> small(t+1);
vector<int> big(t+1);
for (int i = 0; i <= t; ++i) {
small[i] = i;
big[i] = 9-i;
}
do {
if (check(small, a)) {
break;
}
} while (next_permutation(small.begin(), small.end()));
do {
if (check(big, a)) {
break;
}
} while (prev_permutation(big.begin(), big.end()));
for (int i = 0; i < big.size(); ++i) {
cout << big[i];
}
cout << '\n';
for (int i = 0; i < small.size(); ++i) {
cout << small[i];
}
}문제
3085 사탕게임
이렇게 2차원 배열 문제를 풀때 반복문은 0부터 조건까지로 잡고
안에 if문으로 특정 케이스를 나누어야 한다. 이렇게 안하고 그냥 0에서 t-1까지만 하면 가장 마지막 행과 열에 있는 성분이 선택되지 않는다.
import sys
sys.stdin=open("input.txt","r")
input = sys.stdin.readline
t=int(input())
a=list(list(input().split('\n')[0]) for _ in range(t))
def check(a):
n = len(a)
c =1
ans = 1
for i in range(n):
# 행검사
c=1
for j in range(1,n):
if(a[i][j]==a[i][j-1]): c+=1
else: c=1
if(ans<c): ans=c
c=1
for j in range(1,n):
if(a[j][i]==a[j-1][i]): c+=1
else: c=1
if(ans<c): ans=c
return ans
ans=0
for i in range(0,t):
for j in range(0,t):
if(j+1<t):
a[i][j],a[i][j+1]=a[i][j+1],a[i][j]
ans=max(check(a),ans)
a[i][j],a[i][j+1]=a[i][j+1],a[i][j]
if(i+1<t):
a[i][j],a[i+1][j]=a[i+1][j],a[i][j]
ans=max(check(a),ans)
a[i][j],a[i+1][j]=a[i+1][j],a[i][j]
print(ans)1476 날짜계산
import sys
sys.stdin=open("input.txt","r")
input = sys.stdin.readline
e,s,m=map(int,input().split())
e-=1
s-=1
m-=1
c=1
while(c%15!=e or c%28!=s or c%19!=m):
c+=1
print(c)그냥 날짜를 계속 카운트하고 e,s,m을 나누는 숫자로 우리가 원하는 값이 나왔는지 확인한다.
여기에서 드모르간의 법칙을 사용해서 while문 조건에 삽입했다.
우리가 찾는 것이
c%15==e and c%28==s and c%19==m 인 경우이니 이것에 not을 붙여서
c%15!=e or c%28!=s or c%19!=m 을 조건으로 삽입했다.
하지만 위와 같이 풀면 시간이 좀 걸린다. 그렇기 때문에 이를 해결하기 위해서 조금 더 넓게 뛰어보자
이를 위해서 우선 15로 나누어 지는 e를 고정하고 15씩 움직이면서 결과를 확인해보자
import sys
sys.stdin=open("input.txt","r")
input = sys.stdin.readline
e,s,m=map(int,input().split())
e-=1
s-=1
m-=1
ran = 15*28*19+1
for i in range(e,ran,15):
if(i%28==s and i%19==m):
print(i+1)
break
하면 위쪽이 계선된 알고리즘이다.
1107 리모컨
n = int(input())
b = int(input())
broken = [False]*10
if(b>0):
tmp = list(map(int,input().split()))
for i in tmp:
broken[i]=True
def check(i):
##global broken
if(i==0): return 0 if(broken[int(i)]) else 1
len = 0
while(i>0):
if(broken[int(i%10)]): return 0
len+=1
i//=10
return len
ans=abs(n-100)
sum=-1
for i in range(0,1000000):
len = check(i)
if(len>0):
tmp = abs(n-i)
if(ans>len+tmp): ans = len+tmp
print(ans)14500 테트로미노
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
n,m=map(int,input().split())
a=list(list(map(int,input().split())) for _ in range(n))
ans = 0
for i in range(n):
for j in range(m):
if j+3 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i][j+3]
if ans < temp: ans = temp
if i+3 < n:
temp = a[i][j] + a[i+1][j] + a[i+2][j] + a[i+3][j]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i+1][j] + a[i+1][j+1] + a[i+1][j+2]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j] + a[i+2][j]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i+1][j+2]
if ans < temp: ans = temp
if i+2 < n and j-1 >= 0:
temp = a[i][j] + a[i+1][j] + a[i+2][j] + a[i+2][j-1]
if ans < temp: ans = temp
if i-1 >= 0 and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i-1][j+2]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i+1][j] + a[i+2][j] + a[i+2][j+1]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2] + a[i+1][j]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j+1] + a[i+2][j+1]
if ans < temp: ans = temp
if i+1 < n and j+1 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j] + a[i+1][j+1]
if ans < temp: ans = temp
if i-1 >= 0 and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i-1][j+1] + a[i-1][j+2]
if ans < temp: ans = temp
if i+2 < n and j+1 < m:
temp = a[i][j] + a[i+1][j] + a[i+1][j+1] + a[i+2][j+1]
if ans < temp: ans = temp
if i+1 < n and j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i+1][j+1] + a[i+1][j+2]
if ans < temp: ans = temp
if i+2 < n and j-1 >= 0:
temp = a[i][j] + a[i+1][j] + a[i+1][j-1] + a[i+2][j-1]
if ans < temp: ans = temp
if j+2 < m:
temp = a[i][j] + a[i][j+1] + a[i][j+2]
if i-1 >= 0:
temp2 = temp + a[i-1][j+1]
if ans < temp2: ans = temp2
if i+1 < n:
temp2 = temp + a[i+1][j+1]
if ans < temp2: ans = temp2
if i+2 < n:
temp = a[i][j] + a[i+1][j] + a[i+2][j]
if j+1 < m:
temp2 = temp + a[i+1][j+1]
if ans < temp2: ans = temp2
if j-1 >= 0:
temp2 = temp + a[i+1][j-1]
if ans < temp2: ans = temp2
print(ans)6064 카잉달력
날짜계산 mk.2
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
for i in range(t):
m,n,x,y=map(int,input().split())
flag = True
x-=1
y-=1
for ans in range(x,m*n+1,m):
if(ans%n==y):
print(ans+1)
flag=False
break
if(flag): print("-1")1748 수 이어 쓰기1
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
mod = 10
ans = 0
c=1
while mod<=t:
ans+=int((mod-mod/10)*c)
c+=1
mod*=10
ans+=int((t-mod/10+1)*c)
print(ans)15649 N과 M(1)
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
n,m=map(int,input().split())
c=[False]*(n+1)
a=[0]*(n+1)
def go(index,n,m):
if(index==m):
for i in range(m):
print(a[i],end=' ')
print()
return
for i in range(1,n+1):
if(c[i]): continue
c[i]=True
a[index]=i
go(index+1,n,m)
c[i]=False
go(0,n,m)15650 N과 M(2)
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
n,m=map(int,input().split())
c=[False]*(n+1)
a=[0]*(n+1)
def go(index,n,m):
if(index==m):
for i in range(m):
print(a[i],end=' ')
print()
return
for i in range(1,n+1):
if(c[i] or (index!=0 and a[index-1]>i)): continue
c[i]=True
a[index]=i
go(index+1,n,m)
c[i]=False
go(0,n,m)10972 다음 순열
import sys
sys.stdin=open("input.txt","r")
input = sys.stdin.readline
def next_permutation(a):
i = len(a)-1
while(i>0 and a[i-1]>=a[i]): i-=1
if(i<=0): return False
j=len(a)-1
while(a[j]<=a[i-1]): j-=1
a[i-1],a[j]=a[j],a[i-1]
j=len(a)-1
while i<j:
a[i],a[j]=a[j],a[i]
i+=1
j-=1
return True
n=int(input())
a=list(map(int,input().split()))
if(next_permutation(a)):
print(' '.join(map(str,a)))
else:
print(-1)10973 이전 순열
import sys
sys.stdin=open("input.txt","r")
input = sys.stdin.readline
def next_permutation(a):
i = len(a)-1
while(i>0 and a[i-1]<=a[i]): i-=1
if(i<=0): return False
j=len(a)-1
while(a[j]>=a[i-1]): j-=1
a[i-1],a[j]=a[j],a[i-1]
j=len(a)-1
while i<j:
a[i],a[j]=a[j],a[i]
i+=1
j-=1
return True
n=int(input())
a=list(map(int,input().split()))
if(next_permutation(a)):
print(' '.join(map(str,a)))
else:
print(-1)10974 모든 순열
import sys
#sys.stdin=open("input.txt","r")
input = sys.stdin.readline
def next_permutation(a):
i = len(a)-1
while(i>0 and a[i-1]>=a[i]): i-=1
if(i<=0): return False
j=len(a)-1
while(a[j]<=a[i-1]): j-=1
a[i-1],a[j]=a[j],a[i-1]
j=len(a)-1
while i<j:
a[i],a[j]=a[j],a[i]
i+=1
j-=1
return True
n=int(input())
a = [i for i in range(1,n+1)]
while(True):
print(' '.join(map(str,a)))
if(not next_permutation(a)): break10819 차이를 최대로
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#define ll long long
#define len 1001
using namespace std;
int main(void) {
freopen("input.txt", "r", stdin);
int t;
scanf("%d", &t);
vector<int> a;
for (int i = 0; i < t; ++i) {
int temp;
scanf("%d ", &temp);
a.push_back(temp);
}
int ans = 0;
sort(a.begin(), a.end());
do {
int c = 0;
for (int i = 0; i < t-1; i += 1) {
c += abs(a[i] - a[i + 1]);
}
ans = max(ans, c);
} while (next_permutation(a.begin(),a.end()));
printf("%d", ans);
}
