그래프
그래프 표현
-
간선 리스트
-
인접 행렬
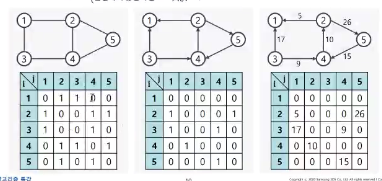
이렇게 2차원 그래프로 표현하는 방식 하지만 이 방식은 많이 사용하지 않음 -
인접 리스트
보다 많이 사용하는 방식
정점의 갯수가 V개, 간선의 개수가 E개인 그래프에 대해서 V개의 연결 리스트로 그래프 정보를 저장
1. 유니온 파인드
상호 배타적 집합
2가지 연산으로 이루어져 있다.
1. Find : x가 어떤 집합에 포함되어 있는지 찾는 연산
2. Union : x와 y가 포함되어 있는 집합을 합치는 연산
구현은 트리를 이용한다.
parent[i]=i의 parent가 저장되어 있음
처음에는 부모가 없으니 자기자신이 부모이다.
Union(1,2)는 뒤에 있는 것을 앞에 있는것에 붙인다.
하지만 이렇게 막 붙일수가 없는게
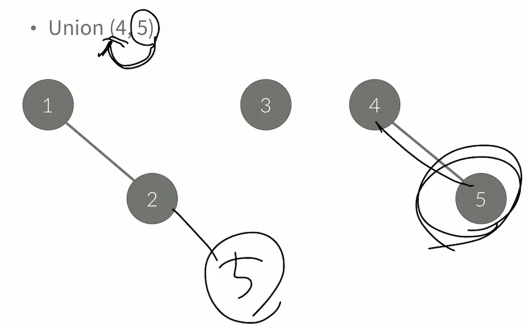
원래 4-5의 관계를 Union(2,5)를 이용해 5만 2에 붙이면 원래는 4개가 하나의 집합이 되어야 하지만 3개만이 하나의 집합이 된다.
그래서 이용하는 것이 find 연산이다. Find 연산은 루트를 찾는 연산이다.

실재로 나온 결과물도 Union(1,4)의 결과물이 된다.
시간 복잡도 : O(n)
int Find(int x){
if(x==parent[x]) return x;
else return Find(parent[x]);
}
시간 복잡도 : O(n)
int Union(int x,int y){
x=Find(x);
y=Find(y);
parent[y]=x;
}하지만 이렇게 하면 사실 O(3N)이기 때문에 비효율적이다. 그래서 사용하는 것이 경로압축이다.
유니온 파인드 : 경로압축
우리에게 중요한것은 루트가 중요하지 부모 자식 관계가 중요한 것이 아니다. 그래서 만난 모든 노드의 부모를 루트로 만들어 주는 것이다.
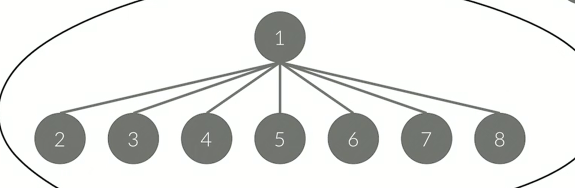
int Find(int x){
if(x==parent[x]) return x;
else {
int y = Find(parent[x]);
parent[x]=y;
return y;
}
}유니온 파인드 : 랭크로 구현
Union을 구현할 때, 트리의 랭크를 기준으로 할 수 있다.
트리의 랭크는 높이와 같은 의미를 갖지만, 경로 압축을 사용하면 높이와 다른 값을 가질 수도 있다. 따라서, 높이 대신 랭크라는 표현을 사용한다.
랭크가 작은 것을 랭크가 높은 것의 자식으로 만든다.
int Union(int x,int y){
x=Find(x);
y=Find(y);
if(x==y) return;
if(rank[x]<rank[y]) swap(x,y);
parent[y]=x;
if(rank[x]==rank[y]){
rank[x]=rank[y]+1;
}
}모든 연산의 시간복잡도 O(a(N))
집합을 나타낼떄 사용
문제
1717 집합의 표현
유니온 파인드 유형 : 정점간의 연결하고 연결되어 있는지 확인하는 유형(집합인지 확인)
부모가 같으면 같은 집합으로 판단
int par[100005];
int find(int a){
if(par[a]==a) return a;
return par[a] = find(par[a]);
}
void merge(int a,int b){
int p_a = find(a);
int p_b = find(b);
par[p_b]=p_a;
}
int main(void){
int n,m,x,y,z;
scanf("%d %d",&n,&m);
for(int i = 1;i<=n;++i){
par[i]=i;
}
for(int i = 0;i<m;++i){
scanf("%d %d %d",&x,&y,&z);
}
}#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i, j,n,m;
int parent[1000001];
int rank_t[1000001];
int Find(int x) {
if (parent[x] == x) {
return x;
}
else {
return parent[x] = Find(parent[x]);
}
}
void Union(int x, int y) {
/* 부모를 찾는 부분 */
x = Find(x);
y = Find(y);
/* 같은 부모이면 스킵 */
if (x == y) return;
/* 랭크가 보다 높은 게 부모가 돰 : 랭크는 연결된 부모의 수를 의미*/
if (rank_t[x] < rank_t[y]) swap(x, y);
parent[y] = x;
/* 부모간 연결, 같은 자식 부모수이면 열결되는쪽 랭크를 증가 */
if (rank_t[x] == rank_t[y]) {
rank_t[x] = rank_t[y] + 1;
}
}
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 0; i <= n; i++) {
parent[i] = i;
rank_t[i] = 0;
}
while (m--) {
int w, x, y;
cin >> w >> x >> y;
if (w == 0) {
Union(x, y);
}
else {
x = Find(x);
y = Find(y);
if (x == y) {
cout << "YES" << '\n';
}
else {
cout << "NO" << '\n';
}
}
}
}2606 바이러스
2. 최소 스패닝 트리(MST)
스패닝 트리중에서 가중치의 합이 가장 작은 트리를 이야기 한다. 모든 정점을 포함하되 가중치가 낮은 간선을 하나만 사용해서 모든 정점을 연결한다.
1) 간선 리스트를 입력 받는다.
2) 간선 리스트를 비용따라 정렬한다.
3) while(true){
간선리스트를 돌면서
if(연결이 안되어 있으면) 두개를 연결한다.
}
4) 연결된 간선의 갯수가 정점갯수-1이면 break;
트리 간선의 갯수 : 정점갯수 -1
그래프를 트리로 만들면 스패닝 트리라고 한다.
스패닝 트리 : 그래프에서 일부 간선을 선택해서 만든 트리
최소 스패닝 트리 : 스패닝 트리 중에 선택한 간선의 가중치의 합이 최소인 트리
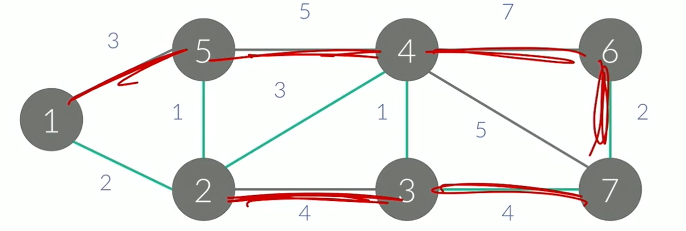
프림과 크루스칼 알고리즘이 존재하는데 중요한 것은 사이클을 만들지 않는 것이다.
프림
아무 정점에서 시작해서 연결된 간선중 최소값을 고르면서 스패닝 트리를 만드는 방식
하나의 정점을 선택하기 위해서는 연결된 모든 간선 중에서 살피어 봐야 하기 때문에
O(V x E) 인데 E의 최댓값은 V^2이기 때문에 O(V^3)이다.
문제
1922 네트워크 연결
이 문제를 풀기위해서 우선순위 큐를 이용하는 방법이 존재한다.
모든 간선은 세가지로 나눌 수 있다. 선택한 정점과 선택하지 않은 정점

그래서 하나를 선택해 버리면 모든 관계는 선-선X, 선-선 형태로 바뀌게 된다. 이때 간선에 대한 정보를 (from, to, cost) 우선순위 큐에 넣어버리면 logE만에 간선을 선택할 수 있게 된다.
그래서 최종 시간 복잡도는 O(ElogE)가 된다.
우선순위 큐에는 (to, cost)만 넣는다. 왜냐하면 from은 이미 선택되어 있기 때문에 의미가 없고 따로 배열을 만들기도 할 것이다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i, j,n,m;
struct Edge {
int to;
int cost;
bool operator < (const Edge& other) const {
return cost > other.cost;
}
};
vector<Edge> a[1001];
bool c[1001];
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
cin >> m;
for (i = 0; i < m; ++i) {
int from, to, cost;
cin >> from>>to >> cost;
a[from].push_back(Edge({ to, cost }));
a[to].push_back(Edge({ from, cost }));
}
priority_queue<Edge> q;
for (Edge ee : a[1]) {
q.push(ee);
}
c[1] = true;
while (!q.empty()) {
Edge num = q.top();
q.pop();
if (c[num.to]) continue;
c[num.to] = true;
ans += num.cost;
for (Edge ee : a[num.to]) {
q.push(ee);
}
}
cout << ans << '\n';
}이 문제를 풀면서 구조체 내부에 오퍼레이터를 설정할 수 있다는 것을 알 수 있게 되었다. 그러면 이 오퍼레이터에 맞추어 우선순위 큐가 알아서 정렬을 해주기 때문에 매우 편리한 것을 확인할 수 있엇다.
크루스칼
3. DAG (Directed Acyclic Graph)
사이클이 없는 방향 있는 그래프
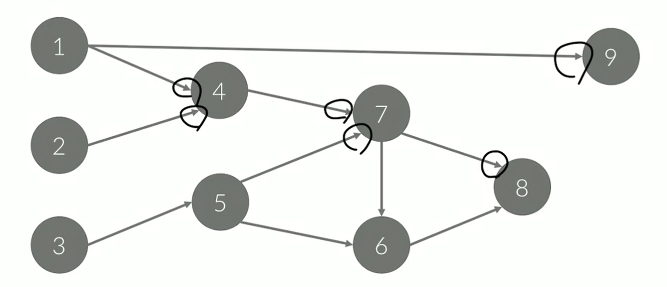
이 그래프를 활용한 다양한 알고리즘이 존재한다.
위상 정렬
BFS>DFS

그래프의 간선 u->v가 u가 v보다 먼저라는 의미일 때 정점의 순서를 찾는 알고리즘, 어떻게 하면 이 조건을 어기지 않을 수 있을지 연구하는 알고리즘이다.
위의 그래프도 [1,2,3,4,5,6,7,8,9]와 같이 만들 수 있을 것이다. 예를 들어 옷을 입는 순서는 어떻게 되어야 제대로 된 순서인지를 알아보는것이 있다.
위상 정렬 알고리즘은 BFS를 응용해서 구현할 수 있다.
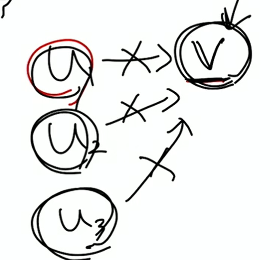
만약 위와 같은 관계를 가지고 있을 때 자식 노드들을 하나씩 제거해 나가면 v의 in-degree는 0이 된다. 이는 곧 이 노드도 함께 지울 수 있다는 것을 의미하게 된다.
위상 정렬에서 가장 중요한 것은 in-degree가 0이 되는 순간이다.
BFS 형태로 노드들을 계속 큐에 넣고 빼고를 반복하며 in-degree가 0이 아니라면 다시 큐에 삽입한다.
ind[i] = i의 in-degree를 저장해 놓고 진행한다.


O(E) -> O(N+E)
필요한 성분 3요소
1. 우선순위 큐
2. indegree를 계산하는 변수
3. 인접리스트 -> BFS로 돌면서 연결된 모든 것을 삽입
DFS 형태로 문제를 풀수도 있다.
그래프의 간선을 모두 뒤집어놓고 DFS를 수행하고 정점이 스택에서 빠져나오는 순서를 기록하면 위상 정렬의 순서와 같아지게 된다.
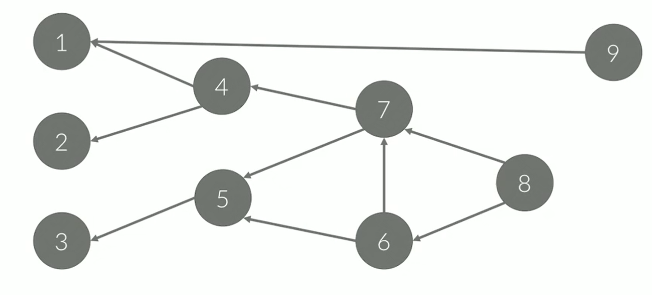
예를 들어 위와 같이 DAG를 뒤집어 놓았을 때 8에서 시작한다면 1까지 쭉 올라갈 수 있을것이다. 그다음 2, 4, 3, 5, 7, 8, 6, 9 순으로 위상정렬될 것이다.

문제
2252 줄 세우기
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i, j, n, m;
vector<int> a[100001];
int ind[100001];
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (i = 0; i < m; ++i) {
int from, to;
cin >> from >> to;
a[from].push_back(to);
++ind[to];
}
queue<int> q;
for (i = 1; i <= n; ++i) {
if (ind[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int num = q.front();
q.pop();
for (int i : a[num]) {
if(ind[i]>0) --ind[i];
if (ind[i] == 0) {
q.push(i);
}
}
cout << num << ' ';
}
return 0;
}1766 문제집
줄 세우기와 차이점은 가능하면 쉬운 문제부터 풀어야 한다이다. 문제번호는 난이도 순이고
- 모든 문제를 풀어야 한다.
- 먼저 푸는게 좋은 문제는 반드시 먼저 출어야 한다.
- 가능하면 쉬운 문제부터 풀어야 한다.
줄 세우기와 동일하게 u->v의 관계를 만족할 수 밖에 없다.
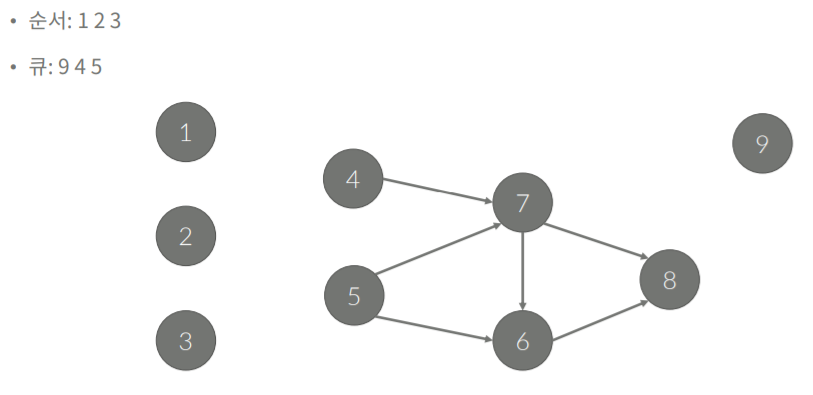
그래서 앞의 그래프는 위와 같이 생기기 때문에 9를 먼저 풀어서는 안된다. 이러한 문제점을 해결하기 위해서 min-heap을 사용해서 문제를 풀면된다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i, j, n, m;
vector<int> a[100001];
int ind[100001];
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (i = 0; i < m; ++i) {
int from, to;
cin >> from >> to;
a[from].push_back(to);
++ind[to];
}
priority_queue<int> q;
for (i = 1; i <= n; ++i) {
if (ind[i] == 0) {
q.push(-i);
}
}
while (!q.empty()) {
int num = -q.top();
q.pop();
for (int i : a[num]) {
if(ind[i]>0) --ind[i];
if (ind[i] == 0) {
q.push(-i);
}
}
cout << num << ' ';
}
return 0;
}