5. 그래프 알고리즘(Graph)

TonyHan·2020년 7월 29일
0

알고리즘

목록 보기
15/23
post-thumbnail

https://webnautes.tistory.com/1158
vscode C++ 환경에 맞추어 PS하기

그래프

그래프 알고리즘은 문제에 나와 있는 상황을 그래프로 모델링한 다음에 여러가지 알고리즘을 수행하게 된다.

그래프 문제 알고리즘은 동일하다.
단지 데이터를 어떻게 그래프로 만들지가 중요하다.

용어

  • 정점(Node, Vertex)

  • 간선(Edge) : 정점간의 관계를 나타낸다.

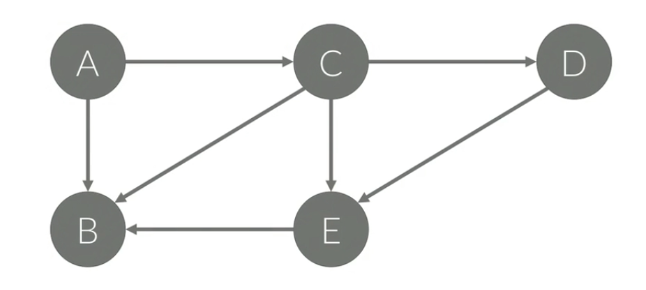
  • 경로 : 정점간의 이동에 대한 간선의 연속을 의미한다.

  • 사이클 : 시작 정점과 도착 정점이 같은 것을 이야기 한다.

  • 단순 경로, 단순 사이클 : 경로/사이클에서 같은 정점을 두 번 이상 방문하지 않는 경로/사이클
    ※ 특별한 일이 없다면 단순 경로/사이클을 의미


  • 방향 그래프, 무방향 그래프 : 보통 무방향도 방향 그래프로 바꾸어 저장함. - 그래서 무방향 그래프를 양방향 그래프라고 부르기도 함
    ※ 만약 간선이 두개이면 두 간선을 서로 다른 간선으로 취급

  • 루프 : 간선의 양 끝 점이 같은 경우

  • 가중치(중요) : 간선에 적힌 값 - 거리, 시간, 비용으로 만약 적혀있지 않다면 가중치는 1로 보면 됨

  • 차수 : 정점과 연결된 간선의 갯수 ( Degree - 방향 : In-degree 들어오는 간선 / Out-degree 나가는 간선)

그래프의 표현

효율의 차이로 인접 행렬과 리스트의 차이를 생각해야 하다. 한 정점 X와 연결된 간선을 효율적으로 찾는 구조.

효율이라는 것은 한정점 X와 연결된 간선을 효율적으로 찾는 것을 이야기 한다.

  1. 인접 행렬 : V x V 의 이차원 행렬 : 가중치 넣을 수 있음. 공간 v^2필요, 한 정점과 연결된 모든 간선을 구하는 시간 - O(v)
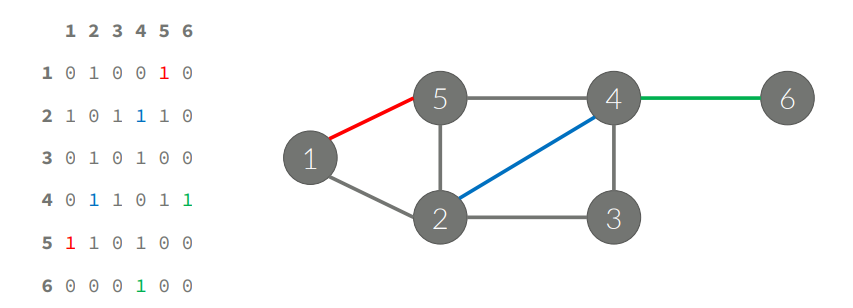
  • 공간 복잡도 : O(V^2)
  • 시간 복잡도 : O(V)

    인접 행렬은 두 정점 사이에 간선이 있는지 없는지만 확인함, 그래서 잘 안씀

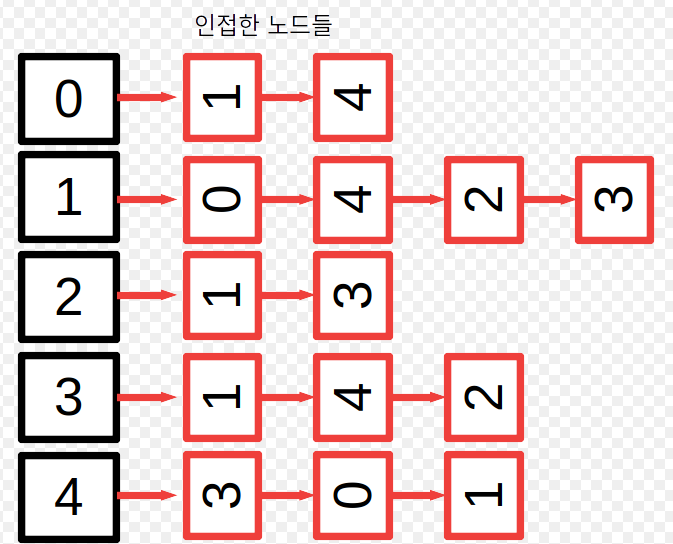
  1. 인접 리스트
    연결되어 있는 정점을 모두 리스트 안에 집어넣음

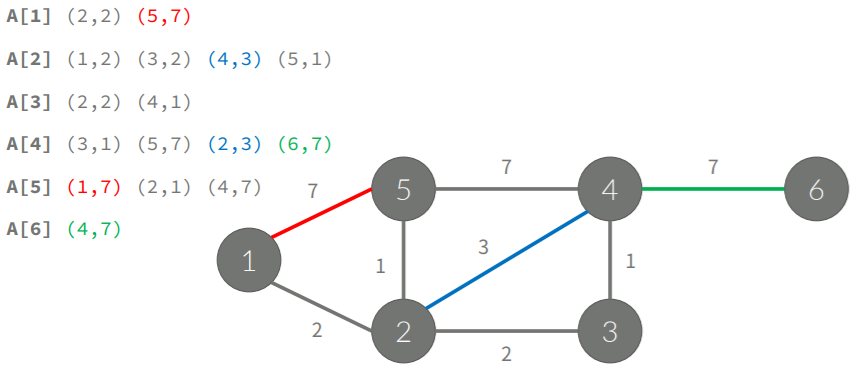
    만약 가중치가 존재한다면 같이 묶어서 저장해 주면 됨 사용하는건 링크드 리스트나 길이를 동적으로 변경할 수 있는 배열을 사용

  • C++ : vector<int> a[1001]

  • Java : Array List

  • Python : [] - 리스트 형태인데 append() 함수때문에 가능

  • 공간복잡도 O(E)

  • 시간복잡도 O(차수)

    인접리스트가 더 적은 공간과 더 적은 시간 사용


  1. 간선 리스트

  • 인접 행렬과 인접 리스트 모두 싫을 때 사용 => 대중적인 자료구조는 아님

  • 배열을 이용해 모든 간선 정보 저장

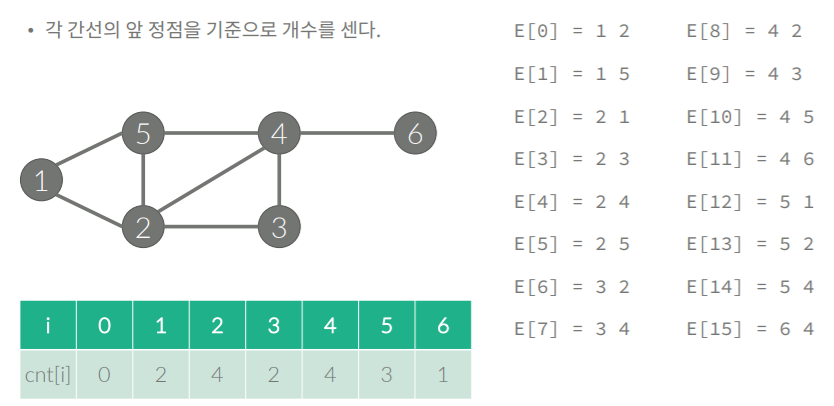
  • 누적의 방식으로 나중에는 배열에 각 노드별 간선 정보를 저장한 칸의 시작위치를 저장 그리고 누적의 방식으로 값을 더해 나아가면 각 정점의 시작 위치를 알 수 있음

  • 시간복잡도 : O(차수)

    정리하면 다음과 같이 선언하면 된다.

  • 인접행령
    bool a[2000][2000]

  • 인접리스트
    vector< int > g[2000];

  • 간선리스트
    vector< pair < int, int >> edges;

문제

13023 ABCDE(대표)

N명의 친구 관계에서 주어진 것과 같은 친구 관계가 존재하는지 알아보는 문제로 세가지의 케이스로 데이터를 모두 저장하여서 사용하게 된다.

  • 인접행렬
  • 인접 리스트
  • 간선 리스트

친구 관계 = 간선으로 구현
A->B, C->D
이때 B->C로 가는걸 찾기 위해 인접행렬을 사용해야 한다.
D->E로 가는 인접리스트를 사용해주면된다.

이때 코드 중간에 m을 두배로 만드는데 이것은 간선의 갯수는 각각 두개씩 넣어주었기 때문에 두배를 해준것이다.

import sys
sys.stdin=open("input.txt","r")

m=0
n=0
n,m=map(int,input().split())

# 인접행렬
a=[[False]*n for _ in range(n)]
# 인접리스트
g=[[] for _ in range(n)]
# 간선리스트
edges=[]

for i in range(m):
    f,t=map(int,input().split())
    a[f][t]=a[t][f]=True
    edges.append((f,t))
    edges.append((t,f))
    g[f].append(t)
    g[t].append(f)

m*=2
for i in range(m):
    for j in range(m):
        A,B=edges[i]
        C,D=edges[j]
        if A==B or A==C or A==D or B==C or B==D or C==D: continue
        if not a[B][C]: continue
        for E in g[D]:
            if E==A or E==B or E==C or E==D: continue
            print(1)
            sys.exit(1)

print(0)

코드는 인접행렬 인접리스트 간선리스트를 모두 사용된 형태로 짜여지기는 하였지만 실재로 이렇게 구현하지 않아도 위의 문제를 푸는데 문제는 없다.

#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <map>
#define ll long long
using namespace std;

bool a[2000][2000];
vector<int> g[2000];
vector<pair<int,int> > edges;

int main(void)
{
    freopen("input.txt", "r", stdin);
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n,m;
    cin>>n>>m;
    for(int i = 0 ; i < m ; ++i)
    {
        int from, to;
        cin>>from>>to;
        edges.push_back({from,to});
        edges.push_back({to,from});
        a[from][to] = true;
        a[to][from] = true;
        g[from].push_back(to);
        g[to].push_back(from);
    }

    m *= 2;
    for(int i = 0 ; i < m; ++i)
    {
        for(int j = 0 ; j < m ; ++j)
        {
            int A = edges[i].first;
            int B = edges[i].second;
            int C = edges[j].first;
            int D = edges[j].second;

            if(A==B || A == C || A == D || B == C || B == D || C == D)
                continue;
            if(!a[B][C])
                continue;
            for(auto E = g[D].begin(); E != g[D].end(); ++E)
            {
                if(*E == A || *E == B || *E == C || *E == D)
                    continue;
                cout<<"1"<<'\n';
                return (0);
            }
        }
    }
    cout<<"0"<<'\n';
    return (0);
}

그래프의 탐색

DFS와 BFS가 존재

void dfs(int node) {
	check[node] = true;
	cout << node << ' ';
	for (i = 0; i < a[node].size(); ++i) {
		int next = a[node][i];
		if (check[next] == false) {
			dfs(next);
		}
	}
}

void bfs(int node) {
	queue<int> q;
	memset(check, false, sizeof(check));
	check[node] = true;
	q.push(s);
	while (!q.empty()) {
		int now = q.front();
		q.pop();
		cout << now << ' ';
		for (i = 0; i < a[now].size(); ++i) {
			int next = a[now][i];
			if (check[next]==false) {
				check[next] = true;
				q.push(next);
			}
		}
	}
}

문제

1260 DFS와 BFS

#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#define ll long long
#define len 1001
using namespace std;

int ans, i, j, n, m,s;
vector<int> a[1001];
bool check[1001];

void dfs(int node) {
    check[node] = true;
    printf("%d ", node);
    for (int i = 0; i < a[node].size(); i++) {
        int next = a[node][i];
        if (check[next] == false) {
            dfs(next);
        }
    }
}
void bfs(int start) {
    queue<int> q;
    memset(check, false, sizeof(check));
    check[start] = true;
    q.push(start);
    while (!q.empty()) {
        int node = q.front();
        q.pop();
        printf("%d ", node);
        for (int i = 0; i < a[node].size(); i++) {
            int next = a[node][i];
            if (check[next] == false) {
                check[next] = true;
                q.push(next);
            }
        }
    }
}
int main() {
    int n, m, start;
    scanf("%d %d %d", &n, &m, &start);
    for (int i = 0; i < m; i++) {
        int u, v;
        scanf("%d %d", &u, &v);
        a[u].push_back(v);
        a[v].push_back(u);
    }
    for (int i = 1; i <= n; i++) {
        sort(a[i].begin(), a[i].end());
    }
    dfs(start);
    puts("");
    bfs(start);
    puts("");
    return 0;
}

2667 단지번호 붙이기

  • 그래프 같지 않은 문제를 그래프로 바꾸어 푸는 예시
  • 4방향에 대해 BFS 를 수행하면 풀기 때문에 어렵지 않게 풀 수 있음
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define ll long long
using namespace std;

int a[30][30];
int check[30][30];
int dx[4] = { 0,0,-1,1 };
int dy[4] = { -1,1,0,0 };
int n;
int cnt[25*25] = { 0 };

void bfs(pair<int, int> x,int ans) {
	queue<pair<int, int>>q;
	q.push(x);
	check[x.first][x.second] = ans;
	while (!q.empty()) {
		pair<int, int> cur = q.front();
		q.pop();
		for (int i = 0; i < 4; ++i) {
			pair<int,int> next = {cur.first+dx[i],cur.second+dy[i]};
			if (0 <= next.first && next.first < n 
            			&& 0 <= next.second && next.second < n) {
				if (a[next.first][next.second] == 1 
               	 			&& check[next.first][next.second] == 0) {
					q.push(next);
					check[next.first][next.second] = ans;
				}
			}
		}
	}
}


int main(void) {
	//freopen("input.txt", "r", stdin);
	int t; 
	cin >> n;
	 
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n; ++j) {
			scanf("%1d", &a[i][j]);
		}
	}

	
	int ans=0;
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n; ++j) {
			if (a[i][j] == 1 && check[i][j] ==0) {
				bfs(make_pair(i, j), ++ans);
			}
		}
	}
	cout << ans<<endl;

	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n; ++j) {
			cnt[check[i][j]] += 1;
		}
	}

	sort(cnt+1, cnt+ ans+1);
	for (int i = 1; i <= ans; ++i) {
		cout << cnt[i] << endl;
	}
	return 0;
}


4963 섬의 갯수

  • 비슷하게 bfs를 사용하지만 8방향 즉 대각선까지 사용하면 되기 때문에 조금만 응용해서 풀면 됨


#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define ll long long
using namespace std;

int a[51][51];
int check[51][51];
int dx[8] = { -1,0,1,1,1,0,-1,-1 };
int dy[8] = { -1,-1,-1,0,1,1,1,0 };
int n,m;
//int cnt[50*50] = { 0 };

void bfs(pair<int, int> x,int ans) {
	queue<pair<int, int>>q;
	q.push(x);
	check[x.first][x.second] = ans;
	while (!q.empty()) {
		pair<int, int> cur = q.front();
		q.pop();
		for (int i = 0; i < 8; ++i) {
			pair<int, int> next = {cur.first+dx[i],cur.second+dy[i]};
			if (0 <= next.first && next.first < m 
            			&& 0 <= next.second && next.second < n) {
				if (a[next.first][next.second] == 1 
                			&& check[next.first][next.second] == 0) {
					q.push(next);
					check[next.first][next.second] = ans;
				}
			}
		}
	}
}


int main(void) {
	freopen("input.txt", "r", stdin);
	
	//m:y, n:x
	while (1) {
		scanf("%d %d", &n, &m);
		if (n == 0 && m == 0) break;

		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				scanf("%1d", &a[i][j]);
				check[i][j] = 0;
			}
		}

		int ans = 0;
		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				if (a[i][j] == 1 && check[i][j] == 0) {
					bfs(make_pair(i, j), ++ans);
				}
			}
		}
		printf("%d\n", ans);

	}
	return 0;
}


2178 미로 탐색

  • DFS는 사용 불가 -> 탐색이 완전 랜덤이라서 최소를 찾아내는 문제에는 좋지 못함

  • BFS의 단계별 풀이를 이용하여야 함

  • 이와 같이 한 칸 간 것을 한 단계 간걸로 생각해 볼 수 있기 때문에 BFS는 단계별 풀이가 가능



profile
TonyHan
신촌거지출신개발자(시리즈 부분에 목차가 나옵니다.)
이전 포스트

5. 트리

다음 포스트

5. 그래프(2)

0개의 댓글