https://jbhs7014.tistory.com/entry/ML-Knowledge-Representation

12.3.1 Process

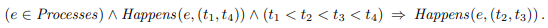
위와 같이 t1에서 t4로의 사건이 있었다라고 할때의 과정을 이야기 한다.

12.3.2 Time intervals

정확한 시간을 이야기 할 수도 있지만 언어적인 일정시간이 존재할 수도 있다.

예시로 위와 같이 2001년 1월에서 발생한 사건에 대해서도 이야기 할 수 있다.

12.3.3 Fluents and objects

Fluent : 계속되는 관게를 나타낼때 사용된다.

T(Equals(President(USA), GeorgeWashington), AD1790) .

예시로 위와 같이 존재할때 Equals를 ==으로 표현해도 되지만 Function Simbol을 사용하여 True이다라고 표현한 것이다.

12.4 Mental Events And Mental Objects

위의 event가 physical한 것을 다룬 것이라면 여기에서는 시각적으로 볼 수 없는 사건들에 대해서 다룰 것이다.

그래서 여기에서 사용하는 Logic이 Modal logic이 존재한다. 이는 양상 논리라고 부른다. Modal logic은 특별한 기술을 사용한다기 보다는 2 + 2 = 4 and 4 < 5와 같이 정신적으로 당연한 것들을 referential transparency 라고 부른다. 참고하는 기준에서 뚜렷하다. 분명하다라는 의미이다.

또다른 예시를 통해 이해해보자

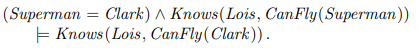
위와 같은 superman이 Lois를 알고 있다라는 Logic이 존재한다. superman=clark라는 것이 사실이고 Superman이 Lois를 알고 있다는 것이 절대적인 사실인지를 알 수 없다. 그렇기 때문에 이를 표현하기 위한 Knows라는 표현을 mental적으로 묘사하였다.

그렇기에 Modal Logic이라는 것이 완전 새로운 Logic을 이야기 하는 것이 아닌 당연한 것들을 이야기 한다는 것을 어느정도 이해할 수 있다. 그렇기에 이런것을 referential Opacity라고 부른다.

12.5 Reasoning Systems For Categories

카테고리에 관련된 추론시스템

12.5.1 Semantic Networks

Semantic networks(의미망) :

∀x x∈Persons ∧x != John ⇒ Legs(x, 2)
어떤 상황에서 공통적인 것을 수식할때 카테고리를 위한 Default values을 표현하는 방법으로 Default value를 일반적으로 공통된 value들을 표현한다.

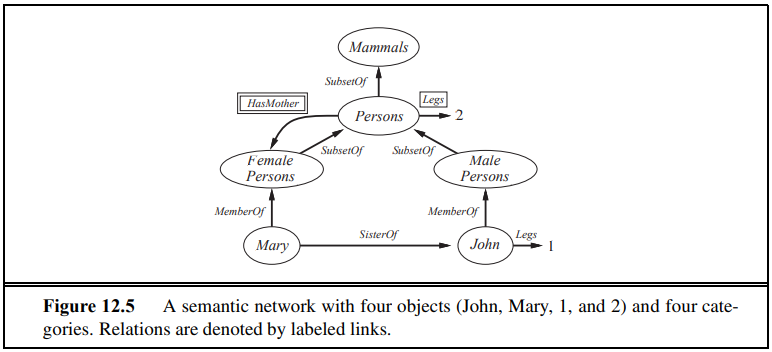
예르 들어 위와 같이 Default한 설정들을 만들 수 있을 것이다. 하지만 위와 같은 Semantic Network의 문제점은 이렇게 하나씩 다루었을 때 경우의 수가 무한히 많아진다는 것이다.

multiple inheritance : 하위의 속성이 상위에서부터 전달되는데 이게 다른 카테고리의 sub 카테고리일 수도 있다. 이때 상위의 모든 카테고리들이 상속되면서 공통된 속성들이 함께 상속되는 것을 이야기 한다.

12.6 Reasoning With Default Information

12.6.1 Circumscription and default logic

circumscription은 조건에 대해서 한정을 짓는 것을 말한다. 이 때 특별한 말이 없으면 변화가 없고 다르지 않다는 뜻임을 가정한다.

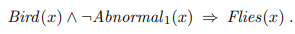
not abnormal(x)로 별도의 언급이 없으면 normal이라고 한정짓는다. 또한 abnormal인 set에 대해서 속성을 한정하거나 다른 속성을 추가할 수 있다.

---

Default Logic은 전제 조건으로부터 결론을 도출해내는 과정에서 consistent conditions의 영향을 받는 것을 말한다. 만약 consistent conditions에서 하나라도 false라는 것을 증명할 수 있다면 전제 조건으로부터 결론을 낼 수 없다.

deault theory는 (D, W)의 페어로 나타나는데 D는 default rule을 의미하고, W는 first-order logic을 의미한다. 여기서 나올 수 있는 결론의 최대 집합을 extension이라고 한다.

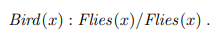
위와 같은 것을 이야기 한다.

12.6.2 Truth maintenance systems

---

12.8 Summary

frames : sementic nets을 위한 자료구조로 표현하기 애매한 경우들까지 모두 나타낼 수 있다.

각 node에서 이 자료구조를 사용하면 모든 경우를 나타낼 수 있다.

Qualitative physics

13. Quantifying Uncertainty

Quantifying Uncertainty : 정량 불확실성이라는 뜻으로 할 수 있는 대상으로 Quantifying 한다는 의미를 가지고 있다.

belief state :