기초 인공지능 07

TonyHan·2020년 9월 23일

20) 기초인공지능

목록 보기

7/21

3.5 Informed (Heuristic) Search Strategies

Informed Search는 Stat-Space(상태 공간)의 가지에서 가장 전도유망한 방향으로 Search를 진행하는 방식을 이야기 합니다.

전에 말했든 Blind Search에서는 전체 상태를 경험적으로 분석할 수 없기에 Goal State로 향하는 어떠한 방향성을 가지고 있지 ㅇ낳고 모든 방향으로 뻗어나간다고 하였다.
이 Informed Search는 Blind Search의 단점을 극복하기 위해 나타났다.

h(n) = estimated cost of the cheapest path from the state at node n to a goal state : n 노드 state에서 목표 state 까지 가는 최소 비용이 드는 경로를 탐색

3.5.1 Greedy best-first search

목표 상태에 가장 근접하게 해주는 노드를 향해 확장하는 알고리즘으로. 해결책을 빠르게 구해냅니다. 그렇기 때문에 f(n) = h(n)의 구성을 가지게 됩니다.

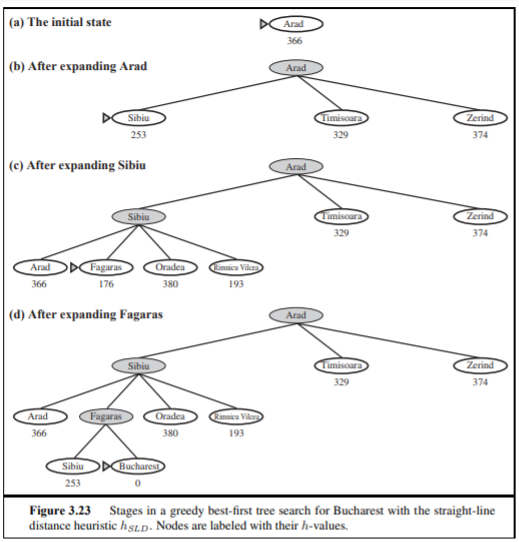
예를 들어서 Arad 에서 bucharest 까지 갈때 위와 같이 각 도시별 bucharest까지의 거리가 주어졌다면 Arad에서는 Sibiu를 먼저 선택하게 된다. 왜냐하면 Sibiu가 Arad에 연결되어 있는(Timisoara,Zerind,Sibiu) 중에 가장 값이 작기 때문이다.

하지만 이게 최선의 선택지가 아니기 때문에 Greedy best-first search 에서는 경로를 찾기 위해 h_SLD를 사용합니다. H_SLD는 휴리스틱을 직선 거리로 잡습니다.

3.5.2 A* search : Minimizing the total estimated solution cost

가장 널리 알려진 best-first search 은 A* Search가 있다.

목표에 도달하는 비용을 f(n)이라고 하면 다음 공식이 성립한다.
f(n) = g(n) + h(n)

g(n) : 노드에 도달하는 비용
h(n) : 한 노드에서 목표상태까지 도달하는 비용
이때 f(n) 은 예상 측정된 값임에도 가장 적은 비용이 적게드는 것을 전재로 하여 f(n)을 설정

Conditions for optimality : Admissibility and consistency

휴리스틱을 얼마나 잘 만드느냐에 따라서 A* 의 성공 활률이 달라짐

first condition
우리가 처음으로 최적화 해야하는 첫번쨰 조건은 h(n) = admissible heuristic 이다. (목표까지 가는 비용을 과대하게 넘지 않는 적절한 알고리즘이어야 한다는 조건) 즉, 아주 객관적인 휴리스틱을 설정해서 누구나 인정할 수 있어야 함. 아까 Greedy Best-First Search 에서 H_SLD는 휴리스틱을 직선 거리로 잡는다고 하였다. 만약 Straight Line이 아니라 빙빙 돌아가는 경로로 휴리스틱을 설정한다면 실제 Goal 까지의 거리보다 경로가 길어지게 휴리스틱을 잡을 수 있다. 그러면 이 '허용성'을 만족시키지 못한다.
second condition
약간 더 강화된 조건 consistency (= monotonicity) 휴리스틱 함수는 consistency 하다. 모든 노드 n에서 a라는 행동을 하여 그 다음 노드 n' 으로 간다면 다음과 같이 n에서의 목표로 가는 비용은 n에서 n'으로 가는 행동의 비용과 n'에서의 목표로 가는 비용을 넘길 수 없다.

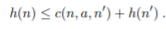
이러한 형태를 triangle inequality라고 부른다.

정리하자면
Admissible Heuristic은 목표로 도달하는 비용이 과대평가되지 않는 휴리스틱
Consistent Heuristic은 현재 H(n) <= 자식 노드로 가는 거리 + 그 자식노드의 H(n)을 유지하는 휴리스틱

이라고 할 수 있음.

Optimality A* (시험)

the tree verion of A 은 h(n) is admissible하기만 하다면 최적이다.
반면 the graph-search version of A 은 h(n) is consistent 하면 최적이다.

first step
h(n)이 consistent 하다면 f(n)을 통하는 어떠한 경로도 nondecreasing 하다.
이를 증명하여 보면

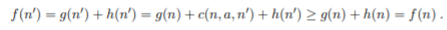
그렇기 떄문에 A* 알고리즘은 어디로 가나 그 값이 줄어들지 않는다. 왜냐하면 노드 n과 그 자식 노드 n'이 있을 떄 Consistency가 보장되어 위와 같은 수식이 완성되기 때문이다.

3.5.3 Memory-bounded heuristic search(시험)

너무 노드가 많은것도 문제이기 때문에 주어진 범위에서 heuristic search를 하여야 한다는 이야기이다. 정확히는 메모리를 한정함으로 아까운 메모리를 무작정 퍼 나르는 것이 아니라 어느 정도의 메모리만 사용하겠다는 것을 암시한다. 즉, A* 를 사용할 때 보다 메모리를 절약할 수 없겠느냐를 고려해서 나온 방법들이다.

이때 알고리즘을 공부할 때 자주 나오는 반복(iterative)와 재귀(Recursive)의 개념이 들어간다.
ex>

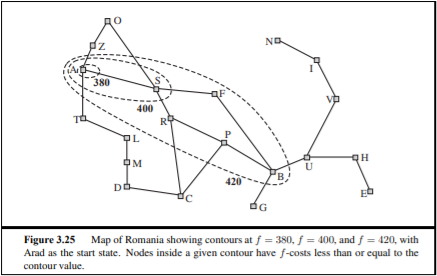
위의 경우도 Memory-bounded하다고 볼 수 있다. 일정한 값을 기준으로 그 범위를 넘지 않는 경로들을 등고선을 이용하여 표현하기 때문이다.