3.6 Heuristic Functions

이번 단원에서는 휴리스틱 알고리즘의 정확도 측정에 대해서 다루어 보자

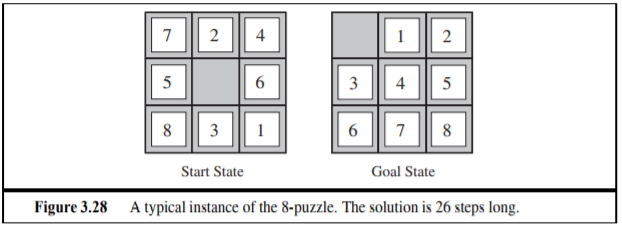
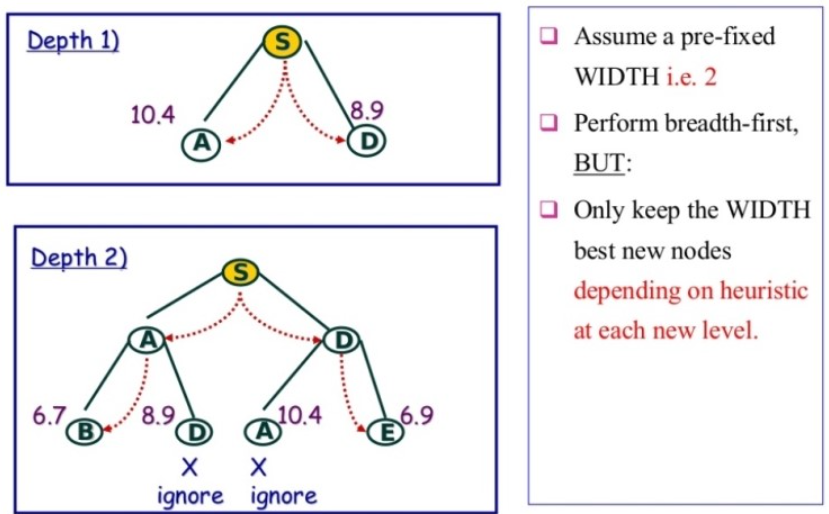
위의 예는 8puzzle 문제로 8개의 퍼즐을 욺직여서 원하는 결과가 나오도록 맞추는 것이다. 이때의 exhaustive tree search의 깊이는 22 까지 간다. 이는 3^22 = 3.1 * 10^10 의 연산이 필요하다는 결론이 생기게 된다.

A* 를 활용한 가장 짧은 해결책을 우너한다면 우리의 목표보다 과대 평가되는 휴리스틱을 사용해서는 안된다.

최종적으로 다음 두자기 값을 채워 넣는데
h_1 : 현재 잘 못 놓아진 타일의 갯수를 계산한 값이다.
h_2 : 각 타일별로 목표로 하는 위치까지 가는 거리의 합을 이야기 한다. 우리가 타일을 원하는 위치로 이동시킬 수록 h_2 의 값은 점차 목표로 했던 값으로 가까워 진다.

3.6.1 The effect of heuristic accuracy on performance

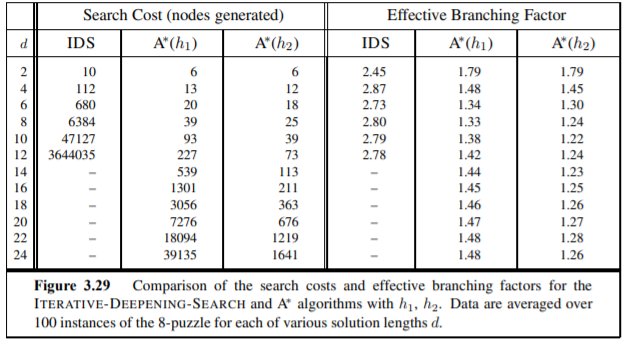
위의 표는 h_1과 h_2 의 depth 별로 구해지는 효율성과 비용 지표를 볼 수 있는데 깊이가 깊어질 수록 비용은 h2 를 사용했을 때 그 비용이 점차 감소하고 동시에 사용하는 가지의 수 즉 효율성역시 h2가 좀 더 나은 결과를 보여주는 것을 확인 할 수 있다.

3.6.2 Generating admissible heuristics from relaxed problems

3.6.3 Generating admissible heuristics from subproblems: Pattern databases

그때그때 상황에 맞추어 해결책을 만들어 놓으면 그 다음 부터는 직접 search를 통하지 않고도 목표까지 도달할 수 있다.

3.6.4 Learning heuristics from experience

Inductive learning methods(귀납적 학습) : 우리가 원하는 상태의 features(특징) of a state을 최대한 많이 전달함으로써 작동이 이루어 진다. 예를 들어서 얼굴인식과 같이 사람의 특징을 많이 가지고 있어야지 인공지능이 그 물체를 사람으로 인식하지 만약 가지고 있는 특징들이 적다면 인식되는 사물이 다른 것으로 인식이 될 수도 있다.

---

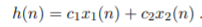
4. Beyond Classical Search

4.1 Local Search Algorithms And Optimization Problems

local seach : 전체 공간에서 부분적인 탐색을 하고 또 다른 지역에 가서는 method strategy를 수행할 수 있다는 의미에서 local search라고 부름. 그렇기에 Local Seach Algorithms는 순수한 최적화 문제를 해결할 떄 유용함. 최적화에 있어서 목적은 Objective Function(목적 함수)에 따라서 Best State를 찾는 것입니다. 최적화 문제는 항상 문제를 탐색하는 것이 아닙니다. 따라서 결과적으로 항상 Final Goal State가 존재하는 것이 아닐 뿐 아니라 이 Local Search에서는 경로와 비용 따위는 별로 중요하지가 않음.

이러한 Local Search 같은 경우는 목적 함수라는 것을 이용해 현재 노드를 기준으로 이웃 노드들을 확인하여 조금이라도 더 좋은 노드로 이동을 하는 방식을 이용함

하지만 자기가 지나온 경로들은 조금도 유지하고 있지 않습니다. 이때 Local Search 알고리즘이 조금 덜 체계적이라면 두가지 장점이 있슴

1. 아주 적은 메모리를 이용
2. 무한하거나 아주 큰 상태 공간에서 그나마 합리적인 해를 찾아내는 이점

여기에서 말하는 것과 같이 모든 경우의 찾는 것은 불가능 그렇기 떄문에 그냥 경우의 수들 중 적절한 거를 뽑아서 준다고 쉽게 생각해 볼 수도 있음. 따라서 여기서 사용되는 것들은 전까지 배워왔던 Standard한 탐색 모델들이 아니라는 이야기, 다른 말로 하면 여기서는 Goal Test와 Path Cost의 개념이 없어짐.

목적 함수 값의 최적화는 종종 상태 공간 산맥으로 형상화가 이루어짐

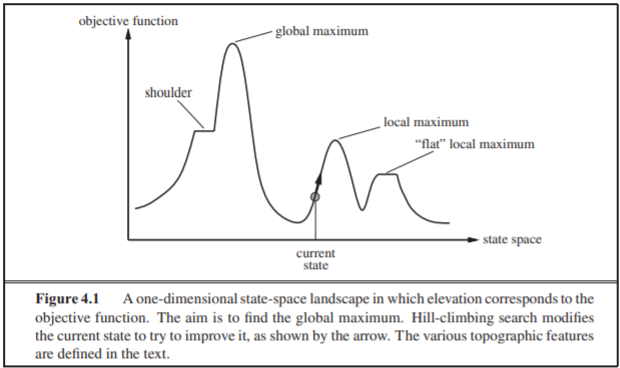
함수의 값이 가장 크다면 그것은 산맥의 꼭대기에 해당될 것임. 여기에서 몇 가지 중요한 용어가 나옴
1. Global Maximum : 극대화 문제의 최적화된 해(최대값)
1. Local Maximum : 주변의 값들 사이에서 가장 높은 꼭대기(극댓값)

우리는 현재 Local Maximum을 찾는 것이 중요하기 때문에 이를 찾는 유명한 Local Search 는 다음 4가지가 존재함

1. Hill-Climbing Search
2. Simulated Annealing
3. Local Beam Search
4. Genetic ALgorithms

4.1.1 Hill-climbing search(언덕 오르기 탐색)

현재 노드를 기준으로 주변 노드 중에서 더 올라갈 곳이 있으면 이동을 하는 알고리즘으로 나중에 더이상 올라갈 곳이 없으면 그곳을 Peak(꼭대기) 라고 간주함

마치 등산을 할 때 경로가 갈리었다면 일단 한 쪽으로 올라간다면 그곳이 높은 곳이기는 하지만 산 정상중에 가장 높은 곳인지 알 수 없는 것과 비슷합니다.

Search Tree를 가지고 있을 필요도 없고 이전 State들의 정보를 가지고 있을 필요도 없습니다.

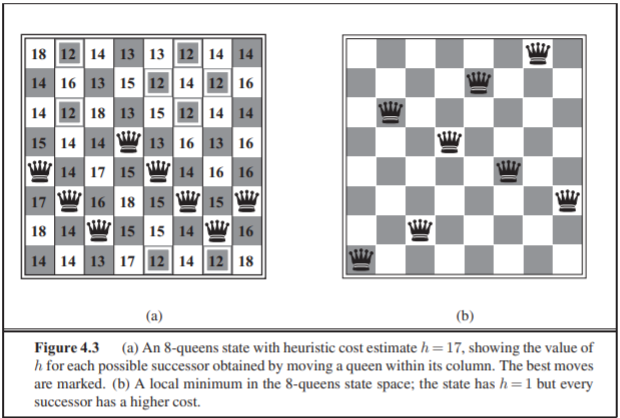
이러한 search의 대표적인 예가 8-Queens입니다.

여기서는 Complete-State Formulation을 사용할 수 있습니다. 한 Column에 단 하나의 퀸만 들어간다는 공식화(Fomulation)이 이루어진 결과물 입니다.

Hill Climbing 은 가끔 Greedy Local Search 라고도 합니다. 탐욕 Local Search라는 이야기 입니다.

이러한 Hill Climbing Search는 보통 아주 빠릅니다.
하지만 3가지 문제점이 있습니다.

1. Local Maxima(지역 최대치 - 오타 아님) : Global Maximum에 도달하지 못하고 Local Maxuimum 안에 갇힐 수도 있다.
2. Ridges(능선) : 날카로운 능선에 위치하고 있으면 동, 서, 남, 북 어디로 이동하더라도 고도가 낮아져서 Peak로 잘못 판단 할 수 있다.
3. Plateau(고원) : 평평한 곳(Shoulder)에 머물리 있으며 어디로 이동할 지 판단할 수 없다.
   
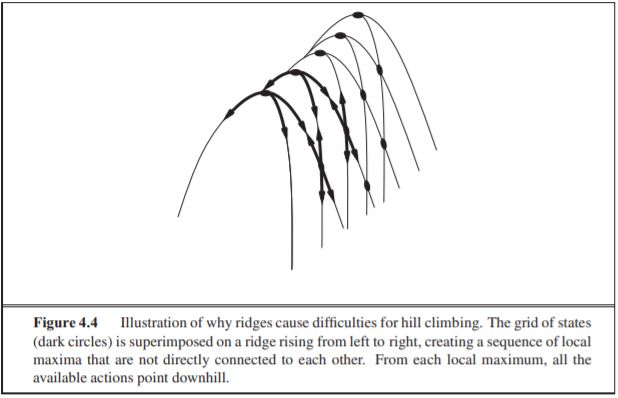
   위의 사진은 Ridge의 문제점을 보여줍니다. 당장 능선 중 동,서,남,북 어디로 향하더라도 더이상 올라갈 수 있는 방향이 없습니다.

결국 Hill Climbing 은 Optimality를 보장할 수 없기 때문에 별로 신뢰성이 높지 않다고 볼 수 있습니다.

하지만 반대로 알고리즘 자체가 정말로 단순하면서 계산의 부하가 적다는 장점이 있어 이 Hill Climbing Search를 계속해서 채택하기 위해 문제점을 해결할 수 있는 여러 방법이 나왔습니다.

1. Stochastic Hill Climbing
   이는 매 번 최적의 이웃을 선택하지 않고 현재 상태보다 나은 이웃 중에 하나를 임의로 선택하는 겁니다. 즉, 이웃 중에서 괜찮을 걸로 그냥 하나 아무거나 집어 들어서 이동하는 것입니다. 이것은 단순히 보면 Hill-Climbing보다 알고리즘 자체는 비효율적이지만 결과 자체는 더 높은 Maximum을 채택하는 경우의 수가 늘어나게 됩니다.
2. First-Choice Hill Climbing
   만약에 이웃 노드의 수가 몇 만개 이상 된다면 그것을 다 뒤져서 가장 좋은 것을 고를 수 없기 때문에 그냥 현 상태보다 조금이라도 나은 상태가 나오면 바로 그 상태를 채태개서 사용하는 CLimbing Search 방법
3. Random-Restart Hill Climbing
   다양한 Hill-Climbing 알고리즘들을 여러 번 반복해서 그 중 가장 좋은 해답을 택하는 Search 방법

4.1.2 Simulated annealing

Hill-Climbing 알고리즘은 Local Maximum에 빠질 수 있다는 단점이 있기 때문에 이 Simulated Annealing(가열 냉각)은 가열 냉각하는 과정을 알고리즘처럼 사용해서 꽤나 괜찮은 목표 상태에 이르는 방법입니다.

만약에 봉우리를 만났을 때 다시 갈림길까지 내려가서 다른 봉우리로 이동한다면 어떻게 될까요? 이것이 지금 말하는 Simulated Annealing에 관한 것입니다.

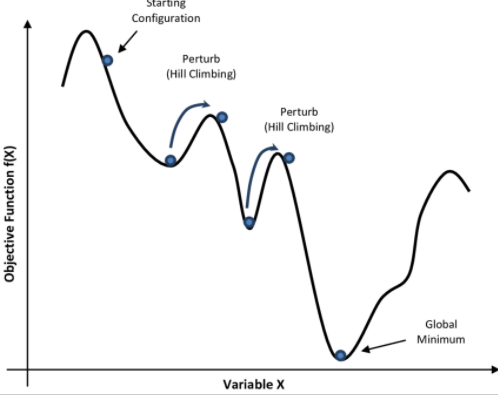
(출처 : http://www.cs.us.es/~fsancho/?e=206)

• 방법

1. 우선 기존의 등산 지도를 뒤집습니다. 그러면 가장 낮은 계곡이 Global Maximum처럼 보이게 될것입니다. 그 다음 쉽게 말해 이 Simulated Annealing은 공을 굴린 뒤에 전체 지도를 마구 흔드는 겁니다. 그럼 공이 사방 팔방으로 튈것입니다.
2. 이제 지도를 흔드는 속도를 천천히 낮춥니다. 그럼 마지막에는 어떤 계속에 빠지게 될겁니다. 그 계곡을 가장 합리적인 Goal로 보는 것입니다.

이러한 방식으로 처음 Local Maximum에 빠지더라도 마지막에는 Global Maximum으로 돌아가게 될 것입니다.

이 과정이 오히려 초기의 극대값 상태를 빠져나와서 오히려 더 안 좋은 상태로 빠지게 할 수 있는데, 온도가 낮아질 수록 최대값 상태가 될 확률이 높아진다고 볼 수 있습니다.

구체적인 알고리즘은 다음과 같습니다.
1. 이웃한 상태 노드 중에서 임의로 상태 하나를 선택합니다.
1. 그 뒤에 해당 상태가 현 상태보다 낫다면 바로 전이를 시작하고 혹시 더 안좋다면 '온도'와 더 안좋아지는 정도를 가지고 전이할 지 말 지를 따지게 됩니다.

이때 온도가 T 더 안좋아지는 정도가 df(x)라 한다면
확률은 e^(-df(x)/T) 라고 합니다.

이 Simulated Annealing 알고리즘은 온도가 충분히 느리게 낮아진다면 Optimal 하다는 것이 증명되었으나
충분히 느리다는 말과 같이 속도가 느리어서 실재로 사용하기에는 무리가 있는 알고리즘 입니다.

4.1.3 Local beam search(시험)

Local Beam Search는 Best-First Search에서 기억 노드의 수를 제한하는 방법임

이 탐색 방법은 기억 공간을 축소시키기에 굉장히 유리하지만 가지치기가 지나치게 빠름.

실제로 사용하는 방법은 먼저 BFS Search로 다음 상태의 해 집합을 구한 뒤에, 해 집합을 Goal에 가까운 순서대로 정렬함. 그리고 사전 설정된 수 만큼의 해 집합을 유지하고 나머지는 잘라내는 방법임

좀 더 구체적으로 말하자면
시험

1. 무작위로 생성된 State들인 K에서 시작함
2. 각 단계에서 모든 K의 자손 노드를 생성함
3. 자손 노드 중에서 어느 하나가 목표인 경우 알고리즘은 해를 찾음
4. 그렇지 않으면 목록에서 K의 최선의 자손 노드를 선택하고 이를 반복
5. Beam 탐색의 병렬 검색은 가치가 없는 자손 노드를 빠르게 제거하고 가장 그럴싸한 노드로 이동할 수 있게 해줌
6. 확률적인 Beam 탐색에서는 유지된 자손 노드들이 그들의 효용성을 기반으로 선택

참고문헌 : https://blog.naver.com/ndb796/220578912459