중간고사는 4장까지

5. Adversarial Search(시험 X)

내가 어떤것을 찾아나가더라도 그것을 막는 장애물들을 고려하는 탐색방법이다.

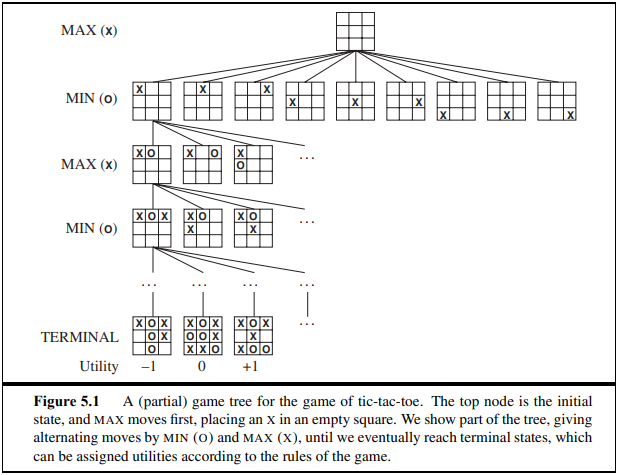
위와 같이 틱택톡 게임이 존재할때, MIN은 상대방이 선택할 수 있는 경우의 수를 최소한으로 줄일 수 있는 방법을 고안한다는 의미에서 MIN이라고 호칭한다.
그리고 그 다음의 MAX는 그 다음에 내가 선택할 수 있는 경우의 수를 최대화 하여서 선택한다는 의미에서 MAX라고 부른다.

그래서 이번 단원에서는 특벽한 알고리즘을 다룬다기 보다는 현재의 상태에서 최대 혹은 최소의 경우를 따지어 봄으로써 상태공간을 줄이는 경우를 찾는 것이다.

---

CSP는 이번 강좌에서 더욱 효과적으로 다양한 문제의 해결을 도모하는 방법을 제시해줍니다. 지금부터 우리는

요소적인 묘사(Factored Representation)를 각각의 상태(값을 가지고 있는 변수들)에 사용할 것입니다.

여기에서 하나의 문제는 변수에 걸린 모든 제약 조건을 만족하는 변수 값을 가지고 있을 때 해결이 완료됩니다.

6. Constraint Satisfaction Problems

Constraint Satisfaction Problems(CSP)란

'특정한 상황이 변수를 제약하는 상황에서 그러한 제약 조건을 모두 만족시키는 변수의 쌍을 구하는 문제'를

의미합니다. CSP 알고리즘들은 특별한 문제의 휴리스틱을 이용하는 것보다는 일반적인 목적의 휴리스틱을 이용합니다.

즉, State의 구조적인 측면에서 이익을 취할 수 있습니다. CSP의 주요 아이디어는 탐색 공간의 많은 부분을

제약 조건을 완화하는 변수 값 조합을 구체화함으로써 제거하는 것입니다.

이번 장은 다음 4가지를 다룸으로써 CSP를 해결하는 방법에 대해서 논하겠습니다.

1. Defining Constraint Satisfaction Problems

2. Constraint Propagation : Interference in CSPs

3. Backtracking Search For CSPs

4. Local Search For CSPs, Structure of Problems

6.1 Defining Constraint Satisfaction Problems

1. Defining Constraint Satisfaction Problems (CSP 정의)

CSP는 X, D 그리고 C 이렇게 3가지 구성요소로 정의될 수 있습니다.

X : 변수들의 집합을 의미합니다. { X1, ..., Xn }

D : 변수 값의 영역의 집합을 의미합니다. { D1, ..., Dn }

C : 가능한 값들의 조합을 구체화하는 제약 조건의 집합을 의미합니다.

각각의 영역 Di는 가능한 값들의 집합을 포함합니다. { V1, ..., Vk }는 각각의 변수 Xi에 들어갑니다.

또한 각각의 제약 조건 Ci는 < Scope, Rel > 형태의 한 쌍을 가지고 있습니다.

여기서 Scope는 값들의 튜플을 의미하고 Rel은 변수가 가질 수 있는 값의 관계(제약 조건)를 정의합니다.

마치 데이터베이스와 비슷하게 보일 수도 있습니다.

예를 들어서 X1와 X2가 영역으로 { A, B }를 가질 수 있을 때 두 변수의 값이 같으면 안된다는 제약 조건이

걸려있다고 가정합시다. 이 때 제약 조건 C는 다음과 같이 정의할 수 있겠죠.

<(X1, X2),[(A,B),(B,A)]> 혹은 <(X1, X2), X1 != X2>

CSP를 해결하기 위해서는 상태 공간을 정의하고 해를 정확히 구해야겠죠.

CSP에서 사용되는 State들은 모든 변수들의 값의 배열로써 정의될 수 있습니다.

예를 들면 { Xi = Vi, Xj = Vj ... } 이렇게 말이죠.

여기서 각각의 배열은 다음과 같이 설명할 수 있습니다.

일관적인 배열(Consistent Assignment) : 어떠한 제약 조건도 위반하지 않는 배열

완전한 배열(Complete Assignment) : 모든 변수가 정렬되어 CSP의 해답을 제공하고 완전하고 일관적인 배열

부분적인 배열(Partial Assignment) : 오직 몇 개의 변수만 값을 정렬해놓은 배열

< Map Coloring >

여기서는 주로 Map Coloring을 예시로 들어서 설명합니다.

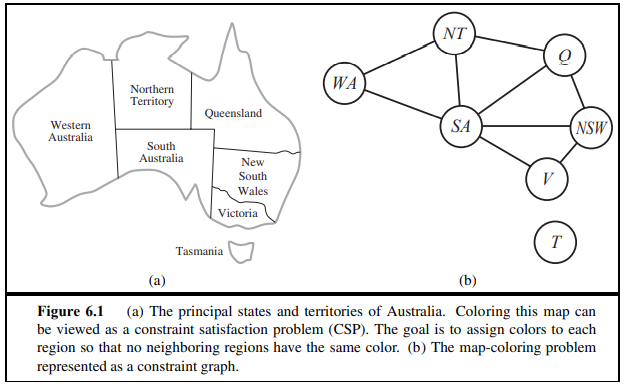
위 그림은 CSP로서 제시된 지도 색칠하기 예시입니다. 목표는 주변 도시가 같은 색으로 색칠되지 않는 것입니다.

(a)는 조금 더 구체적으로 그려진 예시고 (b)는 제약 그래프(Constraint Graph)로서 나타내진 문제입니다.

중학교 때 많이 풀던 수학 경우의 수 문제와 비슷하죠?

만약에 Red, Green, Blue 세 가지 색깔이 주어졌다고 가정했을 때 어떻게 색칠하면 좋을지 알아봅시다.

먼저 CSP의 구성요소 3가지로 정의하도록 하죠.

X = { WA, NT, Q, NSW, V, SA, T } : 각각의 변수들

D = { RED, GREEN, BLUE } : 변수가 가질 수 있는 값의 영역

C = { SA != WA, SA != NT, SA != Q, SA != NSW, SA != V, WA != NT, NT != Q, Q != NSW, NSW != V } : 변수 값들의 제약 조건

여기서 우리는 축약(Abbreviation)을 이용했습니다. SA != WA는 <(SA, WA), SA != WA>의 줄임말이죠.

SA != WA는 더 구체적으로 다음과 같이 열거할 수 있습니다.

{(RED, GREEN), (RED, BLUE), (GREEN, RED), (GREEN, BLUE), (BLUE, RED), (BLUE, GREEN)}

사실 이 문제의 답은 아주 많은 형태로 가능합니다. 예를 들어,

{ WA = RED, NT = GREEN, Q = RED, NSW = GREEN, V = RED, SA = BLUE, T = RED }와 같이 말입니다.

이러한 CSP를 Constraint Graph로 시각화하면 꽤 많은 도움이 될 수 있습니다.

그림 (b)를 보면 제약 그래프가 그려져있습니다. 각각의 노드들은 노드의 변수와 상응하는데요.

각각 연결되어 있는 링크는 두 변수 간의 제약조건을 구성합니다.

왜 문제를 CSP로서 공식화하는 것일까요? 한 가지 이유는 CSP들이 다양하고 넓은 문제를

자연적으로 묘사할 수 있기 때문입니다. 만약에 CSP 문제 해결 시스템을 가지고 있다면

문제를 해결하는 것은 더 쉬울 것입니다. 다른 탐색 기술보다 훨씬 실제로 사용하기 편하죠.

또한 CSP 문제 해결법은 탐색 공간에서 많은 견본(Swatch)을 빠르게 제거하기 때문에 상태 공간 탐색법보다

훨씬 빠른 속도를 보여줄 수 있습니다. 예를 들어 우리가 위 문제에서 SA = BLUE를 먼저 선택했다면

빠르게 인접한 5개 도시들의 값에서 BLUE를 빠르게 제거할 수 있습니다.

제약 전파의 이점이 없다면 탐색 절차는 총 3^5 = 243개의 배열을 전부 뒤져봐야 할 것입니다.

하지만 우리는 이러한 제약의 전파를 이용해서 BLUE를 한 번 제거하면 다시는 고려할 필요가 없어지죠.

결과적으로 2^5 = 32개의 배열만을 보아도 되는 것입니다. 전체에서 13%만 확인하면 될 정도로 줄었죠.

일반적인 상태 공간 탐색에서 우리는 오직 구체적인 상태가 목표 상태인지만 확인하면 됩니다.

만약에 아니라면 다른 것을 제시하면서 목표 상태인지 확인해봅니다. 하지만 CSP에서는 반대로

해가 될 수 없는 요소들을 제거해버리면서 목표 상태가 될 수 밖에 없는 것들로 찾아냅니다.

즉, 부분적인 배열이 해가 아니라는 것을 이해하면 그 부분적인 배열과 비슷한 개선 요소(Refinement)를

제거해버림으로써 그 배열과 관련된 것들을 배제시켜버립니다.

즉, 정답에 가까운 것만 가져가겠다는 소리이죠.

게다가, 우리는 왜 배열이 해가 아닌지를 봄으로써

(제약 조건을 위반하는 변수들을 체크 함으로써)

문제가 되는 변수들에 더욱 집중을 할 수 있게 되는 것이죠.

결과적으로 아주 다루기 힘든 일반적인 상태 공간 탐색도 CSP로 공식화가 되면

아주 빠르게 해결이 가능해집니다.

6.1.2 Example problem : Job-shop Scheduling

< Job-Shop Scheduling >

다음의 예시로는 Job-Shop Scheduling을 들 수 있습니다.

공장들은 스케줄링의 문제를 가지고 있습니다. 공정화를 하는데 어떤 순서로 할 지 등에 관한 공정은

제약 조건을 이용해 나타낼 수 있고, 결과적으로 실제로 많은 문제들은 CSP 기술로 해결이 된다고 합니다.

차를 조립하는 스케줄링에 관한 문제를 고려해봅시다.

전체적인 일은 임무들의 연속으로 이루어지겠습니다. 이 때

각각의 변수의 값은 임무가 시작되는 시간이라고 가정하겠습니다.

제약 조건은 어떠한 임무는 반드시 특정한 임무의 다음에 시행이 되어야한다는 것이죠.

쉽게 말해서, 차 공정에 있어서 확실한 순서가 있다는 소리입니다.

차 바퀴는 반드시 휠 캡이 올려지기 전에 만들어져야하겠죠. 이러한 순서를 CSP를 이용해 정하겠다는 것입니다.

이러한 제약 조건들은 또한 완성이 되기 위해서 얼마나 많은 시간이 임무에 필요한지 구체화해줍니다.

차 공정의 일부분만 한 번 고려해보겠습니다. 총 15가지 임무가 있다고 생각합시다.

엑셀 만들기(앞, 뒤), 휠 붙이기(앞, 뒤, 왼, 오), 휠에 너트 부착(앞, 뒤, 왼, 오), 휠 캡 붙이기(앞, 뒤, 왼, 오), 점검하기

이렇게 총 2 + 4 + 4 + 4 + 1 = 15개의 임무가 있다고 가정할 수 있겠지요.

이것들을 전부 각각 하나의 변수라고 생각합시다.

따라서, X = { AxleF, AxleB, WheelRF, WheelLF, WheelRB, WheelLB,

NutsRF, NutsLF, NutsRB, NutsLB, CapRF, CapLF, CapRB, CapLB, Inspect }

이렇게 정의를 내릴 수 있겠습니다.

각각의 변수에 대한 값은 이 임무가 시작되는 시간이라고 가정합니다.

이 다음에 우리는 우선 제약(Precedence Constraints)을 나타내야겠습니다.

이 우선 제약은 각각의 임무 사이에 적용되는 것입니다. 그냥 말 그대로 우선 순위 제약이겠죠.

만약에 T1가 T2가 이루어지기 전에 우선되어야 할 뿐 아니라 T1가 D1 만큼의 시간을 소요한다면

제약은 다음과 같이 적을 수 있겠습니다. T1 + D1 <= T2

또한 예를 들어 휠이 만들어지기 전에 반드시 엑셀이 놓여져야만 하고

엑셀을 만들어 부착하는 데 10분의 시간이 소요된다고 가정을 한다면 다음과 같이 쓸 수 있겠죠.

AxleF + 10 <= WheelRF; AxleF + 10 <= WheelLF;

AxleB + 10 <= WheelRB; AxleB + 10 <= WheelLB;

또한 각각의 휠이 부착되고(1분 소요) 너트로 고정이 되어야하고(2분 소요) 그 뒤에

휠 캡이 붙여져야 한다면 다음과 같이 쓸 수 있습니다.

WheelRF + 1 <= NutsRF; NutsRF + 2 <= CapRF;

WheelLF + 1 <= NutsLF; NutsLF + 2 <= CapLF;

WheelRB + 1 <= NutsRB; NutsRB + 2 <= CapRB;

WheelLB + 1 <= NutsLB; NutsLB + 2 <= CapLB;

만약에 휠을 만들어 부착하는데 4명의 엔지니어가 필요하고

그들은 오직 하나의 툴을 공유한다면 이 때 분리성 제약(Disjunctive Constraint)가 필요할 수 있습니다.

쉽게 말하자면 AxleF와 AxleB는 동시에 만들어지는 것이 아닌 것입니다.

예를 들면 다음과 같죠. AxleF + 10 <= AxleB 혹은 AxleB + 10 <= AxleF와 같이 표현할 수 있습니다.

이것은 굉장히 논리적 수학적 연산이 가미된 복잡한 제약처럼 보일 수 있습니다.

하지만 이것도 단순히 AxleF와 AxleF가 가질 수 있는 값의 제약일 뿐입니다.

또한 우리는 최후의 점검이 결과적으로 3분을 필요로 한다고 생각할 수 있겠죠.

모든 변수는 결과적으로 점검(Inspect)를 제외하고 X + Dx <= Inspect라는 제약 조건을

가지게 될 수 있는 것입니다. 마침내 우리는 모든 조립 공정이 30분을 필요로한다는 것을

알 수 있습니다. 우리는 결과적으로 모든 변수의 영역을 다음과 같이 정할 수 있습니다.

Di = { 1, 2, 3, ..., 27 }

아까 말했듯이 변수의 값은 각각의 임무(과정)이 시작되는 순간입니다.

예상대로라면 조립 공정이 시작이 되고 27분이 되기 전에 휠 캡까지 씌워진 뒤에

27분에 정확히 점검이 시작되서 3분 뒤에 끝나겠죠.

결과적으로 변수의 값은 1부터 27까지의 수가 될 수 있는 것입니다.

하지만 실제로 이러한 조립 공정에 쓰이는 변수는 수 천, 수 만 가지라는 것을 알아야 합니다.

실제로는 아주 복잡하게 쓰이죠. 여기서는 아주 간단하게 풀었지만요.

또한 몇몇 경우에서는 훨씬 복잡한 제약들이 CSP 공식화를 어렵게 만들어냅니다.

인공지능 서적의 거의 끝 부분에서는 그러한 부분을 해결해 줄 최고로 멋진 진보된 방법을

알려주는데 아마 대부분의 학부생은 거기까지 배우지 않을 듯 합니다.

6.1.3 Variations on the CSP Formalism

< Variations on the CSP Formalism >

일반적으로 CSP에 쓰이는 변수들은 ?이산적(Discrete)하고 유한한 영역(Finite Domain)을 가지고 있습니다.

맵 색칠하기 문제나 스케줄링 문제와 같은 경우도 위와 같은 특징을 가지고 시간 제한도 가지고 있죠.

정말 간단한 예시로 8-Queens 문제를 들 수 있죠. 예를 들면 8-Queens에서는 각각의 열 마다 하나의

변수인 퀸을 가지고 있다고 할 수 있고 이 퀸들은 영역은 { 1, 2, 3, 4, 5, 6, 7, 8 }이 되겠습니다.

이산적인 영역은 유한하다고 할 수 있습니다. 사실 아까 다룬 예제들도 전부 변수들의 값 제한이 있다고 할 수 있죠.

만약 무한한 영역이라면 모든 가능한 값들의 조합을 나열함으로써 제약을 묘사하기 어렵겠죠

대신에 제약 언어(Constraint Language)는 T1 + D1 <= T2와 같이 쓰일 수 있으므로

반드시 제약 조건을 이해시키기 위해서 사용될 필요가 있겠습니다.

왜냐하면 이렇게 되면 모든 T1과 T2의 값을 (T1, T2)의 형태로 전부 나열할 필요가 없게 되니까요.

특별한 알고리즘 해결은 정수 변수에 선형적인 제약(Linear Constraint)을 걸 수 있습니다.

선형 제약(Linear Constraint)는 '어떤 변수들의 값에 부과된 일차식의 제약'을 의미합니다.

이러한 경우는 일반적인 비선형 제약으로는 문제를 해결할 수 없는 것으로 보일 수 있죠.

연속적인 영역(Continuous Domains)의 제약 만족 문제는 현실 세계에서 아주 일반적입니다.

또한 실제 여러 연구의 영역에서 넓게 다루어지고 있기도 합니다. 예를 들어 설명하자면,

허플 우주 망원경의 연구 스케줄링은 연구에서 굉장히 정밀한 측정 시간을 요구합니다.

각각의 관찰에서 시작과 끝 그리고 전략은 연속적인 값의 변수들입니다.

이러한 값들은 또한 천문학적인, 선행되고 아주 강력한 제약 조건에 복종해야합니다.

?아주 잘 알려진 연속적인 CSP의 카테고리로는 선형 프로그래밍(Linear Programming) 문제가 있죠.

?이 선형 프로그래밍에서는 제약 조건들은 반드시 선형적인 측면에서 일치하거나 불일치해야 합니다.

선형 프로그래밍 문제는 다항식의 변수들의 값으로 해결이 됩니다.

여기서도 아주 다양한 프로그래밍 예제들이 있습니다.

또한 다양한 진법들의 제약이 있을 수 있습니다.

?Unary Constraint(1진법의 제약) : <(SA), SA != GREEN>

Binary Constraint(2진법의 제약) : SA != NSW

High-Order Constraint(고차적 제약) : BETWEEN(X, Y, Z) -> Y는 X와 Z 사이의 값이다.

Global Constraint : 임의적인 변수 값을 포함하는 제약

일반적인 Global Constraint를 Alldiff라고 합니다.

모든 변수들은 각각 다른 값을 가져야만 한다는 제약을 가지고 있죠.

Alldiff가 아마 All Difference라는 뜻을 가지고 있는 것 같습니다.

예를 들어 스도쿠 퍼즐에서는 하나의 열 혹은 하나의 행의 값들은

이 Alldiff 제약을 만족시켜야만 하죠.

?또 다른 예시로는 복면산(Cryptarithmetic) 퍼즐이 있을 수 있습니다.

이 복면산 퍼즐은 많이 유명하기 때문에 설명을 생략하겠습니다.

예를 들어 다음과 같이 Alldiff(F, T, U, W, R, O)라는 Global Constraint가 주어져있다고 한다면

다음의 n-ary constraints로 퍼즐의 네가지 열들을 적어볼 수 있겠습니다.

O + O = R + 10 * C10

C10 + W + W = U + 10 * C100

C100 + T + T = O + 10 * C1000

C1000 = F

C10, C100, C1000는 보조 변수라고 할 수 있습니다.

이 변수들은 10, 100, 1000 열로 이행되는 값들이죠.

즉, 더해져서 올라가는 값을 말합니다.

이러한 제약 조건들은 제약 하이퍼그래프(Constraint Hypergraph)로 나타낼 수 있습니다.

그림 (b)를 보시면 아실 수 있죠. 하이퍼그래프는 일반적인 노드(동그라미)와 하이퍼 노드(사각)로 구성됩니다.