기초 인공지능 11

TonyHan·2020년 10월 16일

20) 기초인공지능

목록 보기

11/21

7. Logical Agents

사람은 여러가지의 지식을 가지고 있습니다. 그리고 그러한 지식을 표현(representation)할때 문장(sentence)를 사용합니다. 당연히 그러한 문장은 무의미하지 않습니다. 즉, 인간은 무언가에 대한 반응으로 단순한 반사 작용의 메커니즘이 아니라 자신이 가지고 있는 지식의 내부 표현들에 작용하는 추론(reasoning) 공정들로 달성됩니다.

인공지능에서는 지식 기반 에이전트(knowledge-based agent)라는 것은 지능에 대한 위와 같은 접근방식을 포함하는 것을 말합니다.

부분 관찰 가능 환경(partially observable)에서 에이전트가 현재 상태에 관해 아는 것을 표현하는 유일한 방식은, 모든 가능한 구체적 상태들을 단순하게 나열하는 것일 뿐입니다. 커다란 환경에서는, 실제 환경에서는 그러한 표현 방식이 비현실적일 확률이 아주 높습니다.

따라서 '논리적 에이전트'에서는 복잡한 세계의 표현을 형성할 수 있고 추리 공정을 이용해서 세계에 대한 새로운 표현들을 유도할 수 있으며 그러한 새 표현들을 이용해서 다음에 할 일을 연역할 수 있는 에이전트를 설계할 수 있도록 공부합니다.

즉, 논리(logic)를 지식 기반 에이전트가 가능한 표현들의 일반적 부류(class)로 취급하고 그러한 에이전트는 정보를 다양한 목적에 맞게 조합 및 재조합할 수 있게 됩니다.

7.1 Knowledge-based Agents

지식 기반 에이전트의 핵심 구성요소는 기본의 지식 베이스, 지식 기지(knowledge base)라고 불리는 것 입니다.

이러한 지식 기지는 문장들의 집합입니다. (Knowledge base is set of sentences in a formal language) 여기서 '문장'이라는 것은 기술 용어입니다.

기본적으로 지식 기지라는 것에 새로운 문장, 즉 새로운 지식을 추가하는 방법과 지식 기지에 있는 문장을 질의하는 방법이 필요합니다. 이때, 새로운 문장을 추가하는 방법을 TELL이라 말하며 지식 기지에 있는 문장을 질의하는 방법을 ASK라고 합니다. 그리고 두 연산의 과정 속에는 추리(inference), 즉 기존의 문장들에서 새로운 문장을 이끌어 내는 공정이 존재합니다.

추리라는 것은 누군가가 ASK 연산을 수행했을때 그에 대한 답이 반드시 과거에 지식 기지에 TELL 연산을 통해 추가된 어떠한 지식(문장)에서 도출되어야 한다는 요구조건을 만족해야 합니다. 다시 말해 추리의 공정이 근거 없이 말을 꾸며내는 것이 되면안된다는 것 입니다.

아래의 사진은 지식 기반 에이전트 프로그램의 기본적인 큰 틀입니다. 해당 에이전트는 지각 하나를 입력받고 동작 하나를 반환합니다. 그리고 에이전트는 지식 기지(KB)를 유지하고 있습니다. 그리고 에이전트는 사전에 자신의 지식 기지에 일정한 배경 지식(background knowledge)를 가지고 있을 수 있습니다.

TELL(KB, MAKE-PERCEPT-SENTENCE(percept, t)) 에서는 주변의 환경을 지각하여(percept) 지식 기지(KB)에 알려주는 TELL연산을 수행합니다. 그리고 지식 기지에 행동(action)을 요청하는 ASK 연산을 수행하고 자신이 선택한 행동을 다시 지식 기지에 알려주는 TELL연산을 수행한 후에 행동을 반환합니다.

위에서 알아본 TELL과 ASK 연산의 정의를 생각해본다면 지식 기반 에이전트는 단순히 특정 동작들을 계산을 통해 도출해내는 프로그램이 아닙니다. 지식 기반 에이전트는 지식 수준(knowledge level)에서의 서술, 정의를 준수합니다. 위에서 언급했듯이 특정한 지식을 통한 근거있는 행동만을 반환하는 것 입니다.

이러한 수준에서 개발자는 에이전트가 현재 알고 있는 것과 에이전트의 목표를 결정해준다면 에이전트의 행동을 바로잡고 예측할 수 있습니다.

예를 들어서 A장소에서 B장소로 가는 것이 목표인 에이전트가 있는데 두 장소를 연결하는 유일한 경로 p라는 것을 에이전트가 알고 있다고 가정하겠습니다. 그렇다면 개발자는 에이전트가 p라는 경로를 통해 움직일 것을 충분히 예상할 수 있습니다. 그것이 에이전트 자신이 목표를 달성하는 유일한 방법임을 자신의 지식 기지에서 도출해 낼 수 있기 때문입니다.

개발자는 에이전트가 알아야 할, 가져야 할 지식을 단순히 TELL연산으로 알려주는 방법으로 하여금 프로그램을 설계할 수 있습니다. 즉 에어전트의 지식 기지가 비어있는 상태에서 에이전트가 주어진 환경에서 적절하게 행동을 반환할 수 있을 때 까지 문장(지식)들을 TELL 연산으로 하나씩 주입할 수 있는 것 입니다. 그리고 이것을 선언적(Declarative) 시스템 구축 접근방식이라고 부릅니다. 또한, 이와 다르게 절차적(procedural) 시스템 구축 접근방식이 존재합니다. 절차적 접근방식은 바람직한 행동을 프로그램 코드에 직접 입력합니다.

그리고 현재에 있어서는 성공적인 에이전트의 설계에 선언적 요소와 절차적 요소가 모두 들어 있는 경우가 많다는 점과 선언적 지식을 좀 더 효율적인 절차적 코드 안에 조합해 넣을 수 있는 경우가 많다는 점이 알려져 있습니다.

7.2 The Wumpus World

이번엔 위에서 학습한 내용들을 바탕으로, 지식 기반 에이전트의 가치를 볼 수 있는 웜푸스 세계(Wumpus world)라는 환경을 살펴보겠습니다.

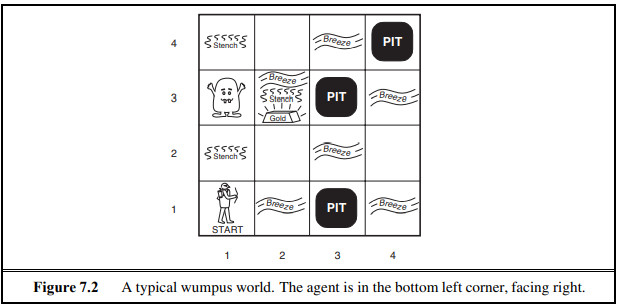
위와 같은 웜푸스 세계에 대해 간략히 설명한다면, 웜푸스 세계는 여러 개의 방이 통로로 연결된 동굴입니다. 동굴 어딘가에는 거대한 괴물인 웜푸스가 존재합니다. 그림을 보면 1열 3행에 존재함을 알 수 있습니다. 웜푸스를 만나면 에이전트는 사망하게 됩니다. 에이전트는 웜푸스를 화살로 쏴서 죽일 수 있지만 화살은 딱 하나만 존재합니다. 그리고 특정 방에는 바닥이 없는 구덩이(pit)이 존재합니다. 구덩이가 존재하는 방에 들어가면 마찬가지로 에이전트가 죽게됩니다. 그리고 금 더미가 놓인 방이 있습니다. 이를 정리해 보면 웜푸스 세계에 존재하는 요소는 웜푸스, 구덩이, 금으로 총 3가지 입니다.

각각의 요소는 특징을 가지고 있습니다. 그림을 보면 확인 할 수 있듯이 웜푸스가 존재하는 방에 인접한 방은 악취(stench)가 존재하고, 구덩이가 존재하는 방에 인접한 방은 미풍(breeze)이 존재하며, 금이 존재하는 방에는 반짝임(glitter)이 존재합니다.

이러한 환경에 처한 에이전트의 주된 난제는, 초기에 환경의 구성에 대해 전혀 무지하다는 것 입니다. 이러한 무지를 극복하기 위해서는 에이전트에게 추론이 필요합니다.

7.3 Logic

이번에는 논리적 표현과 추론의 근본 개념들을 소개합니다.

지난 포스팅에서 지식 기지에 대해서 알아보았습니다. 그리고 지식 기지는 문장들로 구성된다고 하였습니다. 여기서 문장들은 표현 언어의 구문(Syntax)을 따릅니다. 표현 언어의 구문은 적격(well-formed)인 문장을 규정합니다. 쉽게 말해서 구문은, 문장을 만드는 규칙을 말합니다. 예를 들어, "x+y=1"이라는 문장은 적격이지만 "+x1y="은 적격이지 않습니다.

논리는 문장의 의미론(Semantics), 즉 문장의 뜻도 함께 정의해야 합니다. 의미론은 각각의 가능한 세계(possible world)에 대한 문장의 진리(truth: 참 또는 거짓)를 정의합니다. 예를 들어 "x+y=2"라는 문장은 x가 1이고 y가 1인 세계에서 참이지만 x가 1이고 y가 0인 세계에서는 거짓입니다. 표준적인 논리에서 모든 문장은 각각의 가능한 세계에서 진리를 표현, 즉 참 또는 거짓이어야 합니다. 참도 아니고 거짓도 아닌 애매한 문장은 존재하지 않습니다. 아래의 예시들로 다시 한번 정리할 수 있습니다.

'x + 2 >= y' is a sentence; x2+y>= is not sentence
'x + 2 >= y' is true iff the number x + 2 is no less than the number y
'x + 2 >= y' is true in a world where x=7, y=1
'x + 2 >= y' is false in a world where x=0, y=6

이제 추론에 대해서 다루어 보도록 하겠습니다. 논리적 추론에서는 위에서 알아본 문장들 사이의 논리적 함축(entailment) 관계가 관여합니다.

함축이란, 한 문장이 다른 문장을 '논리적으로 따른다(follow)'는 개념을 나타내는 용어입니다. 함축은 아래와 같은 표기법으로 나타낼 수 있습니다.

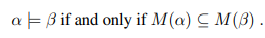
이는 모든 문장 (이후 a라고 표기)가 문장 (이후 b라고 표기)를 함축한다는 뜻 입니다.

함축이란 용어의 형식적인 정의는 다음과 같습니다. 만일 a가 참인 모든 가능한 세계에서 b 역시 참일때에만 a|=b 이다.

즉 위의 표기법에서 a가 b 보다 더 강한 문장입니다.

이러한 함축이라는 개념을 웜푸스 세계의 예제에도 적용할 수 있습니다.
에이전트는 (1,1)의 방에서는 아무것도 감지하지 못했지만 (2,1)에서는 미풍을 감지하였습니다. 이러한 지각들과 웜푸스 세계의 규칙들에 대한 에이전트의 지식이 합쳐져서 에이전트의 지식 기지를 형성합니다. 에이전트 입장에서는 (1,2)와 (2,2), (3,1)에 구덩이가 있는지가 관심의 대상입니다. 그 세칸에는 각각 구덩이가 존재하는지 존재하지 않는지의 경우가 존재하므로 가능한 세계의 수는 2의 3승, 총 8개 입니다. 이러한 세계를 도형으로 나타내면 아래와 같습니다.

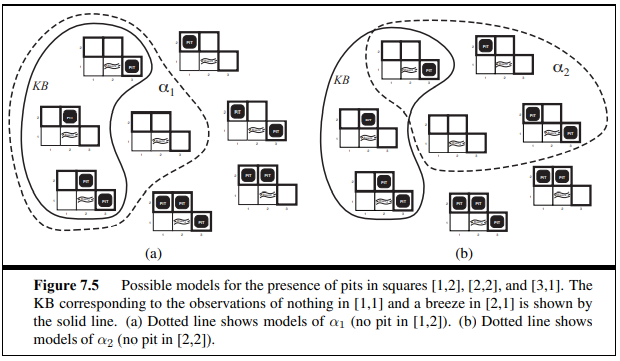
위의 그림에서 각각의 선이 의미하는 바는 다음과 같습니다.

KB = 에이전트가 가지고 있는 지식 기반 = "(1,2)에 구덩이가 없다." (이후 a1 이라고 표기) = "(2,2)에 구덩이가 없다." (이후 a2 라고 표기)

a1이 가능한 세계들과 a2가 가능한 세계들이 위의 그림에 표현되어 있습니다.

이들로 부터 우리는 다음과 같은 사실을 알 수 있습니다.

KB가 참인 모든 가능한 세계에서 a1도 참이다.

따라서 KB|=a1 입니다. 즉 (1,2)에는 구덩이가 없습니다. 또한 다음과 같은 사실도 알 수 있습니다.

KB가 참인 가능한 세계중 a2가 거짓인 가능한 세계들이 존재한다.

따라서 KB|=a2가 아닙니다. 즉 에이전트는 (2,2)에 구덩이가 없다는 사실을 도출할 수 없습니다. 마찬가지로 (2,2)에 구덩이가 있다는 사실 또한 도출할 수 없습니다.

이러한 예시는 함축관계를 보여줄 뿐만 아니라, 함축의 정의를 이용해서 결론을 이끌어 내는 방법, 즉 논리적 추리를 수행하는 방법 또한 보여줍니다.

함축과 추리의 이해에 도움이 되기 위해 KB의 모든 결과의 집합이 건초 더미이고 a가 하나의 바늘이라고 생각하면, 함축은 건초 더미에 바늘이 존재한다는 것에 해당하고, 추리는 그 바늘을 찾는 것에 해당합니다.

이러한 구분을 형식적 표기법으로 나타낼 수 있습니다.

추리 알고리즘 i가 KB로부터 a를 도출할 수 있을 때, 이를

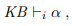
로 표현할 수 있습니다. 이것은 'a가 i에 의해 KB로부터 유도된다' 또는 'i는 KB로부터 a를 유도한다'로 말 합니다.

함축된 문장들만 유도하는 추리 알고리즘을 가리켜 건전한(sound) 또는 진리를 보존하는(true-preserving) 알고리즘이라고 말합니다. 반대로 생각해본다면, 건전하지 않은 추리 절차는 추리과정에서 무언가를 근거 없이 만들어 냅니다.

완결성(completencess) 역시 바람직한 속성입니다. 함축된 임의의 문장을 유도할 수 있는 추리 알고리즘은 완결적 입니다. 실제 건초 더미의 경우 지푸라기들을 체계적으로 조사한다면 그 건초 더미에 바늘이 있는지의 여부를 항상 결정할 수 있음이 명핵합니다. 그러나 지식 기지 중에는 결과들의 건초 더미가 무한한 것들이 많기 때문에 완결성이 중요한 문제가 됩니다. 다행히, 여러 지식 기지를 다루기에 충분한 표현력을 가진 완결적인 논리적 추리 절차들이 많이 있습니다.

지금까지 전제들이 참인 세계에 대해서는 결론이 반드시 참인 추론 공정을 알아보았습니다.

정리하자면, 만일 실제 세계에서 KB가 참이면, 건전한 추리 절차를 이용해서 KB로부터 유도한 임의의 문장 a도 실제 세계에서 참입니다.

앞서 논리에 대한 이야기를 진행하면서 '가능한 세계'라는 표현을 많이 사용하였습니다. 헌데, 좀 더 엄밀한 정의가 필요할 때 '가능한 세계'대신 '모형(Model)'이라는 용어를 사용합니다.

가능한 세계는 에이전트가 처할 수도 있고 그렇지 않을 수도 있는, 잠재적인 실제 환경이라고 생각할 수 있는 반면, 모형은 수학적인 추상입니다. 각각의 모형은 그냥 모든 유관한 문장의 참 또는 거짓을 고정시킨 것입니다.

문장 a가 모형 m에서 참일 떄, 이를 'm이 a를 만족한다'라고 말할 수 있습니다. 때에 따라서는 'm이 a의 모형이다'라고 말할 수도 있습니다. 또한 a의 모든 모형의 집합을 M(a)로 표기합니다.

7.4 Propositional Logic : A Very Simple Logic

7.4.1 Syntax

명제 논리의 구문(syntax)은 허용되는 문장들을 정의합니다. 즉, 어떻게 문장을 구성해야 하는지를 이야기합니다.

하나의 문장, 원자적 문장(atomic sentence)은 하나의 명제 기호(proposition symbol)로 구성됩니다. 그리고 그러한 기호는 참(true)이거나 거짓(false)인 하나의 명제를 나타 냅니다. 예를 들어 P, Q, R, North 등이 명제 기호입니다.

이때, 항상 고정적 의미를 가진 명제가 있는데 자주 보셨듯이 True와 False 입니다. True는 항상 참인 명제이며 False는 항상 거짓인 명제입니다.

또한 우리는 간단한 문장들을 괄호와 논리 접속사(logical connective)로 연결해서 복합 문장을 만들 수 있습니다.

일반적인 접속사(연산자)는 아래와 같습니다.

7.4.2 Semantics

명제 논리의 구문을 살펴보았으니, 이제 명제 논리의 의미론을 살펴보도록 하겠습니다.

의미론(semantics)이란 특정 모형에 대한 문장의 진리를 결정하는 규칙들을 정의합니다. 명제 논리에서 모형은 모든 명제 기호의 진릿값(truth value), 즉 참(true) 또는 거짓(false)을 고정하는 역할만 합니다.

명제 논리의 의미론은 주어진 모형에 대해 임의의 문장의 진릿값을 계산하는 방법을 명시해야 합니다. 모든 문장은 원자적 문장과 위에서 본 다섯가지 접속사로 구성됩니다. 따라서 원자적 문장의 진릿값을 계산하는 방법과 각 접속사로 만들어지는 문장의 진릿값을 계산하는 방법을 명시해야 합니다.

원자적 문장에 대한 의미론은 다음과 같습니다.

True는 모든 모형에서 참이고 False는 모든 모형에서 거짓이다.
다른 모든 명제 기호의 진릿값은 반드시 모형 자체에 명시되어 있어야 한다.

복합 문장에 대해서는 다섯 가지 규칙이 존재합니다.

이러한 규칙들은 임의의 모형 m 안의 임의의 문장 P와 Q에 대해 성립합니다.

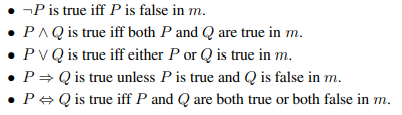
이는 또한 진리표로 표현이 가능합니다.
이러한 표를 이용하면 임의의 모형 m에 대한 임의의 문장 s의 진릿값을 간단한 재귀적 평가를 통해서 구할 수 있습니다.

7.4.4 A simple inference procedure

아래는 표준적인 논리 동치 관계들을 나타내는 것으로써 각각의 문장들로 인한 복합문장들의 참 또는 거짓을 구별할 때 사용됩니다.

7.5 Propositional Theorem Proving

리는 모든 모형들을 열거하면서 문장이 모든 모형에서 성립하는지 점검하는 모형 점검 방식에 대해 알아보았습니다. 이제는 정리 증명(Theorem proving)을 이용하여 함축 관계를 확인하는 방법에 대해서 알아보겠습니다. 우리가 앞으로 알아볼 접근 방식에서는 주어진 문장의 증명을 구축하여 함축관계를 확인하기 위해서 지식 기지(KB)에 있는 문장들에 여러가지 추리 규칙들을 적용할 것 입니다. 우리가 앞에서 살펴본 모형 점검 방식에 비해, 모형이 많을 수록 또는 정리 증명의 내용이 짧을 수록 보다 효율적인 증명 알고리즘이 될 것입니다.