8. First-Order Logic

우리는 지난 시간에서 명제논리를 사용하여 지식 기반 에이전트가 자신이 속한 세계를 표현하는 방법과 다음에 취할 동작을 연역하는 방법을 살펴보았습니다. 하지만 명제논리는 복잡한 환경에 대한 지식을 간결하게 나타내기에는 표현력이 너무 약합니다. 따라서 우리는 이번 포스팅 부터하여 우리가 가진 상식의 상당 부분을 표현하기에 충분한 표현력을 가진 1차 논리(first-order logic)에 대해서 살펴보겠습니다.

8.1. Representation Revisited

8.1.1. The language of thought

생각의 언어가 first-order logic으로 간주한다. 일반적인 언어는 사람은 표현력이 좋아 금방 이해하지만 자연어나 서술들은 사람은 그게 무슨언어인지 바로 이해한다 하더라도 AI 언어인 first-order logic으로 표현할 수 있는 것은 아님. 하지만 여기에서의 logic은 어떠한 logic으로 표시되었다고 할때 그 언어속에서 어떤식으로 reasoning 추론하고 결론을 내는 과정은 사람의 머릿속에서 사고해 나가지만 AI에서는 이것을 저절로 사고하게 하는 것은 어렵거나 불가능하기 때문에 표현된 자연어를 first-order logic으로 표현 한다음에 앞 단원의 logic machanism과 reasoning 모두, influence rule을 가지고 우리가 원하는 정보나 지식을 검색하고 기록하고 추론한다.

8.1.2. Combining the best of formal and natural languages

1차 논리에서는 명제 논리의 장점, 문맥 독립적이고 모호하지 않은 선언적, 조합적 의미론을 기반으로 삼고 자연어의 단점들은 제외하고 표현력이 큰 착안들만 가져왔습니다.

1차 논리에서는 다음과 같은 것들을 포함합니다.

• 객체(Objects): 사람, 집, 수, 이론, 색, 야구, 전쟁, 세기, ...
• 관계(Relations): 빨갛다. 둥글다, 가짜, 다층, ... / 형제이다, ~보다 크다, ~안에, ~의 일부, ...
• 함수(Functions): ~의 아버지, ~의 절친, ~보다 하나 많다, ~의 시작, ...

1차논리의 언어는 객체들과 관계들을 중심으로 구축됩니다.

명제 논리와 1차 논리의 주된 차이점은 두 언어의 존재론적 함의(ontological commitment)사이에 놓여 있습니다. 즉, 둘은 현실의 본성에 대해 무엇을 가정하는지와 관련해서 크게 다릅니다.
명제 논리에서는 어떤 세계에서 성립하거나 성립하지 않는(그러나 둘 다는 아닌) 사실들이 존재합니다.
하지만 1차 논리는 더 많은 것을 가정합니다. 구체적으로, 1차 논리는 객체들로 세상이 구성되며 그 객체들 사이에는 성립하거나 성립하지 않는 관계들이 있습니다.

논리들을 인식론적 함의(epistemological)로써도 바라볼 수 있습니다.
이는 각 사실에 관해 허용되는 가능한 지식 상태가 얼마나 많은지에 관련된 것입니다. 명제논리와 1차 논리에서는 하나의 문장이 하나의 사실을 표현하며, 에이전트는 그 문장이 참이라고 믿거나 아니면 거짓이라고 믿거나 아니면 아무런 의견이 없습니다.
아래 표는 다섯가지 논리의 존재론적 함의와 인신론적 함의를 정리한 것입니다.

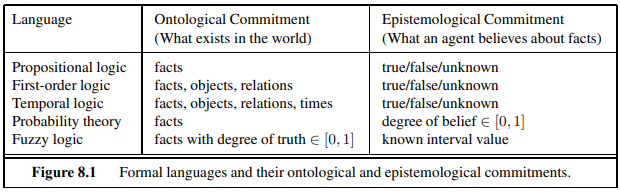
8.2. Syntax and Semantics of First-Order Logic

8.2.1 Models for first-order logic

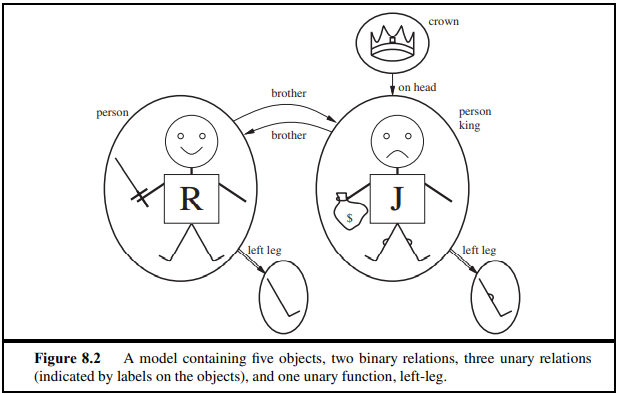
위의 예시는 왼쪽은 Richard 이고 오른쪽은 John 왕이다. 그래서 둘의 관게를 보면 John은 crown과의 관계는 crown이 John의 위에 있다. 반대로 Richard는 John의 형제이다. 만약에 여기 위에 아버지와 아들인 왕의 관계를 표현한다면 그 관계는 부모 자식의 관계를 가지게 된다.
그래서 실재 사례를 묘사하는 관계를 function이나 realation으로 표현하고자 한다.

8.2.2 Symbols and interpretations

위의 왕의 관계를 파악하고

위의 내용이 이전과 다른 것은 term이라는 것이 functinon(Trem...)이 되고 이는 맞물려서 출력 결과가 또 function에 들어가는 연쇄현상이 생기어남.

임의의 x 혹은 D에 속하는 y에 대해서 Man(x)라면 Has_leg 라는 식으로 표현한 것을 First-Order Logic이라고 볼 수 있음.

Qauntifier : 해당되는 모든 도메인의 element에 대해서 animal 일수도 있지만 딱 사람들의 집합인 도메인이라면 이건 할상 성립할 수 있으며 이때 정량자를 정한다. 그래서 ∀이것은 전체 정량자 ∃이것은 존재 정량자라고 한다.

8.2.4 Atomic senteces

위에서의 richard와 john의 관계를 syntex를 활용하여서 정리하고 있다.

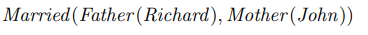
객체들을 지칭하는 항들과 관계들을 지칭하는 술어 기호들이 갖추어졌다면, 그 둘을 조합해서 원자적 문장(atomic sentences)를 만들 수 있습니다. 원자적 문장은 술어 기호가 반드시 하나 있어야 하며, 그 뒤에 괄호로 감싼 항들이 올 수도 있는 형태입니다. 원자적 문장의 인수가 복합항일수도 있습니다.

주어진 모형 안에서, 원자적 문장의 술어 기호가 지칭하는 관계가 그 인수들이 지칭하는 객체들 사이에서 성립하면 그 원자적 문장은 참입니다.

그리고 이러한 원자적 문장들을 논리 접속사들을 이용하여 좀 더 복합적인 문장을 만들 수 있습니다. 그리고 그러한 문장을 복합문장(complex sentences)이라고 합니다.

8.2.5 Complex sentences

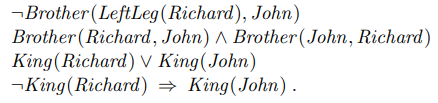
8.2.6 Quantifiers

Universal Qantification

어떤 논리가 객체들을 지원할 때, 객체들이 가진 속성을 그 객체들의 이름으로 일일이 열거하지 않고 간결하게 표현하는 용도로 한정사가 사용됩니다. 한정사에서는 크게 전칭 한정사(Universal quantification)과 존재(existential) 한정사가 존재합니다. 먼저 전칭 한정사에 대해서 살펴보겠습니다.

먼저 하나의 예시를 들어보겠습니다. 다음의 문장은, '모든 왕은 사람이다'를 의미합니다.

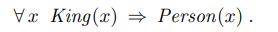
편의를 위해 전칭 한정사를 A로 표현하겠습니다.(원 표기는 위 문장의 표기가 맞습니다.)

보통의 경우 A는 "모든 ~에 대해"라고 읽습니다. 따라서 위의 문장은, "모든 x에 대해, 만일 x가 왕이면 x는 사람이다."라는 뜻입니다.

전칭 한정사의 경우 논리곱을 사용하는 데에 있어서 주의를 기울여야 합니다.

예를 들어, 책을 보는 사람은 모두 똑똑하다를 나타내면,

Ax readBook(x) => smart(x)

입니다. 하지만,

Ax readBook(x) ∧ smart(x)

와 같이 나타내면, 우리가 의도했던 바와 달리, 세상에 존재하는 모든 것이 smart 하게 됩니다.

다시말해, 아래의 문장은, 모든 사람은 책을 읽고 모든 사람은 똑똑하다라는 의미를 나타냅니다.

Existential Quantification

전칭 한정은 모든 객체에 대한 주장을 표현합니다. 이와 달리 존재 한정은 일부 객체들에 대한 주장을 표현합니다.

예들 들어 다음과 같이 사용됩니다.

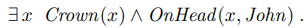
편의를 위해 존재 한정사를 E로 표현하겠습니다.(원 표기는 위 문장의 표기가 맞습니다.)

보통 Ex는 "~를 만족하는 x가 존재한다.'로 읽거나 "어떤 x에 대해 ~" 라고 읽습니다.

직관적으로 말해, Ex P 라는 문장은 P가 적어도 하나 이상의 x에 대해 참임을 말합니다.

존재 한정사에서도 주의할 점이 있습니다.

예를 들어, 책을 읽고, 똑똑한 누군가가 존재한다를 나타내면,

Ex readBook(x) ∧ smart(x)

입니다. 하지만,

Ex readBook(x) => smart(x)

와 같이 나타내면, 책을 읽는 누군가가 한명이라도 존재하면 문장이 참이 됩니다.