1단원
1.1.1 Total Turing test(나카마-크롬)
- natural language processing : 인간의 언어를 이해하고 처리할 수 있는 능력
- knowledge representation : 듣고 배운지식을 저장하고 표현할 수 있는 능력
- automated reasoning : 가지고 있는 정보나 지식을 이용해서 새로운 결론을 내거나 질문에 답하는 능력
- machine learning : 새로운 환경에 직면했을 때, 패턴을 탐지하고 추정해내는 능력
- Computer Vision : 물체를 인지하는 능력
- Robotics : 물체를 다루고 움직이는 능력
간단하게 기술하기
1.2.6 General-purpose search mechanism 에서 1.3.5 Knowledge-based Systems으로 변경된 배경 및 의미
배경 : General-purpose search algorithm은 너무 큰 크기의 문제등을 다루기에 어려움이 있었다. 모든 일반적인 경우에 대해 탐색하려하기 때문인데, 이를 weak method라 부른다.
해결책/의미 : 이를 해결하기 위해 domain-specific한 knowledge를 가진 system을 통해 특정 전문분야에 빈번히 일어나는 문제들을 처리할 수 있게 했는데, 이를 knowledge-based system이라 한다. 이 system은 기존에 축적된 지식체계를 바탕으로 문제가 주어졌을 때 최적의 해를 찾아 output으로 출력한다.
1.3.9 Intelligent agents 접근방식을 통해 얻어진 AI 연구의 두 가지 중요한 2가지 결과?
- 독립적으로 연구된던 subfield AI를 통합해 결과를 합칠 수 있게 됨
- 다른 분야(예 : 경제)와의 결합이 가능해짐
2단원
2.2.1 Rationality
rational agent의 정의가 무엇인지
1. 성공의 기준을 가진 수행 측정 결과
2. 에이전트의 환경에 대한 우선 지식
3. 에이전트가 수행할 수 있는 행동들
4. 에이전트가 연속된 날짜에 대해 인식하는 방법
2.3.1 Specifying the task environment - PEAS
시험문제는 디자인을 하였을때 다음의 대상이 될 수 있는 것을 적으면 됨
PEAS(Performance measure, Environment, Actuators, Sensors)
Performance : 얼마나 빠르고 안전하고 최소의 비용으로 목적지에 도착하는가(목표를 효과적으로 달성할 수 있나?)
Environment : 주변 환경에 대한 사전지식을 가지고 있는가?
Action : 목표를 달성하는데 적절한 행동을 하는가?
Sensor : 목표 달성에 필요한 정보를 효과적으로 인지할 수 있는가?
2.3.2 Properties of task environments(△)
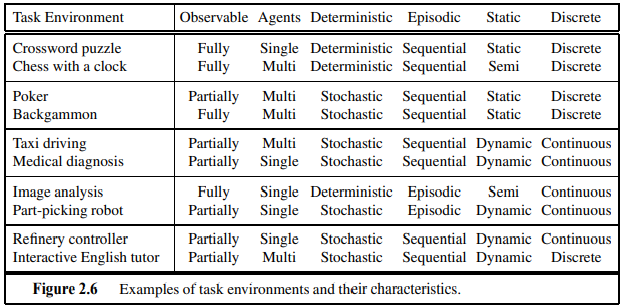
각 문제에 대해서 어떻게 처리되는지에 대해서 알아두면 좋음
2.4 The Structure of Agents
agents 총 5가지의 원리를 이해하고 설계를 외워야 함
2.4.2 Simple reflex agents
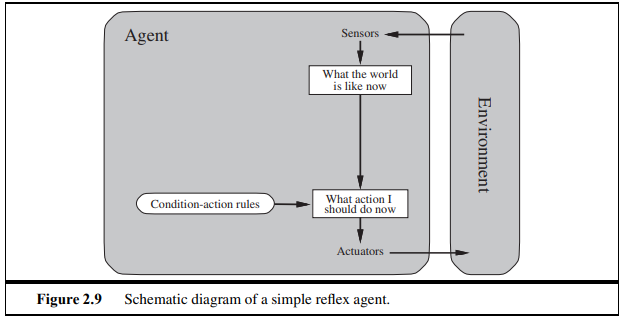
- 오직 current percept를 기본으로 행동
- 어떤 상태 정립을 위해 input이 들어오면 agent program 내에 보정된 연결 통해 행동
- 매우 제한적 지능, 사고력을 가짐
2.4.3 Model-based reflex agents
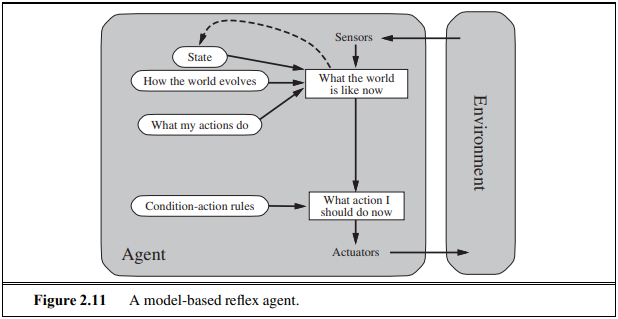
- agent가 percept history에 의존한 internal state를 갖고 있게 함으로써 현재 상태에서 관찰되지 않은 면에 대해 반응하도록 함
- "how the world works"에 대한 지식을 world의 "model"이라고 함
2.4.4 Goal based agents
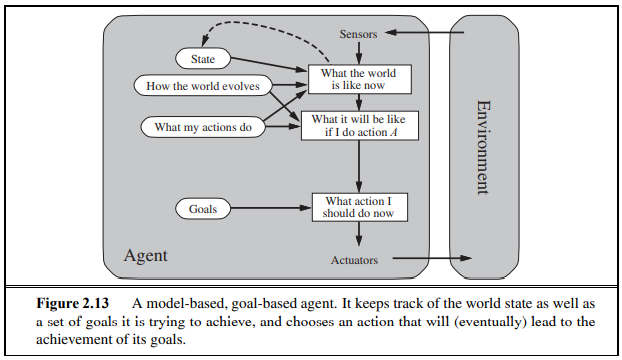
- 현재 상태 인지만으로 부족하기에 'goal information'이 필요함
- condition-action rule과는 다르게 미래에 대한 생각을 하지 않음
- 결정을 돕는 knowledge가 명시적으로 나타나 있고 수정 가능 -> flexible
2.4.5 Utility based agent
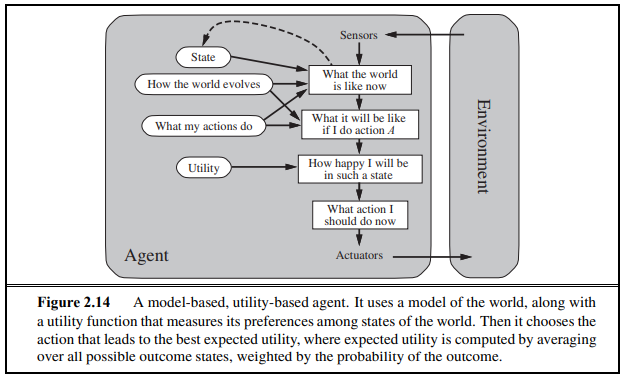
- 기존 agent들과는 달리 행복이라는 요소를 감안하여 가장 행복을 높게 가져올 수 있는 행동을 선택한다.
What the world is like now : 환경분석
What it will be like if I do action A : 행동결과예측
How happy I will be in such a state : 행복도 측정
What action I should do now : 행동결정
How the world evolves : 어떻게 환경이 변하는가
What my actions do : 나의 행동은 무엇인가
2.4.6 Learning agents
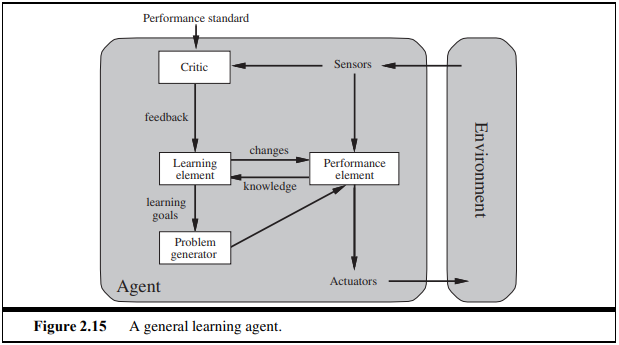
- sensor을 통해 인지한 문제를 해결하는 과정에서 기존에 가지고 있던 문제해결 절차보다 더 좋은 방안이 있다면 그에 맞는 해결 방안을 계속 학습해가며 더 나은 procedure로 나아가는 agent이다.
3장
3.2.2 Real-world problems(states, initial state, successor function, goal test, path cost들을 디자인 하시오)
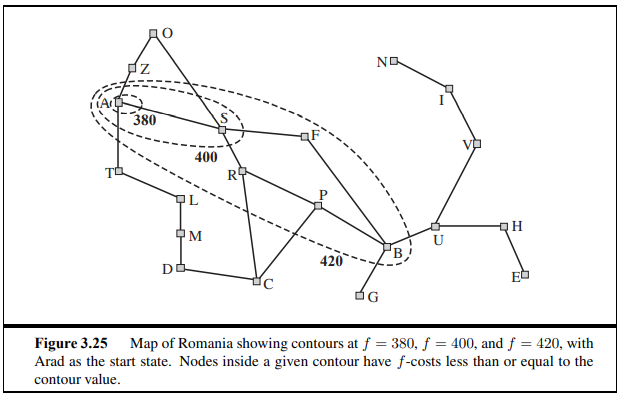
Vacuum World
State : location 2개, 더럽거나 안 더럽거나 = 2*(2^2) = 8가지
initial state : 어떠한 상태도 초기형태 가능
Action : Left, Right, Suck
Transition model : left는 왼쪽으로, right는 오른쪽으로 이동하고, suck은 더러운 물질을 빨아들이므로 clean state에서는 영향이 없다.
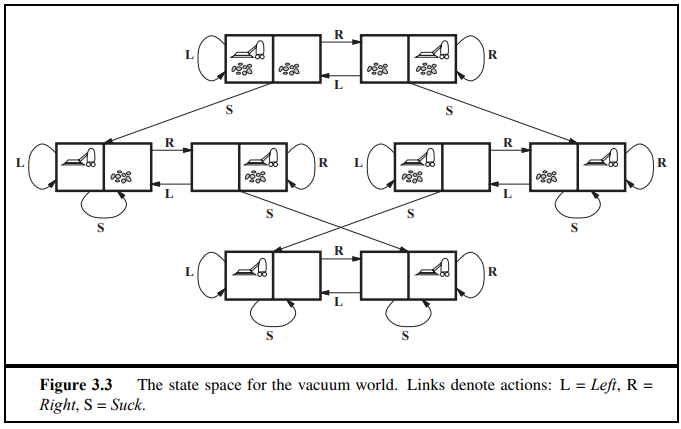
(이 문제에 대한 complete state space를 만드시오 문제)
Goal test : 모든 square들을 깨끗하게 만드는 것
Path cost : 한 step마다 1cost씩. 따라서 path cost는 총 step의 갯수
8-puzzle
state : 9개의 square안에 8개의 tile과 1개의 blank.
initial state : 어떠한 상태도 초기형태 가능
actions : 빈칸을 상하좌우로 움직이고, 빈칸과 움직인 방향에 있는 block과 자리를 바꿈
Transition model : state를 주고, 결과 state를 반환
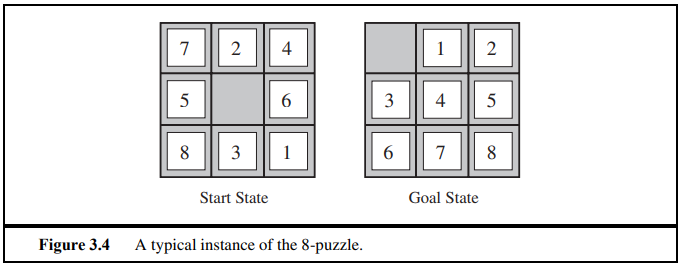
goal test : (12/345/678)과 같은 모양 그리기
path cost : 한 step마다 1 cost씩. 따라서 path cost는 총 step의 개수
3.3 Searching for Solutions

3.3.2 Measuring problem-solving performance
- Completeness : 해결책 제시를 보장해주는가?
- Optimality : 최적의 해를 찾아주는가?
- Time Complexity : 얼마나 오랜시간이 걸리는가?
- Space Complexity : 얼마나 많은 메모리를 차지하는가?
3.4 Uniformed Search Strategies
각 Search별 설명을 적고 진행방향도 작성
- Breath-first search
- 너비 우선 탐색, 같은 레벨의 node들을 먼저 탐색한다.
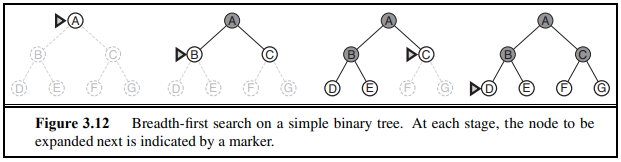
- Uniform-cost search
- BFS식으로 진행하면서 현재까지 왔던 node의 cost을 보고 가장 낮은 min-cost를 가진 node 부터 검색
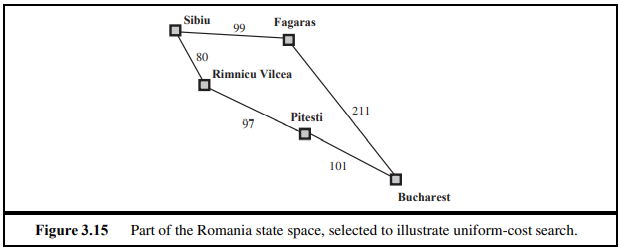
- Depth-first search
- 깊이 우선 탑색, 자식 노드들을 계속해서 확장해가면서 탐색한다.

- Depth-limited search
- DFS에서 depth가 너무 커지는 문제를 보완하기 위해 depth에서 limit를 정한다.
- Iterative deepening search
- BFS와 DFS를 결합한 형태로, DFS에서 limit를 점차적으로 늘려가는 방식입니다. 우리가 전체 상태 공간의 지름을 알지 못할때 이 방법이 훌륭함
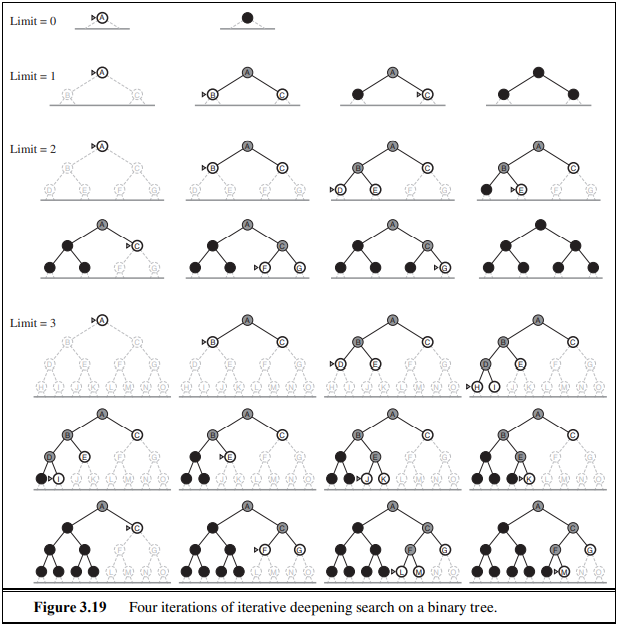
- Bidirectional search
- 탐색을 Start와 Goal에서 각각 시작하는 양방향 탐색. 각각은 BFS로 탐색한다.
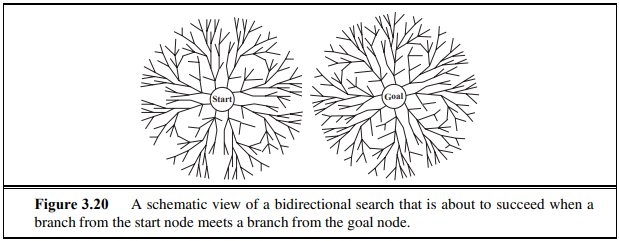
3.4.7 Uniformed search strategies들 비교

구지 위에 있는거 왜우지 말고 그냥 Yes, NO 인지만 외우기
3.5 Informed(Heuristic) Search Strategies
3.5.1 Greedy best-first search
평가 함수 F(n), 현재 노드에서 목표 노드까지 빨리 다가가게끔 하는 함수인 straight-line distance heuristic을 사용한 H(n)이라고 할때
F(n)=H(n)
3.5.2 A* search
f(n)=h(n)+g(n) 출발지부터 n까지 드는 실제 cost(g(n))와 n부터 목적지까지 드는 비용의 최솟값 h(n)을 더한 f(n)의 최솟값을 구하여 A* 알고리즘의 최적의 해를 구할 수 있다.
Optimality of A*(시험)
A* 를 설명하고 또한 그 Optimality를 증명하는데 consistency의 정의를 이용하시요.
A* 의 Optimality를 보이기 위해선 tree-version search에서는 admissibility(goal에 이르는 cost를 overestimate 하지 않는다)를 보이면 되고 graph search에서는 consistency함을 보이면 된다. consistency를 증명하기에 앞서 노드 n에서 action a를 취해 successor인 n'노드로 이동하는 비용을 c(n,a,n')이라 할때 h(n)<=c(n,a,n')+h(n')인 관계가 있고, 이를 triangle inequality라고 한다. 이를 이용하면 다음과 같은 관계식을 얻을 수 있다.(g(n')=c(n,a,n')+g(n))임도 이용한다.
f(n')=h(n')+g(n')=h(n')+c(n,a,n')+g(n)>=g(n)+h(n)=f(n)
f(n)=h(n)+g(n)에서 h(n) 이 admissible heuristic이라면 h(n)의 값은 실제 비용을 절대 넘지 않는다. (h(n)은 n부터 목적지까지 드는 비용의 최솟값)
g(n)은 출발지부터 n까지의 실제 비용이므로 h(n)과 g(n)의 합인 f(n)은 절대 실제 비용을 초과하지 않는다. 따라서 A* search는 optimality가 있다.
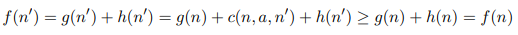
앞에 노드보다 현재노드의 값이 점차커진다는 것을 의미함
3.5.3 Memory-bounded heuristic search
iterative-deepening A 알고리즘 (IDA 알고리즘)은 A* 알고리즘의 사용 메모리를 줄이기 위한 방법으로 탐색 깊이보다 f-cost(g+h)의 최선의 값을 이용한다.
3.6 Heuristic Functions

h1과 h2의 다른 값을 사용하였을 때 h1이 더 심플하지만 h1이 더 많은 Search cost를 발생하게 된다.
4단원
4.1.1 Hill-climbing search와 문제점
Hill-Climbing Search : 항상 현재 상태보다 나은 선택만을 한다. local greedy best-first search 이며 상태를 저장하지 않는다. 주변의 node들이 자신보다 낮은 상태인경우 maxima로 인식하여 search를 종료한다.
문제점
- 결점 1: local maxima : global maxima는 따로 있음에도 이웃하는 값이 자신보다 크지 않아서 local maxima에서 검색이 끝날 수도 있다.
- 결점 2: Ridges(능선) : local maxima가 여러개 존재함으로써 greedy search가 어려워짐
- 결점 3: Plateaux(고원) : 평탄한 부분이 나타나는 것으로써 local maxima일수도 있는데, 이때 search시 plateau 바깥으로 빠져나가지 못할 수 있다.
4.1.2 Simulated annealing
some down hill moves를 허용하는 stochastic bill climbing search의 일종이다. annealing schedule에 맞춰서 down hill move를 하는데, 시간이 흐를 수록 그 빈도가 줄어든다. schedule은 temperature value를 시간 t에 대한 함수로 나타낸 것이다.
4.1.3 local beam search
search할 때 1개의 node가 아닌 k개를 동시에 가지고 search하는데, 처음 k개에서 목표 값이 나오지 않을 경우 다음으로 최적인 k개의 노드를 찾아서 검색하고 이 때 목표 값이 나오면 중단하고 안 나오면 계속 search한다.
4.1.4 Genetic algorithm
처음에 limited population으로써, k개의 node를 임의로 설정한 후 그로부터 cross(썪는다)와 mutation(돌연변이화)등 initial population을 결합시켜 다음 검색노드를 찾는다. (좋은 것들끼리 몇 번이고 크로스 오버 시키고, 변화시킨다.


알고리즘 암기
4.3 Searching with Nondeterministic Actions(내용 이해)
4.3.1 The erratic vacuum world
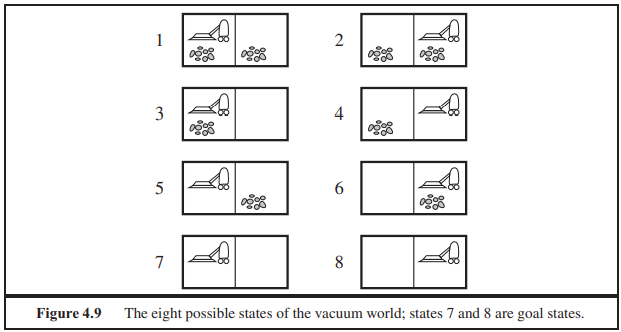
The erratic vacuum world에서는 다음의 행동들을 취하게 된다.
- 더러운 공간에 적용될때 더러운 공간을 치우고 근처의 더러운 공간도 함께 청소한다.
- 가끔식 카펫에 더러운 먼지를 더 뿌린다.
4.3.2 AND-OR search trees
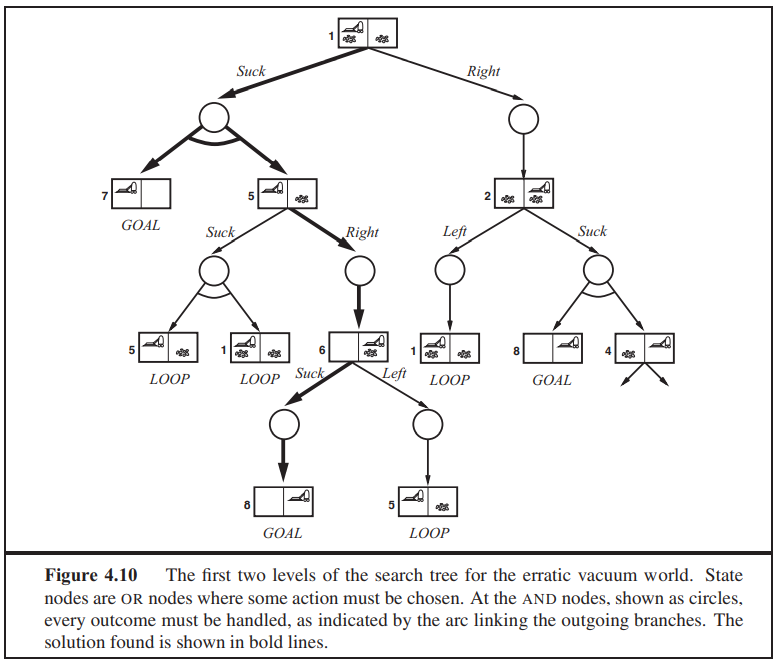
위와 같이 문제에서 어떤 경우들이 생길 것이다. 만약에 어떤 경우라는 조건으로 인하여 OR로 나뉠 수 있다면 ○으로 표현한다.
4.3.3 Try,try again
뭔가 아래쪽같은 문제가 나온다는 데 확인해 보기
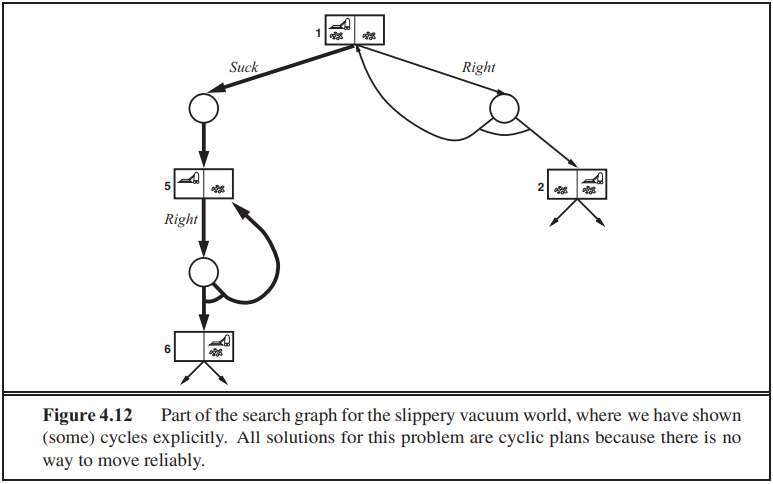
7. Logical Agents
7.4.4 A simple inference procedure

정리하면 ∧는 AND ∨는 OR ¬는 not을 ⇔는 XNOR 즉 둘이 같은 bool이면 True를 의미한다. 단 ⇒는 함의라고하여서 전제가 거짓인 명제 논리 문장은 결론과는 무관하게 무조건 참이다. 이를 이해하기 위해 "만일 P가 참이면 나는 Q가 참이라고 주장한다. 참이 아니면 나는 어떠한 주장도 하지 않는다." 라는 문장으로 생각해 보자. 즉 어떤 주장도 하지 않았기에 무슨 말을 지껄이든 전제가 거짓이기 때문에 결론을 신경쓸 필요없이 해당 복합문장은 참이라는 의미이다. 그래서 전제가 참일때 결론을 신경써서 결론이 거짓이 되면 복합문장은 거짓이라고 판정하는 것이다.
| TransForm |
|---|
| ab = ba |
| a+b = b+a |
| ((ab)c) = (a(bc)) |
| ((a+b)+c) = (a+(b+c)) |
| ~(~a) = a |
| a⇒b = ~b⇒~a(함의) |
| a⇒b = ~a+b (전제가 거짓이거나 결론이 참이거나) |
| a⇔b = ((a⇒b)(b⇒a)) (동치, 상호조건) |
| ~(ab) = ~a+~b |
| ~(a+b) = (~a)(~b) |
| a(b+c) = ab + ac |
| a+(bc) = (a+b)(a+c) |
7.5 Propositional Theorem Proving
암기는 다음 세가지
- deduction theorem(연역이론)
For any sentence α and β, α|=β if and only if the sentence (α=>β) is valid
즉, implication(결론)이 valid 하면, legitimate한 inference rule임을 알 수 있다.
[첫번째 줄만 적어주어도 된다.] - resolution rule(분해 규칙)
resolution rule은 두 개가 존재한다.
(p∨q)∧(¬q∨r) = p∨r 와 같은 과정을 complementary literal을 제거하는 것이다.
(p∨q)∧(¬q∨p) = p∨p 와 같은 과정은 p∨p를 하나의 literal p로 만들어 줄 수 있는데 이를 factoring을 이용하여 할 수 있다. - ground resolution theorem
만약 a set of clause가 unsatisfiable하다면, 이들 clause의 resolution closure은 empty clause를 포함한다.


deduction theorem 은 정리하면 다음과 같다.
For any sentence α and β, α|=β if and only if the sentence (α=>β) is valid
즉, implication(결론)이 valid 하면, legitimate한 inference rule임을 알 수 있다.
[첫번째 줄만 적어주어도 된다.]
이를 이해하기 위해 다음 용어들을 설명한다.
a≡b : 서로 동치이다.
a|=b : a가 b 문장을 함축한다.(한 문장이 다른 문장을 논리적으로 따른다)
7.5.1 Inference and proofs

문제에서 위와 같이 생긴부분을 증명하라는 문제가 나옴 (a⇒b, a)/b
a⇒b는 (¬a∨b) ,a 는 ∧a 그리고 /b는 ⇒b 이다.
정리하면 (¬a∨b)∧a⇒b 이고 이걸 다시 전개하면
¬((¬a∨b)∧a)∨b 라는 결론에 도달하게 된다.
7.5.2 Proof by resolution
Conjunctive normal form(CNF) = product of sum
명제를 표현하는데 있어서 괄호 안에 or로 연결되어 있고 괄호와 괄호 사이는 and로 연결되어 있는 것으로 논리곱 표준형이라고 부른다. CNF형태는 보기에는 복잡해 보이지만 resolution을 적용할 수 있기에 사용한다.

A resolution algorithm
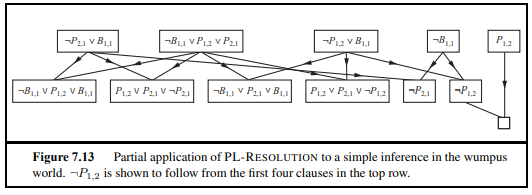
empty clause : 식의 전개 결과물이 아무것도 없는 것을 이야기 함
ground resolution theorem
만약 a set of clause가 unsatisfiable하다면, 이들 clause의 resolution closure은 empty clause를 포함한다.
7.5.4 Forward and Backward chaining
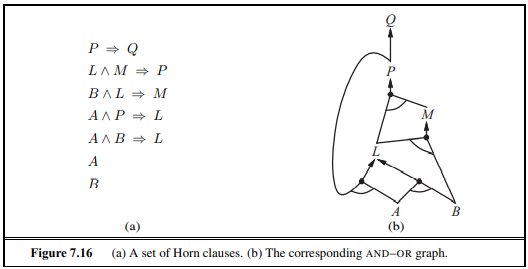
위와 같이 그리는거 공부해 두기 별거 아님 그냥 ∧은 두 상황을 묶어서 ⇒로 뭔가를 가리키면됨
8. First-Order Logic
https://doorbw.tistory.com/34?category=684964
https://blog.naver.com/ndb796/220568481092
