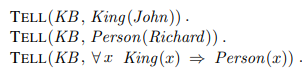
8.3 Using First-Order Logic
이번장에서는 앞에서 배운 logical language를 사용하는 방법에 대해 배워보도록 하자
8.3.1 Assertions and queries in first-order logic
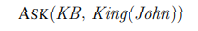
위와 같이 John이 King인지를 물어보아서 True 혹은 False를 반환할 수도 있다.
8.3.2 The Kinship domain
이번에는 또다른 예제인 kinship(친족) 혹은 가족관계에 대해서 다루어보자
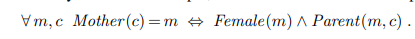
예를 들어서 c의 엄마가 m이라고하면 여성인 m은 c와 부모의 관계로 묶여 있다는 예시를 들 수 있다.
하지만 모든 문장들이 공리(axiom)인 것이 아닌 정리(theorem)일 수 있다. 즉 자명한 결론으로 부터 도출된 값일 뿐일 수 있다는 것이다.
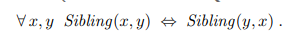
예를 들어 위와 같이 x와 y가 형재 관계라면 y와 x의 형제 관계이기도 한데 추후에 이와 같은 것으로 추론(inference)의 과정을 거치게 될 것이기 때문에 이런것을 미리 정리(theorem)을 만들어 놓는 것이다.
8.3.3 Numbers, sets, and lists
수자들은 자명한 진리로 부터 어떻게 커다란 이론이 나올 수 있는지를 보여주는 예시중에 하나이다. 우리는 자연수 혹은 양수만을 이번에 설명하게 될 것인데 Peano axioms(페아노 공리) 은 자연수랑 양수에 대해 정의를 내린다. 이때 자연수는 재귀적으로 정의되어 진다.
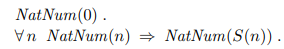
즉, 0은 자연수이고, 모든 n에 대해 n이 자연수라면 S(n)은 자연수라는 것이다. 그리고 0, S(0), S(S(0))식으로 쭉 이어져 나가게 된다.
8.4 Knowledge Engineering in First-Order Logic
여기에서는 본문에서 나오는 어떤 상황을 놓고 First-Order Logic으로 Representation하라는 문제가 나오게 된다.
8.4.1 The knowledge-engineering process(시험 x)
지식 공학 과정을 이야기 하면 이 과정에는 knowledge base에는 사용자가 아닌 어떤 전문가 혹은 특정 영역에 발생하는 실재 지식을 가지고 KB에 집어넣는 것을 지식 공학 과정이라고 생각해야 한다.
앞에서 TELL 안에 정보를 집어넣었던 것과 같이 당연하지만 KB 안에 지식을 집어넣는 것을 지식 획득(knowledge acquisition) 이라고 부른다.
그런데 만약에 의사가 KB에 직접 지식을 넣는 경우도 존재하지만 실재로는 전문가가 직접 AI 시스템에 어떻게 정보를 전달해야 하는지 모르기 때문에 AI와 전문가 사이의 인터뷰를 하는 컨설턴트 즉 Knowledge Engineer가 존재한다.
하지만 Knowledge Engineer가 전문가의 지식을 알 수 없기 때문에 많은 경우에 지식 획득에서 문재가 생긴다고 하며 이 과정에서 정보를 자동 추출하는 과정을 Machine Learning을 사용하고 있으나 아직까지 인간의 전문지식을 표현하는 방법을 잘 모른다고 평가되고 있다.
8.4.2 The electronic circuits domain
이번장에서는 디지털 회로에 대해 추론할 수 있는 존재론(ontology) 및 지식 기반을 개발할 것이다.
Identify the task
디지털 회로와 연관된 많은 추론 업이 존재한다. 가장 높은 단계에서는 회로의 기능을 분석하는 게 존재한다. 그리고 그 아래로는 더 세부적인 분석 단계들이 존재하게 되는데 시간 지연, 회로 영역, 전력 소비, 제작 비용 등등 각 레벨은 추가적인 지식을 요구하게 된다.
Assemble the relevant knowledge
electronic circuits을 위한 디자인을 의미한다.
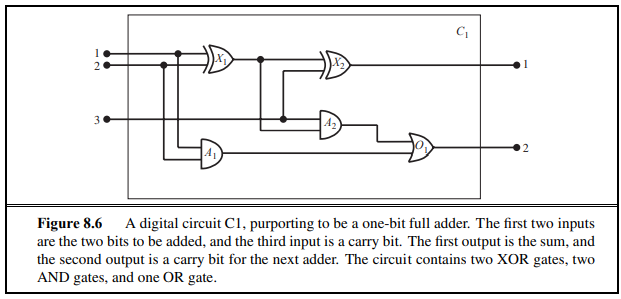
위와 같이 AND, OR, XOR 를 사용하여서 각 위치에 배치함으로써 우리가 미리 생각한 회로를 설계해 볼 수 있다.
이 후 수업은 시험에 나올 단원들에 대한 설명으로 마치었습니다.
