9.5.4 Completeness of resolution(시험)

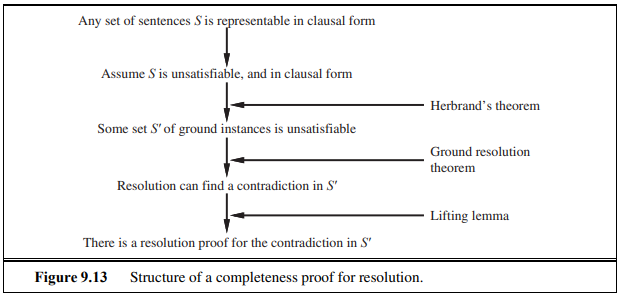
Herbrand universe를 만들기 위해 Herbrand base를 만들어서 우리가 원하는 결론을 부정해서

시험에서는 Herbrand Base를 이해하고 있는지에 대해서만 출제할 예정

• Herbrand universe
  S가 clause의 모음 Hs이라고 할때, Herbrand universe of S는 다음의 룰을 따르게 된다.
  
  A와 B라는 Constant가 정의되어 있을 때 함수에 따라서 점차적으로 무한으로 늘어난다. 하지만 이렇게 늘어나는 것 자체가 무리한 일일 수 있다. 그렇기에 Generate한 모델을 만들어 낸다는 것이 쉬운일이 아니다. 하지만 이렇게 한 것이 모든 Herbrand를 다루는 것이 아님에도 사용하는 이유는 우리가 이렇게 하였을 때 이것만으로도 어떠한 형태를 찾아낼 수 있기 때문이다. 이때 함수값도 하나의 Constant로 나타나기 때문에 Constant를 가지고 a Set of Clause 다른 Clause와의 결합을 통하여 Empty Clause가 나타나는지를 보는 것이다.

• Saturation
  그래서 함수에서 나온 것들을 다시 함수에 적용하는 것

• Herbrand base
  

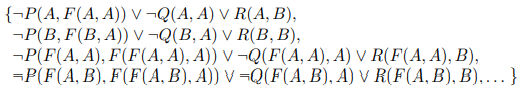
herbrand's theorem : 작은 부분을 가지고도 empty theorem이 나온다.

그래서 S'을 ground sentences의 서브set이라고 할때. resolution closure RC(S')은 empty clause를 포함하고 한다. 또한 내부에는 모순을 함유하고 있다.

lifting lemma

Forward Chaining을 하는데 deductive databases 역시 사용이 된다.
logic programming systems

p361

10 Clasical Planning

다루기는 하지만 문제로 나올지는 확실하지 않음

PLANING이라는 것이 Search와 같이 작동을 한다.

인공지능에서는 Start에서 Goal로 가기위해서는 하나를 뽑고 하나를 움직이는 과정이 필요하다.

만약 하드디스크가 존재한다고 하더라도 하드 내에 데이터를 찾을 때 Job Planning을 세워 작업별로 우선순위를 두게 된다.

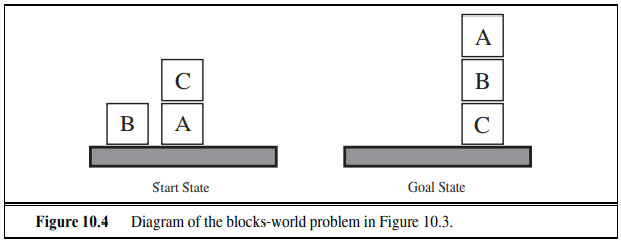
10.1.2 Example : The spare tire problem

대표적인 예로 spare tire문제가 존재한다. 이 문제와 같은 경우 Planing 문제를 Search 문제로 바꾸어 버린 사례이다.

이와 같은 경우에도 모든 가능한 경우를 추출해서 문제를 해결할 수 있는 최적의 경우를 찾아낸다.

Planing 문제는 Search와 유사하다보니 Search 문제의 응용문제라고 부르기도 한다.

10.4.2 Planning as first-order logical deduction: Situation calculus

7장에서의 움프스 월드의 예제를 가지고 사람과 움프스가 움직이는 경우를 가지고 다룬다. 여기에서는 움프스가 움직이지 않는다면 내가 다음은 알 수 있어도 다다음은 어떻게 움직이는 지 확인할 수가 없다.

만약 움프스가 반드시 올 수 밖에 없는 경우라면 나는 그냥 Die 하면 된다. 여기에서 좀 더 넓게 생각해보면 나는 모르고 간것이지만 움프스가 딴 곳으로 가는 것이라 서로 비켜나갈 수 있다.

그렇기에 고려해야하는 것은 움프가 어디에 어느 시간에 있는지를 정확하게 알 고 있는 것이다. 즉 여기에서는 time variable을 따로 가지고 있어야 한다는 것이다.

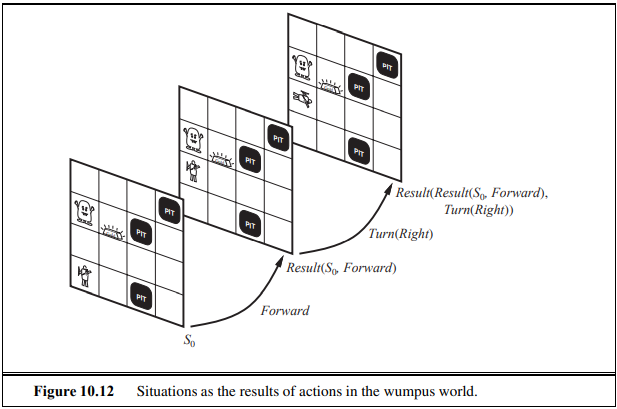
이 Situation Calculus를 사용하여서 중간에 사고가 났다면 원래의 schedule로만 하는 것이 아닌 time에 따라서 다른 방법을 고려한다.

• 그래서 처음 상태를 situation이라고 부른다. 만약 s가 situation이고 a가 action이라고 할때 RESULT(s,a)또한 situation이다.
• 한 상태에서 다음 상태로 변화할 수 있는 것을 fluent라고 부른다.