=== Chapter 5: Data Link Layer (1) ===

We are here

• OSI 7 layer model

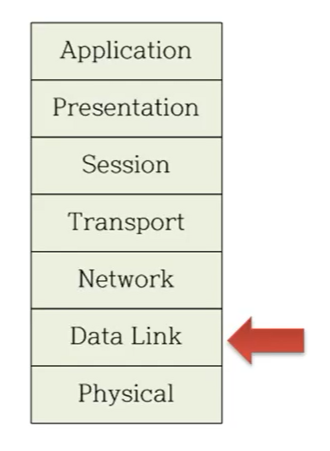
Data Link Layer

• Role of link layer
– Transfer frames between directly connected devices

직접 연결이 된 송수신자의 frame을 전달해주는 역활

• Link layer services
– framing
– error detection / correction
– multiple access control

프레임 나누기
error detect / 올바르게 맞추기 (ARQ -> 에러 확인시 재전송)
회선이 공유될때 충돌이 발생하지 않도록 하는것

=== Framing ===

1. Framing

• Bits are transmitted continuously -> bit stream

• 010110110001100100100100100111101001011

• The receiver should understand the received data

• The first thing is to do is to divide the bit stream into meaningful block of data -> “frame”

데이터를 전기신호로 바꾸어서 전달하게 되는데 수신하는 디바이스가 어디에서부터 어디까지가 하나의 프레임인지를 알아야 한다. 그래야 어디에서부터 어디까지가 헤더이고 데이터인지를 알 수 있다. 그래서 Framing은 어디에서부터 어디까지가 헤더와 데이터인지 알려주는 것이다.

link layer의 기본단위는 frame이다.

Reading by Punctuating

“Elizabeth, New Jersey, when my mother was being raised there in a flat over her father’s grocery store, was an industrial port a quarter the size of Newark, dominated by the Irish working class and their politicians and the tightly knit parish life that revolved around the town’s many churches, and though I never heard her complain of having been pointedly ill-treated in Elizabeth as a girl, it was not until she married and moved to Newark’s new Jewish neighborhood that she discovered the confidence that led her to become first a PTA “grade mother,” then a PTA vice president in charge of establishing a Kindergarten Mothers’ Club, and finally the PTA president, who, after attending a conference in Trenton on infantile paralysis, proposed an annual March of Dimes dance on January 30 – President Roosevelt’s birthday – that was accepted by most schools.”

• Philip Roth, “A plot against America”

이게 한 문장인데 이걸 보내면 이해하겠는가?

Framing

• Fixed-size framing

• Variable-size framing

1) Fixed-size Framing

• Fixed number of bits
• No delimiter necessary
• May cause inefficiency
– Suppose the frame size is 1000 bits
– If I have only 50 bits to send, the frame still has to be 1000 bits

비트 사이즈가 정해져 있는 방식이다. 그래서 delimiter가 필요 없다. 문제점은 1000bit로 정해놓으면 50bit밖에 보낼게 없어도 50 bit 뒤에 필요없는 비트를 붙여서 overhead가 있다.

2) Variable-size framing

• Each frame can have different number of bits
• Delimiter necessary to identify frames
• Can build frames according to the data sent -> efficient
– If I have 50 bits to send -> I can make the frame 50 bits

수신자가 받아야 하는 frame의 사이즈를 모르기 때문에 delimiter을 사용하게 된다. delimiter은 어디가 시작이고 끝인지 알려주는 것이다.

---

• Flag: marker that points the beginning and the end of a frame
• Header: bits inserted before the data for control purposes
• Trailer: bits inserted after the data for control purposes
• Data/Payload: data to be sent

Flag(maker)을 사용해서 프레임의 시작과 끝을 나누어준다.
그리고 그 내부에는 Header, Trailer, Data/Payload가 붙게 된다.

Frame Structure

• Defines size and meanings of fields in a frame

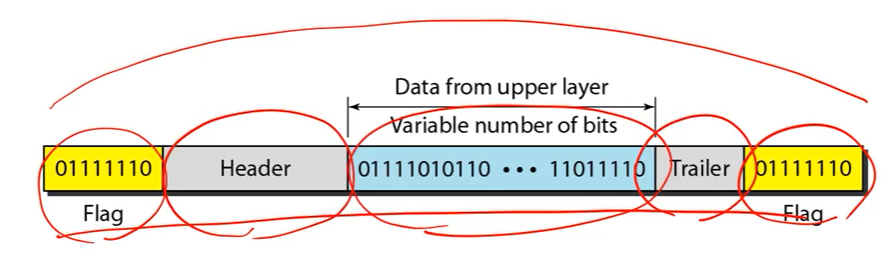
그래서 프레임의 시작과 끝을 정의하면 각 성분이 어디에서 어디까지인지 정해져 있어야 수신자가 끊어읽을 수 있다. 그래서 이것을 Frame Structure이라고 부른다.

• Start/end marker
– e.g. 01111110

• What if “01111110” appears in the payload?
– Suppose payload is “0010101111110100”
– Assume there is no header/trailer
– Then the frame is “01111110001010111111010001111110”
– What is the problem?

시작과 끝을 01111110으로 해놓자. 이렇게 해놓으면 수신자가 이것을 받으면 이게 시작이고 끝이구나라고 알게된다.
한가지 문제점은 비트패턴이 데이터안에 나올 수 있다는 것이다.

Bit Stuffing

• Problem
– If the marker pattern appears in the payload, the receiver
will think it as an end marker – leads to wrong framing
• Solution – Ensure the marker pattern does not appear in the payload – If “11111” is found, add a “0” after the pattern
• Bit stuffing – The receiver removes “0” after “11111”, since it is the stuffed bit

일부러 Bit pattern을 marker에 나오는 패턴과 일치하지 않도록 만드는 것이다. 예를 들어서 flag가 01111110으로 설정되었는데 data에 11111이 나오는 경우 이 뒤에다 0을 붙여주는 것이다.
그럼 수신자는 1이 5개가 나오면 뒤에 있는 0은 임의로 붙인거라고 생각하고 제거해주면 된다. 그래서 송/수신자의 코드가 맞아야 한다.

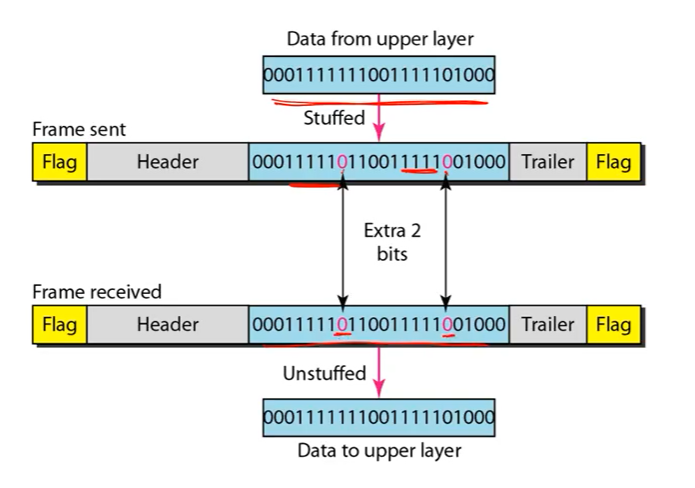
결국 위와 같이 flag와 동일한 비트는 생기지 않게 된다.

Byte Stuffing

• The same purpose as bit stuffing
• Insert a byte after a marker byte pattern
• Used in systems that process data in unit of bytesIntroduction to Computer Networks

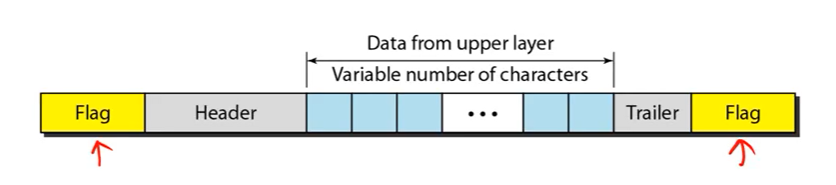
Byte단위로 데이터를 처리하는 system이 존재할 수 있다. 이 경우에는 byte 단위로 stuffing을 해준다.

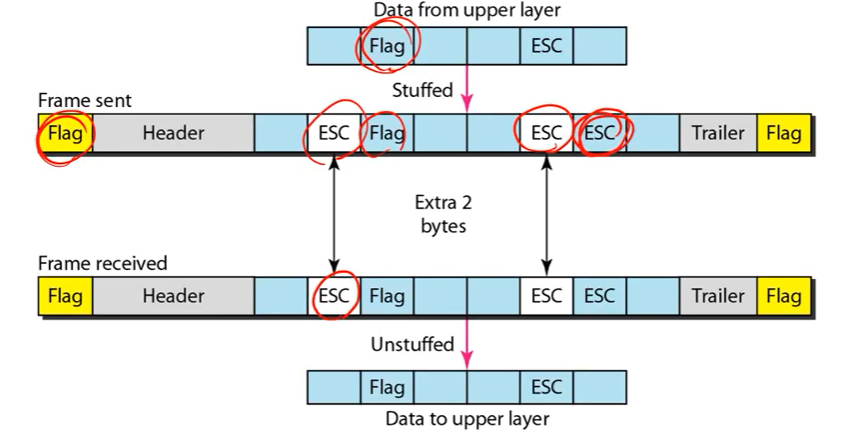
특정 Byte를 Marker로 사용하겠다는 의미이다. 그래서 Flag와 유사한거는 ESC 바이트를 붙이고 ESC와 유사한게 나오면 또 ESC를 붙여준다.

• TinyOS is an operating systems used for small embedded systems such as sensors

• TinyOS uses 7E as start/end marker

• If 7E appears in the payload, it is changed to 7D 5E
• If 7D appears in the payload, it is changed to 7D 5D
• 7E -> 7D 5E
• 7D -> 7D 5D

이 시스템에서는7E를 start/end marker로 사용한다. 데이터 안에서 이와 유사한 바이트가 나오면 7D 5E로 바꾸고 7D가 나오면 7D 5D로 바꾸어준다.

=== Errors ===

1. Errors

• Definition of “error” in data link layer

• Sender sent bit 0
– Receiver thinks sender sent bit 1, or
– Receiver cannot figure out which bit was sent

• Sender sent bit 1
– Receiver thinks sender sent bit 0, or
– Receiver cannot figure out which bit was sent

에러에 관해서 처리해주는 것은 link, Transport(TCP)에서 해준다.

에러라는 것은 곧 0으로 보냈는데 1로 도착을 하는 경우들을 에러라고 이야기 한다. 일단 보냈는데 수신자가 이게 도대체 어떤 bit를 보냈는지 유추못하는 경우

Why do errors occur?

• attenuation, distortion, noise

• amplitude, frequency and phase of signal changes

진폭, 주파수, 위상등이 신호의 특징이다. 디지털 데이터를 보내는 방법은 신호의 특징을 가지고 디지털 데이터를 구분할 수 있도록 하는 것이다.

신호의 감쇄, 신호의 특징이 변경, 노이즈(다른 신호)

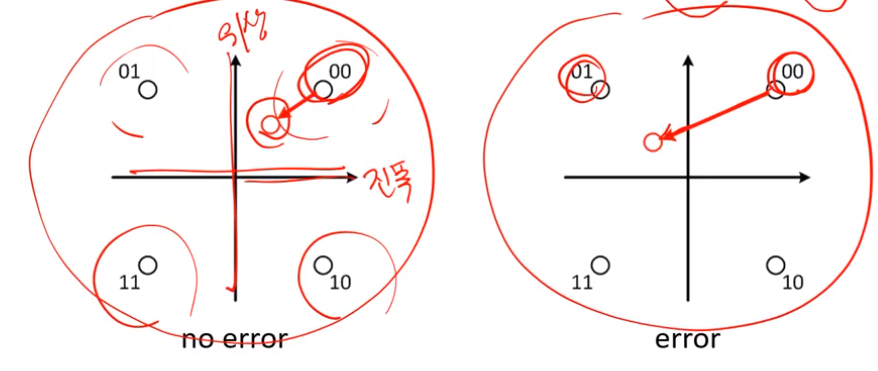
그래서 이러한 신호를 4가지로 나눈것이다. 나누는 기준은 개발자가 결정하게 된다. 만약에 신호를 보냈는데 다른 영역으로 가면 잘못된거라고 이야기 한다.

n-bit error

• Suppose sender sends a block of data “01101100”.
• Suppose the receiver receives “0110110 1 ”.
• Then we say a 1-bit error occurred.

위와같은 경우를 1-bit error이라고 한다.

• If the receiver receives “01011101” -> 3-bit error

위와같은 경우를 3-bit error이라고 한다.

• The size of data block depends on the unit of error detection/correction

이런것들이 중요한 이유는 에러가 많이나면 날수록 비트를 짧게 잘라서 보내야 한다. 그래서 에러가 많이나면 날수록 한번에 보낼 수 있는 데이터의 사이즈를 정하게 된다.

Error detection vs. correction

• Error detection
– Know that an error has occurred
– Don’t know how to correct

에러가 있는데 어떻게 수정해야 하는지 모르는 경우를 이야기 한다.

• Error correction
– Know that an error has occurred
– Can correct the error

에러가 난것도 판단하지만 송신자가 무엇을 보내려고 했는지도 알아내는 것을 이야기 한다.

• How can we know that an error has occurred?
– Need to insert additional bits to the original data

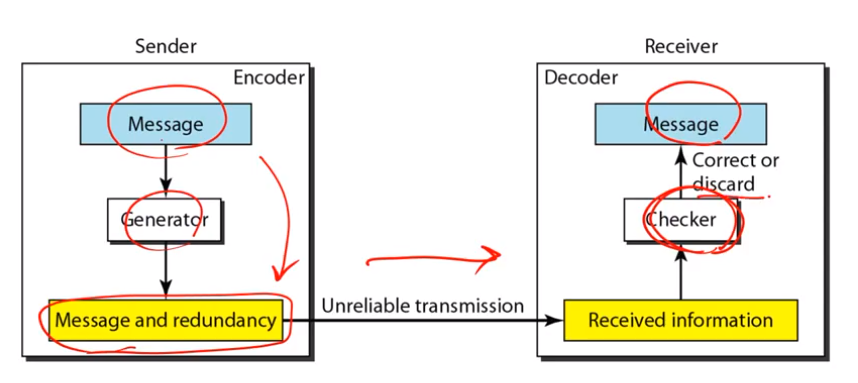
에러를 어떻게 확인하는가? 보내고자 하는 메세지에 Generator에서 Message and redundancy를 생성한다. Error detection을 위해서는 메세지가 커지게 된다. 그리고 이것을 수신자로 보내게 된다. 수신자는 이 바뀐 형태의 데이터를 원래의 데이터로 바꾸어야 한다. 이때 redundancy를 이용해서 에러를 확인한다.
하지만 수정을 할 수 있으면 복원하거나 못하면 버린다.

=== Block Coding for Error Detection/Correction ===

1. Block coding

• Block coding was used in physical layer to avoid continuous zeros
• Block coding is also used for error detection/correction

한 block의 bit들을 바꾸어서 전송한다.

• Terms
– dataword: a block of original message
– codeword: block-coded message

dataword : 원래의 메세지에서 일부만 땐 형태
codeword : original word를 codeword로 바꾸어서 전송한다.

크기차이 data word < codeword

• Generate an n-bit codeword from a k-bit dataword
– dataword: k bits
– codeword: n bits
– r: redundancy
– r = n – k

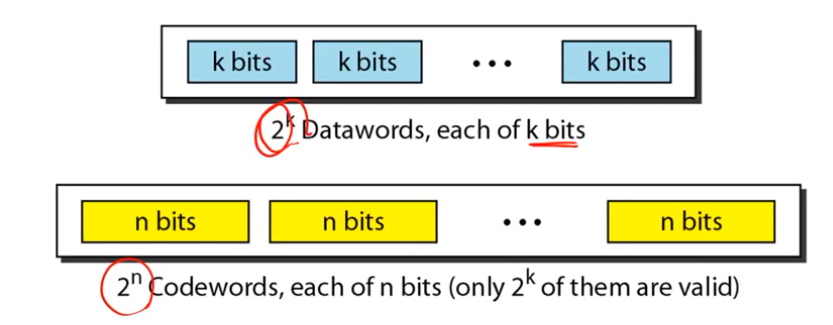
dataword는 k bit인데 이것으로 표현할 수 있는 데이터의 숫자는 2^k이다. 이것을 n bit의 codeword로 바꾸었을때 codeword는 2^n만큼 표현할 수 있다. 그중에서 2^k에 해당하는 bit 패턴들은 원래의 dataword에서 바뀌어서 나올 수 있는게 있고 나머지는 나올 수 없는 것이다. 그래서 수신자 측에서 나타날 수 없는게 있다면 error detection한다.

Error detection using block coding

• We can block-code the message as the table below
• What is k?
• What is n?
• What is r?
• What do we actually transmit if we want to send “01101100”? -> 011101110000

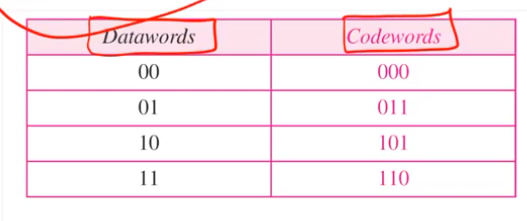
일단 2bit 씩 자르고 그것을 codeword로 바꾸어준다.

수신자는 이것을 받아서 원래의 상태로 바꾸어주면 되는 것이다.

Error detection using block coding
• The sender wants to send “01”.
• The sender will send “011” using block coding.

• Suppose receiver received “011” (no error).
• What should the receiver do?

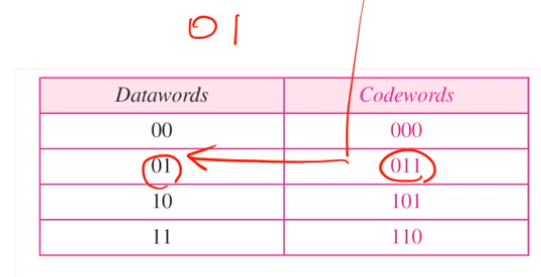
01 -> 011이 보내진다. 011로 받았으면 에러가 없는 거이다.

Error detection using block coding
• The sender wants to send “01”.
• The sender will send “011” using block coding.

• Suppose receiver received “111” (1-bit error).
• What should the receiver do?

01 -> 011 -> 111을 받은 경우 1bit error가 발생한다. receiver은 codeword에서 찾아서 상위로 보낼려고 하는데 111은 없다. 그래서 이건 오류로 본다.

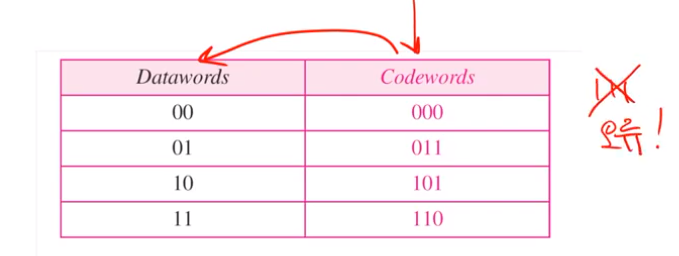
Error detection using block coding
• The sender wants to send “01”.
• The sender will send “011” using block coding.

• Suppose receiver received “000” (2-bit error).
• What should the receiver do?

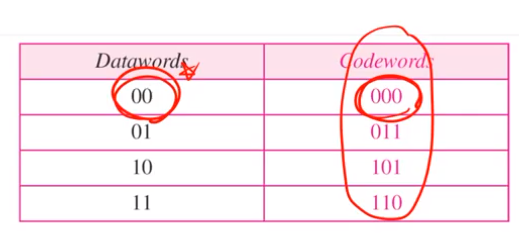
01 -> 011 -> 000 2bit error인데 문제는 codeword에 000이 존재한다. 그래서 상위에 00을 올려준다. 하지만 이건 error detection을 못한것으로 볼 수 있다.

Error detection using block coding
• The sender sends “011”.
– “011” received -> receiver thinks dataword is “01”.
– “111” received -> receiver knows an error has occurred.
– “000” received -> receiver thinks dataword is “00” (wrong)

-> This codeword set can detect 1-bit error, but cannot detect 2-bit error.
-> Can we prove that this scheme always detect 1-bit errors?Introduction to Computer Networks

1 bit는 error detection가능 2bit는 불가능
table을 보면 1bit error은 확실하게 detect 할 수 있다는 것을 어떻게 보장할까?

Error detection using block coding
• Another block coding scheme
• What is k, n, and r?

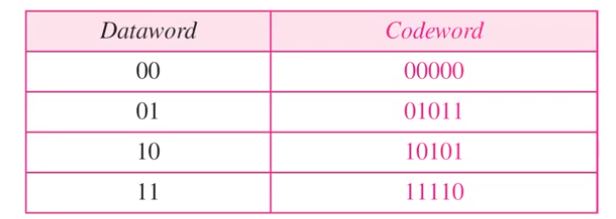
만약 이와 같이 2비트를 5비트로 보내면 어떻게 할까?

Error detection using block coding
• The sender sends codeword “01011”.
• The receiver receives “01001” (1-bit error).

• The receiver knows that there was an error.
• Can the receiver do more than that?

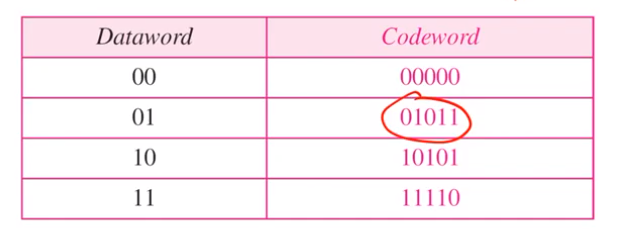
01001 -> 01001 인 경우 수신자가 이것을 확인하고 무언가를 더 할 수 있을까?

Error detection using block coding
• The sender sends codeword “01011”.
• The receiver receives “01001” (1-bit error).

• Among the codewords, 01011 is “the closest” codeword to 01001.
• Thus, the receiver guesses that the dataword was 01.

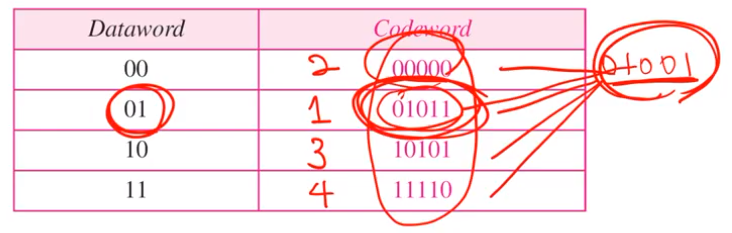
원래로 돌리기 위해 할 수 있는 방법이 무엇일까? 내가 받은 것에서 가장 가까운 것이 무엇인지 생각해보는 방법이 있을 수 있다.

01001을 받으면 00000은 distance = 2 / 01011 dist = 1 / 10101 dist = 3 / 11110 dist = 4

dist = 1인것이 송신자가 보낸거라고 생각하고 error correct할 수도 있다.

Error detection using block coding
• The sender sends codeword “01011”.
• The receiver receives “01001” (1-bit error).

• Let’s assume that there can be only 1-bit errors.
– no 2 or more bits of error
• Then, this codeword set can correct the error.

1bit error만 존재하고 2bit error가 없다고 생각하면 수정은 할 수 있다.

Error detection using block coding
• The sender sends codeword “01011”.
• The receiver receives “00001” (2-bit error).
• In this case, the closest codeword is “00000” (wrong)
– This codeword cannot correct 2-bit error.

• However, the receiver knows that there is an error.
– Because there is no codeword “00001”.
– This codeword set can detect 2-bit errors.
– How about 3-bit errors?Introduction to Computer Networks

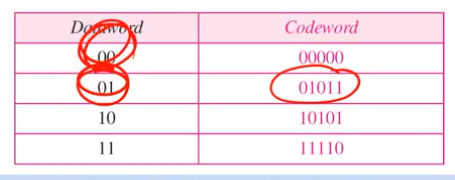
01011 -> 00001
2 bit error가 난 경우 이를 correct할 수가 없다. 하지만 error인것을 판단할 수 있다. 왜냐하면 00001은 없기 때문이다.

3 bit error은 아예 detection도 안되는 것이다.

또한 1bit 에러도 반드시 어디에서 에러가 발생하든지 원래대로 돌릴 수 있어서 correct, detect가능하다는 것이다. 즉 완벽해야 한다.

Error detection using block coding
• What is the logic behind all this?

Hamming distance

• Number of different bits between two codewords
• d(000, 000) = 0
• d(000, 011) = 2
• d(0100, 0010) = 2
• d(10101, 11110) = 3

두 bit stream이 있을때 hamming distance는 몇비트를 바꾸어야 완전히 바뀔 수 있을지를 계산한 것이다.

Minimum Hamming distance

• Given a codeword set, its MHD is the minimum of hamming distance between any two codeword in the set

• What is the MHD of this codeword set?Introduction to Computer Networks

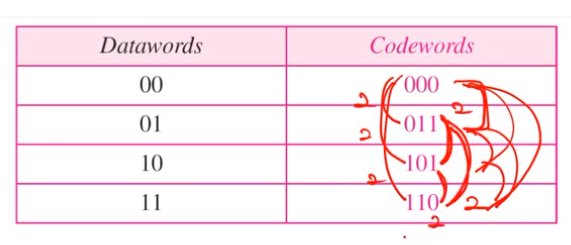
모든 codeword에서 hamming distance를 계산해서 가장 작은 것이 MHD이다.

지금은 아무거나 뽑아서 해도 MHD는 2이다.

Minimum Hamming distance
• What is the MHD of this codeword set?Introduction to Computer Networks

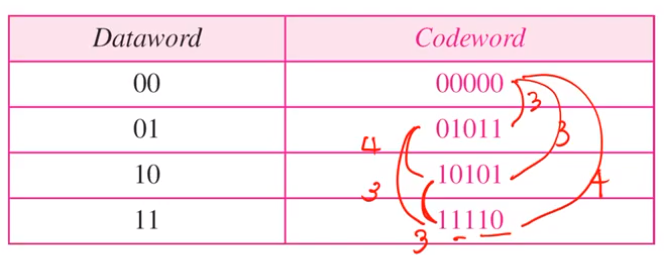
여기는 3이 된다.

• CT : transmitted codeword
• CR : received codeword

• If d(CT, CR) = n, this means there was an n-bit error

• Example
– transmitted: 000
– received: 011
– d(000, 011) = 2, thus 2-bit error

CT는 보낸거 CR은 받은 codeword를 이야기 한다 d(CT, CR) = n이라는 것은 두 codeword가 n비트 차이난다는 것을 이야기 한다.

MHD and error detection

• To detect an s-bit error, MHD of the codeword set must be larger than s.

• dmin > s

error detection을 위해서는 MHD가 s-bit error의 s값보다 커야 한다. 2bit를 detect 하려면 3bit 이상이어야 한다.

• Suppose MHD of a codeword is s+1.
• Pick any codeword, and change s bits or less.
• This should not be in the codeword set, because then the MHD must be less than s+1 .

codeword의 MHD가 s+1이라면 아무 코드나 골라서 s개를 바꾸는 것이다. 그러면 다른 codeword set에 있는 codeword가 될 수가 없다. 만약 그게 안된다면 MHD를 잘 못 계산한 것이다.

• The MHD of this codeword set is 2.

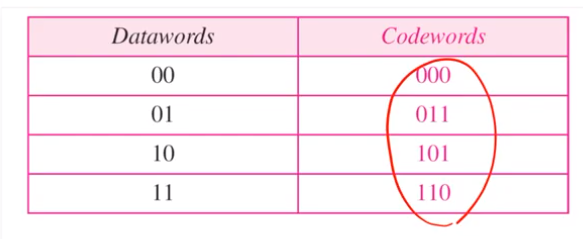
• It means this codeword set can detect up to 1-bit
errors.Introduction to Computer Networks
이와같은 경우는 MHD가 2이기 때문에 1bit까지 검출가능하다.

MHD and error detection
• The MHD of this codeword set is 3.

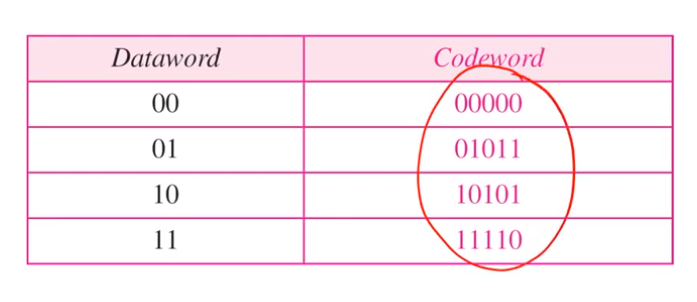
• It means this codeword set can detect up to 2-bit errors.Introduction to Computer Networks

• MHD and error detection
  

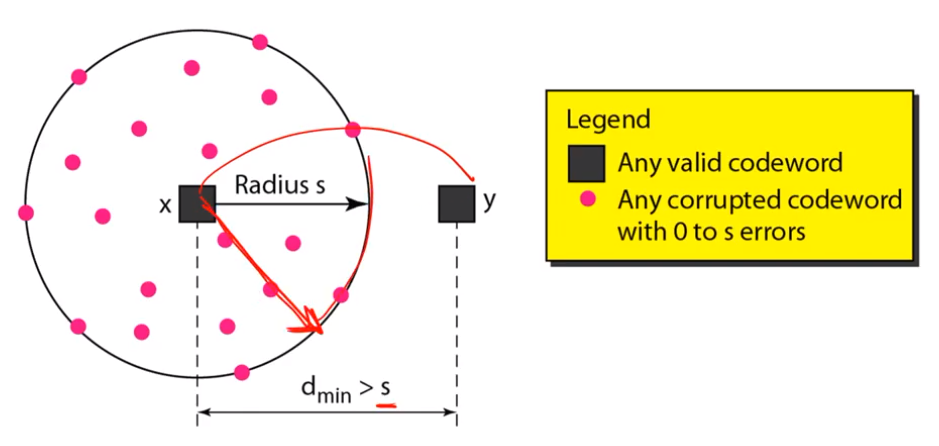
MHD and error correction

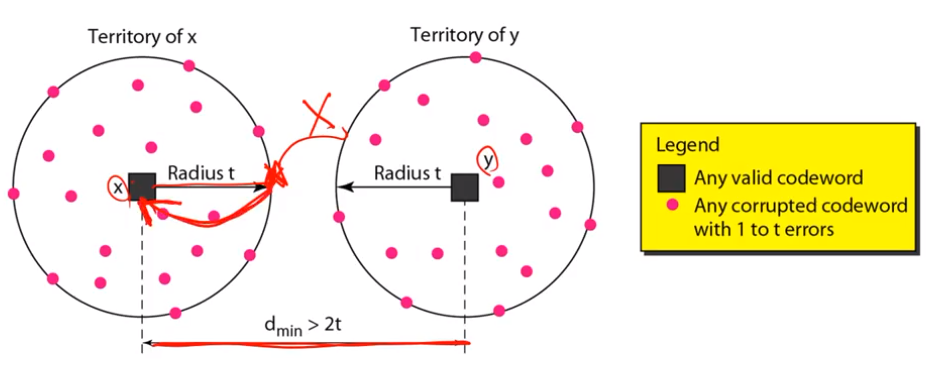
• To correct a t-bit error, MHD of the codeword set must be larger than 2t.

• dmin > 2t

• Suppose MHD of a codeword is 2t+1.
• Pick any codeword (C), and change t bits (C’).
– C’ obviously is not in the codeword set.

• Choose the closest codeword to C’.
• It is C, since other codewords should have hamming distance of at least t+1.

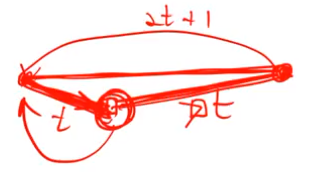
MHD는 2t보다 커야한다. 어떤 코드워드가 MHD가 2t+1이라고 하자 그럼 어떤 코드워드가 있으면 최소 2t+1만큼 떨어져 있어야 한다. 그런데 지금 t-bit error가 발생시 무조건 자신에게 가까운 코드워드로 갈 수 밖에 없다.

• MHD of this codeword set is 3.

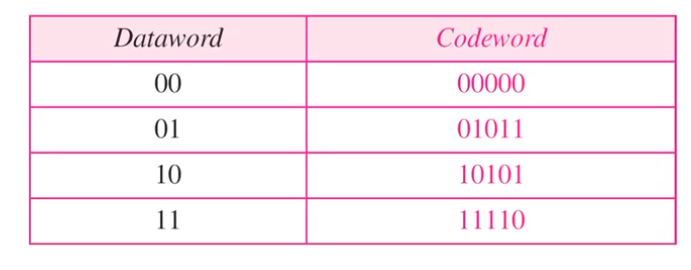
• This codeword set can detect up to 2-bit errors.
• This codeword set can correct up to 1-bit errors.

MHD값을 보고 몇 비트까지 에러 디텍트와 수정이 가능한지 알 수 있다.

Example
• Suppose a codeword set has MHD=4.

• How many bit errors can this codeword set detect? 3

• How many bit errors can this codeword set correct 1