=== Block Coding for Error Detection/CorrectionI(이어서2) ===
4. Checksum
• An error detection method slightly more complex than parity check codes
error detection code이다.
• Suppose we want to send five 4-bit numbers
– 7, 11, 12, 0, 6 = 0111,1011,1100,0000,0110
• Add all numbers and place the sum as the last number
– 7, 11, 12, 0, 6, 36
우선 모든 숫자를 더해서 얻은 값을 마지막에 넣어준다.
• The receiver checks for errors by adding all numbers and comparing with the last number
– 7 + 11 + 12 + 0 + 6 = 36 -> no error!
받는 쪽에서는 5개를 받아서 더해서 그 결과가 원래의 합과 같은지 확인해서 에러인지 체크한다.
• We can also do this like the following.
• Add minus sign to the sum
– 7, 11, 12, 0, 6, -36
• The receiver simply adds all numbers and see if it is zero
– 7 + 11 + 12 + 0 + 6 + (-36) = 0 -> no error!
마지막에 -36을 넣어서 마지막에 합이 0이 되는지 확인하는게 보다 편리하다.
Wrapped Sum
• The problem is: 36 is not a 4-bit number
• We calculate a “wrapped sum”
– 36 is “100100” in binary representation
– keep the lower 4 bits, and add the number to the higher 2 bits
0100
+ 10
--------
0110– The wrapped sum of 36 is 6
다른 비트들이 4bit였다면 checksum도 4bit가 되도록해야 한다. 하지만 36 = 100100이기 때문에 4bit 안에 넣을 수가 없다.
그래서 상위 비트를 잘라서 하위비트에 더해준다. 이것을 wrapped sum of 100100이라고 부른다.
36 -> 6이 된다.
• What is the 4-bit wrapped sum of 45?
• 45 -> 101101 (binary)
1101
+ 10
---------
1111• 4-bit wrapped sum of 45: 15
• What is the 4-bit wrapped sum of 63?
• 63 -> 111111 (binary)
1111
+ 11
---------
10010• This is still over 4 bits!
하지만 이 경우는 여전히 5bit이다. 이 경우에는 다시금 wrapped sum을 한다.
• In this case, wrap one more time
0010
- 1
0011
• 4-bit wrapped sum of 63: 3
Checksum
• Now we need to make the number negative (-6) using 4 bits
• Use 1’s complement to represent -6
• 1’s complement: toggle all bits
– 6 = 0110
– -6 = 1001
• ‘1001’ is 9 in decimal representation
하지만 우리가 넣을 것은 음수이다. 그래서 이때 사용하는 것이 1의 보수이다. 그런데 문제는 이것을 그냥 unsigned로 표현하면 9가 된다. 그러니 checksum값이 9인 것이다. 상당히 복잡하다는 것을 알 수 있다. 어찌되었든 checksum은 1001이다.
• The sender place ‘9’ as the last number
– 7, 11, 12, 0, 6, 9
그래서 일단 이렇게 보낸다.
• The receiver receives the numbers and adds them
– 7 + 11 + 12 + 0 + 6 + 9 = 45
해서 더해보니 값이 45이다.
• Calculate a wrapped sum of 45 (101101)
1101
+ 10
--------
111145 = 101101 이기때문에 wrapped sum을 해준다. 그럼 1111이 나오는데 이를 1의 보수를 취하면 0000이 나오고 이것에 대해 에러가 없다고 평가한다.
• Find 1’s complement of 1111 = 0000 -> correct!
– If the final value is not 0, then there is an error
하지만 어쩌다 보면 에러를 검출하지 못할 수도 있다.
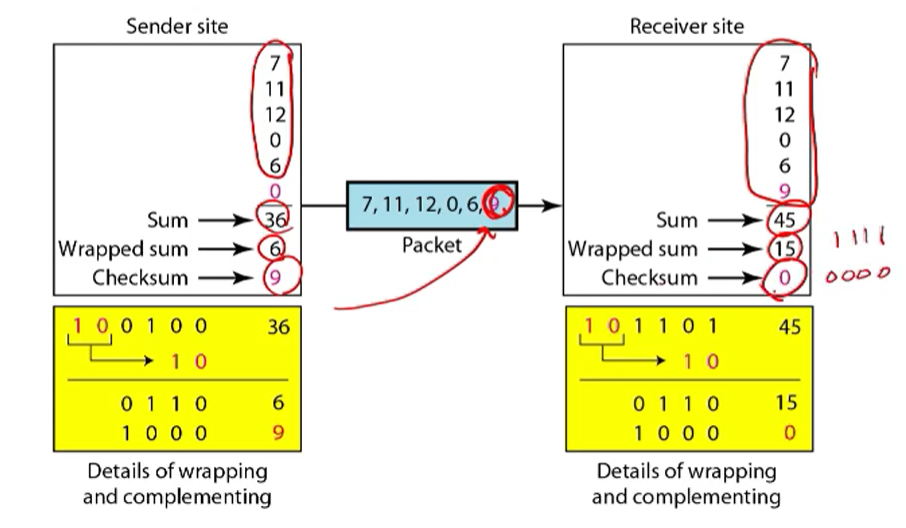
정리하면 위와 같은 그림이 된다.
5. Cyclic Redundancy Check (CRC)
• A complex and powerful error detection method
• Complexity and power of CRC can be controlled by selecting “divisor (generator)”
CRC는 file transfer을 할때 error detection 용도로 많이 사용한다. CRC는 복잡하지만 상당히 powerful하다.
CRC에는 divisor(generator)가 들어간다. divisor를 무엇을 쓰냐에 따라 복잡도와 power가 달라지게 된다.
Modulo Arithmetic
• A basic arithmetic used in CRC and other coding methods
• Modulo-N: use N numbers [0, N-1]
0부터 N-1까지 밖에 없는 것을 이야기 한다.
• Example: modulo-5
– 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4
– 3 + 2 = 0
– 4 + 3 = 2
– 2 – 3 = 4
예를 들어 modulo-5 는 숫자가 [0,4]만 있다고 생각하는 것이다. 그러면 modulo-5의 세계에서 더하거나 빼기를 할 수 있다.
Modulo-2
• Use only 0 and 1
• 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0
• 0 – 0 = 0, 0 – 1 = 1, 1 – 0 = 1, 1 – 1 = 0
• Addition and subtraction lead to the same results
– addition = subtraction
우리가 보고 싶은것은 Modulo-2의 세계이다. 이러한 체계에서는 덧샘과 뺄샘의 결과가 같다.
• Addition and subtraction are equal to XOR
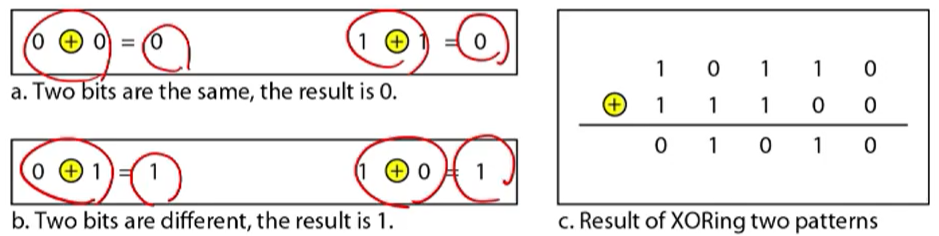
결국에는 XOR의 연산과 modulo-2가 같다.
Cyclic Redundancy Check
• Suppose we use the divisor ‘1011’
• We want to send the dataword ‘1001’
• Since the divisor is 4 bits, we add ‘000’ after the dataword -> ‘1001000’
• Divide ‘1001000’ by the divisor ‘1011’
– Use modulo-2 arithmetic
divisor을 1011을 사용한다고 하자 이때 1001을 전달한다고 하자. 이것을 codeword로 바꾸어서 전송한다고 하자.
첫번째 작업은 divisor가 4bit이다. dataword에 000 3bit를 더해준다.(len(divisor) - 1 만큼 더해준다) => 1001000
두번째 작업은 1001000을 1011으로 나누어 본다. 이때에도 modulo arithmetic 을 사용한다.
• Dividing 1001000 by 1001 using modulo-2 arithmetic
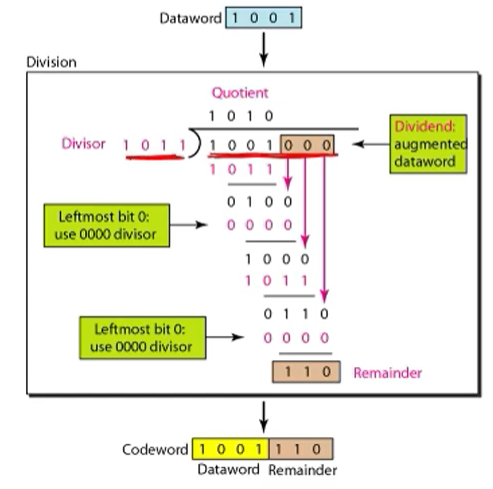
modulo-2 연산을 사용해서 각 자리별로 빼준다. 그러면 나머지가 110이 생기는데 이게 중요하다. 이것을 원래 1001에 붙여주어서 code word를 만든다. 이때 붙여준것이 CRC이다.
• Since the remainder is ‘110’, we add this to the dataword to make the codeword -> 1001110
• Send this codeword
남은 것이 110이기 때문에 dataword 뒷부분에 붙여준다. 그래서 이 코드를 수신자에게 보낸다.
• The receiver receives the codeword and divide the number by the divisor
– If remainder is 0, then there is no error
일단 수신자가 divisor 1011을 알고 있어야 한다. 그래서 받은 값을 divisor로 나누어서 나머지가 000이 나오면 정상적인 코드인것이다.
• If the remainder is not 0, then error detected
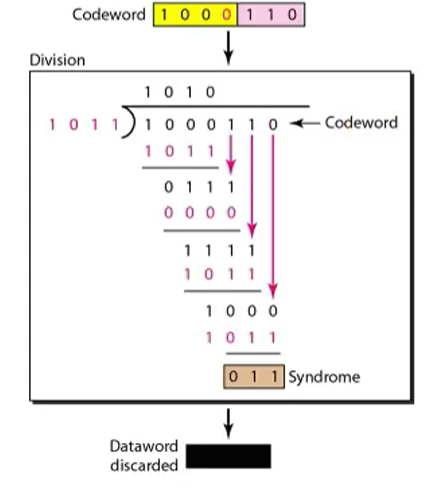
나누어보았는데 000으로 나누어 떨어지지 않으면 에러가 있는것으로 판단된다.
Binary Polynomials
• We can represent a binary number as a binary polynomial
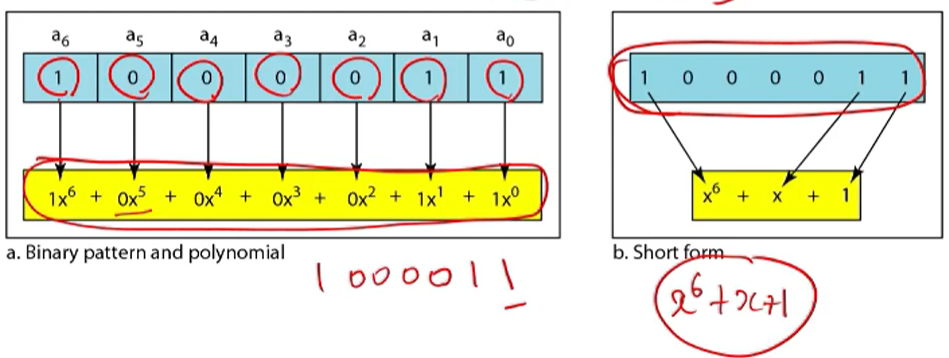
divisor 1011을 그대로 쓰지 않고 다항식 형태로 적는 경우가 있다. binary polynomial은 계수가 0또는 1만 될 수 있는 것을 의미한다.
이진수를 binary polynomial로 표현할 수 있는 것이다. 계수가 0인 항은 표현하지 않아도 된다.
• Division of binary polynomials
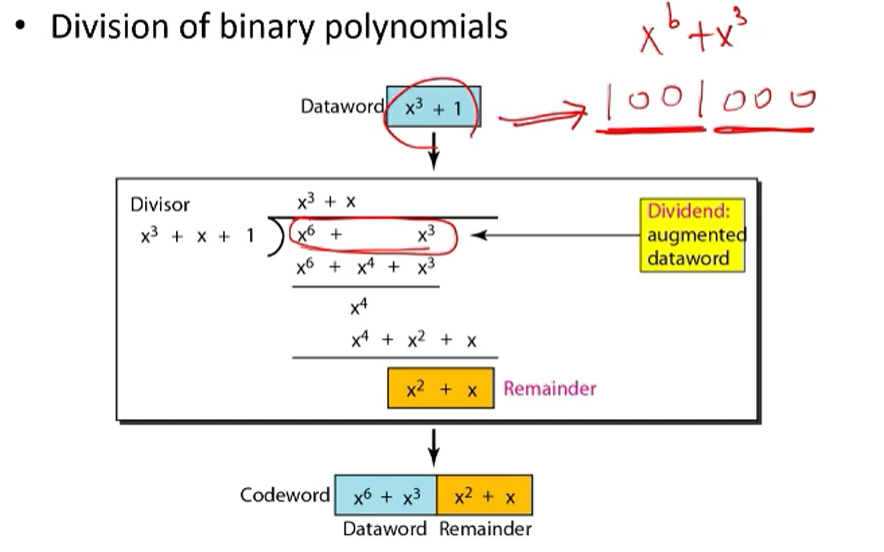
이를 이용해서 다항식의 나눗셈처럼 할 수도 있다. 결국 남은것은 x^2 + x이기에 이것을 remainder에 붙여서 codeword를 만들어준다.
그러면 결국 codeword가 1001110이 된다.
Cyclic Redundancy Check
• dataword(message): M(x)
dataword를 M(x)
• divisor: g(x)
• codeword: T(x)
• T(x) is divisible by g(x)
– Remainder of T(x)/g(x) is 0
우리가 1001을 1011으로 나누엇을때 나머지가 110이 나왔다. 그랬을때 110을 붙이는걸 하는 이유가 무엇일까? 왜냐하면 이렇게 했을때 divisor로 codeword가 나누어 떨어지기 때문이다.
원래는 나머지를 빼주어야 하지만 modulo-2에서는 덧셈과 뺄샘이 같은 연산이라서 그냥 더해준것이다.
이렇게 만들어진 T(x)는 g(x)로 나누어 떨어진다.
• Sender sends T(x)
• Receiver receives T’(x)
• Receiver calculates T’(x) / g(x)
• If the remainder is zero, the receiver presumes
T(x) = T’(x) (no error)
나누어 떨어지면 에러가 아니지만 나누어 떨어지지 않으면 에러라고 취급한다.
• When does CRC fail to detect an error?
• An error has occurred but, still the modified codeword T’(x) is divisible by g(x)
-> error detection fails
• T’(x) = T(x) + e(x)
– e(x) is the error
– If T(x) + e(x) is divisible by g(x), then the receiver thinks the codeword is correctly received
• Error detection performance of CRC depends on g(x)
그런데 막상 오류가 발생해서 T'(x)가 되었는데 이게 우연하게 g(x)로 나누어 떨어지는 상황이 생기면 오류를 검출하지 못한 상황이 되는 것이다.
여기에서 생각해 볼 수 있는 것은 T(x)에서 오류가 발생해서 T'(x)가 되었는데도 g(x)로 나누어 질 수 있다는 것을 수정하기 위해 선택된 g(x)를 복잡하게 만들 수 있다. 대신에 g(x)의 차수가 높아진다.
Performance of CRC
• Suppose the divisor has x^0 term, and has at least one
other term
– e.g. g(x) = x^2 + 1
• Then, all 1-bit errors can be detected
• Why?
예를 들어 어떤 divisor가 x^0이 있고 다른 항이 더 있다면 1-bit 에러가 반드시 detect 될 수 있다.
1bit error는 다항식으로 표현시 x^2이 된다. 만약에 1011을 보냈는데 1001이 왔다면 에러가 0010이 된다. 즉 x가 된다. 1bit에러가 날 경우 다항식으로 표현하면 e(x) = 1, x, x^2, x^3, x^4 인데 어떤것도 x^2+1로 나누어 떨어지지 않는다. 따라서 1bit error detect가 가능하다.
• Which of the following divisors can detect all 1-bit errors?
• a. x + 1 -> 이중에서 얘만가능
• b. x3
• c. 1
• If degree of the polynomial is n
– detects all burst errors of size n or smaller
– If size of the burst is n+1, the error can be detected with probability 1– (1/2)^(n-1)
– If size of the burst is larger than n+1, the error can be detected with probability 1 – (1/2)^n
Burst Error
• Multiple bits are corrupted
• Length of the burst error: from the first corrupted bit
to the last corrupted bit
Performance of CRC
• Suppose the divisor is x^6 + 1
– All burst errors with size 6 or less are detected
– If the length of the burst is 7, then error detection probability is 31/32
– If the length of the burst is 8 or higher, then error detection probability is 63/64
• Powerful!
• CRC divisors used in practic
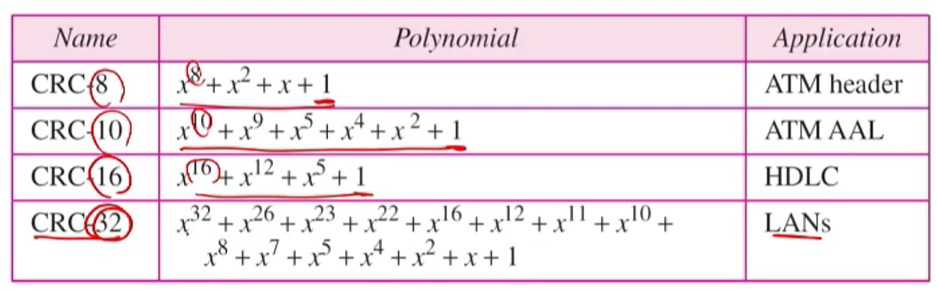
실재 현직에서 쓰는 CRC는 상당히 복잡하다.
