1차원 유형
키워드
1차원 유형의 문제는 점화식이 확실하게 결정되어 있기 때문에 점화식만 구해낸다면 쉽게 문제를 풀어낼 수 있다.
알고리즘
- 마지막에 값이 올때의 독립된 경우를 구한다.
- 점화식을 구한다.
- 초기화를 한다.
문제
1003 피보나치함수
그냥 풀면 시간 없는 문제
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <cstdlib>
#include <cstring>
#include <functional>
#define ll long long
#define len 2001
using namespace std;
int d[len] = {0};
int fibo(int n) {
if (n <= 1) {
return d[n];
}else if (d[n]) return d[n];
return d[n]=fibo(n - 1) + fibo(n - 2);
}
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
d[0] = 1;
d[1] = 1;
while (t--) {
int n;
cin >> n;
if (n == 0) cout << "1 0" << '\n';
else if (n == 1) cout << "0 1" << '\n';
else {
fibo(n);
cout << d[n - 2] << ' ' << d[n - 1] << '\n';
}
}
}9461 파도반 수업
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
ll d[100];
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
d[1] = d[2] = d[3] = 1;
for (int i = 4; i <= 100; ++i) {
d[i] = d[i - 2] + d[i - 3];
}
while (t--) {
int n;
cin >> n;
cout << d[n] << '\n';
}
}1차원 - 백트래킹
키워드
문제 처리 과정에서 나온 것을 출력하라는 게 추가로 요구된다. 보통 쉬운문제에다가 이거 하나 붙이면 어려워진다.
그냥 백트래킹 할 줄 알면 쉽게 풀린다.
문제
12852 1로 만들기 2
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
int d[1000001];
int p[1000001];
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
memset(d, -1, sizeof(d));
d[1] = 0;
p[1] = 0;
d[2] = 1;
p[2] = 1;
for (int i = 3; i <= t; ++i) {
d[i] = d[i - 1] + 1;
p[i] = i-1;
if (i % 2 == 0 && d[i / 2] + 1 < d[i]) {
d[i] = d[i / 2] + 1;
p[i] = i / 2;
}
if (i % 3 == 0 && d[i / 3] + 1 < d[i]) {
d[i] = d[i / 3] + 1;
p[i] = i / 3;
}
}
cout << d[t] << '\n';
while (p[t] != 0) {
cout << t << ' ';
t = p[t];
}
cout << "1" << '\n';
}2차원 유형
키워드
알 수 없는 것은 DP에서 가장 중요한 정보이다.
이때도 유형을 크게 4가지로 나누어 볼 수 있는데
알 수 없는 값이(임의의 값) 고정된 값으로 제공된 경우와 제공되지 않는 경우이다.
- 임의의 값이 유동적
1) 경우의 수 : 점프 점프 DP
2) 최대, 최소 : 1,2 차원 점화식 DP - 임의의 값이 고정적
1) 경우의 수 :
2) 최대, 최소 : 퇴사DP
문제
2차원 DP - 이친수(불연속) 계열
키워드
문제 내부에 연속되어 나타나서는 안되다는 조건을 가지고 나타나는 계열의 문제들로 이를 이친수 혹은 불연속 문제라고 부르겠다.
알고리즘
2차원 DP로 풀어야 하며 점화식 D[n][i] 에서 n은 n자리까지의 값이고 i는 마지막수를 의미한다.
여기에서 키포인트는 지금까지 세워온 DP 점화식중에서 일부를 사용하지 않는 것에 있다.
문제
2193 이친수
쉽게 설명하여서 1이 연속으로 두번 들어가지 않는 연속된 0과 1의 숫자 나열을 찾아내라는 문제이다.
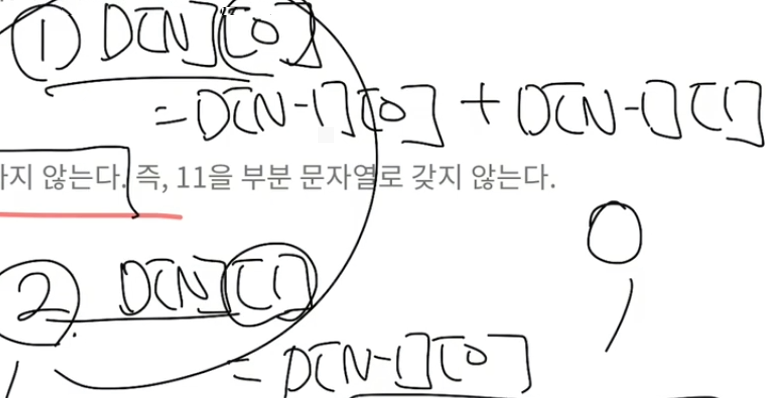
그렇기 때문에 1이 연속으로 두번 오는 경우를 제외하고 2차원 DP를 구성하면 된다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
vector<vector<ll>> d(91, vector<ll>(2, 0));
int a[10001];
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
d[1][0] = 0;
d[1][1] = 1;
for (int i = 2; i <= t; ++i) {
d[i][0] = d[i - 1][0] + d[i - 1][1];
d[i][1] = d[i - 1][0];
}
cout << d[t][0] + d[t][1] << '\n';
}그런데 이친수는 문제가 특이하게도 경우가 2가지 밖에 없기 때문에 2차원 DP로 풀지 않아도 된다.
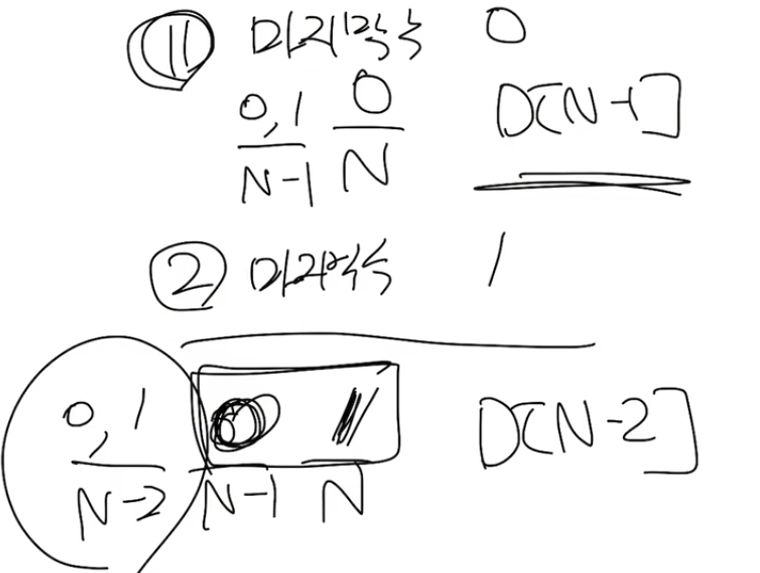
마지막에 0이 오는 경우 앞에 올 수 있는 경우는 0과 1이다.
반면 마지막에 1이 오는 경우 앞에 올 수 있는 경우는 0뿐이기 때문에 마지막에 1이 오는 것 전전의 값을 생각해 보아야 한다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
ll d[91];
int a[10001];
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
d[1] = 1;
d[2] = 1;
for (int i = 3; i <= t; ++i) {
d[i] = d[i - 1] + d[i - 2];
}
cout << d[t] << '\n';
}2156 포도주 시식
비슷하게 포도주 시식을 하는 것의 경우의 수를 생각해 보면
d[n][i]에서 n은 n번째 잔을 마시는가 i는 몇번째 연속인가를 따지는 것이다.
이때 경우의 수에 따라 점화식을 세워보면
d[n][0] = max(d[n-1][0],d[n-1][1],d[n-1][2])
d[n][1] = d[n-1][0]+a[n];
d[n][2] = d[n-1][1]+a[n];
밖에 존재하지 않기 때문에 이를 그대로 코드로 옮기어 주면 쉽게 풀린다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
ll d[10001][3];
int a[10001];
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
for (int i = 1; i <= t; ++i) {
cin >> a[i];
}
d[1][0] = 0;
d[1][1] = a[1];
d[1][2] = 0;
for (int i = 2; i <= t; ++i) {
d[i][0] = max(d[i - 1][0], max(d[i - 1][1], d[i - 1][2]));
d[i][1] = d[i - 1][0] + a[i];
d[i][2] = d[i - 1][1] + a[i];
}
cout << max(d[t][0], max(d[t][1], d[t][2])) << '\n';
}하지만 이 문제도 이친수와 비슷하게 나올 수 경우가 정해져 있기 때문에 이를 이용하여서 문제를 풀어 줄 수 있다.

마지막에 몇 번 연속으로 먹었는지에 따라 경우의 수가 갈리는데 그 수가 한정적이기 때문에 이것에 대해 간단한 알고리즘을 구현할 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
ll d[10001];
int a[10001];
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
for (int i = 1; i <= t; ++i) {
cin >> a[i];
}
for (int i = 1; i <= t; ++i) {
d[i] = d[i - 1];
if (d[i] < d[i - 2] + a[i]) d[i] = d[i - 2] + a[i];
if (d[i] < d[i - 3] + a[i] + a[i - 1]) d[i] = d[i - 3] + a[i] + a[i - 1];
}
cout << d[t] << '\n';
}2579 계단 오르기
한 번 계단을 오른것인지 두 번 계단을 오른것인지 알 수 없으며 추가적으로 올라간 계단의 값만큼 값이 크게 변화하기 때문에 2차원 DP로 경우의 수를 나누어 주어야 한다.
다행인 거은 초기화하기 쉽고
점화식을 찾기 쉽기 때문에 2차원 DP 문제로 바로 풀 수 있다.
또 다른 풀이법이 조재할 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
int main(void) {
freopen("input.txt", "r", stdin);
int a[301] = { 0 };
int d[301][2] = { 0 };
int t;
scanf("%d", &t);
for (int i = 1; i <= t; ++i) {
scanf("%d", &a[i]);
}
int cnt = 0;
d[1][1] = a[1];
d[2][1] = a[1] + a[2];
d[2][2] = a[2];
for (int i = 3; i <= t; ++i) {
d[i][1] = d[i - 1][2] + a[i];
d[i][2] = max(d[i - 2][1] + a[i], d[i - 2][2] + a[i]);
}
cout << max(d[t][1],d[t][2]) << '\n';
}기타문제
1463 1로 만들기
문제의 유형을 보면 점화식을 먼저 주어준 것을 확인할 수 있다.

이렇게 점화식을 주어졌다고 보이면 확실한 DP문제이다. 많지 않아서 문제이지.
import sys
#sys.stdin = open("input.txt","r")
input = sys.stdin.readline
d=[0]*1000001
t = int(input())
d[2]=1
for i in range(3,t+1):
d[i]=d[i-1]+1
if(i%2==0 and d[int(i/2)]+1<d[i]):
d[i]=d[int(i/2)]+1
if(i%3==0 and d[int(i/3)]+1<d[i]):
d[i]=d[int(i/3)]+1
print(d[t])11726 2xn 타일링
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
d=[0]*1001
mod = 10007
t = int(input())
d[1] = 1
d[2] = 2
for i in range(3,t+1):
d[i]=(d[i-1]+d[i-2])%mod
print(d[t]%mod)11727 2xn 타일링 2
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
d=[0]*1001
mod = 10007
t = int(input())
d[1] = 1
d[2] = 3
for i in range(3,t+1):
d[i]=(d[i-1]+d[i-2]*2)%mod
print(d[t]%mod)9095 1,2,3 더하기
이 문제에서 참고해야 하는 것은 순서를 신경쓴다는 점이다. 순서가 명확하게 고정되어 있는 이후의 문제와 다르게 순서가 다르면 다른 경우로 취급한다. 이러한 점도 바로 DP로만 풀 수 있는 점이다.
꼭 신경쓰자. 순서가 달라고 하나의 경우로 취급하는 것은 DP에서 나오는 문제이다.
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
d=[0]*12
t = int(input())
d[1] = 1
d[2] = 2
d[3] = 4
for i in range(4,12):
d[i] = d[i-1]+d[i-2]+d[i-3]
for i in range(t):
s = int(input())
print(d[s])11052 카드 구매하기
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t= int(input())
p=list(map(int,input().split()))
d=[0]*1001
p=[0]+p
d[1] = p[1]
for i in range(2,t+1):
for j in range(1,i+1):
if(d[i]<d[i-j]+p[j]):
d[i]=d[i-j]+p[j]
print(d[t])16194 카드 구매하기 2
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t= int(input())
p=list(map(int,input().split()))
d=[-1]*1001
p=[0]+p
d[0]=0
d[1] = p[1]
for i in range(2,t+1):
for j in range(1,i+1):
if(d[i]==-1 or d[i]>d[i-j]+p[j]):
d[i]=d[i-j]+p[j]
print(d[t])15999 1,2,3 더하기 5
import sys
sys.stdin = open("input.txt","r")
input=sys.stdin.readline
t = int(input())
d=[[0]*4 for _ in range(100001)]
mod = 1000000009
d[1][1]=d[2][2]=1
d[3][1]=d[3][2]=d[3][3]=1
for i in range(4,100001):
d[i][1]=(d[i-1][2]+d[i-1][3])%mod
d[i][2]=(d[i-2][1]+d[i-2][3])%mod
d[i][3]=(d[i-3][1]+d[i-3][2])%mod
for _ in range(t):
s = int(input())
print((d[s][1]+d[s][2]+d[s][3])%mod)10844 쉬운 계단 수
import sys
sys.stdin = open("input.txt","r")
input=sys.stdin.readline
t = int(input())
d=[[0]*10 for _ in range(101)]
mod = 1000000000
for i in range(1,10):
d[1][i]=1
for i in range(2,t+1):
d[i][0]=(d[i-1][1])%mod
d[i][9]=(d[i-1][8])%mod
for j in range(1,9):
d[i][j]=(d[i-1][j-1]+d[i-1][j+1])%mod
print((d[t][0]+d[t][1]+d[t][2]+d[t][3]+d[t][4]+d[t][5]+d[t][6]+d[t][7]+d[t][8]+d[t][9])%mod)2193 이친수
import sys
sys.stdin = open("input.txt","r")
input=sys.stdin.readline
t = int(input())
d = [[0]*2 for _ in range(91)]
d[1][1] =1
for i in range(2,t+1):
d[i][0]=(d[i-1][1]+d[i-1][0])
d[i][1]=(d[i-1][0])
print(d[t][0]+d[t][1])11053 가장 긴 증가하는 부분 수열
import sys
sys.stdin = open("input.txt","r")
input=sys.stdin.readline
t = int(input())
a=list(map(int,input().split()))
d=[0]*t
for i in range(t):
d[i]=1
for j in range(i):
if(a[j]<a[i] and d[i]<d[j]+1):
d[i]=d[j]+1
print(max(d))14002 가장 긴 증가하는 부분 수열 4
백트래킹이 되는 배열은 가급적 -1로 초기화
import sys
sys.stdin = open("input.txt","r")
input=sys.stdin.readline
t = int(input())
a=list(map(int,input().split()))
d=[0]*t
r=[-1]*t
for i in range(t):
d[i]=1
for j in range(i):
if(a[j]<a[i] and d[i]<d[j]+1):
d[i]=d[j]+1
r[i]=j
print(max(d))
def go(p):
if(p==-1):
return
go(r[p])
print(a[p],end=' ')
go(d.index(max(d)))1912 연속합
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
a = list(map(int,input().split()))
d = [0] * t
for i in range(t):
d[i] = a[i]
if(d[i] < d[i-1] + a[i]):
d[i] = d[i-1] + a[i]
print(max(d))1699 제곱수의 합
우선 그리디하게 문제를 풀었는데 런타임 에러 나왔다 ㅠ
import sys
import math
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
c=0
while(t>0):
for i in range(int(math.sqrt(t)),-1,-1):
if(t-i**2>=0):
t-=i**2
c+=1
break
print(c)제곱수로 움직여야지 문제를 풀 수 있었다.
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
d=[-1]*(t+1)
d[0]=0
d[1] = 1
for i in range(2,t+1):
j=1
while j*j<=i:
if(d[i]==-1 or d[i-j**2]+1<d[i]):
d[i]=d[i-j*j]+1
j+=1
print(d[t])2225 합분해
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
n,k= map(int,input().split())
d=[[0]*(n+1) for _ in range(k+1)]
mod =1000000000
d[0][0]=1
for i in range(1,k+1):
for j in range(n+1):
for l in range(j+1):
d[i][j]+=d[i-1][j-l]
d[i][j]%=mod
print(d[k][n]%mod)15988 1,2,3 더하기 3
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
mod = 1000000009
d = [0] * 1000001
d[1] =1
d[2] = 2
d[3] = 4
for i in range(4,1000001):
d[i] = (d[i - 1] + d[i - 2] + d[i - 3]) % mod
for i in range(t):
s = int(input())
print(d[s])1149 RGB 거리
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
p = [list(map(int,input().split())) for _ in range(t)]
d = [[0] * 3 for _ in range(t)]
d[0][0] = p[0][0]
d[0][1] = p[0][1]
d[0][2] = p[0][2]
for i in range(1,t):
d[i][0] = min(d[i - 1][1:3]) + p[i][0]
d[i][1] = min(d[i - 1][::2]) + p[i][1]
d[i][2] = min(d[i - 1][0:2]) + p[i][2]
print(min(d[t - 1][0:3]))1309 동물원
동물원과 같이 경우의 수가 제한적인 경우에는 3차원 DP를 2차원 DP로 줄일 수 있다.
이는 앞에서 보았던 이친수와도 비슷한 유영이라고 생각할 수 있다.
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
d=[[0]*3 for _ in range(t)]
mod = 9901
d[0][0]=d[0][1]=d[0][2]=1
for i in range(1,t):
d[i][0]=(d[i-1][0]+d[i-1][2]+d[i-1][1])%mod
d[i][1]=(d[i-1][0]+d[i-1][2])%mod
d[i][2]=(d[i-1][0]+d[i-1][1])%mod
print((d[t-1][0]+d[t-1][1]+d[t-1][2])%mod)11057 오르막 수
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
d=[[0]*10 for _ in range(t+1)]
mod = 10007
for i in range(0,10):
d[1][i]=1
for i in range(2,t+1):
for j in range(0,10):
for k in range(0,10):
if(j-k>=0):
d[i][j]+=d[i-1][j-k]
d[i][j]%=mod
ans = 0
for i in range(0,10):
ans+=d[t][i]
ans%=mod
print(ans)9465 스티커
동물원과 비슷한 문제라고 보인다.
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
d=[[0]*200001 for _ in range(3)]
for i in range(t):
s = int(input())
a = list(list(map(int,input().split())) for _ in range(2))
d[0][0]=a[0][0]
d[1][0]=a[1][0]
for j in range(1,s):
d[0][j]=max(d[1][j-1],d[2][j-1])+a[0][j]
d[1][j]=max(d[0][j-1],d[2][j-1])+a[1][j]
d[2][j]=max(d[0][j-1],d[1][j-1],d[2][j-1])
print(max(d[0][s-1],d[1][s-1],d[2][s-1]))2156 포도주 시식
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
a = list(int(input()) for _ in range(t))
d = [[0]*3 for _ in range(t)]
d[0][1] = a[0]
for i in range(1, t):
d[i][0] = max(d[i-1][0],d[i-1][1],d[i-1][2])
d[i][1] = d[i-1][0]+a[i]
d[i][2] = d[i-1][1]+a[i]
print(max(d[t-1][0:3]))1932 정수 삼각형
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
a = [0]+list(list(map(int,input().split())) for _ in range(t))
d = [[0]*t for _ in range(t+1)]
d[1][0] = a[1][0]
for i in range(2, t+1):
for j in range(0,i):
if(j==0): d[i][j]=d[i-1][j]+a[i][j]
elif(j==i-1): d[i][j]=d[i-1][j-1]+a[i][j]
else: d[i][j]=max(d[i-1][j-1],d[i-1][j])+a[i][j]
print(max(d[t][:]))11055 가장 큰 증가하는 부분 수열
import sys
#sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
a=list(map(int,input().split()))
d=[0]*t
for i in range(t):
d[i]=a[i]
for j in range(i):
if(a[j]<a[i] and d[j]+a[i]>d[i]):
d[i]=d[j]+a[i]
print(max(d))11054 가장 긴 바이토닉 부분 수열
두 번 구한 다음에 합친다.
13398 연속합 2 : 슬라이싱
그냥 숫자 하나 지우고 구하고 계속 반복하는데 걸리는 시간은 O(n^2)이 나오게 되기에 불가능하다.
두번 구한다음에 합치는 방식으로 하자
d[i] = i번째에서 끝나는 연속합
d2[i] = i번째에서 시작하는 연속합
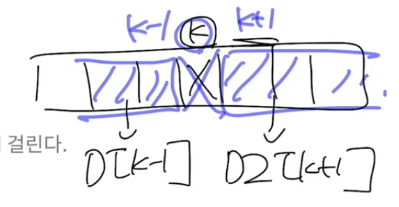
이 방식으로 k번째를 넣고나 뺀다면 k번째에서 나올 수 있는 모든 경우를 계산할 수 있다.
그래서 우선 d[i]와 d2[i]를 모두 계산한다음 i번째를 넣거나 뺏을때 최대가 나오는 경우를 나중에 따로 계산하는 슬라이싱 방법이 나온다.
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
a=list(map(int,input().split()))
d=[0]*t
d2=[0]*t
for i in range(t):
d[i]=a[i]
if(i==0): continue
if(d[i]<d[i-1]+a[i]): d[i]=d[i-1]+a[i]
for i in range(t-1,-1,-1):
d2[i]=a[i]
if(i==t-1): continue
if(d2[i]<d2[i+1]+a[i]): d2[i]=d2[i+1]+a[i]
max = d[0]
for i in range(1,t):
if(max<d[i]): max=d[i]
for i in range(1,t-1):
if(max<d[i-1]+d2[i+1]): max=d[i-1]+d2[i+1]
print(max)2133 타일 채우기
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
#!/usr/bin/python3
t = int(input())
d=[0]*(t+1)
d[0]=1
for i in range(2,t+1,2):
d[i]=d[i-2]*3
for j in range(i-4,-1,-2):
d[i]+=d[j]*2
print(d[t])17404 RGB 거리2
상당히 빡샌무제였다. 처음과 마지막이 같으면 안되는 문제라니 ㅎㄷㄷ
import sys
sys.stdin = open("input.txt","r")
input = sys.stdin.readline
t = int(input())
a=[[0,0,0]]+list(list(map(int,input().split())) for _ in range(t))
d=[[0]*3 for _ in range(t+1)]
ans = 1000*1000+1
for i in range(3):
for j in range(3):
if(i==j): d[1][i]=a[1][i]
else: d[1][j]=1000*1000+1
for j in range(2,t+1):
d[j][0]=min(d[j-1][1],d[j-1][2])+a[j][0]
d[j][1]=min(d[j-1][0],d[j-1][2])+a[j][1]
d[j][2]=min(d[j-1][0],d[j-1][1])+a[j][2]
for j in range(3):
if(i==j): continue
else: ans=min(ans,d[t][j])
print(ans)
