02. Number Systems(수의 세계)

이제 컴퓨터가 데이터를 받을 수 있도록 데이터 변환방식에 대해서 생각해 보도록하겠다.

Number System은 대표적인 2,8,16 진수의 꼴로 데이터를 표현하는 방식으로 0과 1만의 데이터를 읽는 컴퓨터에 이어서 매우 필요한 방식이다.

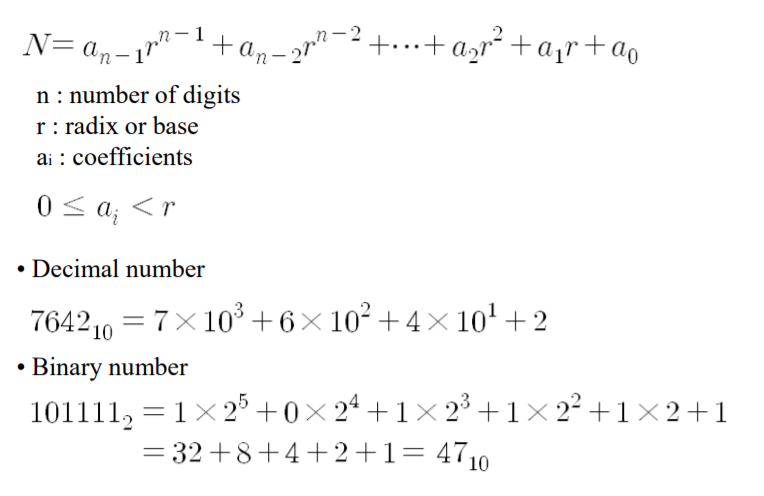
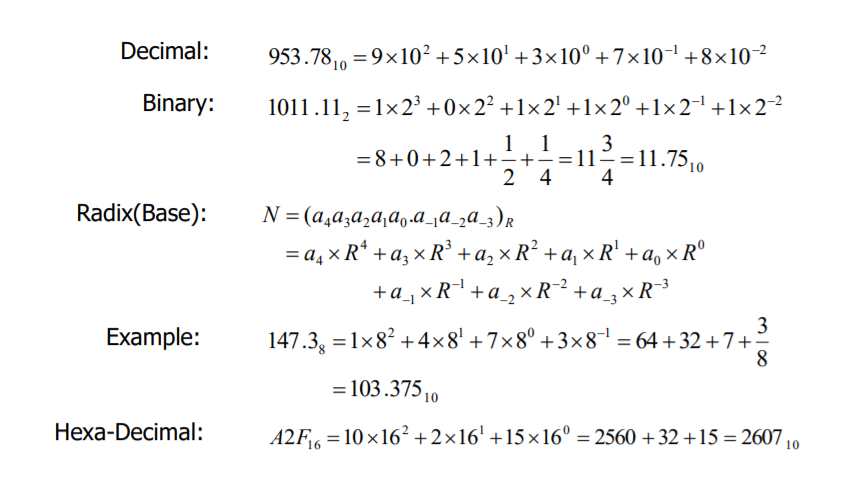
10진수 / 2진수 / 실수 / 예시 / 16진수 꼴로 예시를 들어 보았다.

또한 2진수/8진수/16진수에서 다른 진수로 가는 과정은 단순히 2진수로 변환하는 중간과정을 거친 후 갯수별로 비트를 나누기만 하면 되기 때문에 큰 어려움은 없다.

2.5. Representation of negative numbers : signed numbers(2진수 정수 연산과 보수)

2진수의 음수 표현 방법 중 하나는 sign magnitude(부호-절댓값) 방법이다.

최상위의 비트가 0이면 양수 1이면 음수를 의미하며
-(2^(n-1) - 1) ~ (2^(n-1) - 1) 까지 범위의 데이터를 표현할 수 있다.

2. Representation of negative numbers : 2's complement

또다른 2진수의 음수 표현 방법 중 하나는 2's complement(2의 보수) 방법이다. 주로 컴퓨터에서 사용하는 방식으로 이를 통해 뺄샘이라는 연산 없이 덧셈 연산만으로도 수도 없이 많은 비트들의 연산을 수행할 수 있다.

이 방법은 원래는 2^n-a 한다음 2진수로 바꾸지만 사용이 어렵다.
그렇기 때문에 다음의 과정을 거친다.

1. 2진수의 값으로 바꾼다.
2. 1의 보수를 취한다.
3. 1을 더한다.
   

-(2^(n-1)) ~ (2^(n-1) - 1) 까지 범위의 데이터를 표현할 수 있다.

중요한 것은 이 방식을 통해서 기존 더하기와 뺄샘 방법 모두 존재했던 것을 오로지 덧셈만으로도 뺼샘 연산도 가능하도록 만들 수 있다.

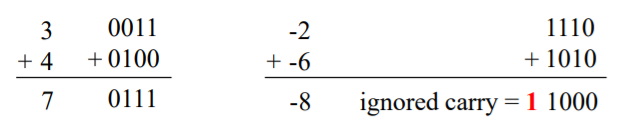
덧샘자체는 그냥 하면 된다.

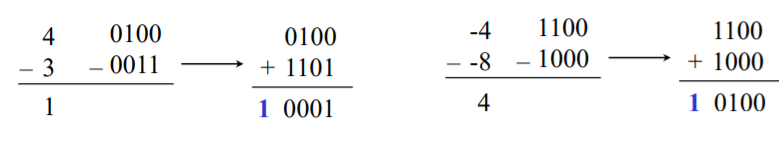
뺄샘은 2의 보수를 취한다음 더하면 된다.

단 덧셈중에 overflow가 날 수도 있다.

BCD 코드