[알고리즘 스터디] 정렬

일단 c++에서는 기본적으로 sort 함수를 제공하고 있다!

#include <algorithm>

sort(arr, arr+n);

sort(v.begin(), v.end()); //벡터의 경우

sort(v.begin(), v.end(), compare); //사용자 정의 함수 사용

sort(v.begin(), v.end(), greater<자료형>()); //내림차순 (Descending order)

정렬 알고리즘

1. 선택정렬

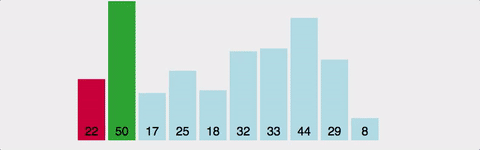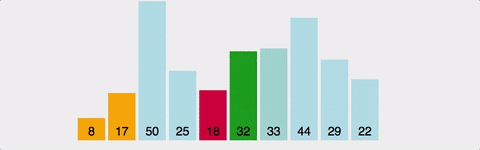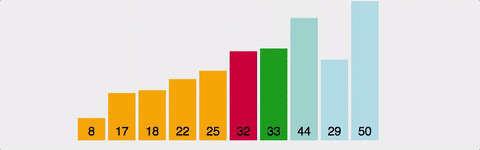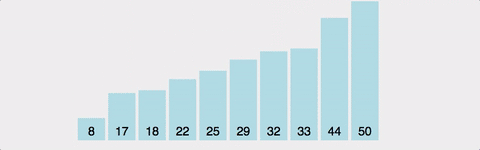
• 선택정렬은 앞쪽부터 정렬해나가는 방식이다.
• 주어진 배열에서 가장 최소값을 찾고 그 값을 맨 앞의 값과 위치를 바꾸면서 정렬해나간다.
• 즉, 정렬에서 최소값을 "선택"하는 과정을 반복하는 알고리즘이다.
  
• 장점 : 교환 횟수가 적고 구현이 간단
• 단점 : 시간이 오래 걸림
• 시간복잡도 :
  평균 O(N^2)
  최선 O(N^2)
  최악 O(N^2)

2. 버블정렬

• 첫번째 원소부터 인접한 원소와 비교하며 자리를 바꾸면서 맨 끝부터 정렬하는 방식
• 가장 큰 값을 뒤로 보내며 뒤쪽부터 정렬됨
• 정렬되는 모습이 마치 물 속에서 올라오는 물방울 같아서 버블정렬
  
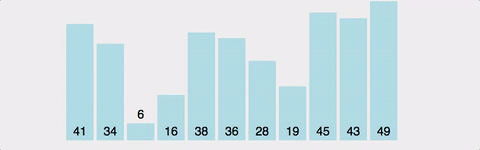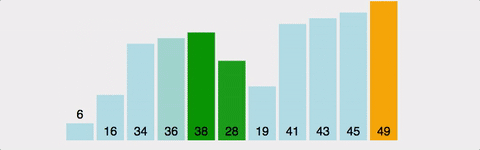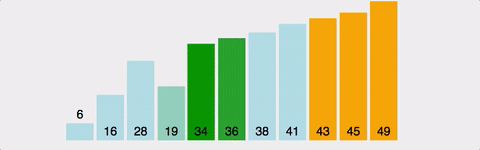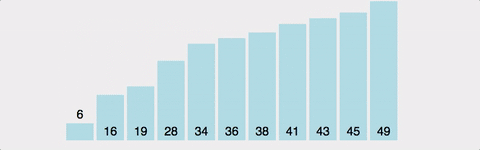
• 장점 : 구현이 간단
• 단점 : 하나씩 비교하므로 시간 오래 걸림
• 시간복잡도 :
  평균 O(N^2)
  최선 O(N)
  최악 O(N^2)
  
  

3.삽입정렬

• i번째 원소를 정렬된 상태의 앞부분과 비교하여 적절한 위치에 삽입
• i-1번째까지는 모두 정렬된 상태여야하고 삽입하려는 i번째 원소를 0부터 i-1번째 원소와 비교하여 적절한 위치에 삽입
  
• 장점 : 정렬된 상태일 수록 속도 빠름, 정렬된 값은 교환이 일어나지 않음
• 단점: 삽입을 구현해야 하므로 자료구조가 중요, 역순으로 정렬되었을 경우 완전 비효율적
• 시간복잡도 :
  평균 O(N^2)
  최선 O(N)
  최악 O(N^2)
  

4.병합정렬

• 배열을 작은 단위로 쪼개 정렬한 결과를 합쳐가며 전체를 정렬하는 방식
• 배열을 왼쪽 반, 오른쪽 반으로 분할해감
  
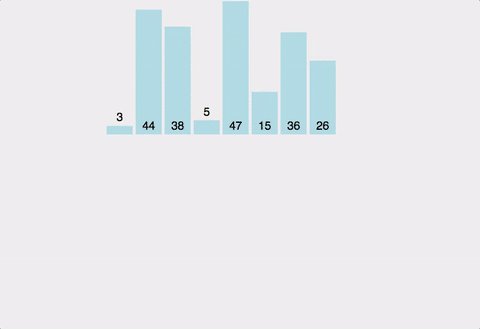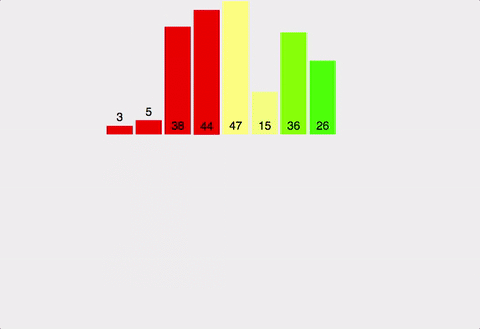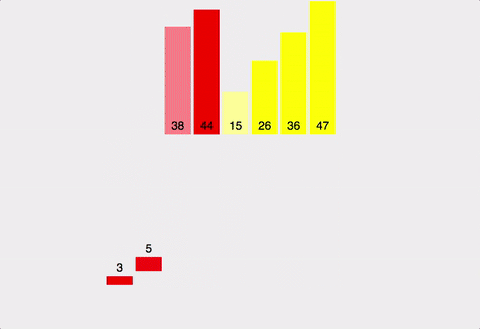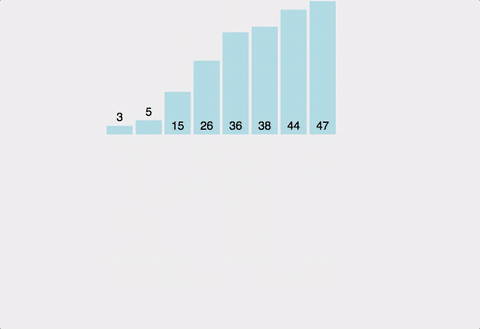
• 장점 : 항상 일정한 시간복잡도( O(NlogN) )를 가짐, 안정적이고 성능 좋음
• 단점 : 쪼갠 배열을 저장할 추가적인 메모리 공간이 필요
• 시간복잡도 :
  평균 O(NlogN)
  최선 O(NlogN)
  최악 O(NlogN)
  
  

5. 퀵정렬

• 하나의 피봇을 정해 피봇보다 작은 값은 왼쪽에, 큰 값은 오른쪽에 위치시킴.
• 왼쪽, 오른쪽 각각 다시 그 안에서 피봇을 정해 왼쪽, 오른쪽 나누는 과정 반복
  
  
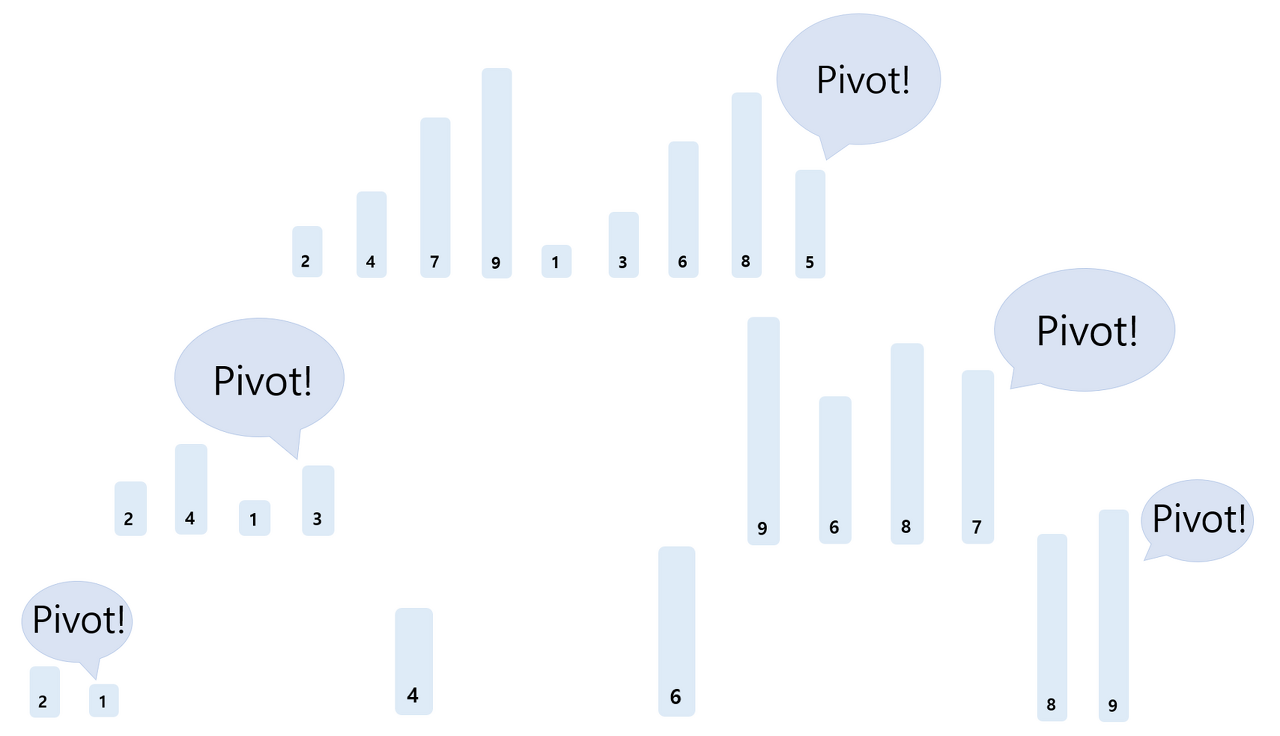
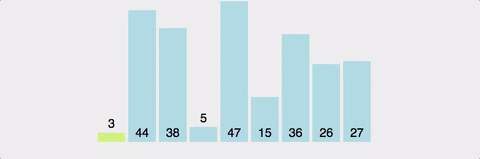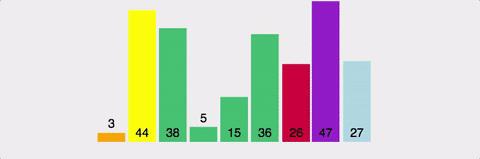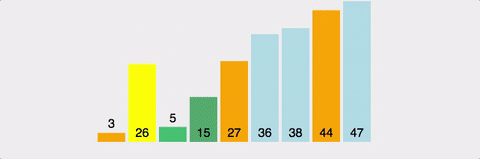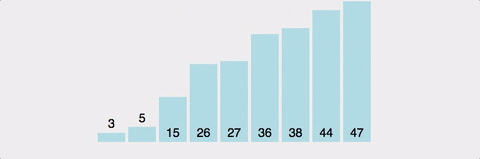
• 장점 : 평균 실행시간 빠름
• 단점 : 피봇을 어떻게 설정하는지에 따라 성능차이가 심하여 안정성이 좋지 않음
• 시간복잡도 :
  평균 O(NlogN)
  최선 O(NlogN)
  최악 O(N^2)

6.힙정렬

• 내림차순 정렬엔 max-heap 트리, 오름차순 정렬엔 min-heap 트리를 사용
  
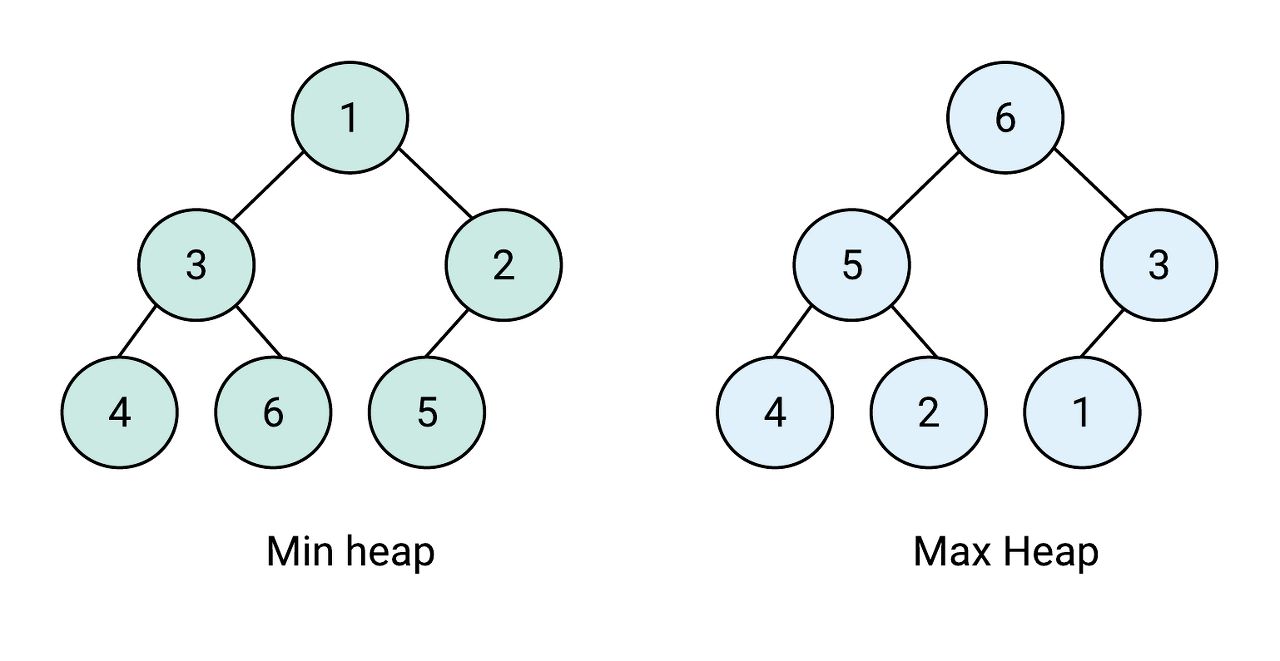
• 입력 배열로 먼저 최대 혹은 최소 힙 트리를 만들고 힙의 루트노드(최댓값 혹은 최솟값)를 빼내어 배열의 뒤쪽부터 넣는다. 이때 빈 루트노드 자리에는 힙의 마지막 원소가 들어간다.
• 장점 : 항상 같은 시간 복잡도
• 단점: 같은 시간복잡도를 가지는 다른 알고리즘과 비교하면 느린 편
• 시간복잡도 :
  평균 O(NlogN)
  최선 O(NlogN)
  최악 O(NlogN)