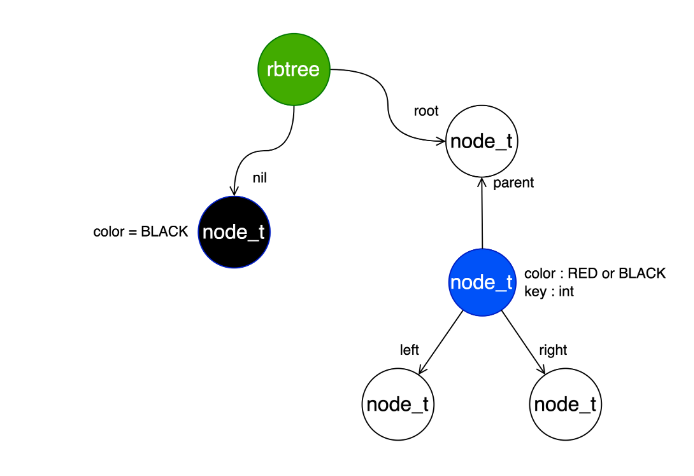
rbtree란?

red-black tree는 self-balancing binary search tree로서, 대표적으로 map, dictionary등 associative array를 구현하는 데 쓰이는 자료구조다. 복잡하지만, 실 사용에서 효율적이고, 삽입, 삭제 검색에서 최악의 경우에도 O(log n)의 상당히 우수한 실행 시간을 보인다(worst-case guarantees).

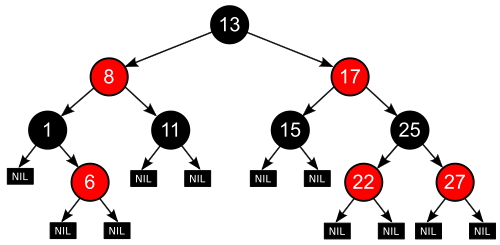
특성

#1 모든 노드는 RED / BLACK 이다
#2 루트 노드는 BLACK 이다.
#3 모든 NIL 노드(leaf node)는 BLACK 이다.
#4 노드가 RED면, 자녀는 BLACK 이다. 즉 RED는 연속할 수 없다.
#5 임의의 경로(자신을 제외)부터 자손 NIL까지 BLACK 개수는 동일하다. Black-height의 크기가 같다

동작

red-black tree는 binary search tree의 한 형태이기 때문에 탐색(read-only) 동작은 binary search tree와 동일하다. 그러나 삽입(insertion)과 삭제(removal)의 경우엔 binary search tree의 구현에 따른 동작만으로는 rbtree 특성을 만족하지 못한다.

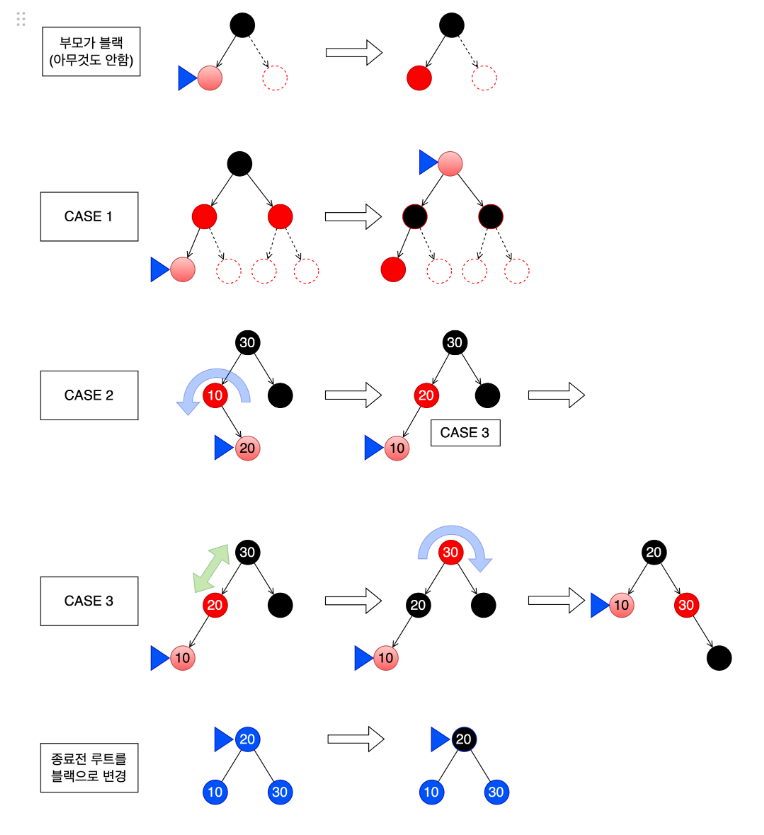
삽입

• 삽입 전 tree는 rbtree 속성을 만족한 상태이다.
• 삽입 방식은 일반적인 BST와 동일하나 삽입노드의 색은 항상 RED다.(#5를 유지하기 위해)
• 삽입 후 rbtree 속성 위반 여부를 확인한다.
• rbtree 속성을 위반했다면 재조정(insert-fixup)한다.
• rbtree 속성을 다시 만족시킨다.

node_t *rbtree_insert(rbtree *t, const key_t key) {
  // TODO: implement insert
  node_t *y = t->nil;
  node_t *x = t->root;
  node_t *z = (node_t *)calloc(1, sizeof(node_t));
  z->key = key;
  while(x != t->nil){
    y = x;
    if (z->key < x->key){
      x = x->left;
    }
    else{
      x = x->right;
    }
  }
  // 주석 만들기
  z->parent = y;
  if (y == t->nil){
    t->root = z;
  }
  else if (z->key < y->key){
    y->left = z;
  }
  else{
    y->right = z;
  }
  z->left = t->nil;
  z->right = t->nil;
  z->color = RBTREE_RED;		//삽입 노드는 RED
  // FIXUP
  while (z->parent->color == RBTREE_RED){
    if (z->parent == z->parent->parent->left){
      y = z->parent->parent->right;   
      if (y->color == RBTREE_RED){			//case 1
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;
      }
      else {
        if (z == z->parent->right){			//case 2
        z = z->parent;
        left_rotate(t, z);
      }
      z->parent->color = RBTREE_BLACK;		//case 3
      z->parent->parent->color = RBTREE_RED;
      right_rotate(t, z->parent->parent);
      }
    }
    else {									//좌우 대칭
      y = z->parent->parent->left;   
      if (y->color == RBTREE_RED){
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;
      }
      else {
        if (z == z->parent->left){
          z = z->parent;
          right_rotate(t, z);
        }
      z->parent->color = RBTREE_BLACK;
      z->parent->parent->color = RBTREE_RED;
      left_rotate(t, z->parent->parent);
      }
    }
  }
  t->root->color = RBTREE_BLACK;	//root node는 BLACK
  return z;
}

필자는 fixup을 한번에 처리했지만 구분하는 것이 더 가독성이 좋다.

삭제

• 삭제 전 tree는 rbtree 속성을 만족한 상태이다.
• 삭제 방식은 일반적인 BST와 동일하다.
• 삭제 후 rbtree 속성 위반 여부를 확인한다.
• rbtree 속성을 위반했다면 재조정(delete-fixup)한다.
• rbtree 속성을 다시 만족시킨다.

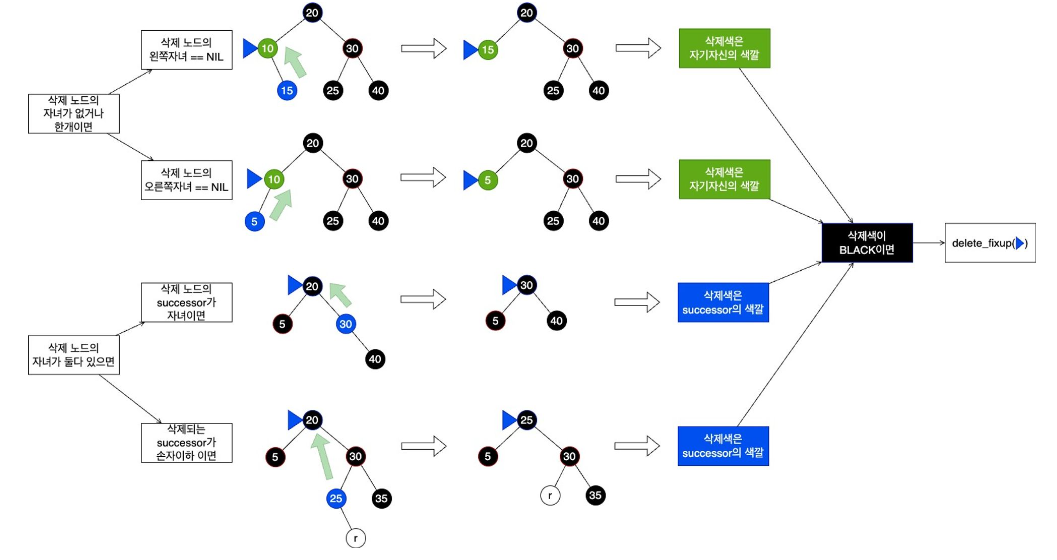
삭제 색이 RED이면, 어떠한 속성도 위반하지 않는다.

삭제 색이 BLACK이면, #2, #4, #5 속성을 위반할 수 있다.

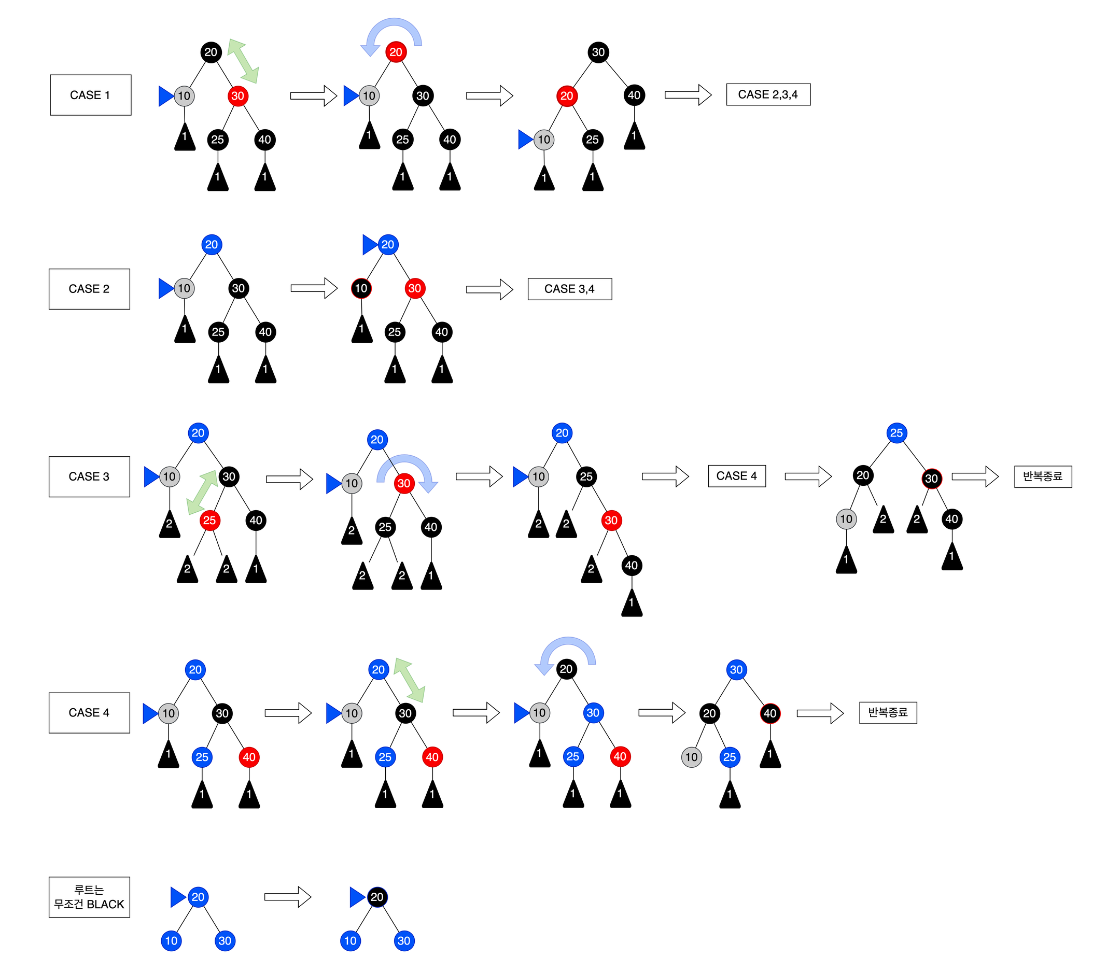
int rbtree_erase(rbtree *t, node_t *p) {
  // TODO: implement erase
  node_t *y = p;
  node_t *x;
  color_t y_original_color = y->color;
  if (p->left == t->nil){
    x = p->right;
    rb_transplant(t, p, p->right);
  }
  else if (p->right == t->nil){
    x = p->left;
    rb_transplant(t, p, p->left);
  }
  else {
    y = tree_successor(t, p);
    y_original_color = y->color;
    x = y->right;
    if (y->parent == p){
      x->parent = y;
    }
    else {
      rb_transplant(t, y, y->right);
      y->right = p->right;
      y->right->parent = y;
    }
    rb_transplant(t, p, y);
    y->left = p->left;
    y->left->parent = y;
    y->color = p->color;
  }
  // RB tree 특성 복구
  if (y_original_color == RBTREE_BLACK){
    while (x != t->root && x->color == RBTREE_BLACK){
      if (x == x->parent->left){
        node_t *w = x->parent->right;
        if (w->color == RBTREE_RED){
          w->color = RBTREE_BLACK;					//case 1
          x->parent->color = RBTREE_RED;
          left_rotate(t, x->parent);
          w = x->parent->right;
        }
        if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK){
          w->color = RBTREE_RED;					//case 2
          x = x->parent;
        }
        else {
          if (w->right->color == RBTREE_BLACK){		//case 3
            w->left->color = RBTREE_BLACK;
            w->color = RBTREE_RED;
            right_rotate(t, w);
            w = x->parent->right;
          }
        w->color = x->parent->color;				//case 4
        x->parent->color = RBTREE_BLACK;
        w->right->color = RBTREE_BLACK;
        left_rotate(t, x->parent);
        x = t->root;
        }
      }
      else {										//좌우 대칭
        node_t *w = x->parent->left;
        if (w->color == RBTREE_RED){
          w->color = RBTREE_BLACK;
          x->parent->color = RBTREE_RED;
          right_rotate(t, x->parent);
          w = x->parent->left;
        }
        if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK){
          w->color = RBTREE_RED;
          x = x->parent;
        }
        else {
          if (w->left->color == RBTREE_BLACK){
            w->right->color = RBTREE_BLACK;
            w->color = RBTREE_RED;
            left_rotate(t, w);
            w = x->parent->left;
          }
        w->color = x->parent->color;
        x->parent->color = RBTREE_BLACK;
        w->left->color = RBTREE_BLACK;
        right_rotate(t, x->parent);
        x = t->root;
        }
      }
    }
    x->color = RBTREE_BLACK;
  }
  free(p);
  return 0;
}

후기

개념적인 부분을 이해를 하고 코딩을 시작했다 생각했지만, 하면서 이해가 안되는 부분도 있었고 중간중간 막히기도 했다. 교재의 psuedo code가 없었다면 스스로의 힘으로는 구현할 수 없었을 것 같다.