Complete Guide to Medical Image Reconstruction

https://www.youtube.com/@AndrewJReader/videos
Image Reconstruction Basics
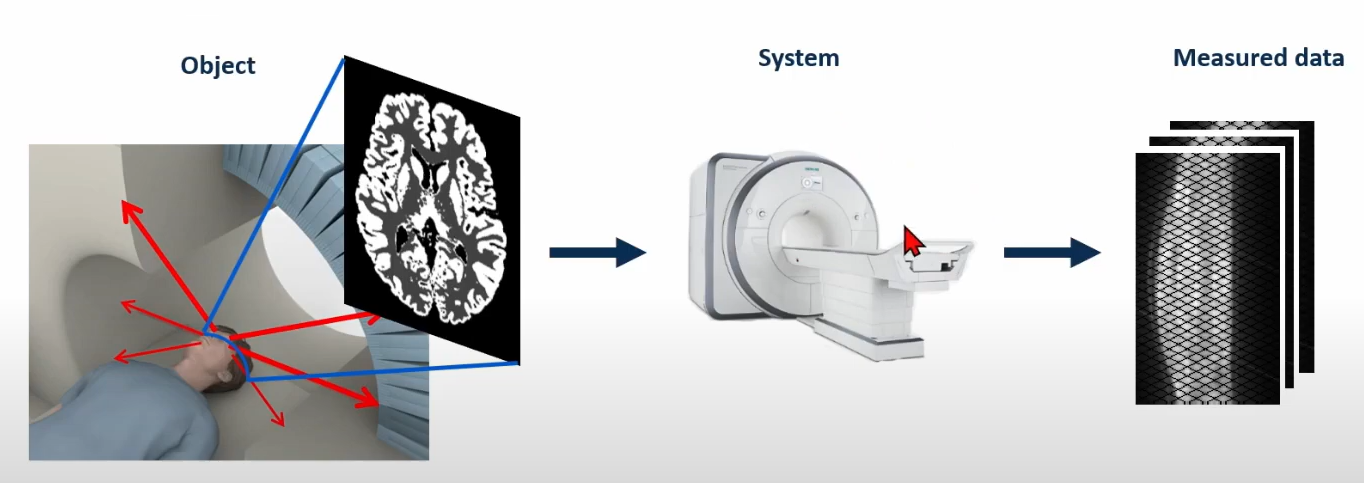
Object 를 연속적인 함수로 두고, 이를 시스템에 통과시키면 이산형 함수가 나온다.

원래의 object 는 연속적이지만, 실제 복구작업을 할 때는 절대 연속적인 데이터를 만들어낼 수 없다. 따라서, 이산형 구조를 사용하여 원 객체를 표현할 것인데, 이를 통해 parameter 의 수를 획기적으로 줄일 수 있다. 이란 위치에 있는 ground truth intensity 를 이라고 할 때, 이는 discrete representation 의 픽셀 값과 basis function 의 곱으로 나타낼 수 있다.
Note: basis function 은 linear regression 에서 더 나아가 x^2, gaussian 등의 basis 를 통해 복잡한 fitting 을 가능하게 해주는 개념. 포스팅 필요?
Object representation parameters (image)
Basis functions
이며, 여기에선 을 사용한다. 즉, continuous 한 function 을 하나의 픽셀로 전부 assign 하는 개념이다.
Objective
Image reconstruction 의 목표는 를 estimate 하기 위한 를 찾는 것이다
Manifold
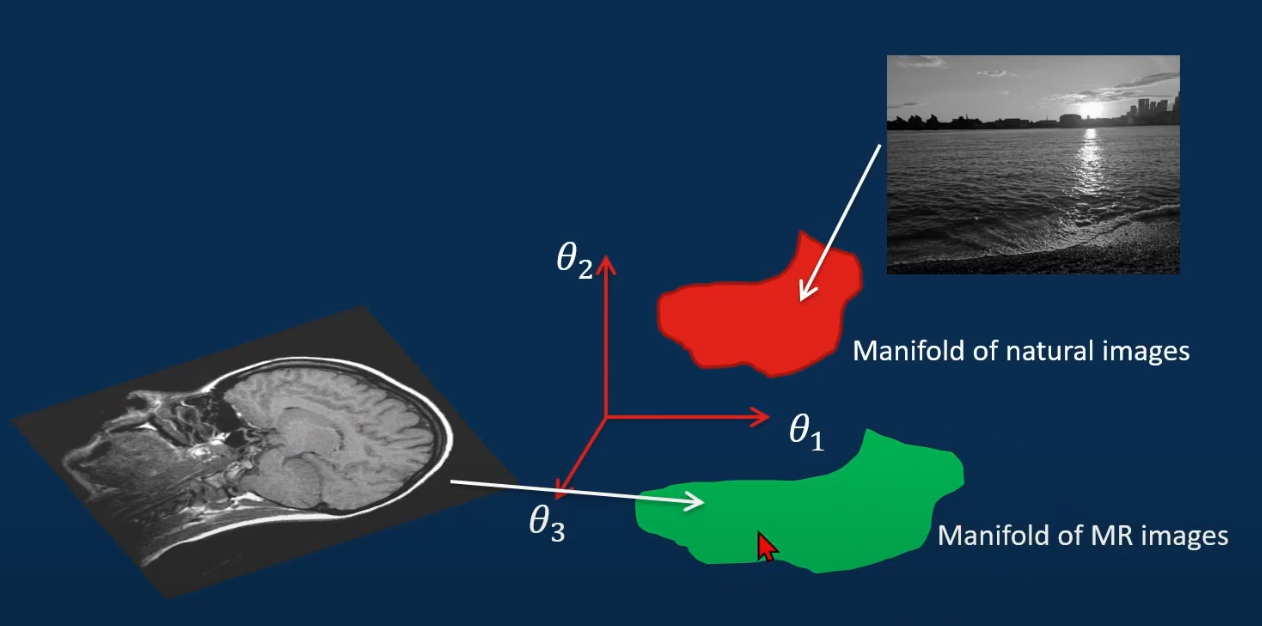
이미지 한장에 224 x 224 라고 하면, 이 이미지는 224 x 224 dimension (엄청나다..) 좌표계의 한 점으로 표현될 수 있다. 이 공간은 정말 정말 크지만, 비슷한 계열의 이미지 끼리는 묶여 있다는 직관을 가질 수 있다. 즉, 광활한 image space 에서 모든 강 사진이 빨간색 "manifold" 에 묶여 있다고 하면, MR 사진들은 초록색 "manifold" 에 속해 있다고 상상해 볼 수 있겠다.
Linear Systems and Diagonalization
PET data
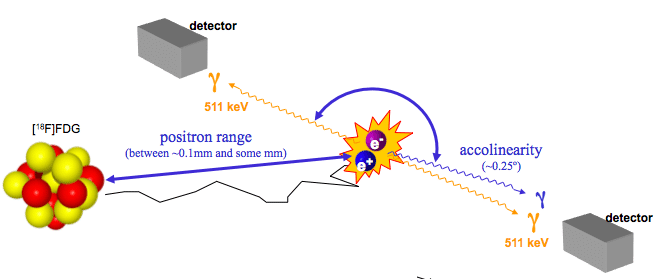
PET 영상은 18F 가 베타 붕괴를 거치며 positron 을 방출, 이것이 electron 과 만나며 annihilation 을 발생시키는데, 이로 인해 양방향으로 광자가 산란된다. 두 광자를 각각 검출기에서 탐지하게 되는데, 이 데이터를 어떻게 저장하는지 살펴보자.
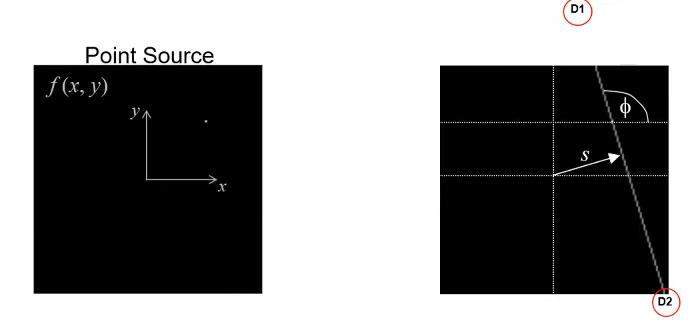
Point source 는 당연히 모르고, D1 와 D2 에서 광자가 검출되었다고 하자. 이 두 점을 이어준 뒤 x-y 좌표계의 x 축이 이 선과 일직선으로 맞추어지게 하는 각도 , 그리고 원점에서 부터 그 선의 거리를 라고 칭한다. 이에 따라, 세가지의 데이터 표현 방식이 가능하다.

- List
단순히 양 점, 에너지, 시간 등을 배열에 저장
- Backprojected image
두 점 사이를 이은 이미지를 저장
- Sinogram
위의 좌표계에 점으로 저장. 이 때 한 점마다 count 를 추가하는 것이기 때문에 histogram 을 그린다고 생각해도 됨.
Convolution

우리가 실제로 observe 하게 되는 PET 데이터를 g(r) 이라고 한다면, 이는 ground truth f(r') 을 point spread function (이하 psf) 와 convolution 한 결과로 모델링 할 수 있겠다. 즉, noisy 한 결과를 point spread function 을 통해 ground truth 를 복원하는 작업을 할 수 있다!
Image Reconstruction
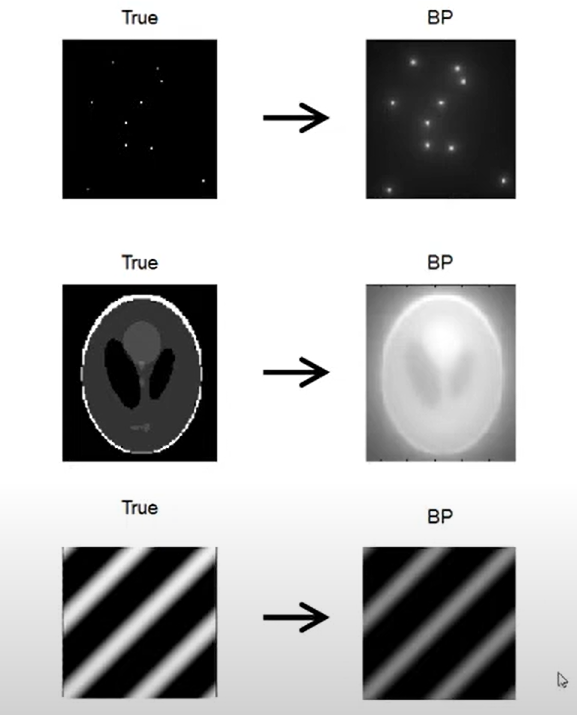
뭔가 이상한게 느껴지는가? 마지막 줄은 backprojection을 거치고 나도 이미지에 차이가 없고, intensity 의 scale만 차이가 있다!
Why Fourier basis?
Sinusoids are eigenfunctions of the convolution operator
Given g(x),
If S{} is an LSI / LTI system, then
We can extend this to Fourier basis, which is composed of sinusoidal functions!
