Introduction

A distribution (of shapes) of distributions (of actual points)

-> Given a cloud of points, which shape is this most likely?

달리말해, 저자들의 목표는 invertible parametrized transformation 을 학습하는 것이라고 한다.

-> 즉, 어떤 분포 (3D 가우시안 등) 에 대해 가역적인 변환을 학습하는 것.

왜 가역적이냐? 변환 과정을 보면 알 수 있는데, 변환 과정은 주어진 분포에서 몇 개의 점을 뽑은 뒤 그 점들을 움직이는 것으로 이루어져 있음. 따라서, 움직인 점들을 되돌려 놓으면 역변환이 됨.

Related Works

저자들은 포인트클라우드를 정해진 차원의 matrix 로 간주하는 것은 단점이 많다고 한다.

1. 모델이 생성할 수 있는 점의 수가 한계가 있음
2. Permutation invariance 가 깨짐
3. 그냥 autoencoder 의 loss, earth mover's distance 는 계산이 오래걸리고, Chamfer distance 는 marginally concentrated distrubution 에 bias 되는 문제가 있음.

Method

Continuous Normalizing Flow

3D 유클리드 공간의 벡터이며, generic prior distribution 에서 점들을 sample 한 뒤 특정한 모양을 따르게 변환해주는 field.

각 normalizing flow 는 latent variable (직접적으로 관찰되지 않는 변수) 로 parametrize 되며, 이는 모양에 해당하게 된다. 우리는 어떤 점의 분포 (Gaussian 이라든가...) 가 주어졌을 때, 그 분포가 특정한 모양을 띌 확률분포 (posterior) 을 직접적으로 알 수 없기 때문에, latent variable의 분포를 모델링 하는 것으로 대신하게 되는 것이다. 이를 알고 나면, 그 모양은 점이 어떻게 분포해 있는지만 알면 된다 (비행기는 비행기처럼~).

그렇게 하기 위해선 KL divergence 를 최소화 해야겠지...

Variational Autoencoder

간단하다.. 인코더와 디코더로 나누어져 있는데,

인코더: 데이터 x 를 받으면 hidden representation z 를 뱉음.

디코더: z 를 받아서 확률 분포의 parameter 을 뱉음, p(x|z)

에혀.. 그냥 잘 정리된 곳 가서 보자 --> 글, MIT 유튭.

Model

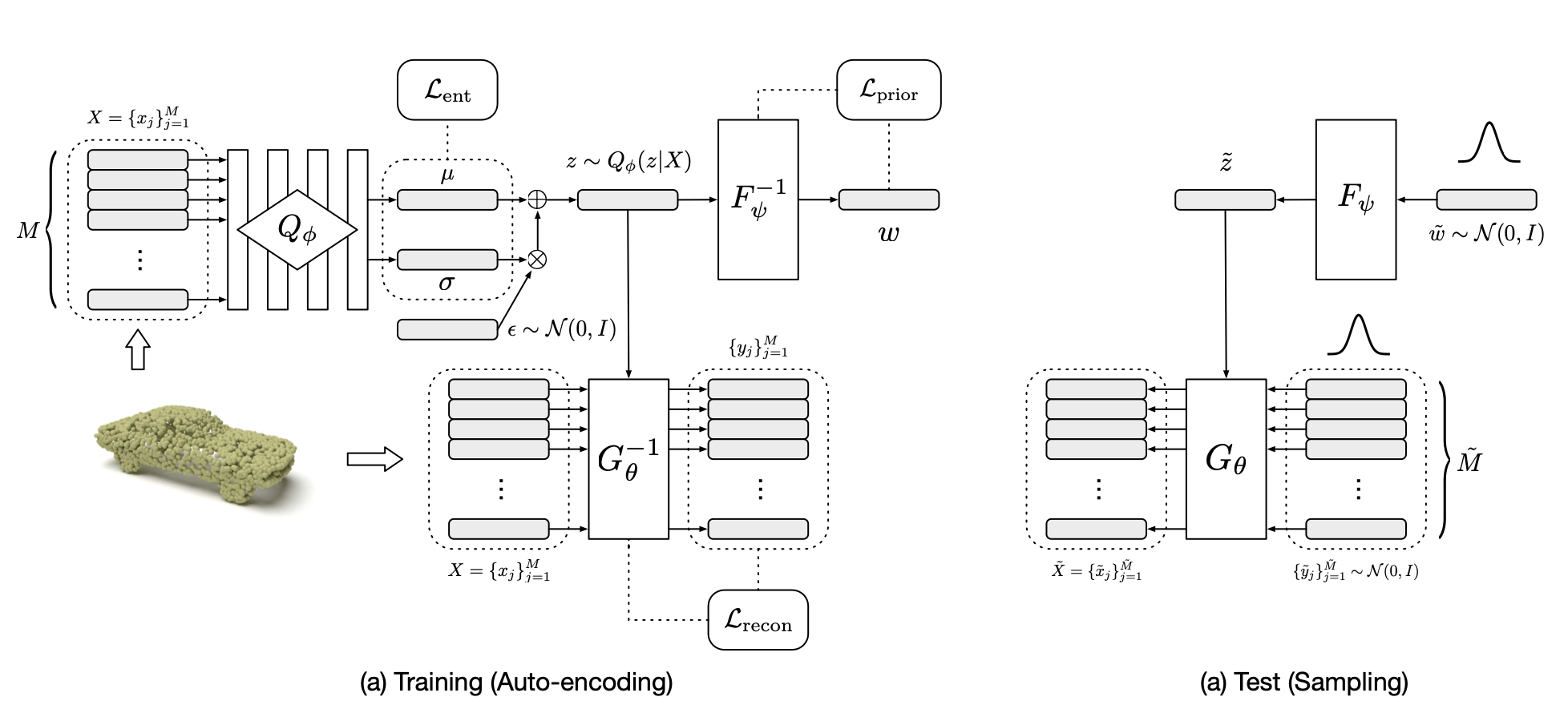
훈련 시에는,

Entropy loss: encoder 에서 포인트클라우드 (X) 를 받아 posterior 을 유추하고, 그 분포에서 shape representation z 를 뽑음. 이 분포와 실제 분포의 loss를 구함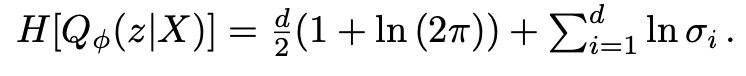

Prior loss: 사용한 CNF 를 inverse 해서 다시 z로부터 prior 분포를구함.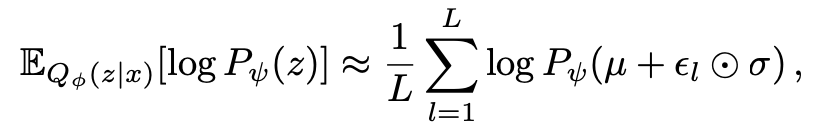

Reconstruction loss: 아니 ㅅㅂ prior 은 CNF 다시 돌려놓은거라고 치면 G-1은 뭘까;;;;