PointConv ...
- is an extension to the Monte Carlo approximation of the 3D continuous convolution operator.
- for each convolutional filter, it uses MLP to approximate a weight function
- applies a density scale to re-weight the learned weight functions.
PointConv
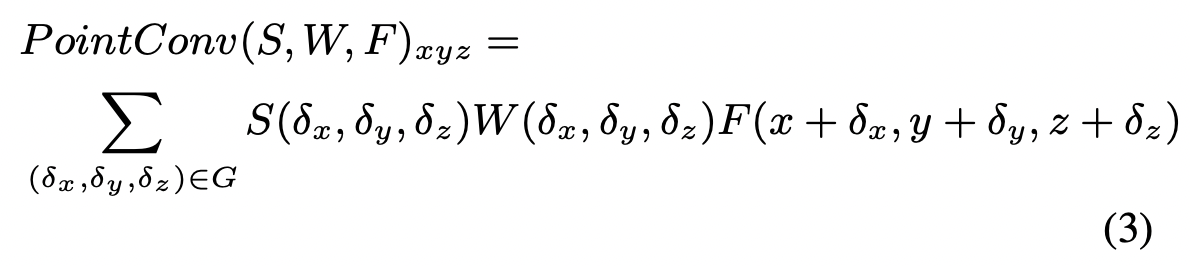
x, y, z 가 어떤 grid 의 center 이라고 생각하면, 델타값은 그 중심에서 얼마나 멀어져 있냐를 뜻함.
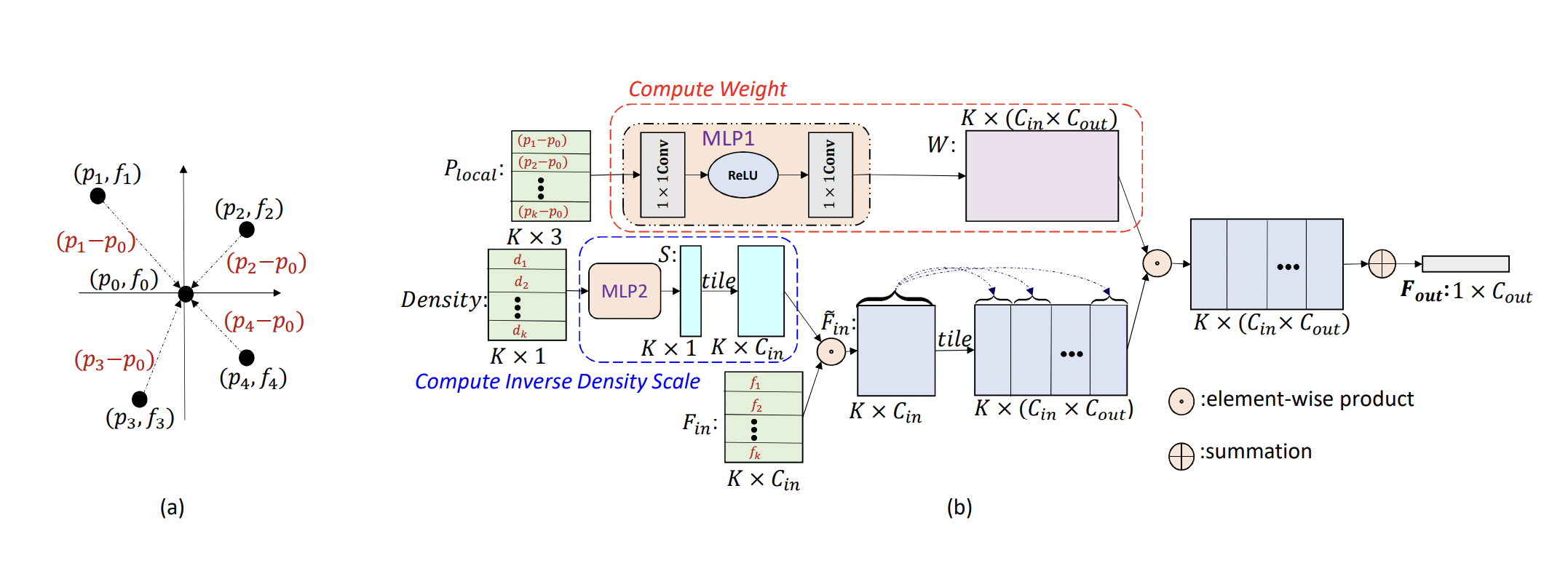
P: Local points (K x 3)
- center에서 K 개의 neareset neighbor 을 골라 상대적 거리를 구함
F: Input features (K x C_in)
- 1x1 conv 로 K x 3 -> K x C_in
W: weight function (K x C_in X C_out)
- Approximated by MLP
- Weights are shared for permutation-invariance
- 1x1 conv 로 K x C_in -> K x (C_in x C_out)
S: Inverse density (K x C_in X C_out)
- Density가 높은 지역에서의 contribution은 scale down 되어야 함
- Nonlinear transformation with MLP
즉, K 개의 distance 에서 각 점별 density 를 MLP 를 통해 구하고 (sparse 하면 높고, dense 하면 낮게), 결과물을 C_in 만큼 반복함 (numpy tile). 이를 Feature 에 곱한 뒤, 결과물을 C_out 만큼 반복함.
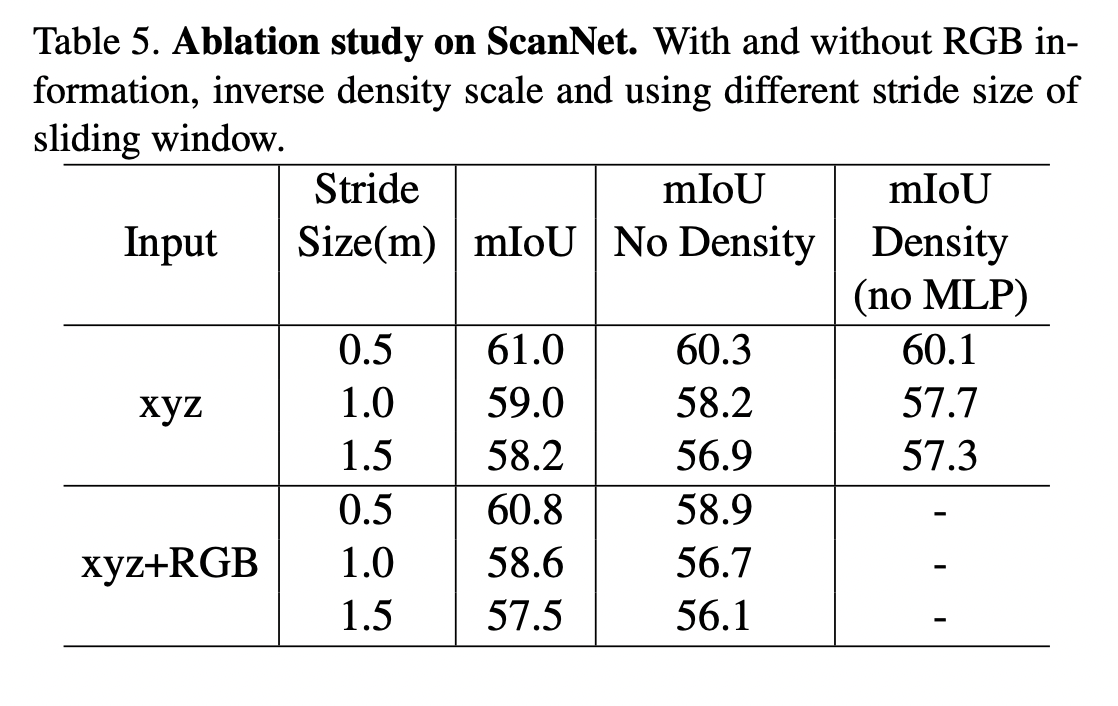
( Density scaling 을 사용한 mIoU가 높다는 결과 )
최종적으로 Element wise summation 을 통해 1 X C_out의 결과물 산출.
Efficient PointConv
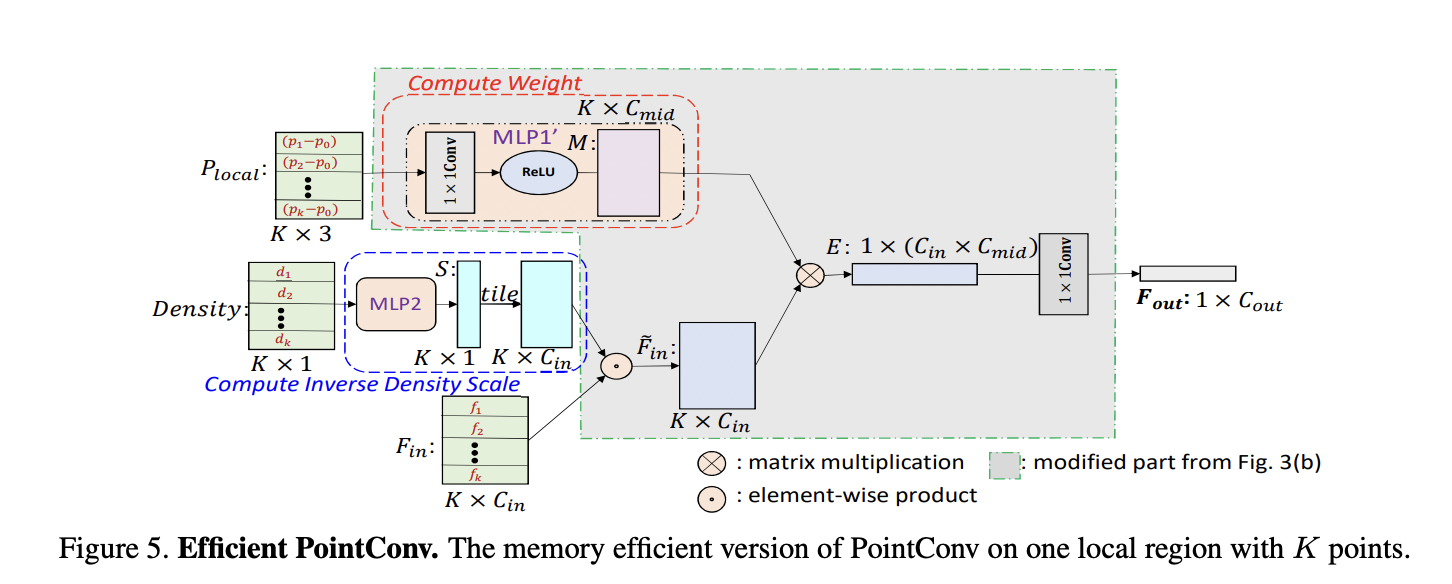
여기서 K x C_in -> K x (C_in x C_out) 을 수행하는 MLP 의 연산량이 너무 많기 때문에, matrix multiplication 과 2d conv 를 사용해 근사시키려고 한다.
실제로,
K x C_in 의 Feature 은 그대로지만, Inverse Density Scale 에서 tiling 을 하지 않고 바로 Matrix Multiplication 을 수행한다
(K x C_in)을 transpose 해서 (C_in x K) 로 바꾼 뒤
(C_in x K) x (K x C_mid) -> 1 x (C_in x C_mid)
마지막으로 결과물을 1x1 conv 로 (C_in x C_mid) -> C_out
이를 통해 K x C_in -> K x (C_in x C_out) 를 할 걸 K x C_in -> K x C_mid 로 줄이게 되는데, 이가
C_mid / (K x C_out) ~= 1/64 의 메모리 절감 효과를 보인다고 한다.
