Motivation
Previous approaches have assumed the importance of elaborate local extractor for point cloud analysis.
However, this is mistaken!
- Extractors are prohibitively computation-heavy
- Extractors already capture geometric properties well
-> why do we need local extractors in the first place?
Key idea
Build a deep network ONLY with residual feed-forward MLPs
Related Work
Point cloud analysis
By conversion
We can convert the data into voxels, but this may result in information loss
By directly using pointcloud
PointNet++
Local Geometry Exploration
- Convolution (Pointconv)
- Graph-Based
- Attention-Based (Point Transformer)
Deep Residual MLP
Pointnet Revisited
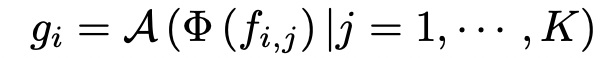
각 instance i 마다 K 개의 이웃 점이 있었다는 것을 상기하자. 그렇다면 그 instance 의 local feature 은 Φ (MLP) 이후 aggregate function (max-pooling) 으로 얻어졌었다.
최근 paper 에서는 이 Φ 를 더 고도화된 함수로 바꾸는 것에 집중했는데, 대표적으로 RSCNN과 Point Transformer 이 있다.
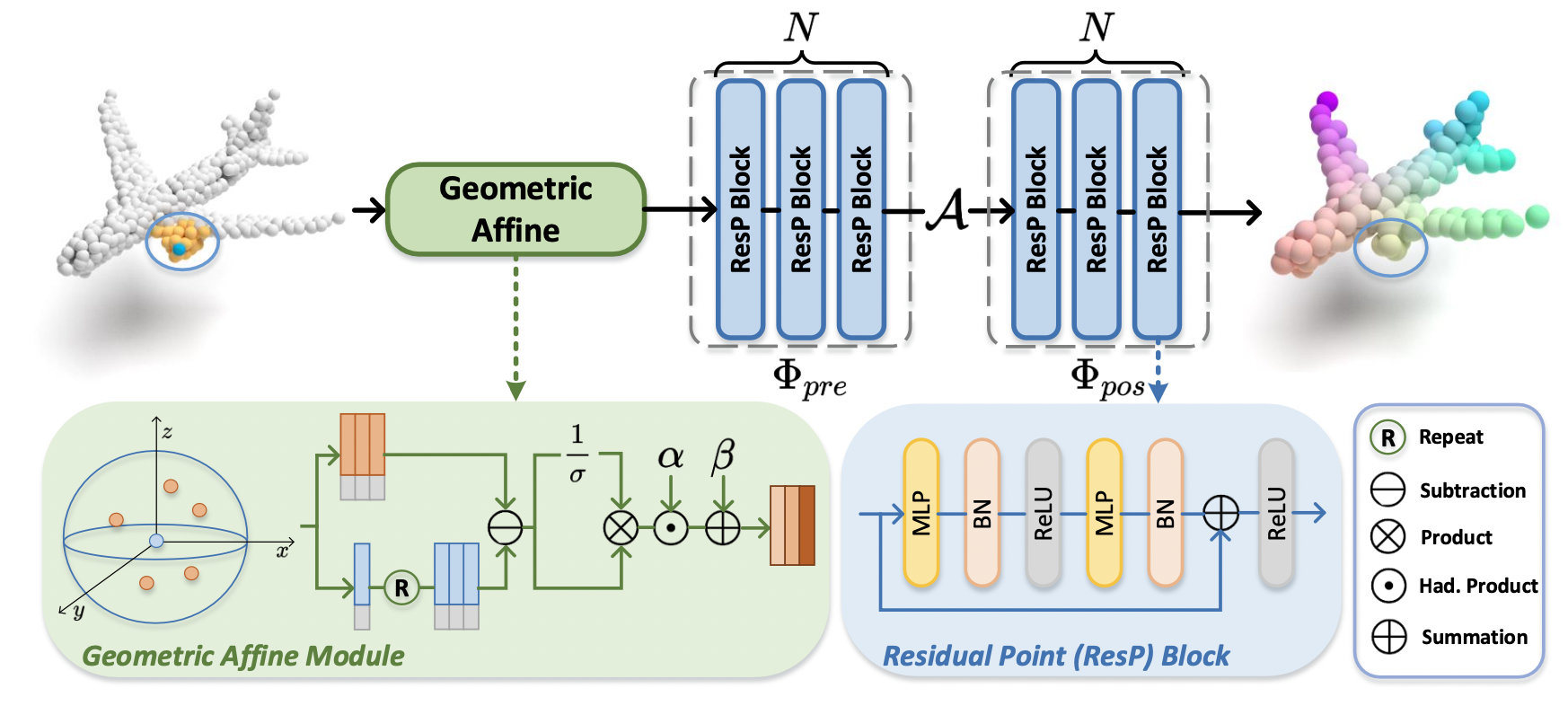
Figure 2. PointMLP 의 단층
PointMLP Framework
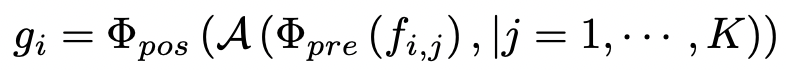
Φpos 가 추가되었다! 이는 max-pooling 을 진행한 뒤 MLP를 한번 더 (!!) 돌리겠다는 뜻이다.
각 ResP 블록에서는 MLP(x) + x (residual connection) 이 수행된다.
즉, 정리하자면,
Φpre: shared weights (어떤 점에 가중치를 두어야 하는가?)
A: 각 instance 에 대해 가장 중요한 점 추출
Φpos: 그 점을 토대로 deep aggregate feature 추출
이며, 이는
- MLP 를 사용하기 때문에 permutation-invariance 가 유지됨
- ResNet 마냥 부담없이 깊게 쌓을 수 있음
- 층을 깊게 쌓아도 효율적임
단, 저자들은 깊이에 성능이 크게 좌우되지 않음을 강조한다. ablation study 를 진행했을 때 40층이 최적이라고도 기록했다.
Geometric Affine Module
단, 무지성으로 MLP Block 을 쌓는 행위는 정확성의 감소로 이어지는데, 저자들은 이가 다양한 기하학적 orientation 때문으로 보고 이를 교정할 수 있는 module 을 제안함.
과연 다른 paper은 이 생각을 안했을까? 다른 모델에 해당 모듈을 실험해 보았을 때, 모델마다 편차가 존재했음.
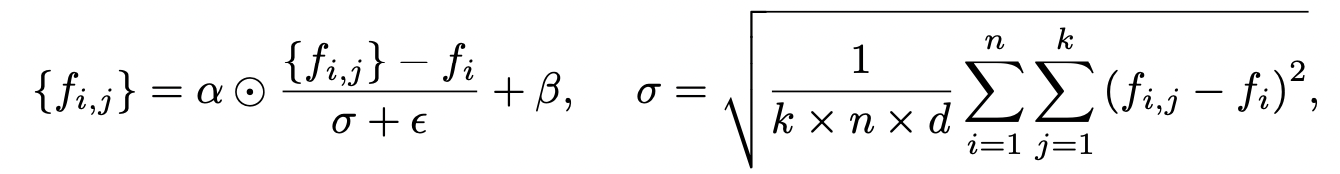
사실 그냥 normalization 후 각 neighbor 에 대해서 가중치를 곱해주는 것이다.
# Group points
idx = knn_point(self.kneighbors, xyz, new_xyz)
grouped_xyz = index_points(xyz, idx) # [B, npoint, k, 3]
grouped_points = index_points(points, idx) # [B, npoint, k, d]
# Calculate fi and sigma
mean = torch.mean(grouped_points, dim=2, keepdim=True)
std = torch.std((grouped_points - mean).reshape(B, -1), dim=-1, keepdim=True).unsqueeze(dim=-1).unsqueeze(dim=-1)
# Perform Normalization
grouped_points = (grouped_points - mean) / (std + 1e-5)
grouped_points = self.affine_alpha * grouped_points + self.affine_beta이 때 sigma 의 계산은, 중심점에 대해 분산을 구한 뒤, k (neighbor 의 수), n (point 의 수), d (차원의 수, 3) 를 곱한만큼 눈 뒤에 제곱근을 씌운다.
이 때 normalization 보다 중요한 것은, alpha 와 beta 를 학습 가능하게 만들어 모델이 최적의 affine을 찾도록 하는 것이다.
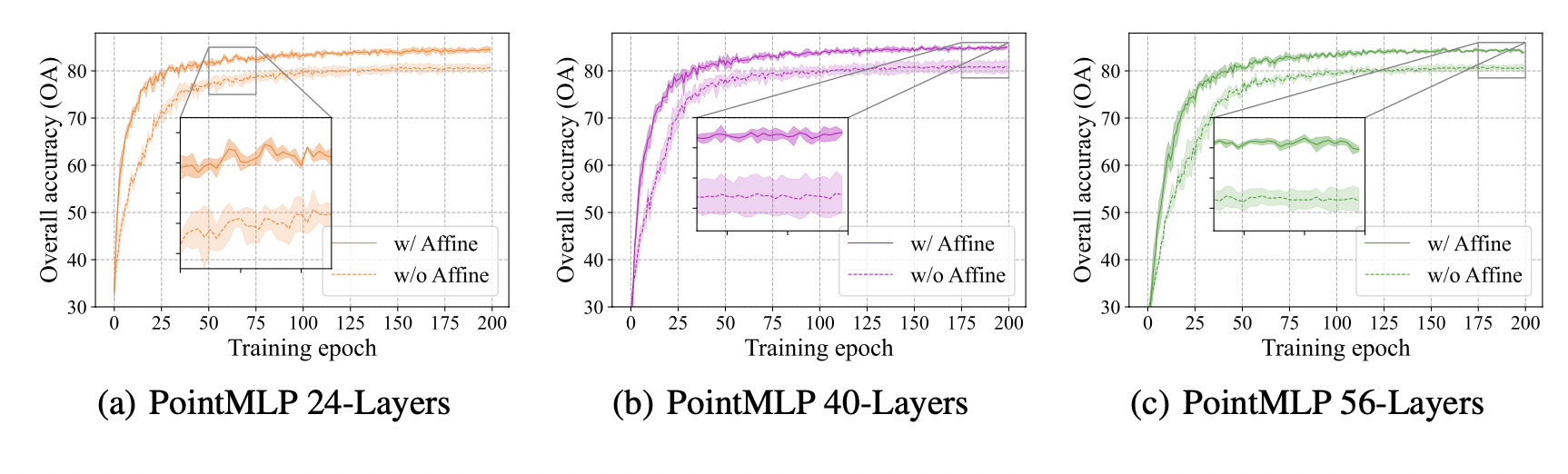
해당 모듈의 도입 덕에 일관적인 성능 향상을 한 것이 보인다.
