Priority Queue를 Heap으로 구현하기 위해 필요한 개념 및 구현 방식을 살펴보고, JavaScript로 구현해보는 글입니다.
☪️ Priority Queue
*️⃣ 정의
- 일반 큐와 다르게 요소들이 우선순위를 가져, 우선순위 순서대로 out 되는 큐.
- min priority queue, max priority queue가 있음.
*️⃣ 기능
- empty: 비어있는지 여부를 알려줌.
- size: 요소들의 개수를 알려줌.
- insert(push): 요소를 추가함.
- top: min/max 값을 가져옴.
- remove(pop): min/max 값을 삭제함.
*️⃣ 시간 복잡도
heap을 사용하여 구현한다고 가정.
- empty, size, top => O(1)
- insert, remove => O(log n)
*️⃣ 활용
1. 정렬
요소 자체를 priority로 하여 priority queue에 삽입하면 됨.
- min priority queue - 오름차순 정렬
- max priority queue - 내림차순 정렬
2. 머신 스케줄링
OS, 공장 같은 곳에서의 스케줄링에 활용 가능.
현재 작업 진행도를 key(priority)로 가진 머신을 min priority queue에 넣으면 태스크를 효율적으로 할당시킬 수 있다.
(끝나는 시간이 가장 빠른 머신에게 새로운 태스크를 줌.)
🔯 Min/Max Tree
heap을 알기 위해서는 먼저 min/max tree를 알아야 한다.
*️⃣ 정의
어떤 subtree를 보아도 root가 min/max 값인 트리.
즉, 부모 노드는 무조건 자식보다 작거나(min) 크며(max), 같을 수 있다.
*️⃣ 예시
-
min tree
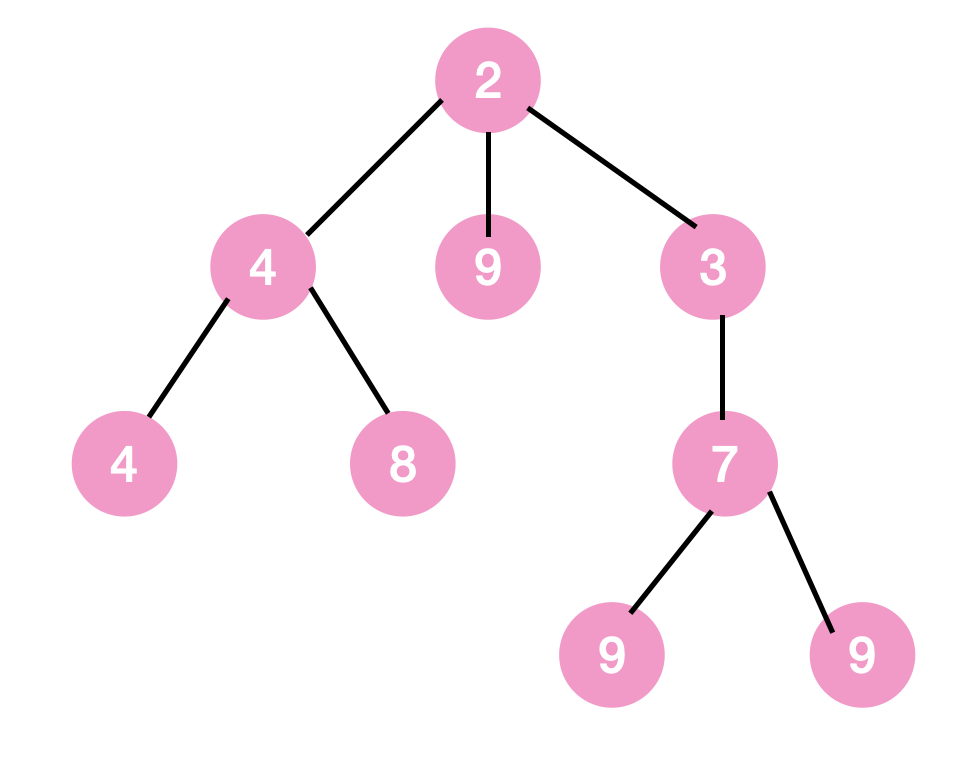
-
max tree
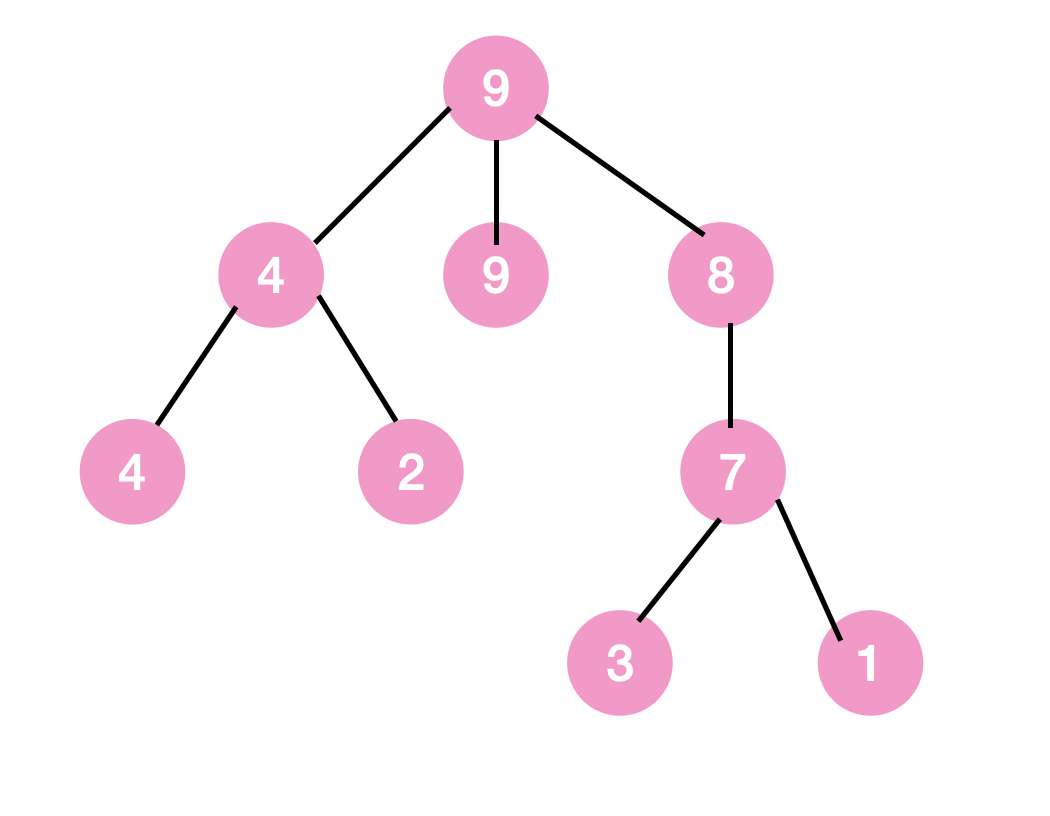
♒️ Heap
priority queue는 heap을 이용하여 효과적으로 구현할 수 있다.
참고로 priority queue와 heap은 리스트-연결 리스트 또는 리스트-배열 관계와 같다고 보면 된다.
*️⃣ 정의
- priority queue와 마찬가지로 min heap, max heap이 있음.
- complete binary tree이면서, min/max tree임.
*️⃣ 예시
n = 9인 min heap 만들어보기
-
n = 9인 complete binary tree 만들기
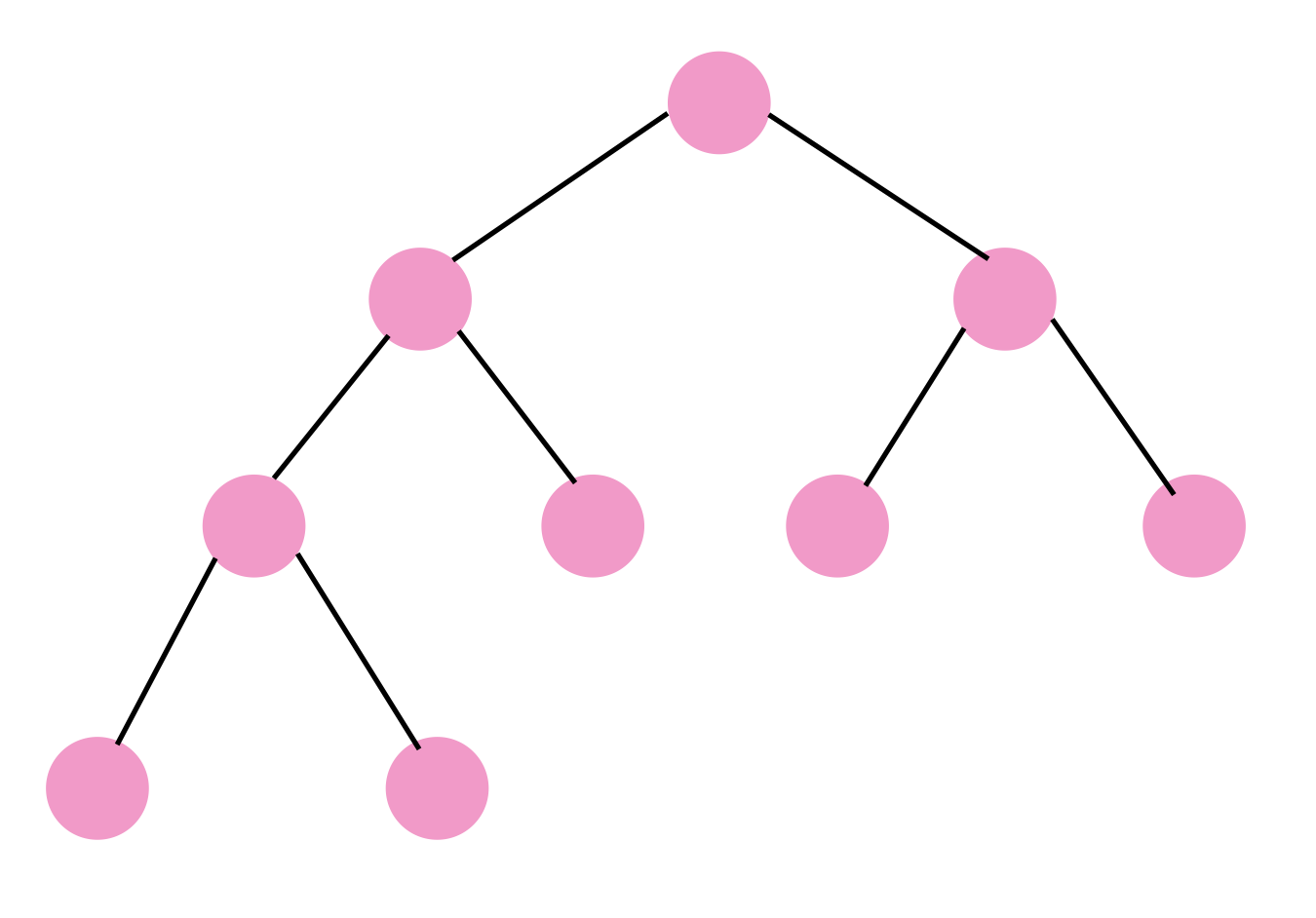
-
min tree로 만들기 === 완성
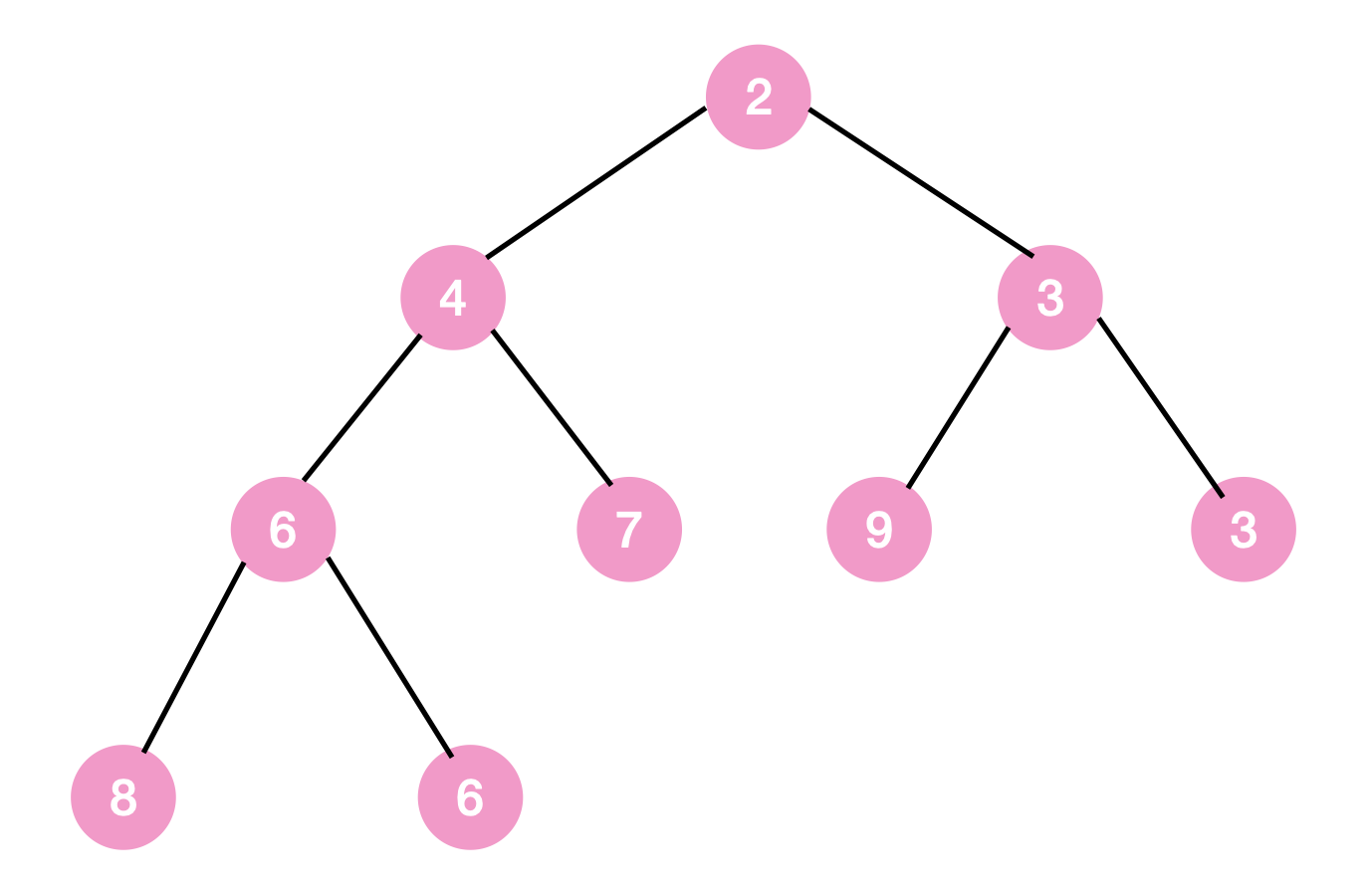
*️⃣ Height
complete binary tree이기 때문에 log2(n+1).
⚛️ Heap 구현하기
구현 방식 및 시간 복잡도에 대해 먼저 설명합니다. 전체 코드는 마지막에 있습니다.
*️⃣ 표현 방법
heap은 일반적으로 배열을 사용하여 표현한다.
binary tree를 표현하는 방법은 2가지가 있다.
- 배열
- 연결 리스트
binary tree를 배열로 표현하게 되면 오른쪽으로 치우쳐진 트리, 즉 왼쪽 노드가 많이 없는 경우에는 메모리를 쓸데 없이 낭비하게 된다.
하지만 heap은 complete binary tree이기 때문에 그러한 문제가 없다.
또한 배열 index를 통해 부모 및 자식 노드를 쉽게 찾을 수 있기 때문에 효과적이다.
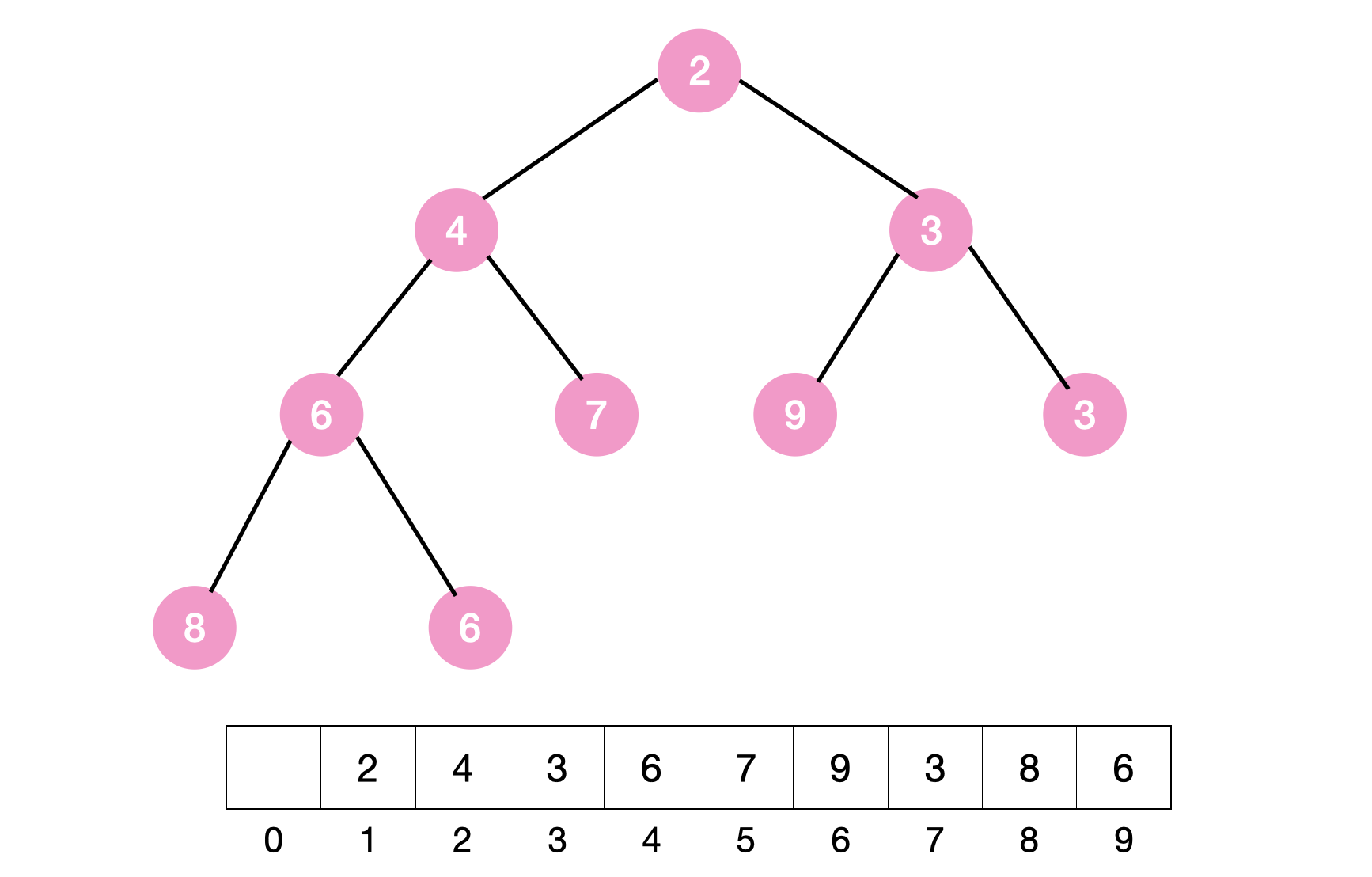
*️⃣ 부모-자식 노드 간 이동
operation들을 실행하며 부모-자식 노드 간 이동이 일어난다.
이동할 부모 or 자식 노드의 위치는 배열의 index 계산을 통해 알아낼 수 있다.
부모 -> 자식
- left child: 2 * i
- right child: 2 * i + 1
자식 -> 부모
i / 2
*️⃣ Insert(Push)
아래 max heap에 20을 추가하는 과정을 통해 설명해보겠다.
* min heap은 대소 관계만 반대로 적용하면 된다.
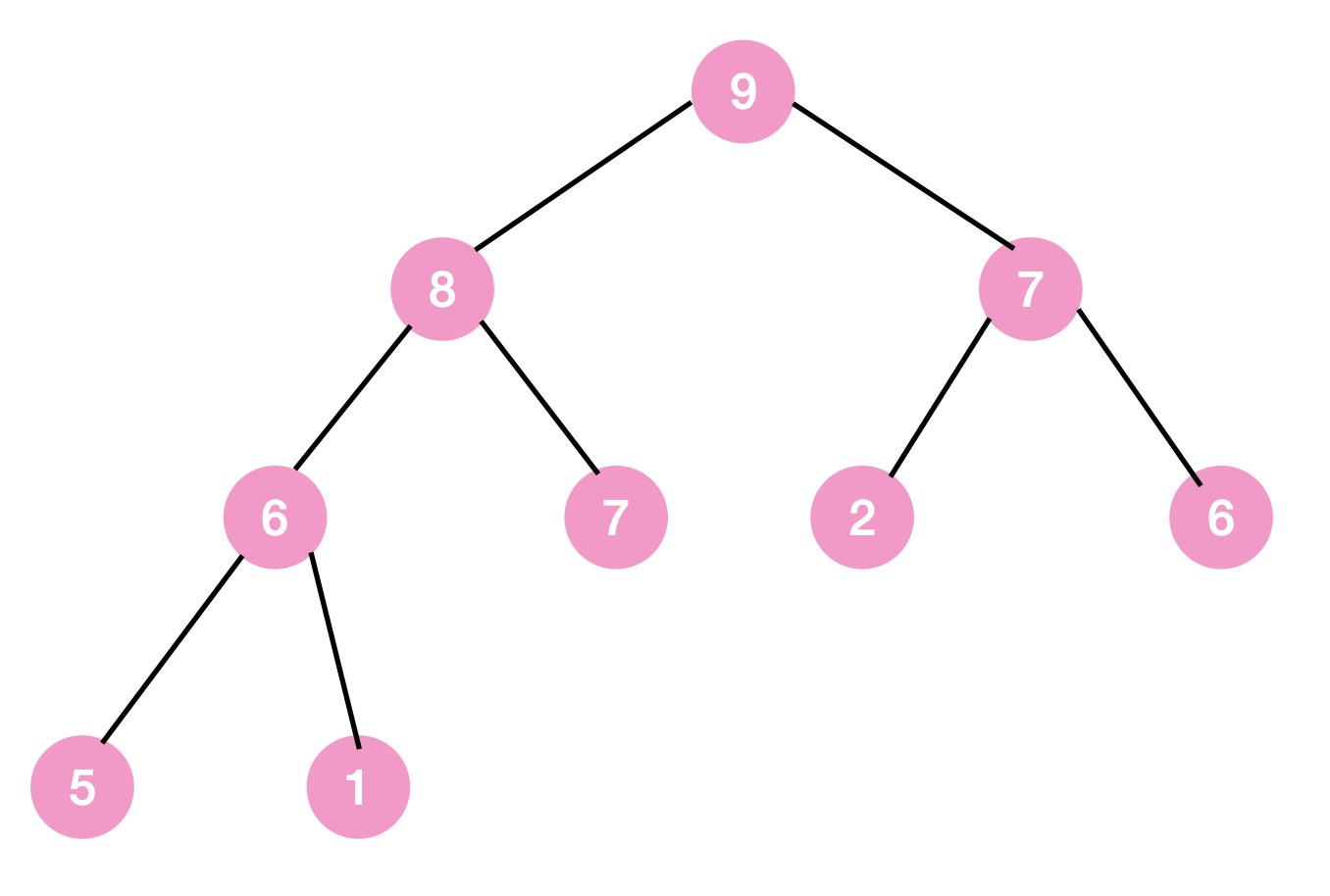
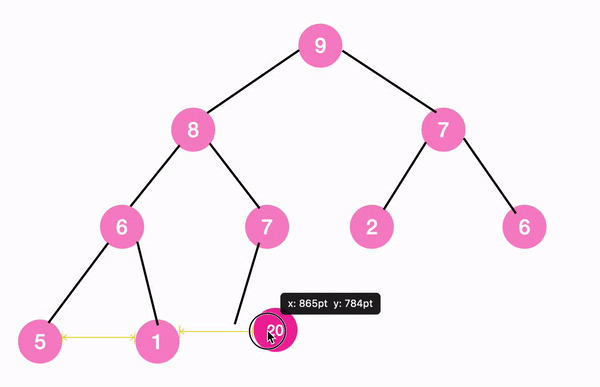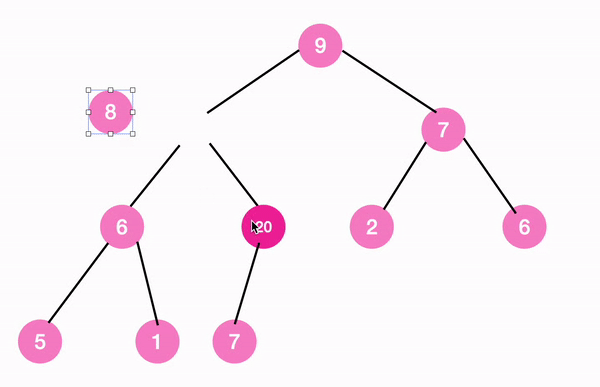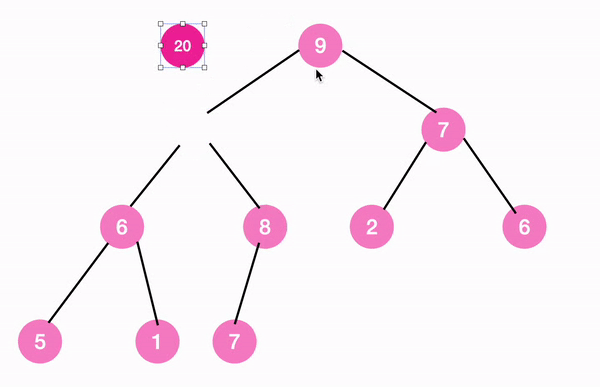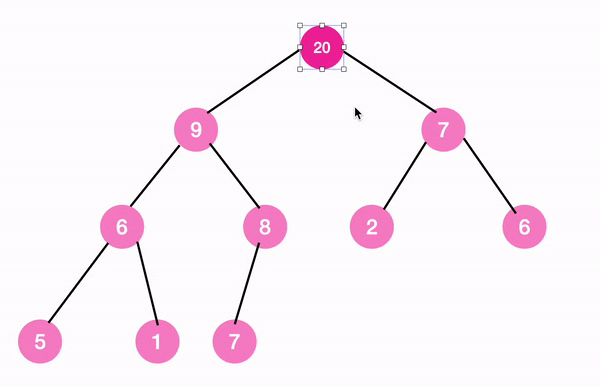
1단계
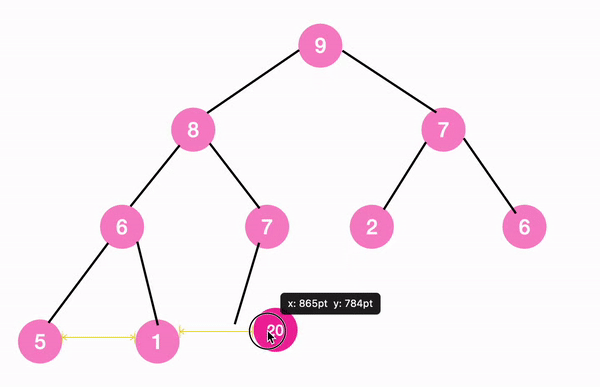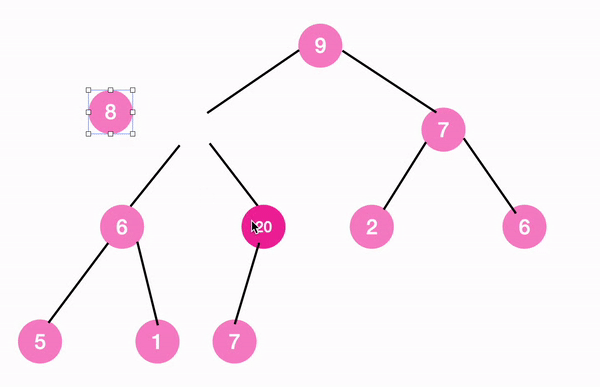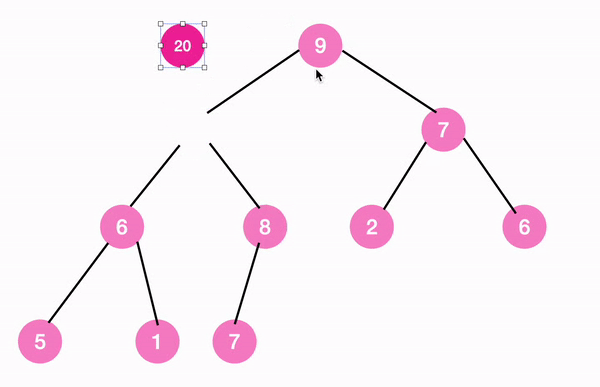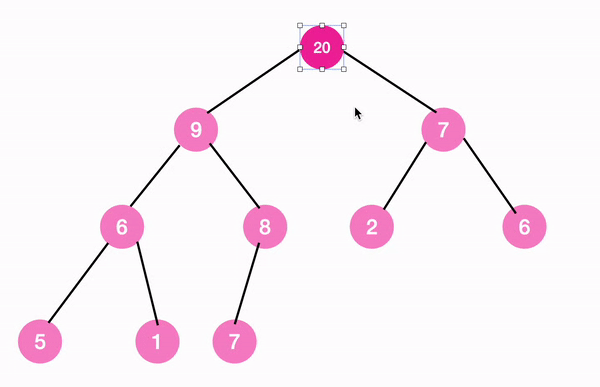
complete binary tree의 형태에 맞추어 일단 마지막 노드 바로 뒤에 20을 추가한다.
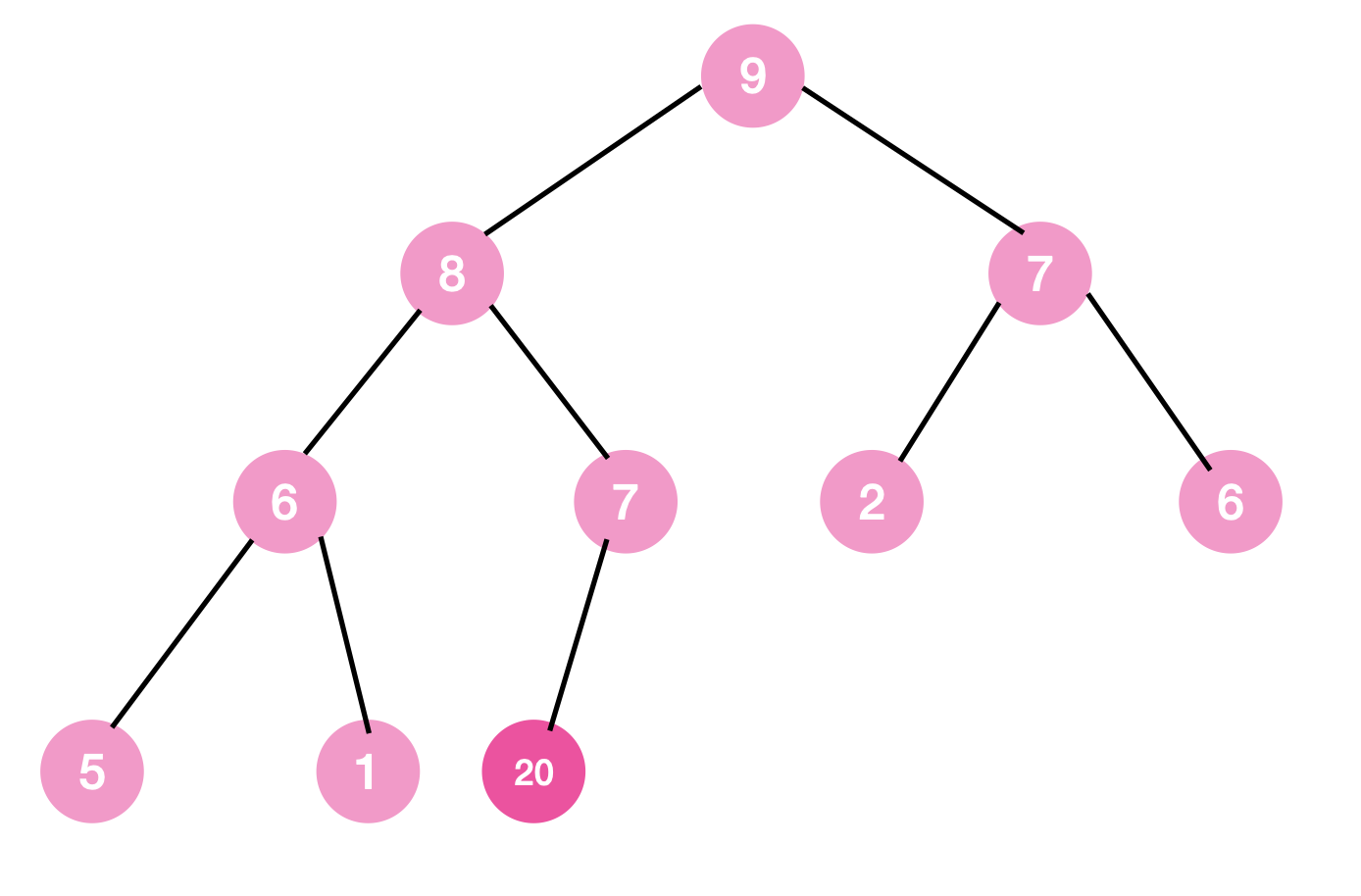
2단계
1단계를 마친, 현재 상태가 max tree에 조건에 부합하는지 확인해야 한다.
max tree의 정의에 따르면 새로 추가한 노드가 영향을 미치는 범위는 아래 노란색으로 표시한 경로다.
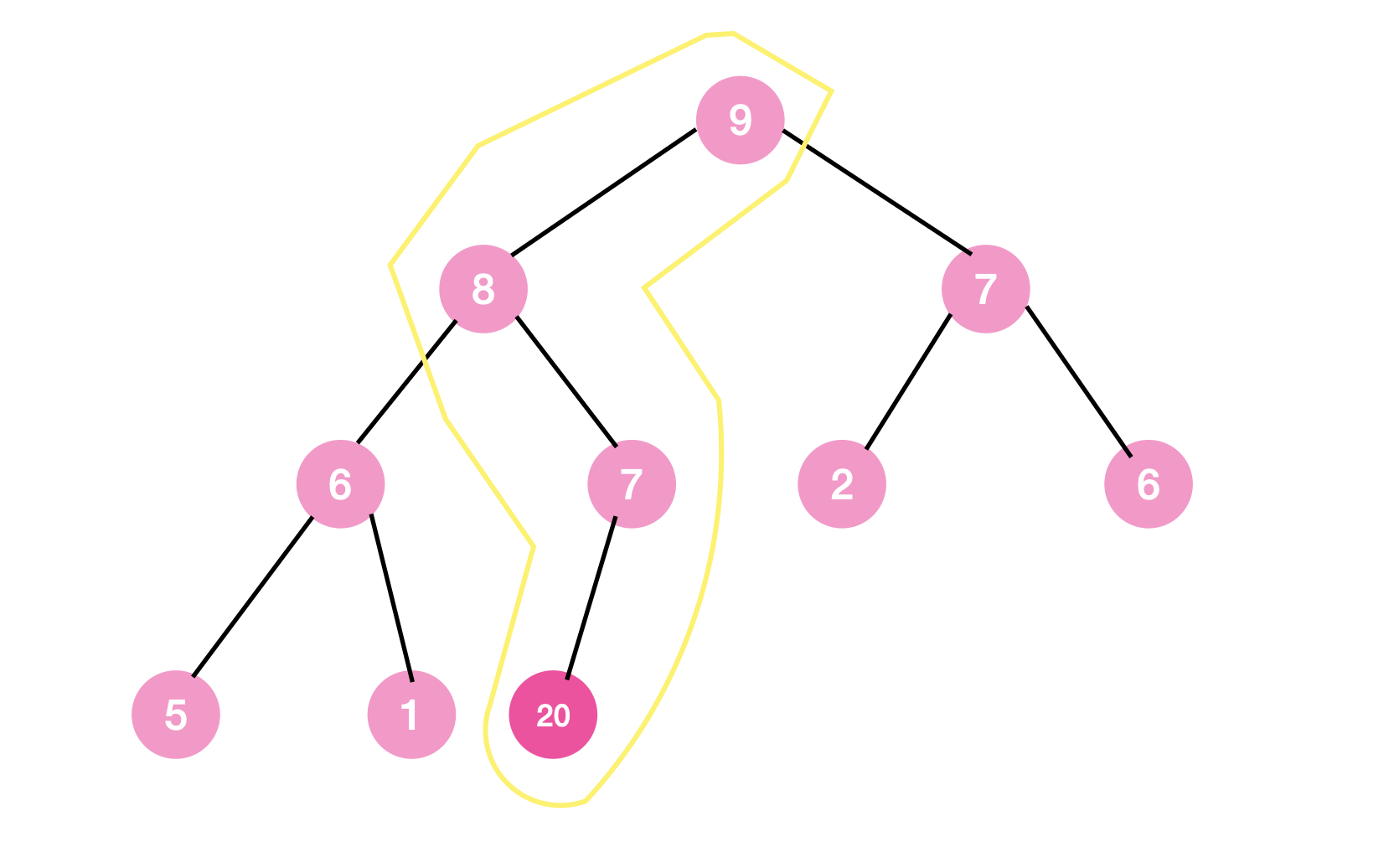
이 경로만 확인해보면 된다.
즉, 현재 위치에서부터 root 노드까지 max tree 조건에 부합할 때까지, 계속해서 부모 노드와 비교하여 조건에 부합하지 않는다면 자리를 바꾸어 나가면 되는 것이다.
최종 결과
따라서 아래 모습을 갖추게 된다.
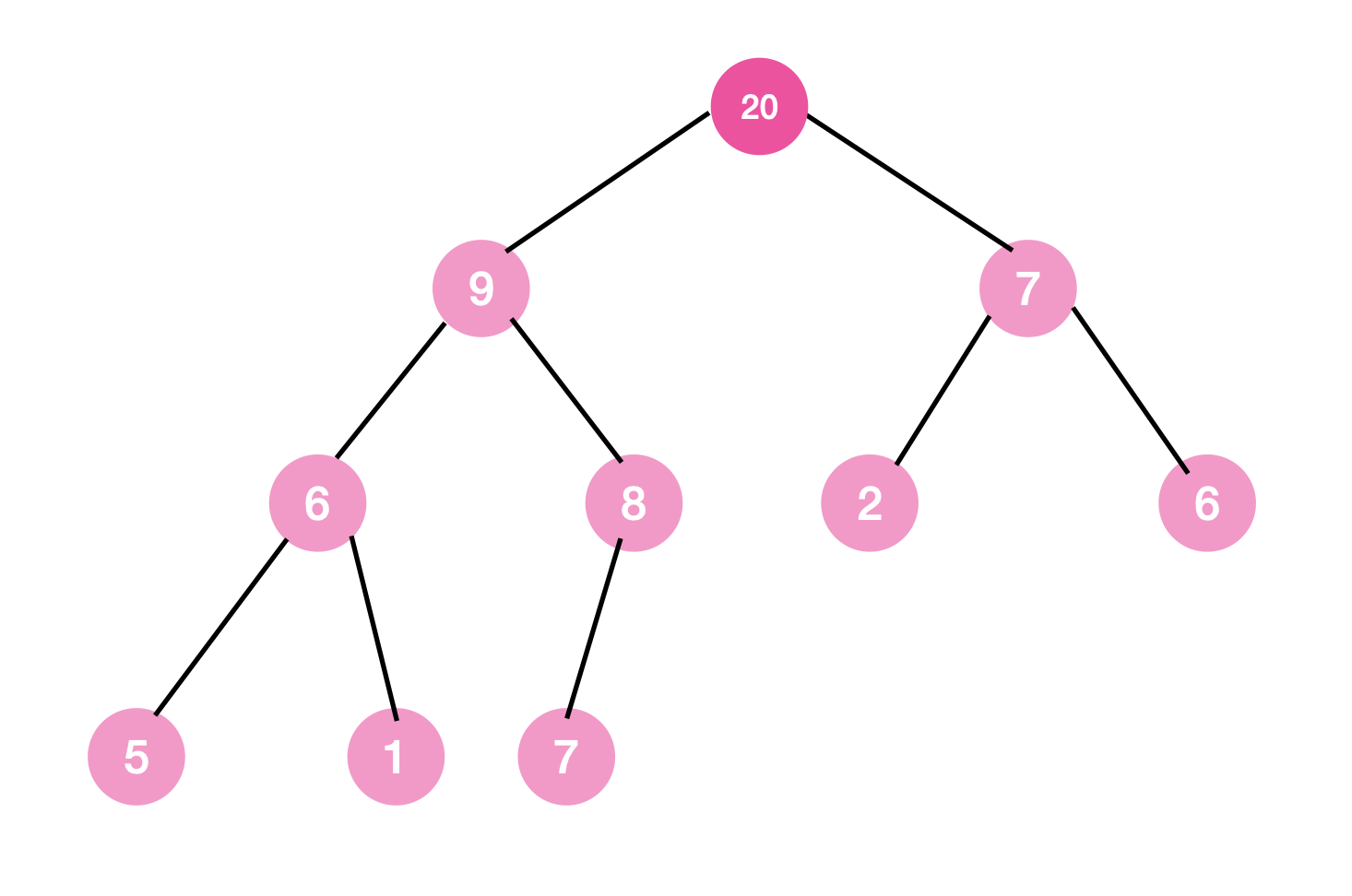
시간 복잡도
최악의 경우 마지막 레벨을 제외한 모든 레벨의 부모 노드와 비교 후 교체를 해주어야 한다.
이는 결국 레벨의 개수 즉, 트리의 높이가 곧 시간 복잡도라는 것을 알 수 있다.
위에서 언급했듯이 heap은 complete binary tree이기 때문에 높이가 log2(n+1)이다.
따라서 insert의 시간 복잡도는 O(log n)이다.
*️⃣ Remove(Pop)
아래 max heap에서 remove하는 과정을 통해 설명해보겠다.
* min heap은 대소 관계만 반대로 적용하면 된다.
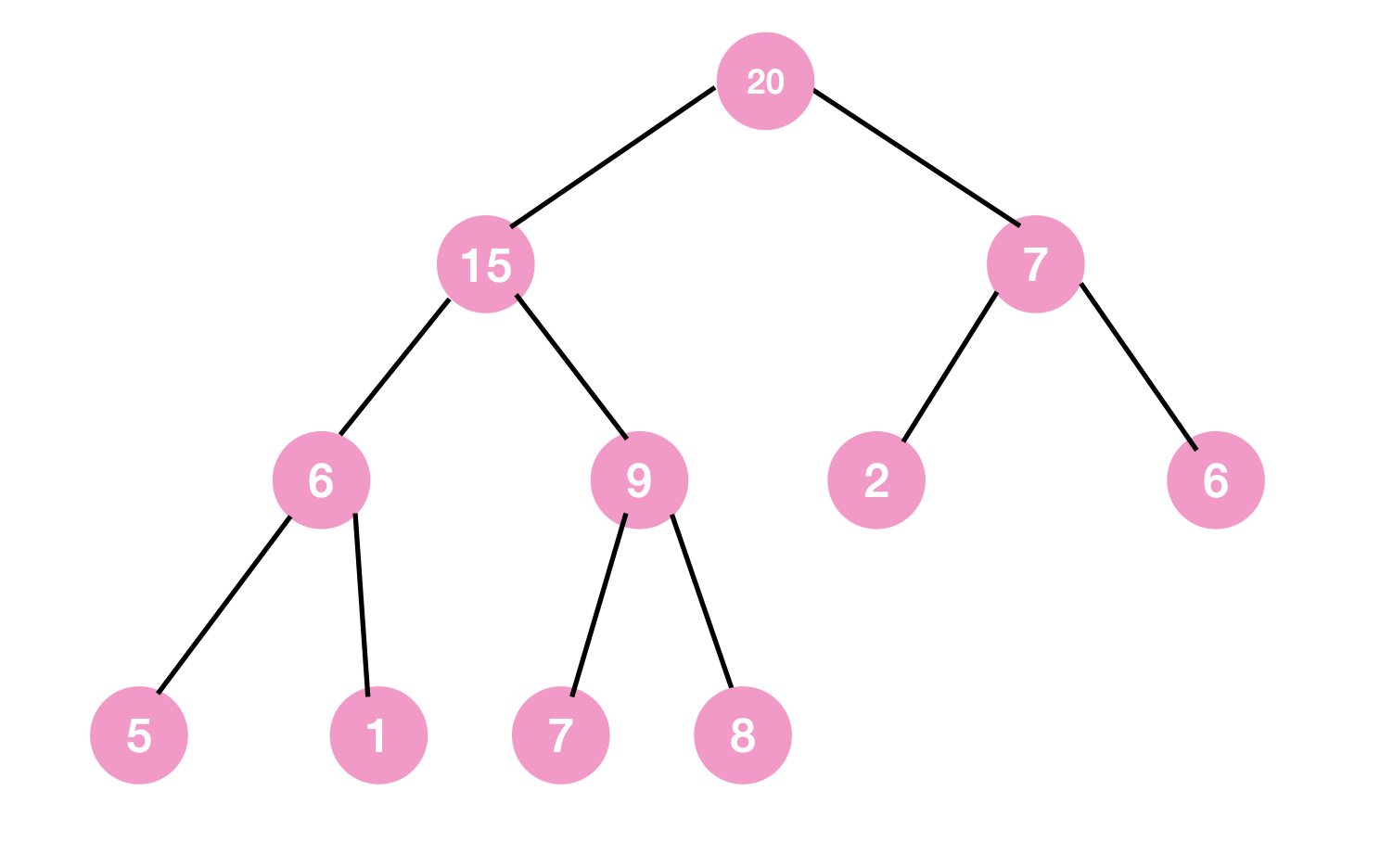
1단계
위 heap에서 원소 하나가 줄면 무조건 아래와 같은 형태가 되어야 한다. (complete binary tree이기 때문에)

그런데 heap은 top 즉, root 노드를 삭제해야 한다.

따라서 실제로 삭제되어야 할 root 노드를 삭제하고, 구조상 없어져야 하는 마지막 노드를 root 자리로 옮긴다.
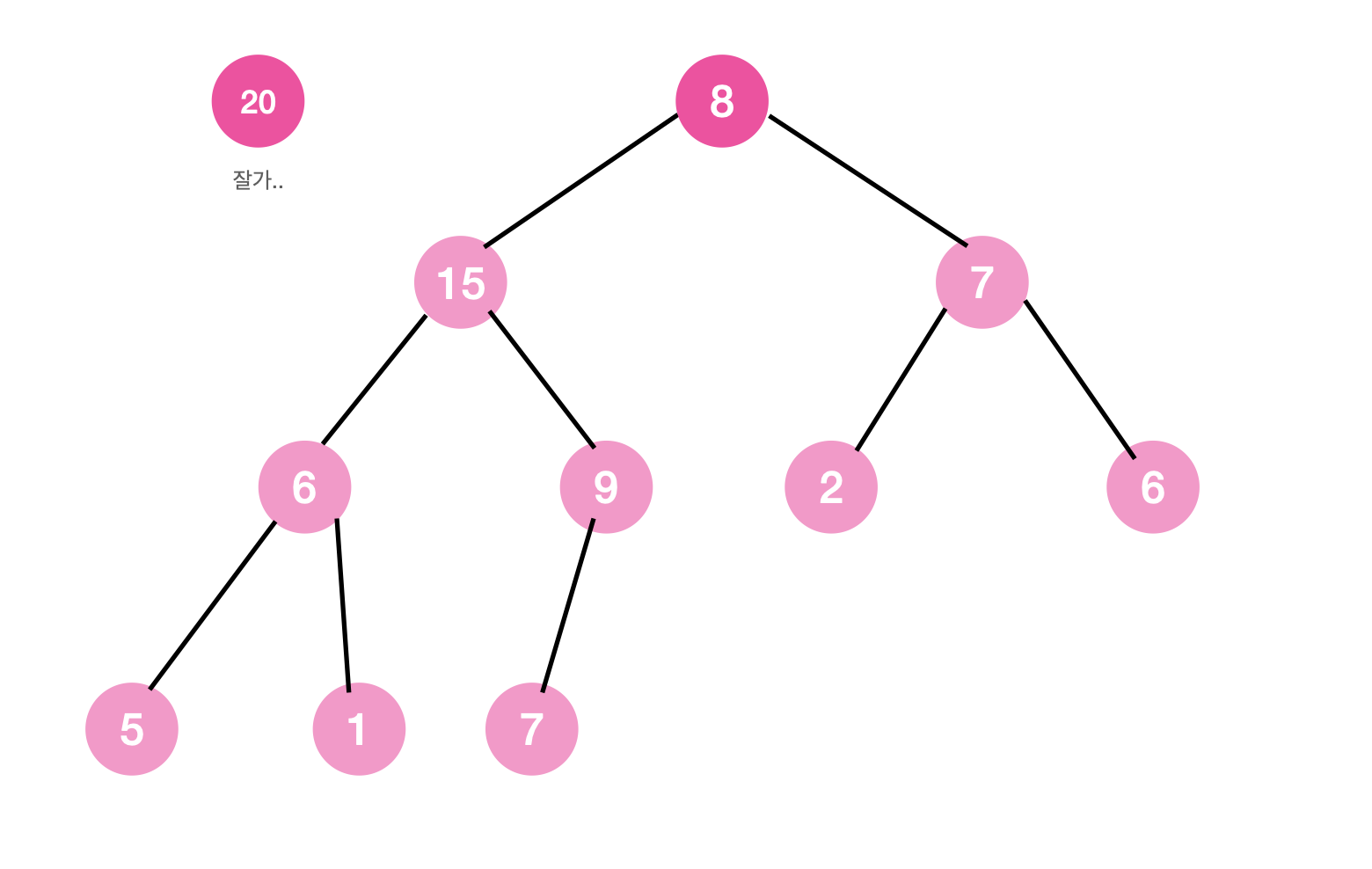
2단계
마지막 노드를 root로 옮겼으니 max tree의 조건에 부합하지 않을 가능성이 매우 크다.
(자식 노드가 부모 노드와 같을 수 있으니 무조건적으로 max tree의 형태가 깨지는 것은 아님.)
따라서 다시 max tree의 형태를 갖추도록 하는 작업이 필요하다.
그 방법은 다음과 같다.
(1) root 노드의 자식 노드 중 큰 것을 선택한다.
(2) 선택된 자식 노드와 root 노드를 비교한다.
* 자식 노드가 하나라면 그 자식 노드 하나와 비교.
(3-1) root 노드가 더 작다면 자리를 바꾼다.
(3-2) root 노드가 더 크다면 max tree의 형태를 갖춘 것이니 작업을 끝낸다.
(4) 위 작업이 (3-1)에서 끝났다면, root 노드를 옮겨진 노드로 대체하여, (3-2)에서 끝나거나 자식 노드가 없을 때까지 작업을 반복한다.

- 자식 노드 15, 7 중 더 큰 15와 비교했더니 더 작아서 교체
- 자식 노드 6, 9 중 더 큰 9와 비교했더니 더 작아서 교체
- 자식 노드 7과 비교했더니 더 커서 작업 완료
최종적으로 다음과 같이 max tree의 형태를 갖추어, remove 작업을 완료하게 된다.
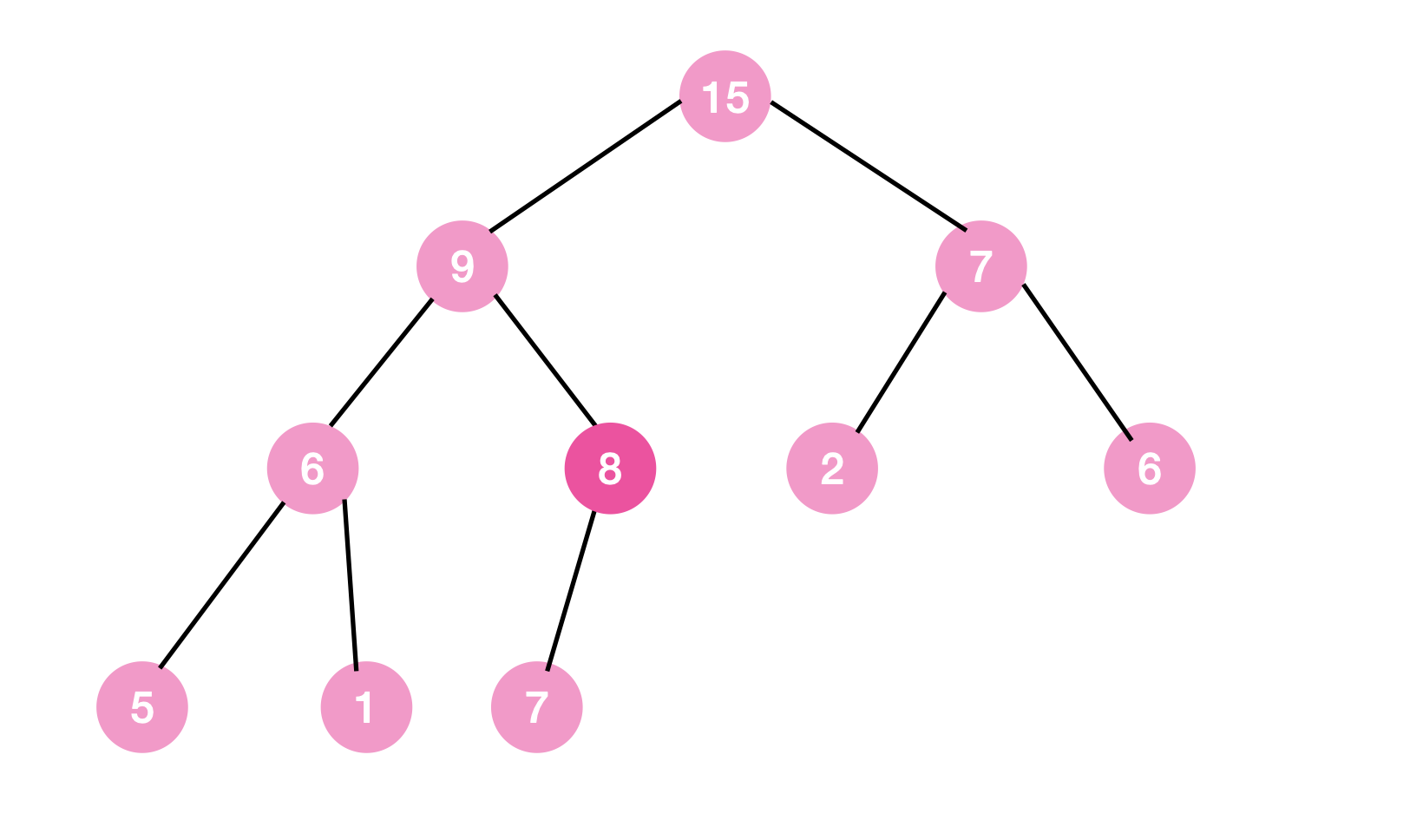
시간 복잡도
remove 또한 insert와 마찬가지로 최악의 경우 트리의 높이만큼 작업을 수행해야 한다.
따라서 O(log n)이다.
*️⃣ Top
root 노드 조회 === 배열의 1번째 원소 get
시간 복잡도
O(1)
*️⃣ Size, Empty
배열의 길이 확인 (Array.length - 1)
시간 복잡도
O(1)
*️⃣ JavaScript 코드
MinHeap
class MinHeap {
constructor() {
this.heap = [null];
}
getMin() {
return this.heap[1];
}
getSize() {
return this.heap.length - 1;
}
isEmpty() {
return this.heap.length < 2;
}
insert(node) {
let current = this.heap.length;
while (current > 1) {
const parent = Math.floor(current / 2);
if (this.heap[parent] > node) {
this.heap[current] = this.heap[parent];
current = parent;
} else break;
}
this.heap[current] = node;
}
remove() {
let min = this.heap[1];
if (this.heap.length > 2) {
this.heap[1] = this.heap[this.heap.length - 1];
this.heap.splice(this.heap.length - 1);
let current = 1;
let leftChildIndex = current * 2;
let rightChildIndex = current * 2 + 1;
while (this.heap[leftChildIndex]) {
let childIndexToCompare = leftChildIndex;
if (
this.heap[rightChildIndex] &&
this.heap[rightChildIndex] < this.heap[childIndexToCompare]
)
childIndexToCompare = rightChildIndex;
if (this.heap[current] > this.heap[childIndexToCompare]) {
[this.heap[current], this.heap[childIndexToCompare]] = [
this.heap[childIndexToCompare],
this.heap[current],
];
current = childIndexToCompare;
} else break;
leftChildIndex = current * 2;
rightChildIndex = current * 2 + 1;
}
} else if (this.heap.length === 2) {
this.heap.splice(1, 1);
} else {
return null;
}
return min;
}
}
MaxHeap
class MaxHeap {
constructor() {
this.heap = [null];
}
getMax() {
return this.heap[1];
}
getSize() {
return this.heap.length - 1;
}
isEmpty() {
return this.heap.length < 2;
}
insert(node) {
let current = this.heap.length;
while (current > 1) {
const parent = Math.floor(current / 2);
if (this.heap[parent] < node) {
this.heap[current] = this.heap[parent];
current = parent;
} else break;
}
this.heap[current] = node;
}
remove() {
let max = this.heap[1];
if (this.heap.length > 2) {
this.heap[1] = this.heap[this.heap.length - 1];
this.heap.splice(this.heap.length - 1);
let current = 1;
let leftChildIndex = current * 2;
let rightChildIndex = current * 2 + 1;
while (this.heap[leftChildIndex]) {
let childIndexToCompare = leftChildIndex;
if (
this.heap[rightChildIndex] &&
this.heap[rightChildIndex] > this.heap[childIndexToCompare]
)
childIndexToCompare = rightChildIndex;
if (this.heap[current] < this.heap[childIndexToCompare]) {
[this.heap[current], this.heap[childIndexToCompare]] = [
this.heap[childIndexToCompare],
this.heap[current],
];
current = childIndexToCompare;
} else break;
leftChildIndex = current * 2;
rightChildIndex = current * 2 + 1;
}
} else if (this.heap.length === 2) {
this.heap.splice(1, 1);
} else {
return null;
}
return max;
}
}
