1. 문제 소개

요약
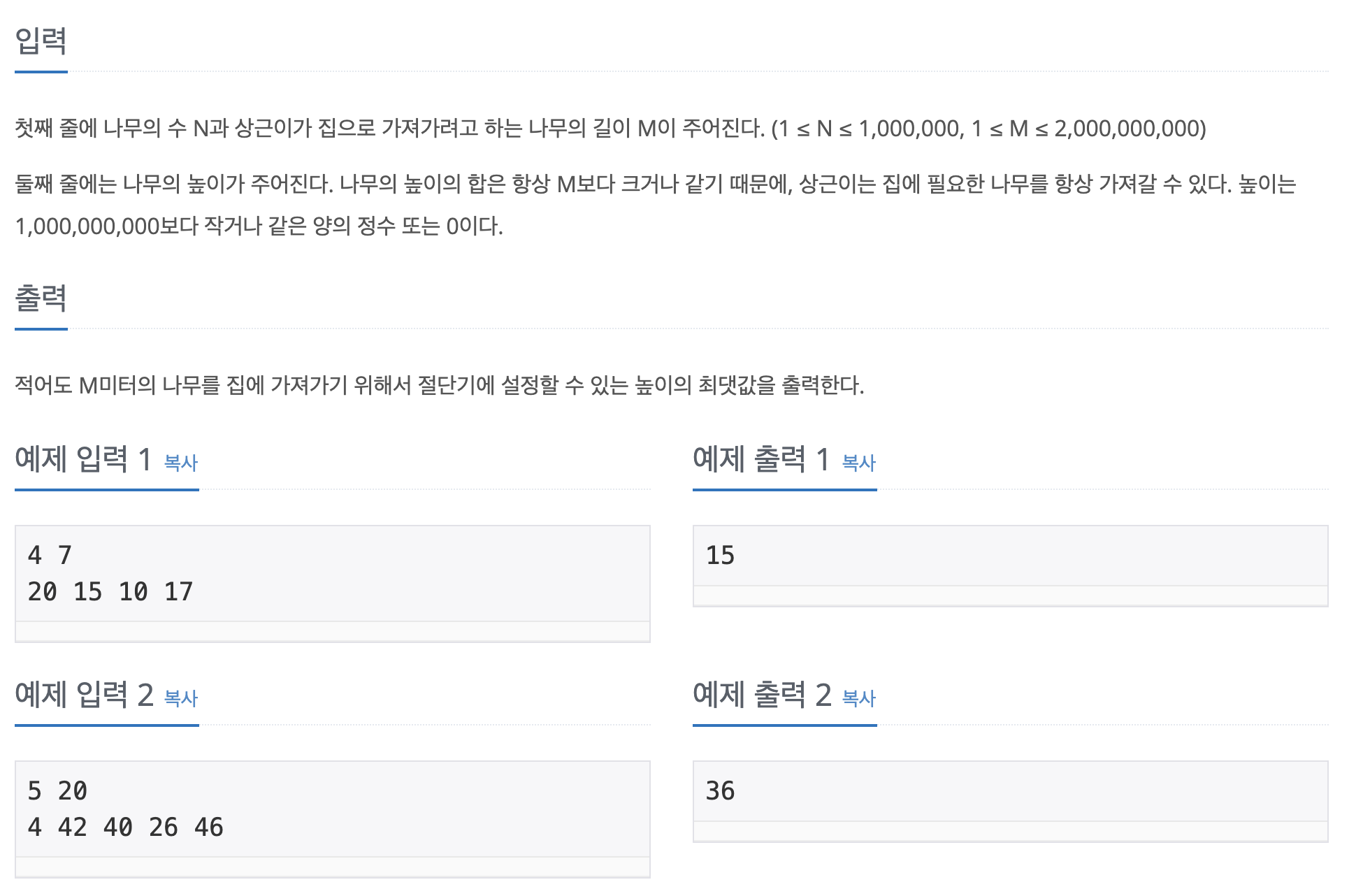
M미터의 나무가 필요해서 나무를 베려고 한다.
나무 절단기는 H 높이 만큼의 나무를 자를 수 있으며, 나무들의 높이가 주어진다.
H를 어떻게 설정해야 M미터를 채우면서 최소한으로 나무를 자를 수 있을까?
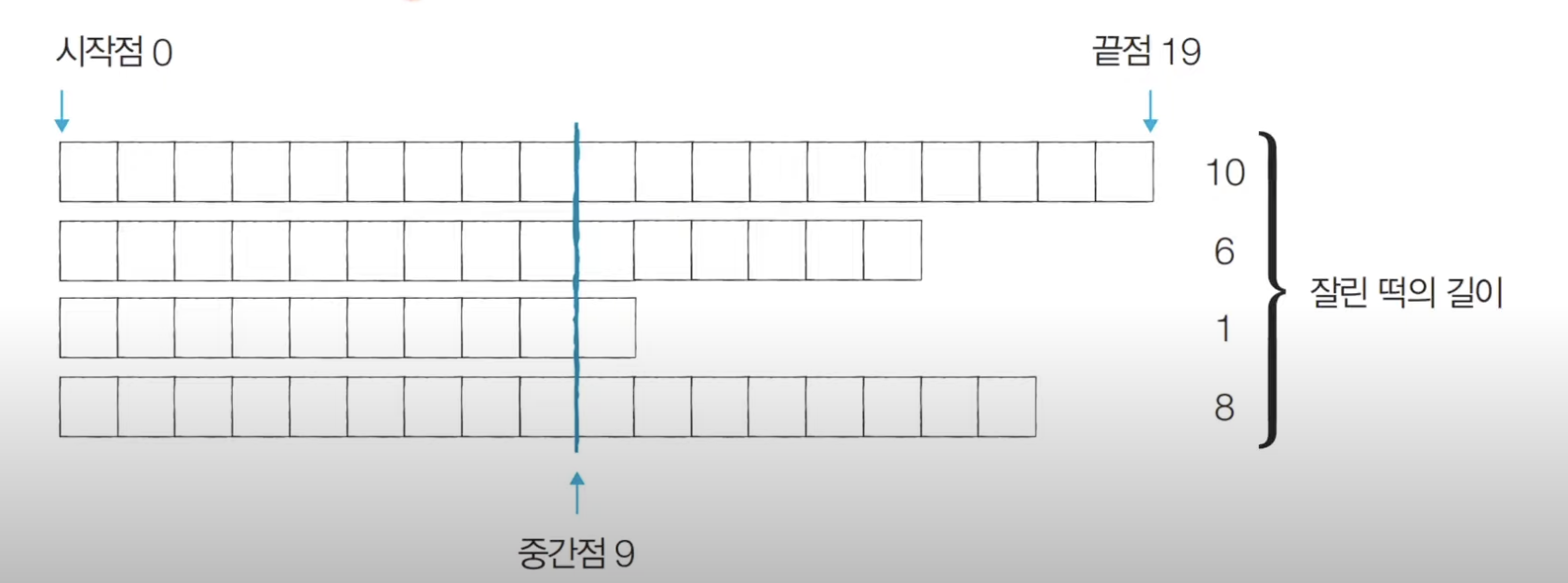
문제 이해를 돕기 위한 이미지
출처 - https://youtu.be/94RC-DsGMLo
- 떡=나무
- 시작점=땅과 나무의 경계
- 중간점=H
- 끝점=나무의 높이
2. 파라메트릭 서치
파라메트릭 서치란? with 나무 자르기
최적화 문제를 결정 문제로 바꾸어 푸는 것이다
최적화 문제: 문제의 상황을 만족하는 특정 변수의 최솟값, 최댓값을 구하는 문제
결정 문제: '예' 혹은 '아니오'로 답할 수 있는 문제
나무 자르기는 파라메트릭 서치로 풀 수 있는 문제이다.
- 최적화 문제: M 길이의 나무를 가져갈 수 있는 최소 높이를 구하라
- 결정 문제: (특정 H 높이에 대해) M 길이의 나무를 가져갈 수 있는가, 없는가?
그렇다면, 이 결정 문제를 도대체 어떤 H에게 묻는 것이 좋을까?
아직 아무런 정보가 없으니 H 범위의 중간 값에 먼저 물어본다.
그렇다면 그 값을 기준으로 양쪽 범위 중 한 쪽은 적어도 확실히 No라는 것을 알게 될 것이다.
이런 식으로 범위를 좁혀나가 결국 답을 찾을 수 있다.
(= 이분 탐색의 원리를 적용)
이렇게 최적화 문제를 결정 문제로 바꾸는 것을 파라메트릭 서치라 하며,
이에 이분탐색의 원리를 적용하여 답을 찾아나갈 수 있다.
파라메트릭 서치의 조건
1) 결정 문제를 정의했을 때, 쉽게 풀 수 있는 경우
2) 가능한 해의 영역이 연속적이어야 한다.
3. 문제 풀이
const fs = require('fs');
const file = process.platform === 'linux' ? '/dev/stdin' : './input.txt';
const input = fs.readFileSync(file).toString().trim().split('\n');
const [N, M] = input.shift().split(' ').map(Number);
const trees = input[0].split(' ').map(Number);
const binarySearch = () => {
let start = 0;
let end = Math.max(...trees); // 1,000,000,000으로 해도 됨(나무 높이 최댓값)
let middle = Math.floor((start + end) / 2);
let H = middle; // (1)
let sum = 0;
while (start <= end) {
sum = 0;
// forEach로 하면 400ms 정도 느려짐
for (let tree of trees) {
if (tree > middle) {
sum += tree - middle;
}
}
if (sum === M) return middle; // (2)
if (sum > M) {
start = middle + 1;
H = middle; // 가능성이 있는 값 저장
middle = Math.floor((start + end) / 2);
} else {
end = middle - 1;
middle = start + Math.floor((end - start) / 2);
}
}
return H;
};
console.log(binarySearch());(1)의 H가 필요한 이유
최적해가 소수점일 수 있지만 문제에서 정수값을 요구하기 때문에 최적해에 가장 가까운 정수값을 찾아야 한다.
따라서 일반적인 이분 탐색과 달리 (2)에서 무조건 답이 나온다고 할 수 없다.
3. 파라메트릭 서치 문제 추천
- 1654번: 랜선 자르기 - 실버 3, 나무 자르기랑 비슷해보이지만 다르게 풀어야 해서 연습해보기 좋을 듯
- 2512번: 예산 - 실버 3, 연습문제 하나 더
- 2470번: 두 용액 - 골드 5, 이제 난이도 있는 것도 풀어보시오
- 2613번: 숫자구슬 - 골드 2, 이제 더 어려운 것도!
