[Algorithm] Dynamic Programming

Preface

이번 글에서는 동적프로그래밍의 문제 해결 프레임에 초점을 맞추었다. 자잘한 부분보다는 문제해결의 핵심인 프레임에 중점을 맞추면 dp 해결에 한걸음 다가설 수 있다.

동적 계획법의 해결 방법

DP의 일반적인 형식은 최댓값을 구하는 것이다. 예를 들어 최장 증가 부분 수열(Longest increasing subsequence)와 최소 편집 거리(minimum edit distance)등을 구하는데 사용된다.

그렇다면 최댓값 구하기에서 핵심은 무엇일까?
기본적으로는 무차별 탐색(brute force) 이다. 최댓값 구하기는 가능한 모든 답을 탐색한 뒤 그 중에서 최댓값을 반환하는 것이기 때문이다.
따라서, 최댓값 구하기 => 무차별 탐색을 반사적으로 떠올리자!!

하지만 무차별 탐색은 그리 간단하지 않다. 동적계획법의 무차별 탐색이 특별한 이유는, 이 문제의 유형이 하위 중첩 문제가 있기 때문이다..!
무차별 탐색 그 자체는 효율이 매우 낮아 불필요한 계산을 피하기 위해서는 Memo(메모) 또는 DP 테이블을 사용한 최적화가 필수이다.

이러한 최적화를 통하여 DP는 최적의 하위 구조를 가질 수 있으며, 하위문제의 최댓값으로 상위 문제의 최댓값을 구할 수 있다.

DP의 3가지 요소

앞서 언급한

1. 하위 중첩 문제
2. 최적 하위 구조
3. 상태 전이 방정식

은 DP의 3가지 요소이다.

이 셋중 3.상태 전이 방정식을 작성하는 것이 가장 난이도가 높다고 할 수 있다. 이를 위해서는 4가지를 고려해야 한다.

<상태 전이 방정식을 위해 고려해야 될 4단계 >

1. 이 문제의 base case(가장 간단한 상황)는 무엇인가?
2. 이 문제는 어떤 "상태(state)" 를 가지고 있는가?
3. 각 "상태"는 어떤 "선택"을 통해 변화시킬 수 있는가?
4. 어떻게 DP 배열과 함수를 정의해 "상태"와 "선택"을 표현하는가?

다음은 위에 대한 코드 프레임이다.

dp[0][0][...] = base case

//상태 전이 방정식
for 상태1 in 상태1의 모든 데이터:
	for 상태2 in 상태2의 모든 데이터:
    	for..
        	dp[상태1][상태2][...] = 최댓값 구하기(선택1, 선택2)

이제 피보나치 수열 문제와 동전 계산하기 문제를 통해 DP의 기본 원리를 설명한다. 피보나치수열에 대해서는 중첩 하위 문제를 설명, 동전 계산하기는 상태 전이 방정식의 설명에 초점을 맞출 것이다 .

피보나치 수열

간단한 문제를 통해 설명하면 알고리즘 아이디어와 기법에 집중하게 하고 혼동을 일으키지 않으므로 다음의 예를 확인한다 .

무차별 재귀

int fib(int N){
	if (N==0) return 0;
    if (N==1 ||| N==2) return 1;
    return fib(N-1) + fib(N-2);
}

이 방식의 코드는 이해가 쉽지만 비효율적이다. N=6일때 재귀트리를 그려본다.

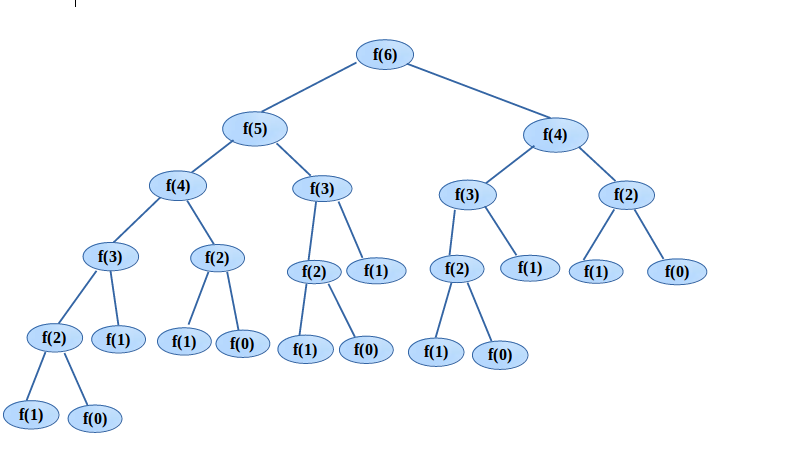
이 재귀 트리의 의미는 무엇일까?
원래 문제 f(6)을 계산하려면 먼저 f(5) 와 f(4)의 문제를 계산해야 하고, f(5)를 계산하려면 f(4)와 f(3)을 계산해야 한다. 이와 같이 계속 진행하다가 f(0)또는 f(1)을 만나면 결과를 직접 반환하며 재귀 트리는 더이상 아래로 뻗어나가지 않는다.

재귀 알고리즘의 시간 복잡도는 어떻게 계산하는가? 하위 문제 개수에 하위 문제 하나를 해결하는 데 걸리는 시간을 계산하면 된다.
먼저 하위 문제의 개수, 즉, 재귀 트리의 총 노드수를 계산한다. 이진트리 노드의 총 개수는 지수로 나타내며 $O(2^n)$ 이다.

그 다음 하위 문제 하나를 해결하는 데 걸리는 시간을 계산 한다. 이 알고리즘은 루프가 없고 f(n-1)+f(n-2)덧셈 계산 뿐이므로 시간 복잡도는 O(1)이다.

따라서 알고리즘의 시간 복잡도는 둘의 곱인 $O(2^n)$이다.
이는 상당히 비효율적이다.

이것이 DP의 첫번째 속성인 하위 중첩 문제이다. 이를 해결해보자.

메모를 사용하는 재귀 해결 방법 (하향식, Top Down)

문제는 명확해졌다. 중복으로 인해 계산시간이 오래 걸리므로
1. 메모를 만들고
2. 계산마다 하위 문제의 답을 계산해
3. 메모에 기록한뒤 반환한다.

일반적으로 배열을 메모로 활용한다.

class Fibonacci{
	static int fib(int N){
    	if(N==0) return 0;
        //메모를 모두 0으로 초기화
        int memo[] = new int [N+1];
        Arrays.fill(memo,0);
        //메모를 갖는 재귀
        return helper(memo,N);
    }
    static int helper(memo[], int n){
    	//base case
        if(n==1 || n==2) return 1;
        //이미 계산한 부분
        if(memo[n] !=0) return memo[n];
        memo[n] = helper(memo,n-1)+ helper(memo,n-2);
        return memo[n];
    }
    
}

메모를 가진 재귀 알고리즘은 가지치기를 통해 중복이 없는 재귀 그래프로 변환하는 것으로 하위문제 수를 크게 줄인다.

이 알고리즘은 중복 계산이 없으므로 하위 문제수와 입력 크기 N=20에 비례하므로 Time Complexity는 O(n) 이다.

DP배열을 이용한 반복 해법 (Bottom-Up, 상향식)

이 방식은 앞서 만든 메모를 더 발전 시킨 케이스이다.
이를 DP테이블이라고 하며, 이 테이블에서 상향식 계산을 깔끔하게 처리한다.

int fib(int N){
	if(N==0) return 0;
    if(N==1||N==2) return 1;
    
    int dp[] = new int[N+1];
    Arrays.fill(dp,0);
    //base case
    dp[1]=dp[2]=1;
    for(int i=0; i<dp.length;i++){
    	dp[i]= dp[i-1]+dp[i-2];
    }
    return dp[N];
}

위의 코드를 아래의 그림과 같이 시각화 할 수 있다.

오른쪽으로 갈수록 상향식인 것이다.

DP에서 가장 어려운 부분은 무차별 탐색, 즉, 상태전이 방정식을 사용하기 때문에 무차별 탐색을 가볍게 여기면 안된다. 무차별 탐색을 사용한 최적화는 dp table 혹은 메모를 사용하는 것에 지나지 않는다...!

사실 피보나치는 앞선 두가지의 상태와 관련이 있다는 점만 알면 다음과 같은 코드도 가능하다.

int fib(int N){
	if(N==0) return 0;
    if(N==1||N==2) return 1;
    int prev=1, curr=1;
    for(int i=3;i<=N; i++){
    	int sum = prev+curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

위와 같은 코드는 고정된 변수만 사용하므로 O(1)의 공간복잡도를 자랑한다.
너무 긴 dp테이블을 저장할 필요가 없다!

이 기법을 "상태압축" 이라고 한다. 각 상태전이에서 DP테이블의 일부분만 필요하다는 것을 깨달으면 상태압축을 통해 DP테이블의 크기를 줄이고 필요한 데이터만 기록할 수 있다.

느낀점😀

DP의 핵심은 상태전이 방정식, 즉, 결국 무차별 탐색에 바탕을 두고 있으며 dp table과 memo를 활용해 bottom up 또는 top down 방식으로 최적화를할 수 있음을 정리하는데 큰 도움이 되었다.

상태전이 방정식을 찾는 것은 꾸준한 문제풀이를 통한 훈련이 필요할 것 같다. ❤