17강 적률생성함수

해당 내용은 아래 강좌를 정리한 내용입니다.
https://www.edwith.org/ai152

학습목표

무기억성이 있는 연속확률변수는 지수분포를 따름을 이해한다. 적률생성함수를 이해하고 활용할 수 있다. 라플라스의 후속확률을 이해할 수 있다.

핵심키워드

• 무기억성
• 적률생성함수
• 적률
• 라플라스의 후속 규칙
• 사전확률, 사후확률

적률 생성 함수 (Moment Generating Function) MGF

MGF는 PDF나 CDF처럼 분포를 설명하는 방법 중 하나임.

MGF $M(t)=E(e^{tX})$

여기서 선형성에 의해 E가 들어갈 수 있게 되고(사실 좀 더 엄밀한 증명이 필요하다고 함) E(X^n)이 n차 적률인데, 모든 적률을 다 포함하고 있어서 적률생성함수라고 함.

• 테일러 전개

  함수 f를 급수 형태로 전개하는 것

  전제 : 어떤 함수 f(x)를 어떤 상황 속에서 급수 형태로 전개할 수 있는가?

  f가 무한번 미분 가능한 함수일 때

  

  $Let~ f(x) =e^x \\ e^x=\sum_0^\infin\frac{x^n}{n!}\\ e^{kx}=\sum_0^\infin\frac{k^nx^n}{n!}$

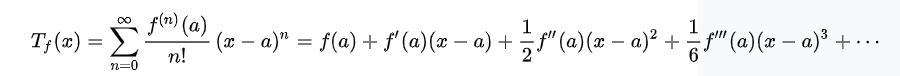
MGF가 중요한 이유

1. 적률을 구할 수 있기 때문

   $Let~X ~have ~MGF~M(t) \\ (1) ~The ~nth ~moment,~E(X^n) =M^{(n)}(t)~ then ~ t=0,$

2. MGF가 분포를 결정하기 때문 (증명하긴 어려움)

3. 만약 독립적인 두 확률변수에 대해 다음과 같은 정리를 사용할 수 있음.

   

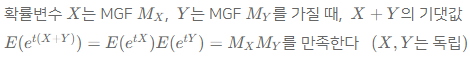
Example about distribution’s MGF

베르누이의 MGF

이항분포의 MGF (MGF 가 중요한 이유 3번 이용)

이항분포는 베르누이가 n번 일어난 것이므로 다음과 같이 쓸 수 있다.

여기서 1차 적률을 구하는 법은 미분 후 t=0 대입.

정규분포의 MGF

라플라스의 후속 규칙(Laplace’s Rule of Succession)

n일 동안 관찰했는데 n일 동안 연속으로 해가 떴을 때, 내일 해가 뜰 확률

이때 i.i.d , Bern(p)라고 전제함.

베이지안은 모수를 추정할 수 있다고 봄. 즉, p는 확률변수임.

• 베이지안과 빈도의 차이

  빈도는 모수(우리가 알아내고자 하는 평균, 분산 등)이 고정된 상수라고 해석하고 베이지안은 모수는 어떤 분포를 따르고 확률적으로 변하는 수 라고 생각함(확률변수)
  즉 베이지안은 모수를 여러 증거들로 추정함.
  

---

문제 설정은 다음과 같다. 해설해보자면

$X_n$ : n 번째 관찰한 날에 해가 뜨는 사건. 뜨면 1
$S_n$ : n 번째 날까지 관찰했는데 몇 번 해가 떴는가? , 이항분포를 따른다고 보면 됨.
p : 해가 뜰 확률 (사전확률로서 맨 처음에는 균등분포를 따른다고 가정하고 시작)
$p|S_n$ : 여태 해가 뜬 날들을 관찰한 정보들을 가진 p의 분포 (사후확률)

1. p는 확률 변수 이므로 확률밀도함수를 가짐, 이때 정보를 활용해서 조건부 확률밀도 함수를 구함. 확률밀도함수에 작은 증분을 곱한다면 대략 그 작은 구간의 확률이 나옴.
2. 처음 식은 확률이었는데 균등분포의 pdf를 이용하기위 해서 양 변에 증분을 나누어 주었다고 생각.
3. 좌변은 p에 대한 함수이며 우변의 분모는 p에 대한 종속 함수가 아님.