2장 Markov Decision Process

해당 글은 아래 강의를 보고 정리한 내용입니다.
https://www.youtube.com/watch?v=o85AaCB5Nck&list=PLKs7xpqpX1beJ5-EOFDXTVckBQFFyTxUH

배우는 이유 : 현대에 나와 있는 모든 강화학습 이론들의 근거가 되는 내용이다.

유한 MDP 에서는 State, Action, Reward 모두 유한한 값의 숫자 원소를 가지고 있다.

MarKov property

어떤 일이 히스토리를 가져서 현재상황에 왔을 때 다음 상황은 직전 상황으로 인해서만 결정된다.
→ t 시간의 사건은 t-1, .... ,0 에 일어난 사건을 반영한 사건이다.

Markov process (MP)란?

Markov property를 가지는 이산시간 확률 과정이다.
- 확률 과정이란 시간에 따라 어떤 사건이 발생할 확률이 변하는 과정을 의미.

<참고자료>
https://bskyvision.com/573

Terminology :

• Agent : the learner and the decision maker

• Environment : the thing that an agent interacts with

• Task : a complete specification of an environment including rewards

• Return (G_t) : the total discounted reward from time t //할인율까지 고려한 총 보상 (R_t+1 + r * R_t+2 ... ) 당연히 s에 따라 R_t+2이 달라지므로 바뀜.

*참고 : t에서의 action에 대한 보상은 R_t+1임

수식 표기법 :

S = 가능한 상태 집합 (set of states) , s_t = t에서의 상태 s

P = state transition probability matrix

P_ss’ = s 에서 s’로 transition 할 확률

R = reward function

Rs = E [ R(t+1) | S_t = s] // 상태 s에서 얻을 수 있는 보상의 평균 (s’ 마다 다르기 때문에 평균을 취함)

v(s) = state - value function // state s에서 앞으로 기대할 수 있는 return의 평균 == 다음 스탭으로 나아갈 때의 근거

r = 할인율

pi (a|s) = 현재 상태 s에서 Action a를 할 확률 (정책) / 오직 현재 상태로만 결정

Markov process

Markov process를 나타내는 수식은 다음과 같다.

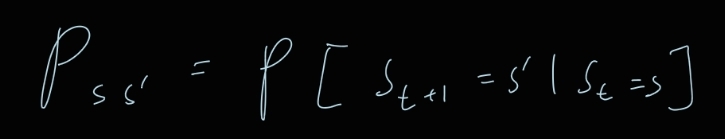
Markov Reward Process

Markov process에 reward를 추가한 개념

• 구성 요소 : < S, P, R, r >
• Bellman Equation for MRP

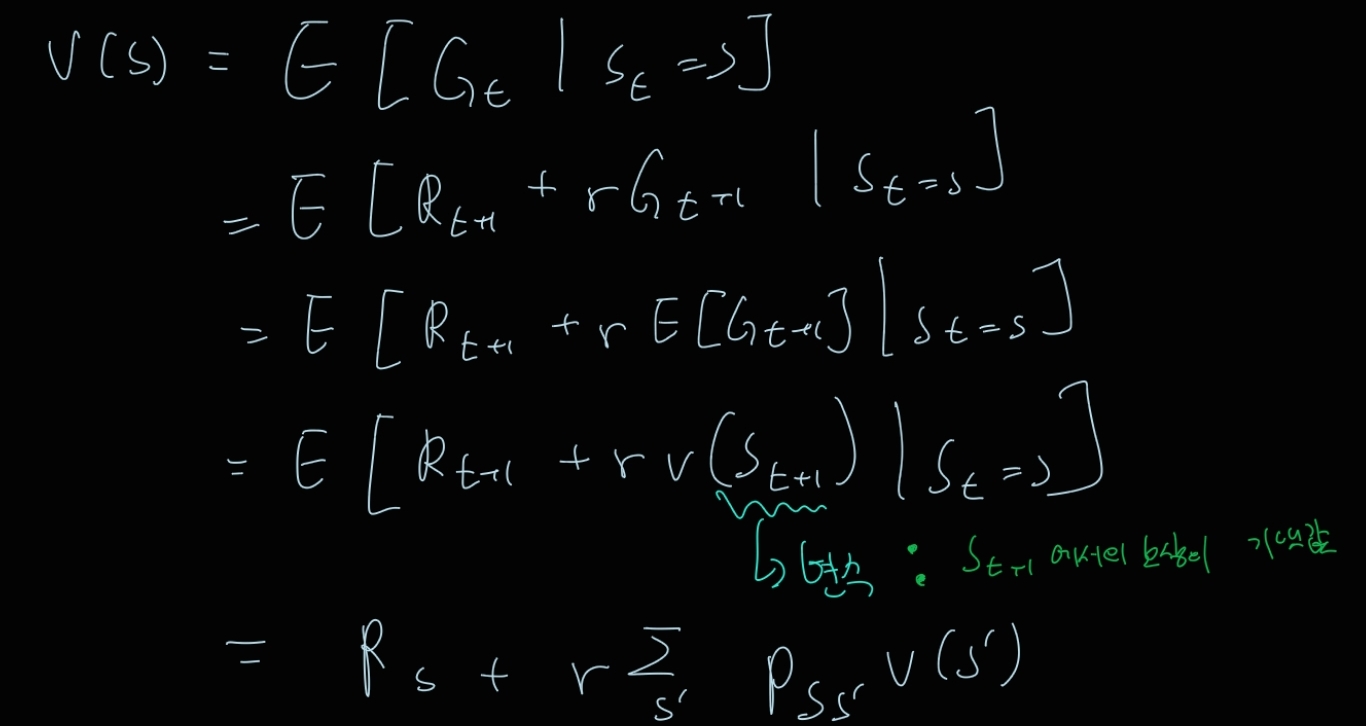
의의 : value function을 다음 상태의 value function으로 나타냄.

• Bellman Equation for MRP in Matrix Form

  v = R + rPv

  

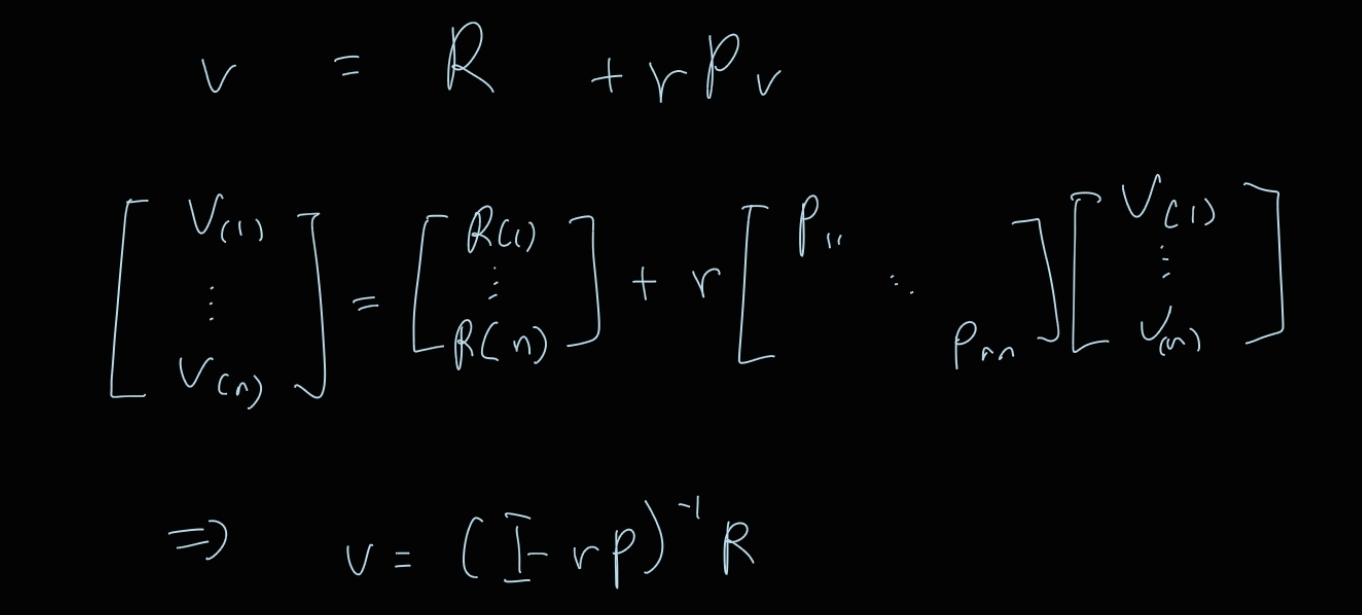
  만약 특정 장소에 가야 끝나는 경우나 시간 제약이 없는 경우 좌변의 v(1)과 우변의 v(1)은 같다.

  이렇게 행렬 form으로 나타낼 경우 O(n^3)의 시간 복잡도가 걸린다.
  

Markov Decision Process

MRP에 action이 추가된 Process

• 구성 요소 : <S, A, P, R, r>
• 강화학습에서는 Policies are time-invariant 인 문제라고 생각하고 푼다. ( 오늘의 정책 = 내일의 정책)
• MDP 를 MP로 바꾸는 법 $P_{ss'}^\pi = \sum\limits_{a}\pi(a|s)P_{ss'}^a$
  → s에서 s’으로 갈 확률은 상태 s에서 a행동을 하여 S’으로 갈 확률의 총 합
  
• MDP를 MRP로 바꾸는 법 $R_S^\pi=\sum\limits_a\pi(a|s)R_S^a$ → 상태 s에서 받을 수 있는 보상의 평균은 상태 s 에서 할 수 있는 행동 a를 해서 받는 보상의 기댓값
  

가치 함수의 정의

상태 - 가치 함수

$v_\pi(s) = E_\pi[G_t|S_t=s]$

상태 s에서 기대할 수 있는 보상의 평균

= 정책에 따라 가중평균이 됨.

행동 - 가치 함수

$q_\pi(s,a) = E_\pi[G_t|S_t=s,A_t=a]$

상태 s에서 행동 a를 취했을 때 기대할 수 있는 return의 평균

Bellman Expectation Equation은 4가지가 있다.

Bellman Expectation Equation for v, q 그리고 Bellman optimal for v, q

Bellman Expactation Equation for V

의의 : v를 v로 표현할수도 있고 q로 표현할 수도 있음

Graphical description

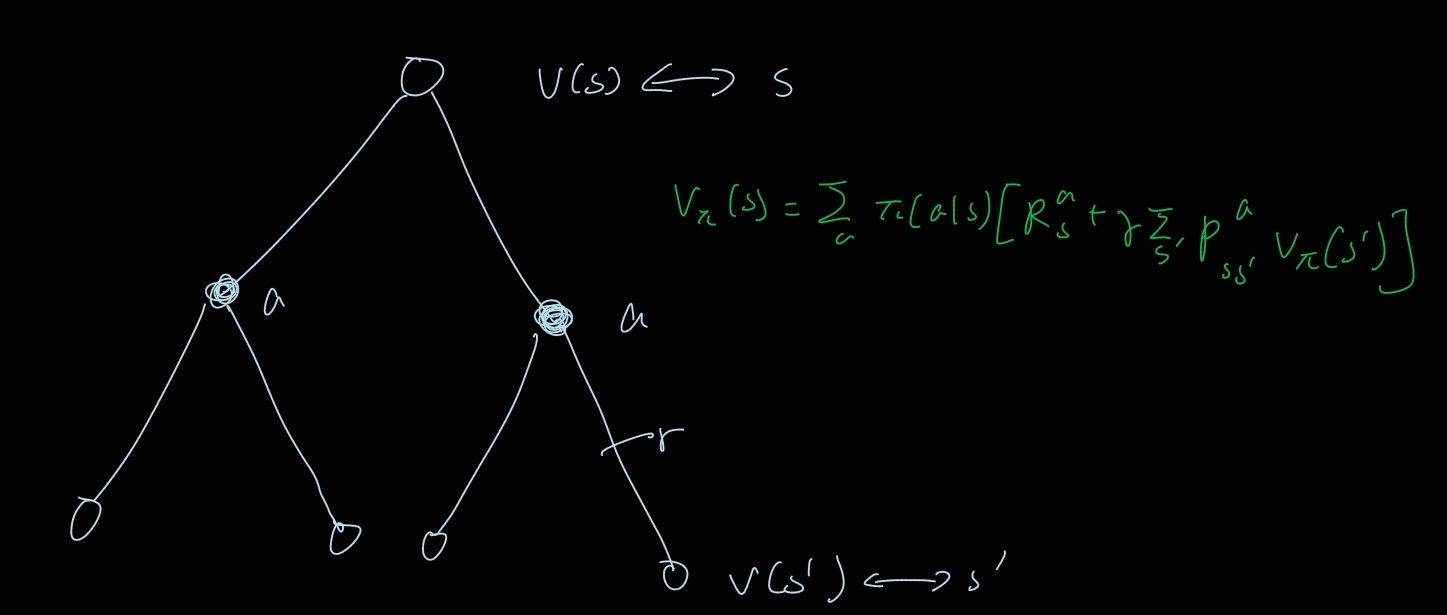
s의 value = a의 기댓값 [상태 s에서 a를 취했을 때의 이득평균 + a를 취할 확률 s’에서의 value]

이 그림에서 a를 취했을 때 상태가 2개가 되나? a당 하나여야 하는거 아닌가? action을 취한다고 해서 상태가 무조건 변하는 건 아니니까 다음과 같이 표현할 수 있긴 할듯. 만약 하나의 상태가 된다면 한쪽 엣지의 확률을 0으로 주면 될 거 같다.

Graphical description v → q

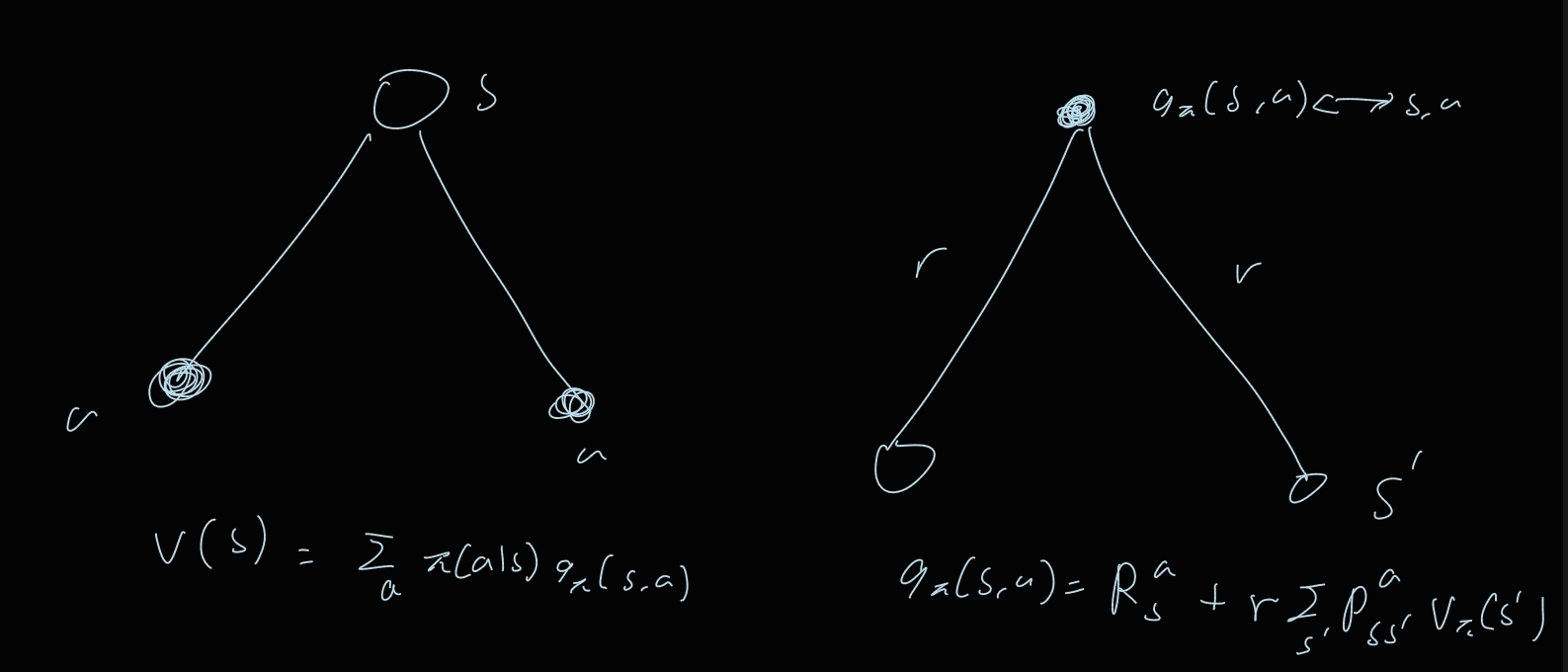
$P^a_{ss'}$ : 상태 s에서 a를 취했을 때 상태 s’이 될 확률

참고로 오른쪽 그림에서 현재 상태는 s임.

시그마에 s’이 있는건 보상의 평균을 구하기 위해서는 모든 s’을 구해야하기 때문.

Bellman Expactation Equation for q

의의 : q를 q로 표현할 수도 있고 v로 표현할 수도 있음.

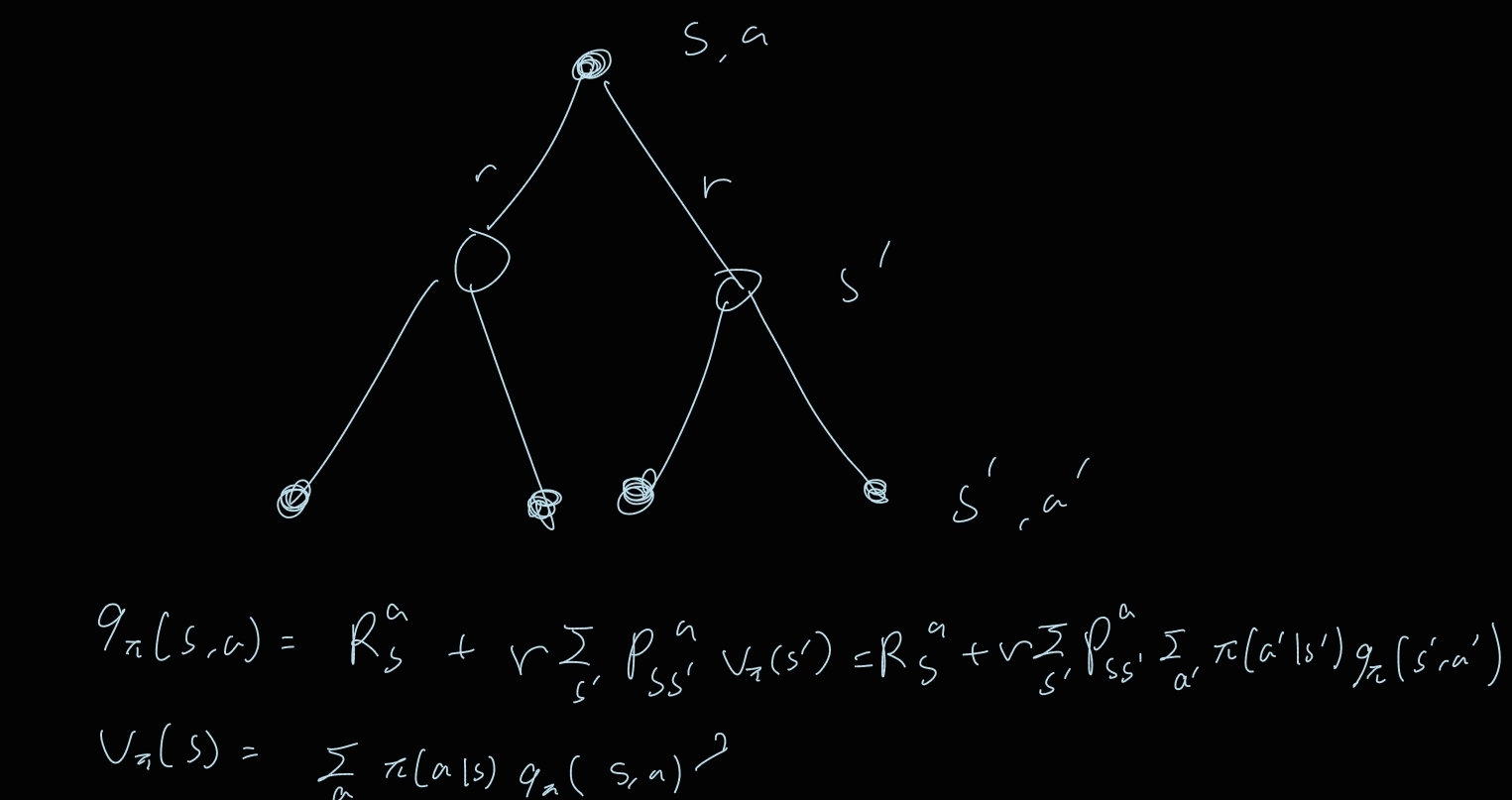
Bellman Expectation Equation을 이용하여 무엇을 할 수 있는가?

모든 s 마다 행렬로 나타내어 보자

$v_\pi(s)=\sum\limits_a\pi(a|s)[R_s^a+\gamma\sum\limits_{s'}v_{pi}(s')] \\->\\v_\pi=R^\pi+\gamma P^\pi v_\pi\\=>\\ v_\pi=(I-\gamma P^\pi)^{-1}R^\pi$

다음과 같이 식을 전개하면 역행렬을 구하여 가치 함수를 찾아낼 수 있음.

근데 이 것의 전제 조건은 R과 P의 값을 알아야 하는 것인데, 이는 모델을 완벽히 알고 있을 때에만 가능함.

$R^\pi$ : 보상을 a로 평균을 취한 것, 즉 (s,1)

$P^\pi$ : matrix 자체를 a에 대해서 평균을 취한 것임, 즉 (s,s)

다만 위와 같은 경우에도 시간 복잡도가 O(n^3)으로 크기 때문에 좀 더 최적화가 필요함.

Optimal Value Function

정의 : 모든 가능한 정책 중에서 보상을 최대로 하는 정책(optimal policy)을 했을 때의 value function

• optimal policy의 정의 및 성질
  $\pi \geq \pi^\prime \;\; if \;v_\pi(s) > v_{\pi^\prime}(s),\; \forall s$
  모든 상태 s에 대해 정책 pi가 더 큰 가치함수를 만든다면 다음과 같이 표시한다. 이때 가장 큰 pi를 optimal policy라고 한다. optimal policy의 성질 $v_*(s)=max_\pi v_\pi(s)$ $q_*(s,a)=max_\pi q_\pi(s,a)$ optimal policy의 존재 가능성 정책이란 상태 s에서 행동 a를 할 확률이다. 즉, 상태와 행동이 변수가 된다. 만약 상태 1에선 정책 1이 좋고 상태 2에선 정책 2가 좋다고 하자. 그렇다면 상태 1에선 정책 1을 따르고 상태 2에선 정책 2를 따르는 정책을 만들면 됨.
  

optimal policy의 존재는 deterministic optimal policy의 존재를 말함.

즉, 다시 말해 stochastic(확률적)이지 않고 결정론적으로 행동을 결정할 수 있다는 뜻.

deterministic의 중요한 점은 unique한 건 보장되지 않기 때문이다.

가장 큰 value function을 만드는 방법

$v_\pi =\sum\limits_a\pi(a|s)q(s,a)$ 의 의미는 상태 s에서 행동 a를 취했을 때 얻을 수 있는 return의 평균임. 즉, a마다 q(s,a)가 다르고 이의 평균을 계산한 것인데, 최댓값의 확률을 1로 놓는게 가장 큰 보상을 만드는 것임. 예를 들어, a1의 보상 3 확률 0.3, a2의 보상 100 확률 0.7 이면 a2를 할 확률을 1으로 만드는게 더 높은 보상이 됨.

참고로 이때 가장 큰 보상이 만들어졌으므로 a2를 할 확률 1인 정책(deterministic)이 optimal policy가 됨.

식으로 value function을 표현하면 $v_*(s) = \max\limits_aq(s,a)$ 으로 쓸 수 있음.

식으로 q function을 표현하면

*근데 여기서 정책이 바뀌면 q(s,a)가 바뀌지 않나...?

Bellman Optimality Equation 은 Expactation Equation과는 달리 개념적으로도 답을 구할 수 없다.

왜냐하면 non-linear하기 때문에 (max함수가 들어감) .

연속적인 값에서의 MDP는 quantization을 이용하여 구간을 나누어 대표값을 선정한 후 이산적 MDP를 풀 수 있음.

POMDP 등등은 우선 넘어감.