경사하강법은 3가지 종류로 구분된다.

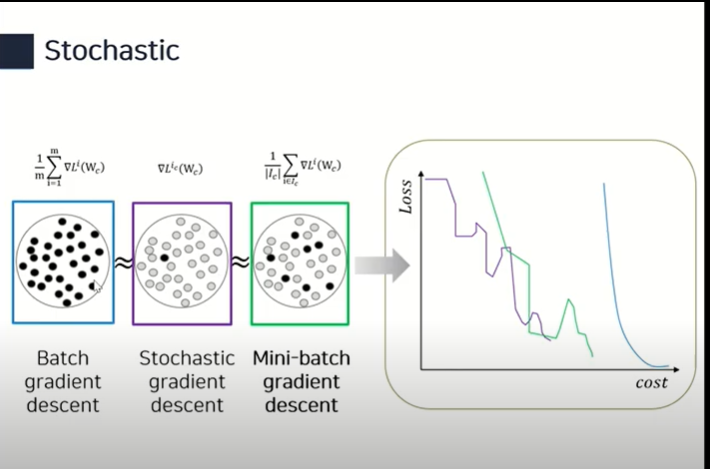
위 수식에서 볼 수 있듯 파라미터 최적화 과정은 오차함수의 평균 기울기로 계산한다.

사진 출처
https://www.youtube.com/watch?v=8NeD-B5e32M

1. Stochastic gradient descent
   Update with the gradient computed from a single sample
   (전체 데이터 중 하나를 랜덤으로 가져와서 최적화를 진행한다.)

2. Mini-batch gradient descent
   Update with the gradient computed from a subset of data (batch size)
   (전체 데이터 중 일부를 가져와서 최적화를 진행한다.)

3. Batch gradient descent
   Update with the gradient computed from the whole data
   (전체 데이터를 대상으로 하기 때문에 각각의 오차함수를 더하고 그걸 가중치로 미분하려면 계산량이 많다.)

각각 수식으로 어떻게 다른지 이해하기 위해 참고하면 좋을 영상
https://www.youtube.com/watch?v=gHcu0NKyli4

Gradient Descents 파라미터 최적화 방법들

여기서 eta는 learning rate로 사용한다.

1. (Stochastic) Gradient descent

단점 : learning rate 잡기가 힘듦

2. Momentum

알파를 이용해서 이전 mini batch에서의 정보를 버리지 않고 현재 gradient값과 더해서 accumulation을 만들어낸 다음 그걸 학습에 사용


$\beta$ : momentum
$a$ : accumulation

이 방법을 사용하면 gradient가 왔다갔다 하는 경우도 잘 학습이 된다.
즉, local minima 문제에 도움이 된다.

3. Nesterov Accelerated Gradient (NAG)

$\nabla \mathcal{L}(W_t -\eta \beta a_{t})$ : Lookahead gradient

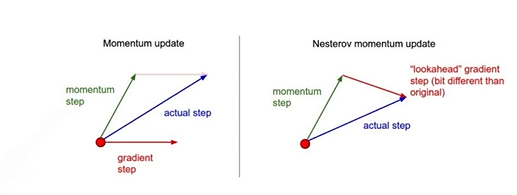
위에서 Momentum 방식에서는 accumulation을 현재 gradient $g_t$를 이용해서 계산했다면, NAG는 현재 $a_t$를 이용하여 가보고 그걸 토대로 그 위치에서의 gradient를 계산함

나중에 추가로 공부해야 함!

4. Adagrad (Adaptive Gradient)

Adagrad adapts the learning rate, performing larger updates for infrequent and smaller updates for frequent parameters.
-> 파라미터 별로 stepsize를 다르게 적용하기 때문에 파라미터 별 여태까지의 변화 정보 저장 필요 -> $G_t$ 에 저장

$G_t$ : Sum of gradient squares (지금까지 gradient가 얼마나 변했는지를 제곱해서 더함)

$\epsilon$ : for numerical stability (0으로 나누는거 방지)

단점 : $G_t$는 계속 증가하기 때문에 나중엔 parameter 최적화가 안됨

5.Adadelta

Adadelta extends Adagrad to reduce its monotonically decreasing the learning rate by restricting the accumulation window.

* 지수이동평균이란?

과거의 모든 대상의 정보를 포함하면서 현재의 정보에 가중치를 줄 수 있는 방법
$\gamma$가 0~1 사이의 값으로 과거 정보에 대한 영향력을 의미하며 $(1-\gamma)g_t^2$은 새로 들어오는 정보의 특징을 의미함.

$G_t$ : EMA of gradient squares
$H_t$ : EMA of difference squares (변화시키려는 weight의 변화값)
learning rate가 없다는게 특징

$H_t$ 가 어떻게 stopsize를 대체할 수 있을까?

• 추가적인 공부 필요

6. RMSprop

RMSprop is an unpublished, adaptive learning rate method proposed by Geoff Hinton in his lecture.

$G_t$ : EMA of gradient squares

7. Adam (Adaptive Moment Estimation)

Adaptive Moment Estimation (Adam) leverages both path gradients and squared gradients.

gradient와 momentum 방식을 모두 사용한 방식
$\beta_1$은 이전 momentum과 현재 gradient 중 어느 것에 초점을 맞출 지 결정하는 역할을 한다.

$m_t$ : Momentum
$v_t$ : EMA of gradient squares

추후 공부 예정