이 글은 아래 강의를 참고하여 쓴 글입니다.
- 강화학습 7강

이전까지 가치 기반 방법들의 경우는 v 함수, (state value function)과 q 함수 (action value function)을 추정하여 문제를 풀었다.

일반적으로 model free 환경의 경우 우리는 상태 변환 확률을 모르고 있으므로 상태 가치 함수를 이용하긴 힘들다.

따라서 q 함수를 이용하게 되는데, 이때 agent의 행동을 결정하는 방법으로는 해당 state에서의 가장 높은 a를 선택하는 것이다.

하지만 이번에는 정책을 추정하여 행동을 하는 방법인 Policy Gradient 방법을 배운다.

Policy Gradient

장점

• 정책 추정에서의 수렴성이 좋다.
• continuous action spaces의 경우 q 함수 추정이 힘든 반면, 이 방법은 비교적 효과적이다.
• stochastic한 policies를 학습할 수 있다.
  • 여태까지의 value based 방법에서는 greedy하게 action을 선택했다.
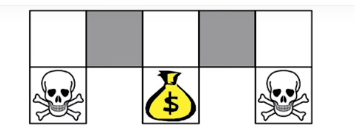
  • state를 모델링했는데, 구분이 안될 때(partially observeble) 결정적인 policy를 취하는 건 위험할 수 있다. (회색 칸 구분 x)
    

단점

• local minimum 문제에 잘 빠지는 경향이 있다.

Policy Objective Functions (maximization)

Policy를 학습시키기 위해서는 적절한 목적함수가 필요하다.

위 강의에서 목적함수는 세 개를 소개해주신다.

1. episodic
   $J(\theta)=V^{\pi_\theta}(s_1)=E_{\pi_\theta} [v_1]$

• 끝이 있는 경우이므로 시작으로부터 정책을 따랐을 때 얻을 수 있는 보상의 기댓값 최대화를 의미

2. continuing environments

$d^{\pi_\theta}(s)$ : 임의의 시간에서 정책을 따랐을 때, 각 상태에 있을 확률

여기서 이 문제는 markov chain의 정상 상태에 도달했다고 가정한다.

위 식도 직관적으로 해당 정책이 주는 보상을 전체 state의 value의 기댓값으로 평가한다.

3. reward per time-step

위 식은 2번과 비슷한 개념인데 이를 한 스탭만 생각하여 계산한 것이다. (임의의 시점에 각 상태에 있을 확률은 수렴했다고 보기 때문에)

Gradient의 계산

위에서 정의한 목적함수를 최적화 하기 위해서 우리는 $\nabla_\theta J(\theta)$를 계산해야 한다.

하지만 이를 직접 계산하기는 굉장히 어렵다고 한다.

그래서 다음과 같은 방법을 사용하여 gradient 계산을 편하게 할 수 있다.

Likelihood ratio

log x의 미분이 1/x라는 것을 이용하여 그라디어트를 다음과 같이 변형했다.
이때, $\nabla_\theta log\pi_\theta(s,a)$는 score function이라고 한다.

여기서 이러한 행동을 하는 이유는 정책이자 확률값인 $\pi_\theta(s,a)$ 를 앞으로 빼내기 위함이다.

이 방법을 이용하여 One-Step MDP 문제의 gradient를 계산해보자.

One-Step이란 한번 이동하고 끝나는 문제이다.

이떄, 처음 상태는 정책과 관련없이 분포한다는 것을 기억하자.

위에서 본 Likelihood ratio 방법을 통해 빼낸 정책으로 기댓값을 만들어서 다음과 같이 그레디언트 값을 score function과 보상값의 곱으로 계산할 수 있다.

우리가 적절한 $\pi_\theta$ 를 정의한다면, 이를 쉽게 $\theta$에 대해 미분하여 gradient 값을 계산할 수 있다.

예를 들어, softmax policy가 있겠다.

Policy Gradint Theorem

이 Theorem은 위와 같은 one step MDP에서 multi step MDP에서도 적용된다. 그리고 one step MDP에서는 3번째 목적함수를 가져왔는데, 이 식을 이용하면 세 가지 목적함수를 모두 최적화한다고 한다.

$\nabla_\theta J(\theta) = \ E_{\pi_\theta}[\nabla_\theta log \pi_\theta(s,a) \ Q^{\pi_\theta}(s,a)]$

엄밀한 증명을 건너뛰고 이 식을 직관적을 이해해보자면, one step에서의 r이 s에서 a라는 행동을 했을 때 얻는 총 보상이라고 수 있다.

하지만 multi-step에서는 r뿐만 아니라 이후에 얻는 보상들도 더해줘야 한다.

이때 q함수의 정의가 s에서 a라는 행동을 했을 때 앞으로 얻는 총 보상의 합임을 생각해보면 어느 정도 납득 가능하다.

결국 정리해보자면 gradient 값은 score function와 앞으로 얻을 총 보상의 곱이다.

Reinforce

이 알고리즘은 Policy Gradient Theorem과 Monte-Carlo를 이용한 방법이다.

강화학습에서 굉장히 자주 쓰이는 기술을 여기에서도 사용했다.

수도 코드를 보면 score와 곱해지는 Q(s,a)를 알 수 없으니, 진짜 시뮬레이션을 하고 난 이후의 return값인 G_t (여기서는 v_t)를 사용하여 Policy Gradient Theorem을 적용했다.

Reinforce 알고리즘의 단점

기본적으로 MC를 쓰는 알고리즘이다 보니 에피소드마다 분산이 굉장히 높다.

이런 높은 분산은 학습이 굉장히 오래 걸리게 만든다.

이후에는 분산을 줄이기 위해 Critic을 이용하게 된다.

Reducing Variance Using a Critic

Reinforce 방법에서는 score와 곱해지는 Q(s,a)를 알 수 없어서 MC의 결과값인 return 값을 이용했는데, 높은 분산값을 가지는 MC의 return이 문제가 되었다.

그래서 MC의 return값을 사용하지 말고,

Q(s,a)를 학습해서 넣자는게 Actor-Critic의 아이디어이다.

이때, Actor는 정책을 학습, Critic은 Q함수를 학습한다.

따라서 이 방법은 정책 뿐만 아니라 행동 가치 함수인 Q 함수도 학습해야 한다.

Actor-Critic algorithm

$\delta$ : TD error
$\alpha, \beta$ : learning rate

여기서 w는 q함수에 관한 파라미터이다.

q함수를 업데이트하는 과정은 Loss를 MSE로 정의하여 계산했기 떄문에, learning rate x TD error x (w에 대한 미분값)이 된다.

전체적인 과정은 policy iteration과 굉장히 유사하게, 현재 정책을 기반으로 행동을 해보고, 그걸 기반으로 정책을 업데이트하고, q 함수를 업데이트 하는 것의 반복이다.