5. 선형변환 with Neural Networks

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자

핵심

• 선형변환의 정의
• 모든 선형변환은 행렬로 나타낼 수 있음
• Affine -> Linear는 m -> n 차원 변환을 m+1 -> n차원 변환으로 바꾸면 됨
• 변환 행렬 A에서 각각의 열벡터들은 단위기저벡터가 결과에 미치는 영향!!

Linear Transformation

Definition : A transformation (or mapping) T is linear if:

$T(c\bold u + d\bold v) = cT(\bold u) + dT(\bold v)$
for all u,v in the domain of T and for all scalars c and d

T(x) = 3x + 2 라는 변환은 위 성질을 만족을 못시키기 때문에 선형변환이 아니다.
위 변환은 $T:\R^1 \rightarrow \R^1$ 이다.

그런데 이를 다음과 같이 바꾸면 선형변환이 된다.

선형변환은 항상 행렬곱으로 나타낼 수 있다.

let T : $\R^n \rightarrow \R^m$ 이라 하자.

따라서 우린 T 변환에 기저 벡터들의 결과값을 얻으면 T를 행렬곱으로 나타낼 수 있다.

선형변환 with Neural Networks

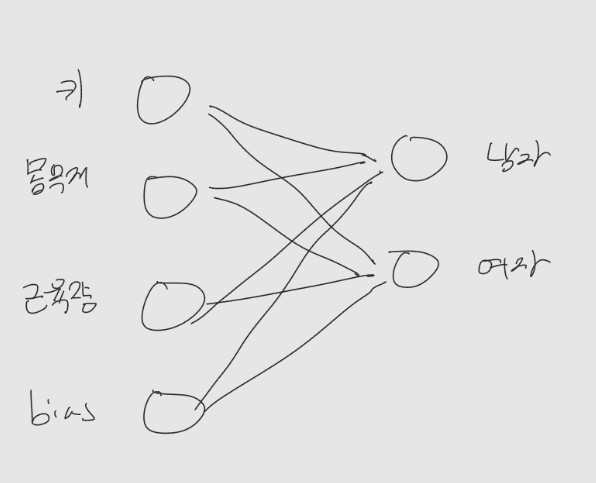
위 그림에서 확인할 수 있듯 어떤 선형변환 A에서의 열벡터는 어떠한 특성이 기여하는 정도를 나타낸다!