LEVEL :
Gold5
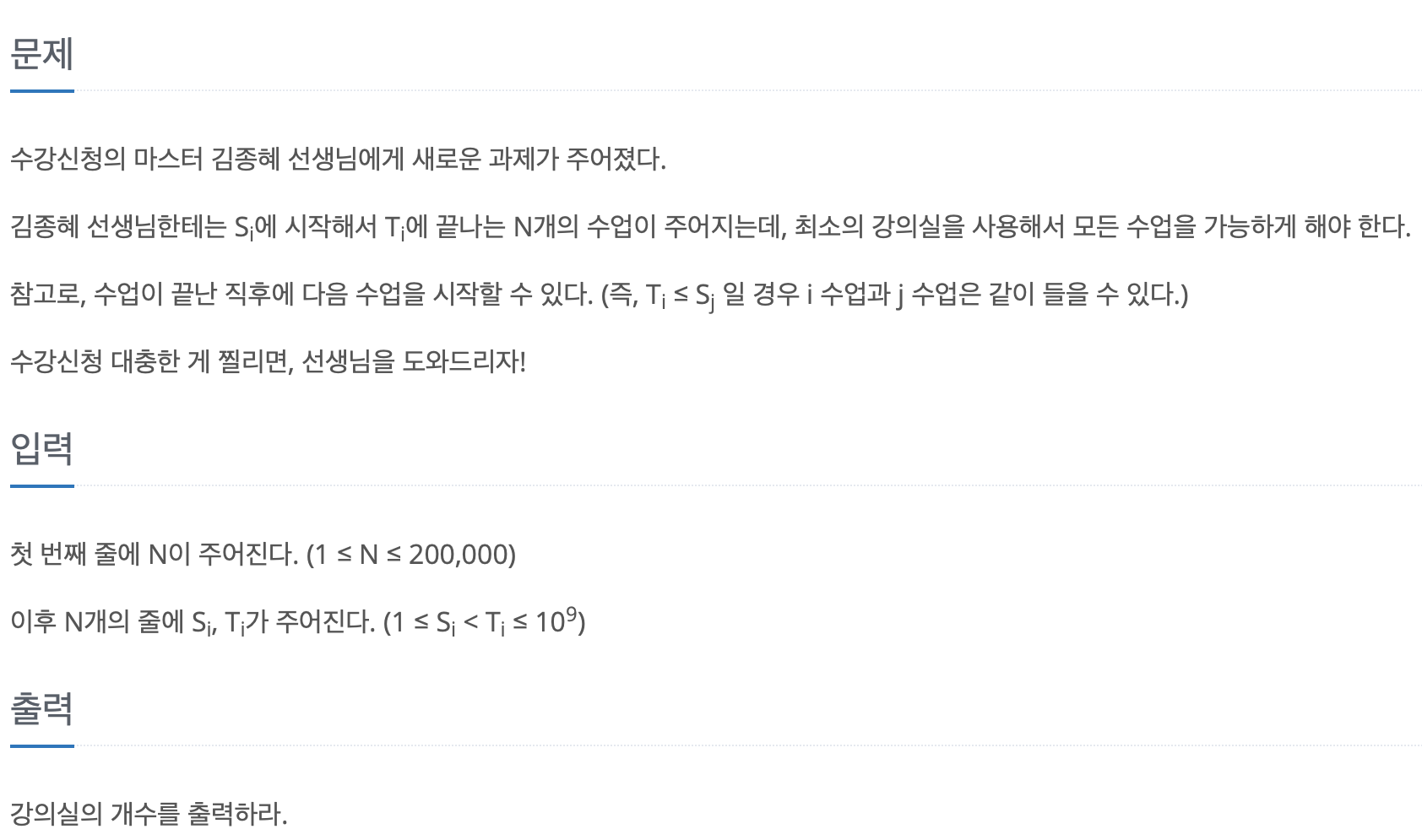
문제 요약 :
최소한의 강의실을 사용하여 모든 수업을 해야 한다.
해결 방안 :
시간 복잡도를 최소한으로 하여 문제를 해결하는 것이 관건이었다.
문제를 보자마자 가장 먼저 떠올렸던 방법은 현재 강의목록의 시작시간이 빠른 순서대로 정렬을 하여 greedy하게 알고리즘을 수행하였을 때, 놓치는 것이 없도록 하였다. 그 다음은 정렬한 수강목록을 하나씩 pop하면서 while문을 돌고 더이상 pop할 수강목록이 없을 때 까지 classroom에 geedy하게 배치해야지라고 생각했다.
현재 강의목록의 시작시간이 기존에 배치된 classroom의 끝날 시간 보다 같거나 크면 기존에 배치된 해당 classroom의 finish 값을 바꾸어 주고 위 조건을 만족하는 classroom이 없으면, new classroom을 형성해 주는 형식으로 진행하였다.
이때 강의 목록을 전부 한번씩 돌기 위한 while문의 N번 연산, 해당 강의 목록이 어떤 classroom에 속하는지 확인할 때 최악의 경우 각 강의 마다 new classroom이 필요할 수 있기에 강의 목록의 개수인 N번 비교가 필요하다 따라서 시간복잡도가 O(n^2) 이다.
결과는 당연히... 시간초과..
Solution1. -> FAIL
import sys
if __name__ == "__main__" :
n = int(input().strip())
arr = [list(map(int,input().strip().split()))for _ in range(n)]
arr.sort()
classroom = []
while(arr) :
start,finish = arr.pop(0)
if not classroom :
classroom.append([start,finish])
continue
for i in range(len(classroom)) :
if classroom[i][1] <= start :
classroom[i][1] = finish
break
else:
if i == len(classroom)-1 :
classroom.append([start,finish])
break
print(len(classroom))그렇다면? 일단 각 강의 목록을 비교하는 classroom에 넣기위해 get하는 과정인 N번의연산은 줄일 수 없다고 판단하여, 해당 강의 목록이 어떤 classroom에 속하는지 확인하기위한 비교과정의 시간복잡도를 줄여보자고 생각했다. 이를 위해 heapq 즉, 우선순위 queue라는 개념을 이용하였다.
classroom을 heapify하여 마치는 시간이 빠른 즉 마치는 시간이 제일 작은 값을 항상 0의 위치에 두는 우선순위 queue를 형성한다.
물론 push과정과,pop이후의 classroom의 heapify과정은 logN의 시간복잡도를 가진다.
결론은 classroom에 삽입시 항상 우선순위를 유지하기에 비교과정이 필요없어졌고, push과정과,pop이후의 classroom의 heapify과정의 시간복잡도만 고려해주면 된다.
Solution2. -> SUCCESS
import sys
import heapq
if __name__ == "__main__" :
n = int(input().strip())
arr = [list(map(int,input().strip().split()))for _ in range(n)]
arr = sorted(arr, key=lambda x:x[0])
classroom = []
heapq.heapify(classroom)
heapq.heappush(classroom, arr[0][1])
for i in range(1,n) :
start = arr[i][0]
finish = arr[i][1]
if classroom[0] <= start :
heapq.heappop(classroom)
heapq.heappush(classroom,finish)
else :
heapq.heappush(classroom,finish)
print(len(classroom))시간 복잡도 :
- 개별 수강목록 get을 위한 반복문 for : N번 연산
- heapq의 heapify,push를 위한 연산 : logN번의 연산
= NlogN
O(NlogN)
고찰 :
- 우선순위 큐의 개념을 다시 잡아볼 필요가 있을 듯하다.. : heapq 참고자료
- greedy 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다. 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다. 하지만 greedy 알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이다. 탐욕 알고리즘이 잘 작동하는 문제는 대부분 탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이라는 두 가지 조건이 만족된다. 탐욕스런 선택 조건은 앞의 선택이 이후의 선택에 영향을 주지 않는다는 것이며, 최적 부분 구조 조건은 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해라는 것이다. 이러한 조건이 성립하지 않는 경우에는 탐욕 알고리즘은 최적해를 구하지 못한다.
참고자료 :